燃氣熱水器熱水零等待的理論計算和優化設計

沈 威， 范峻銘， 喬 亮

（深圳市燃氣輸配及高效利用工程技術研究中心, 深圳市燃氣集團股份有限公司, 廣東 深圳 518049）

隨著人民生活水平的日益提高，居民對家庭生活熱水有了新的需求，希望能夠實現出水即熱“零等待”。對于使用普通燃氣熱水器、即熱式燃氣壁掛爐等快速燃氣熱水器的小戶型用戶，由于沒有儲熱水箱，無法直接安裝生活熱水循環系統，從而無法提供即開即用的生活熱水，這樣不僅會浪費大量的水資源，而且使用不便，這種不便對于廚房與衛生間布局間隔較遠的用戶更為明顯。目前的措施僅停留在以經驗為基礎的改善上，如在熱水管外表包裹保溫材料，或者在熱水器入水口裝設熱水微循環泵，構建生活熱水循環系統[1-6]。目前，鮮見從理論上建立燃氣熱水器點火后，相隔較遠（10 m 左右）熱水管出水溫度隨時間變化的函數。事實上，在熱水器啟動并將管里的殘余冷水排完后，熱水管出水溫度隨時間變化并不是線性的，建立熱水管出水溫度隨時間變化的函數模型，并以此為基礎進行熱水零等待、冷水零浪費優化設計，是值得探索的課題。

本文通過建立燃氣熱水器從打火點燃到穩態時浴室出水溫度隨時間變化的函數模型，計算在沒有循環泵和管道保溫材料的情況下，流水和燃氣的耗費情況，并和實際情況進行了對比。并以此為基礎，在加設保溫材料和熱水循環泵的情況下，對出水即熱時能量的節省情況進行計算分析，最后提出了解決問題的實用方案。

1 無保溫材料和循環泵情況下出水溫度隨時間變化函數的建模計算

1.1 研究對象

為簡化計算，便于建立模型，進行以下設定：燃氣熱水器安裝在廚房，出水溫度設定為48 ℃不變；浴室龍頭安裝在離廚房最遠的主臥衛生間；燃氣熱水器和浴室龍頭用一根鋼水管連接，設水管為直線型，在墻壁和地板埋設部分忽略轉彎角影響；室溫為25 ℃（298 K）不變，所有條件均在標準狀態下運行（按照國家建設部管網供水壓力服務規范要求，城市供水服務壓力為0.14 MPa）。無保溫層和循環泵時的水流向見圖1，埋在墻體或者地板中的水管橫截剖面圖見圖2，并假設：（1）無論鋼管埋設在墻體內，還是樓板內，兩側空氣溫度均為298 K。墻體和樓板的建筑材料相同，均為混凝土材質，墻體和樓板的導熱系數(ks) 均為0.79 W/(m-1·K-1)（25 ℃時的取值）；（2）墻體、樓板厚度均取0.2 m，管道埋在正中間，和兩側表面距離相等。以打開燃氣熱水器后熱水管里的冷水剛好排凈時的時間記為t=0。

圖1 無保溫層和循環泵時的水流向Fig.1 Current direction without insulation layer and circulating pump

圖2 埋在墻體中的水管橫截剖面圖Fig.2 Cross-section of water pipe buried in the wall

圖3 為微元控制容積傳熱示意圖。根據熱力學第一定律，在Δt時間內儲存在控制容積內的能量增量，必定等于進出控制容積的能量之差。本研究對象中的控制容積為圖3 中虛線所示的一段圓柱體，長dx，管道內徑為Di，管道外徑為Do。

圖3 微元控制容積傳熱示意圖Fig.3 Schematic diagram of the microelement control volume heat transfer

1.2 達到穩態時的熱傳導

達到穩態時，水管各處的水溫保持不變，對圖3中的微元控制容積進行分析，有：

適用于水管水流中微元控制容積的傳熱方程為：

寫成微分形式為：

微元控制容積從水管中向外傳遞熱量，由3 部分組成，分別是水和水管內壁的對流換熱、水管內外壁的熱傳導，水管外壁和墻壁之間的熱傳導，墻壁和空氣之間的對流換熱，則：

式中Rconv為管內水流與管壁之間的對流換熱熱阻，K/W；Rcond,i為水管的導熱熱阻，K/W；Rcond,s為從水管外管壁到墻壁表面的熱阻，K/W；Rcond,e為樓板表面與大氣的對流換熱熱阻，K/W。

于是：

假設水管埋在墻壁中間，與墻壁的兩個表面距離相等，且這個距離z遠遠大于水管半徑r，水管長度Lz，那么查表可得[8]：

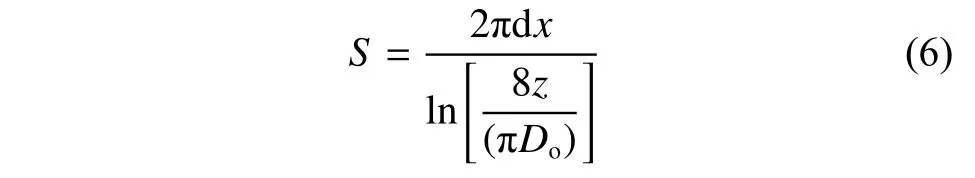
式中z為墻體中的熱水管中心軸線到墻壁之間的距離，參考值為0.1 m。

將式（6）代入式（5）可得：

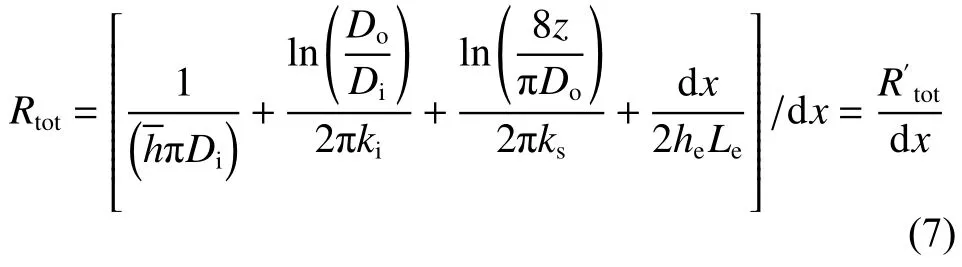
式中，由于樓板長度Le!1 ，那么可認為!0 ，式（7）簡化為：

由式（3）和式（7）可得：

燃氣熱水器熱水出口到水龍頭出水口積分可得：

為計算給定條件下的Tm,o，首先應該確定換熱系數。由于熱水器出水溫度為48 ℃，因此，取48 ℃時水的物性參數。

由雷諾公式[9]可得：

聯立式（12）和式（13）可得Re=1.19×104。

由于水的普朗特數(Pr)為3.54[7]，可以確定水管內水的流動狀態為湍流。且滿足條件Re為104～1.2×105，Pr為0.7～120，L/Di≥60，因此，對于Pr>0.6 的常規流體，可用最普遍的Dittus-Boelter 公式[7]：

式中：Nuf為努塞爾數，量綱為—。

由于流體加熱時，n=0.4；流體冷卻時，n=0.3。本文管道內的水處于冷卻狀態，因此取n=0.3。

將已知參數代入式（14），可計算得到出水管內水的努塞爾數為61.22。

根據計算式（其中k為水的導熱系數，48 ℃時參考值為0.648 W/(m·K)）：

求得h=1653 W/(m2·K) ，代入式（8）得=0.44 km/W ，代入式（11）得Tm,o=320.0 K ，即為燃氣熱水器點火后，達到穩定狀態時的出水溫度47 ℃（從理論上講，達到穩定狀態時的該溫度需要的時間為無窮大）。

調節燃氣熱水器的熱水溫度分別為45、50、55、60 ℃，同理分別計算浴室熱水管穩定狀態時的出水溫度，結果列于表1。可以看出熱水管穩定狀態時的出水溫度和熱水器的設定溫度呈線性關系。

表1 浴室熱水管出水溫度隨燃氣熱水器出水溫度的變化Table1 Outlet temperature changes of bath hot pipe with the gas water heater

由式（10）可以看出，改變積分的上限值，可以得到熱水管任意一處的水溫。管道長度x處的溫度和x呈指數關系變化，即

1.3 從熱水管中冷水排凈開始非穩態時的熱傳導

在打開燃氣熱水器后，設定熱水管里的冷水剛好排凈時為起始時間t=0，排凈冷水的時間為t0=L/ω，為了求出非穩態時出水口溫度隨時間變化的函數，引入平均溫度()的概念。

根據式（16），令a=Tm,i-Ts，b=Ts， β =，則在t時刻，沿管道長度x處的水溫可以表示為：

由已知條件：x=0 時，T(x)=321 K ，即a+b=321 ；Ts即b為 2 98 K ，那么式（18）可以寫為

代入式（17）中得：

式中 β 為時間t的函數，可以記為 β =f(t) ，或者其反函數t=f-1(β) 。

對于從燃氣熱水器出水口到浴室熱水龍頭這段水管，從打開燃氣熱水器開始直至冷水排凈，最后達到穩定態時，水管內的平均溫度不斷增加。那么取整段熱水管為控制體積，有

式（20）寫成微分形式，有

式中：T0為燃氣熱水器的設定出水溫度，T0=321 K ；TL為浴室龍頭出水溫度，TL= 2 3e-10β+298 ，K；Ts為大氣環境溫度，取值25 ℃或298 K。

代入已知數據并簡化為

其中，邊界條件由TL=23e-10β+298 來確定：

（1）t=0 時，TL=298 K ，因此 β !1 ；

（2）t!1 時，TL=320 K ， β =0.004 45 。

微分方程（22）右邊函數為非初等函數，無法以常規的方法或者數學軟件進行積分，因此考慮采用插值擬合的方法在一定區域內求近似解。將式（22）看成是t=f-10(β) 的導數，即t0==f-10(β) ，在區間[0.01，0.2]內取18 個數值，代入式（22），得到與t0相對應的18 個值。以β為橫坐標，為縱坐標，用Excel 繪制得到曲線圖（圖4），用Excel 進行曲線擬合，得到在區間[0.01,0.2]的模擬曲線方程為y=8.3241x-1.266，擬合優度為R2=0.998 1，即在此區間內，誤差小于0.2%。那么式（22）可以簡化為：

圖4 方程 的插值擬合曲線圖Fig.4 Interpolated fit plots of equation

對式（23）積分可得

由初始條件 β !1 和t=0 ，得C=0

那么此時式（24）可以表示為：

求反函數得到

代入溫度公式（19），得到燃氣熱水器設定出水溫度為48 ℃時，浴室熱水管中冷水排凈后出水溫度與時間的函數關系為

同理，計算得到當燃氣熱水器的設定出水溫度分別為45、50、55 ℃時，浴室熱水管中冷水排凈后出水溫度與時間的函數關系，分別如式（26）～式（28）所示，變化曲線圖如圖5 所示。

圖5 熱水管出水溫度隨時間變化的曲線圖Fig.5 Graph of the outlet temperature of hot water pipe over time

T0= 45 ℃時：

可以看出，此溫度變化的曲線與實際情況吻合很好，0～40 s 為蓄熱期，水管出水溫度始終保持在25 ℃，并且幾乎沒有變化；40～100 s 為溫度拉升期，溫度急劇上升，達到接近穩態溫度的水平；100 s 以后為溫度平穩期，溫度緩慢上升，無限接近穩態溫度。由圖5 還可以看出，提高燃氣熱水器的設定出水溫度，并不能改變蓄熱期的時間，但是能夠顯著改變溫度拉升期的升溫速度，較快達到沐浴所需的最低溫度。

根據式（25）～式（28），時刻t一定時，熱水管道任意x處的溫度（以T0= 48 ℃為例）為：

2 實現熱水零等待的優化設計

由圖5 可以看出，將熱水管里的冷水排凈后，還需等待40 s 水溫才會明顯上升，如果再加上排凈冷水的時間t0，等待時間會更長。

為了縮短等待時間和節約用水，可以在熱水管外壁包裹一層絕熱保溫材料，以及在燃氣熱水器進水口安裝一個熱水循環泵，并增加一個回水管（這兩種方法僅限于新建或者新裝修的住宅）。如圖6 所示，該系統的操作方法及原理如下：用水前，打開熱水循環泵P，熱水循環泵自動檢測進入循環泵的水溫T，若T小于設定的溫度T0，那么，閥門A 關閉，閥門B 打開，熱水管和回水管及燃氣熱水器形成一個閉合的回路（圖中紅色線形成的回路），在水泵P 的作用下按圖示方向循環流動，同時熱水器開啟加熱回路中的水，直到水泵P 檢測到回水管的水溫達到設定的溫度T0，那么閥門B 關閉，閥門A 打開，水路不再循環。之后冷水從閥門A 進入燃氣熱水器，熱水從燃氣熱水器出水口流出，此時打開浴室閥門龍頭即可得到需要的熱水。

圖6 增加熱水循環泵的燃氣熱水器供水系統示意圖Fig.6 Schematic diagram of gas water supply system for adding hot water circulation pump

設浴室出水管在整個熱水管路的最末端（離熱水器最遠），那么增加的回水管也是從熱水管的最末端開始，長度為10 m。由于熱水器出水溫度保持不變，始終為48 ℃，可以看出，在沒有增加熱水管保溫材料情況下，增加了循環泵之后，等待的時間取決于循環泵的抽水速度。如果抽水速度，則等待時間會縮短；如果抽水速度，則等待時間不變，也應該為77 s，但是卻避免了水資源的浪費，在等待77 s 之后，打開水龍頭即可得到熱水。

若在熱水管外壁包裹一層保溫材料（假設保溫材料為膨脹珍珠巖散料，其導熱系數為 0.021W/(m·K)[5]，那么由于保溫材料的導熱系數足夠小，可以視為絕熱[10-12]。對于鋼管而言：

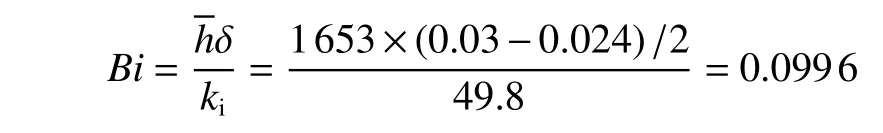
式中：Bi為熱水管傳熱的畢渥數，量綱為一；h為水管水流與管壁間的換熱系數，W/(m2·K)； δ 為水管壁厚度，m。

由于Bi≤0.1 ，因此1.3 節中的非穩態熱傳導推理將不再適用，可采用集中參數法（集總熱容法）對水管傳熱進行分析[7-10]。由于管壁的厚度比其內外徑和長度小得多，因此可合理認為傳熱只發生在徑向上，軸向傳熱可忽略不計。同時，根據集總熱容法的算法要求，x坐標軸徑向上管內壁和外壁之間任一處溫度相同，無溫度梯度。

圖7 所示為增加保溫層的熱水管傳熱分析示意圖。在打開熱水器時，取最先流出的一段微小水柱Δx1進行分析。雖然在從熱水管起始端流到浴室水龍頭末端時， Δx1水柱的管壁外表面空氣溫度始終為25 ℃ ，但是由于不停地和管壁進行換熱而導致溫度不斷降低。設t時刻， Δx1水柱的溫度為Tt1，那么有：

圖7 增加保溫層的熱水管傳熱分析示意圖Fig.7 Schematic diagram of heat transfer analysis of adding insulation layer

式中 ：As為 Δx1水柱與水管內壁接觸的環面積，m2；為水對管壁的換熱系數，W/(m2·K)，根據式（15）的計算結果取 1 653 W/(m2·K) ；U為 Δx1水柱的熱能，J；V為 Δx1水柱的體積，m3。

式（30）進一步細化為：

整理得：

積分得：

式中：tΔ為 Δx1水柱從熱水管起始端流入到末端所需時間，tΔ=t0，由前述t0=L/ω 得t0=36.3 s ；TΔ1為Δx1水柱從熱水管起始端流入到末端時的溫度，K；T0為 Δx1水柱的起始溫度48 ℃。

式（31）進一步簡化為：

代入數據后得到：

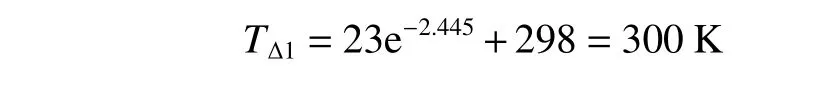
由表達式可以看出，在熱水管外壁包裹一層保溫材料后，打開燃氣熱水器，放掉所有的冷水后（用時36.3 s），理論上出水溫度會立即上升到27 ℃，此后溫度進入拉升區，溫度會迅速上升，而不會像圖5（未加保溫層）那樣有一個蓄熱期，從而大大減少了等待時間和流水浪費。安裝循環泵之后，如果抽水速率和水管中水流速率相同時，只需等待36.3 s 后，即可得到熱水，也不會造成水的浪費。

由以上計算結果可以看出，要縮短熱水等待時間，節約流水，可以從以下幾個方面入手：（1）提高燃氣熱水器出水溫度； （2）縮短燃氣熱水器到浴室龍頭的水管長度；（3）熱水管道加裝保溫材料；（4）加快熱水循環泵的抽水速度；（5）一直開啟循環泵，在不用水的情況下保持燃氣熱水器開啟和熱水管內的水循環。

對于老舊住宅，或者已裝修好的家用燃氣系統，比較好的方法是在浴室安裝一個小型速熱電熱水器（如圖8 所示）。打開燃氣熱水器時，電熱水器首先檢測進入該熱水器的水溫，若水溫低于設定溫度（如42 ℃），則電熱水器開始工作，此時出水即熱，直到電熱水器檢測到燃氣熱水器經熱水管道輸入的熱水溫度達到42 ℃，電熱水器關閉，可實現熱水零等待。

圖8 燃氣熱水器和速熱型電熱水器匹配使用示意圖Fig.8 Schematic diagram of the matching use of gas water heater and fast-heat electric water heater

3 結束語

通過理論模擬計算，得出熱水管安裝絕熱保溫材料和燃氣熱水器安裝循環泵的經濟性和重要性，其亮點在于：

（1）建立了從打開燃氣熱水器開始到穩態傳熱時水管熱傳導的數學模型，以及微元控制體積的微分方程，得到最終出水溫度表達式。

（2）建立了燃氣熱水器的非穩態水管熱傳導數學模型，推導出熱水管出水溫度的微分方程，并用插值擬合法對該非方程進行積分求解，得到出水溫度隨時間變化的函數，模擬結果與實際情況非常吻合。

（3）計算了在包裹絕熱保溫材料時，浴室熱水等待時間，以及經濟性比較。

（4）比較了當同時使用保溫材料和熱水循環泵時，節水情況和熱水等待時間，表明安裝熱水循環泵既能夠增加抽水速度，又能大大減少熱水等待時間。

（5）提出實現熱水零等待的最終解決方案。