基于改進灰狼算法優化BP神經網絡的住宅工程造價預測研究

付家棋，胡國杰

（遼寧工業大學 經濟管理學院，遼寧 錦州 121001）

在建筑工程擬建之前，工程項目的造價預測對可行性分析與項目決策起著重要的作用。在傳統的估算方法中，工程造價的從業人員通過各省頒布的投資估算指標，對工程造價進行預測，由于受到造價人員職業素養和主觀性的影響，工程造價的預測效果并不理想。人工神經網絡具有良好的擬合能力，可以較為準確地預測擬建項目的工程造價，預測的數據可以為工程估算提供有效的參考，郝艷芬等[1]采用BP神經網絡實現了市政工程的造價預測。但是，BP神經網絡存在著搜索能力差、對初始位置較為敏感的缺陷[2]。為加強神經網絡的全局探索能力，潘雨紅等[3]運用遺傳算法優化BP神經網絡，為其賦予最佳的初始迭代位置，加快了收斂速度，準確地預測了公路工程的造價。陳小麗[4]采用粒子群算法優化BP神經網絡，實現了高層住宅工程的造價預測。

2014年Mirjalili等[5]提出了灰狼優化算法（Grey Wolf Optimization Algorithm，GWO）。灰狼算法具有設置參數少和尋優能力強的優點，在預測的準確度和算法時間方面具有良好的表現。但是，灰狼算法存在著種群多樣性單一、全局探索和局部搜索能力不易協調、過早收斂的缺陷。為了改進算法的性能，Nadimi-Shahraki等[6]提出了改進灰狼算法（Improved Grey Wolf Optimizer，I-GWO）。I-GWO采用了一種名為維度學習的搜索策略（Dimension Learningbased Hunting，DHL），增強了灰狼種群的多樣性，平衡了全局探索和局部搜索的能力。

本文將主成分分析降維處理的數據輸入到IGWO-BP模型中進行訓練，通過與其他模型進行對比分析和誤差評價分析，驗證I-GWO-BP模型的有效性。

1 住宅工程造價指標的確定

為展開住宅工程的造價預測，需要輸入一組可以代表工程特征的數據，這些數據不僅能直接反映建筑工程的特點，而且還是影響建筑工程造價的重要因素。按照各分部工程對工程造價的重要性程度，對工程造價指標進行初步選取。通過查閱資料，并對梁喜等[7-16]學者的文獻進行分析，根據造價指標的重要性程度與獲取難易程度進行篩選，最終選取出14項造價指標，同時對定性指標進行量化處理，具體指標見表1。

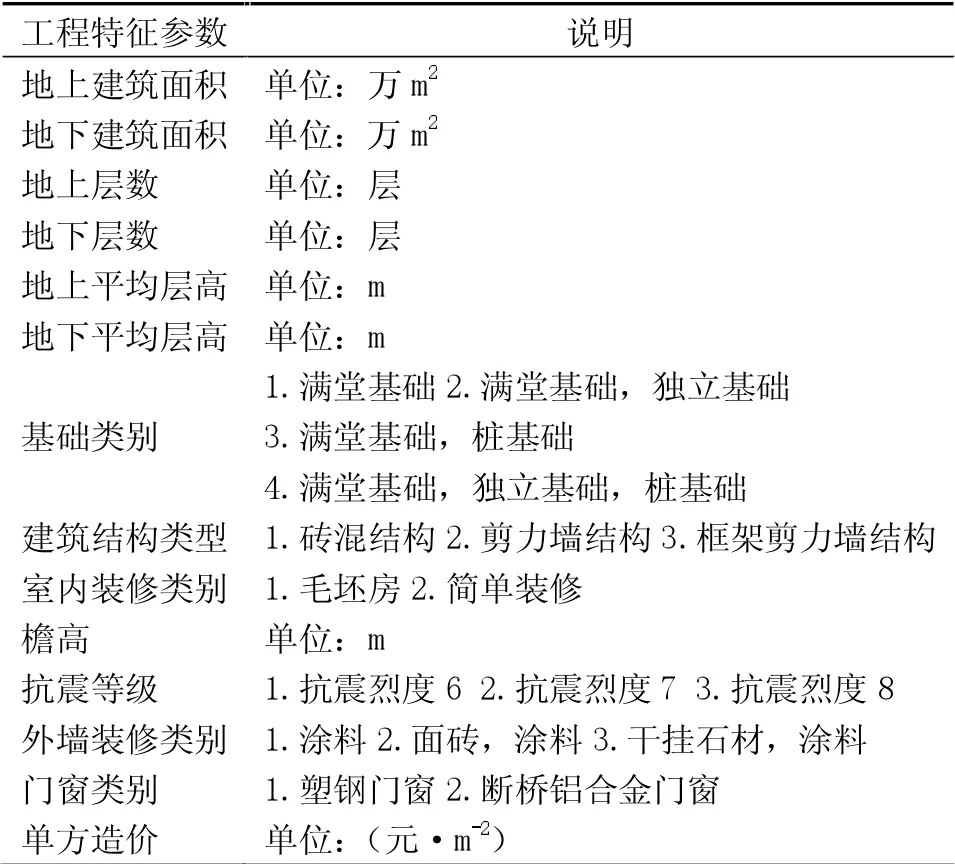
表1 住宅工程造價指標量化表

2 I-GWO-BP預測模型

2.1 灰狼算法

灰狼的種群中存在著特定的等級制度。在算法的搜索過程中，每次迭代時最佳的3只灰狼被定義為α，β和δ，其引導其余的灰狼ω在搜索空間中搜尋獵物。灰狼算法的尋優過程為包圍獵物、狩獵跟蹤、攻擊獵物。

（1）灰狼包圍獵物的模型如下

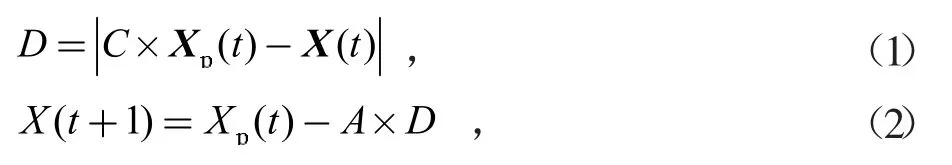
式中：D表示個體與獵物之間的距離；Xp表示獵物的位置向量；X表示灰狼的位置向量；t表示當前的迭代的次數，式（2）表示灰狼位置的更新公式。A和C是系數向量，由式（3）和式（4）計算。

式中：r1和r2是[0，1]之間的隨機值；a為收斂因子。在迭代過程中從2線性減少到0。

（2）灰狼有協作包圍獵物的能力，由適應度最佳的灰狼α，β和δ帶領其余灰狼進行位置更新。灰狼個體的獵物跟蹤模型如下

式中：Dα，Dβ，Dδ分別表示灰狼α，β和δ與其他灰狼ω個體之間的距離；Xα，Xβ，Xδ分別代表灰狼α，β和δ的當前位置；C1，C2，C3的值由式（4）所計算。

式中：X1（t）表示灰狼ω個體朝向灰狼α更新的步長；X2（t）表示灰狼ω個體朝向灰狼β更新的步長；X3（t）表示灰狼ω個體朝向灰狼δ更新的步長。灰狼ω個體最終的更新位置由式（7）所確定。

經過不斷的迭代與更新，獵物最佳的位置將會被確定，即灰狼α所處的位置。

2.2 改進灰狼算法

灰狼算法是在尋優的過程中每只灰狼通過最佳的灰狼引導來進行位置更新的，這就導致了灰狼算法種群多樣性差，易早熟收斂。為了克服灰狼算法的這些缺陷，Nadimi-Shahraki[6]提出了一種選擇和更新相組合的搜索策略。這種搜索策略名為維度學習。DLH的搜索策略提高了全局搜索能力，改善了種群多樣性。改進灰狼算法的搜尋過程為初始化、移動、選擇和更新。

（1）初始化階段：I-GWO進行初始化操作，將N只灰狼隨機分布在搜索空間內，其范圍為[lj，uj]。初始化模型如下

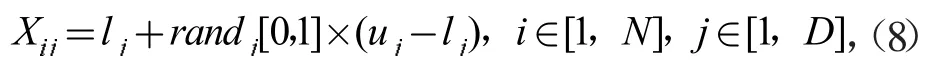
式中：lj和uj分別代表搜索邊界的上下限；randj[0,1]為0到1之間的隨機值。

第i只灰狼在第t次迭代中的位置為實值向量Xi（t）={Xi1，Xi2，…，XiD}，由適應度函數f（Xi（t））計算，其中D為問題的數量。初始化后的狼群被儲存在N行D列的Pop矩陣中。

（2）移動階段：DLH搜索策略與GWO算法搜索策略都會產生一個候選位置來引導灰狼進行位置更新。Xi-GWO（t+1）是GWO算法引導灰狼位置更新的第一個候選位置，由式（7）所計算。首先，在DLH搜索策略中，灰狼個體是向鄰域內不同的灰狼和Pop種群內隨機選擇的灰狼學習的。計算灰狼個體的鄰域半徑，模型如下

式中：鄰域的半徑Ri（t）表示的是當前灰狼位置Xi（t）與候選位置Xi-GWO（t+1）之間的歐氏距離。

然后，在此鄰域內所有的灰狼表示為Ni（t），其中Di為Xi（t）與Xj（t）之間的歐氏距離。

最后，DLH搜索策略為灰狼Xi（t）提供另一個更新的候選位置，表示為Xi-DLH（t+1），模型如下

式中：Xi-DLH，d（t+1）的第d維是由Ni（t）中隨機選擇的灰狼XN，d（t）的第d維與Pop種群中隨機選擇的灰狼Xr，d（t）的第d維進行計算的。對灰狼的第d維執行此操作后，迭代計數器加1，直到達到最大的迭代次數D完成候選位置的更新操作，其中D為問題的維數。

（3）選擇和更新階段：通過比較Xi-GWO（t+1）與Xi-DLH，d（t+1）的適應度值來選出最佳的候選位置。如果最佳候選位置Xi（t+1）的適應度值優于灰狼個體Xi（t），則進行位置更新，否則，灰狼Xi（t）的位置保持不變。

所有灰狼個體完成位置更新后，迭代計數器加1，直到達到預先設定的迭代次數。

2.3 基于I-GWO優化BP神經網絡

若誤差函數存在多個峰值，BP神經網絡沿著負梯度方向尋找最優解的過程中易陷入局部極小點，預測結果產生的偏差較大。然而，I-GWO算法的全局搜索能力較強，可以為神經網絡尋找出全局最優解。使用BP神經網絡的誤差函數作為I-GWO算法的適應度函數，通過BP神經網絡連接權值和閾值的數量來決定I-GWO算法中灰狼的維數，那么I-GWO算法尋優的過程就是權值和閾值更新的過程。因此，I-GWO算法尋優的過程替代了BP神經網絡梯度下降的過程[17]。經過不斷更新和迭代，最終確定出全局最優值，即灰狼α所處的位置。最后將灰狼α的位置映射為BP神經網絡的權值和閾值，并結合BP神經網絡公式對樣本數據進行擬合和預測。改進灰狼算法優化BP神經網絡的算法過程如下。

步驟1：確定神經網絡的節點數量和激活函數，適應度函數選用均方誤差（Mean Square Error，MSE）。

步驟2：確定初始化參數。包括灰狼的維數、參數的上下界、灰狼的種群數量及最大的迭代次數。

步驟3：初始化灰狼位置。將N只灰狼隨機的分布到搜索空間，并計算每只灰狼的適應度。

步驟4：選取出適應度最佳的3只灰狼α，β和δ。根據式（7）計算出第一個候選位置Xi-GWO（t+1），并更新參數A，C和a。

步驟5：根據式（9）計算出鄰域的半徑Ri（t），并構建Ni（t）的鄰域矩陣。

步驟6：根據式（11）計算另一個候選更新位置Xi-DLH，d（t+1），并判斷每一維度是否存在越界行為。

步驟7：比較Xi-GWO（t+1）與Xi-DLH，d（t+1）的適應度值，選出最優的候選位置。如果所選擇的最佳候選位置劣于Xi（t），則Xi（t）作為最佳候選位置。

步驟8：判斷是否達到最大迭代次數，若是算法結束，否則執行步驟4到步驟7。

步驟9：將最優解的位置映射為神經網絡的權值和閾值，并輸入到神經網絡的公式中進行擬合與預測。

3 實例分析

3.1 數據選取

樣本數據源于“廣聯達造價指標網”和“鄭州市建設信息網”，共收集了31組2013—2019年之間河南地區住宅工程造價數據。由于各地區經濟發展水平的不同和編制時間的差異，以河南省鄭州市2019年第一季度造價指標作為基準，對31組單方造價指標進行比例換算。河南省住宅工程造價部分數據見表2。

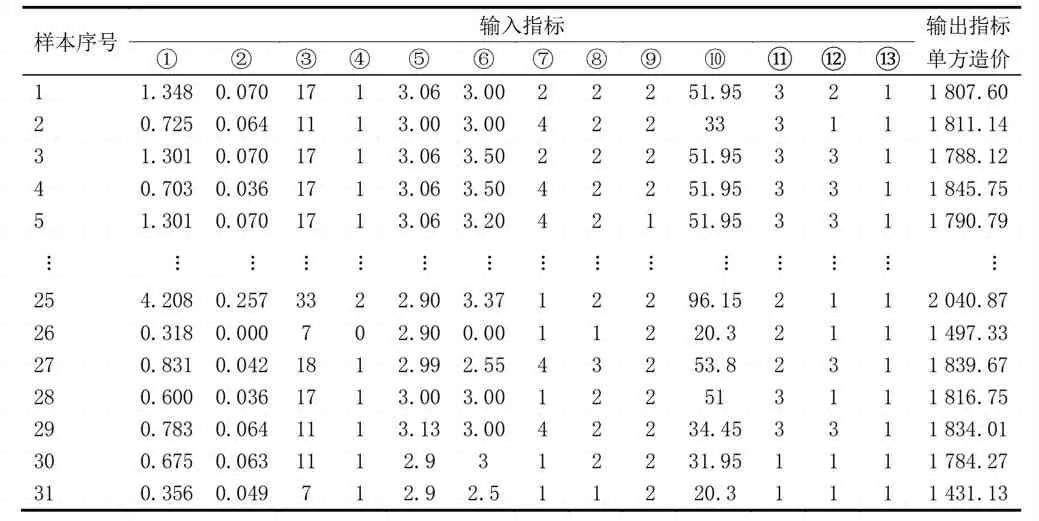
表2 河南省住宅工程造價數據（部分）

3.2 主成分分析

由于各工程造價指標的量綱不同，并且數量級差距過大。在主成分分析之前，需要對31組造價數據進行標準化處理。本文采用標準分數法（Z-SCORE）對原始數據進行標準化操作，并將處理好的數據導入SPSS中進行主成分分析。各主成分的方差百分比與累計貢獻率見表3。

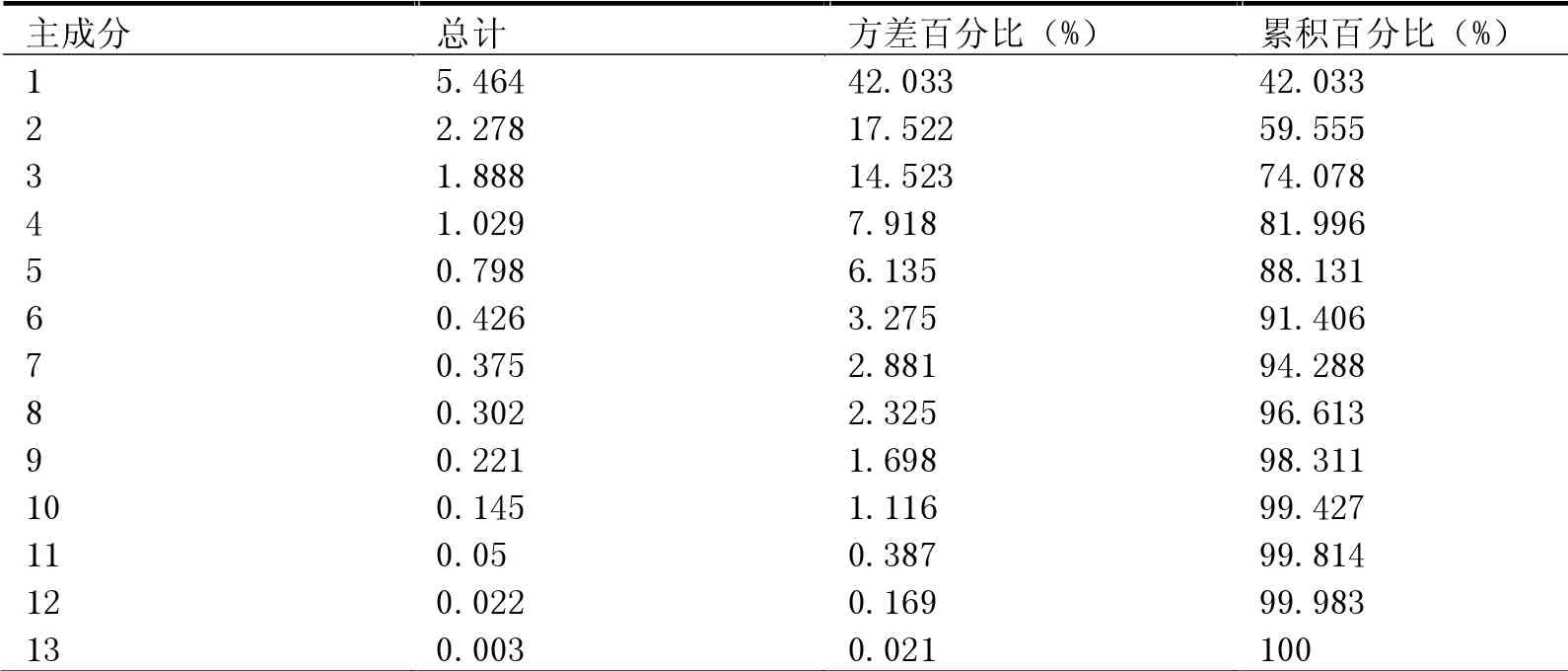
表3 方差百分比與累計貢獻率

樣本數據KMO為0.65大于要求的0.5，并且巴特利特顯著性為0，證明該組數據適合進行主成分分析。本文選取前7個累積貢獻率達94.29%的主成分作為預測模型的輸入集，并進行訓練與仿真。

3.3 模型的訓練與仿真

選擇河南省造價數據集前24組作為訓練樣本，剩余7組作為檢驗樣本。I-GWO算法的參數設置如下：算法初始化邊界范圍為[-3，3]，灰狼個數N=150，最大的迭代次數為1 000次。BP神經網絡采用7-7-1的拓撲結構，使用sigmoid作為激活函數。同時，通過多模型對比分析，驗證I-GWO-BP模型的有效性。其中GWO算法的參數設置與I-GWO算法保持相同，PSO算法的參數設置如下：慣性權重w采用線性遞減的策略wmax=0.9，wmin=0.5,學習因子c1=c2=2，粒子個數N=100，最大訓練次數為1 000次。傳統BP神經網絡、粒子群算法、傳統灰狼算法與改進灰狼算法的預測結果對比如圖1所示。算法的誤差曲線如圖2所示。

由圖1可知，BP神經網絡的預測誤差最大，貼合度最差。同時在算法執行的過程中發現神經網絡具有較強的隨機性，需要多次訓練才能達成滿意的結果，預測穩定性最差。隨著優化算法的加入，預測結果準確度和穩定性有了很大的改善。其中I-GWO算法的預測結果與真實結果最為貼近，在貼合度和預測準確性上要優于其他算法。

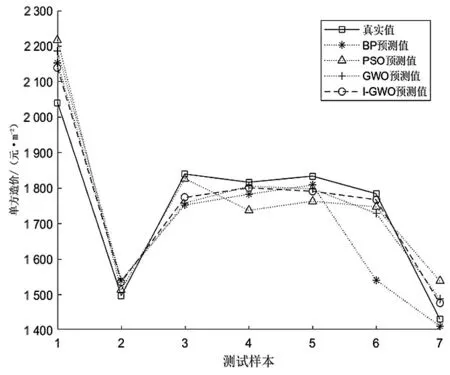
圖1 不同算法預測結果對比

從圖2可知，PSO算法誤差曲線下降緩慢，并經過一段時間的迭代后誤差停止減少，訓練誤差最大。其原因是在PSO算法尋優的過程中陷入了局部極小點，同時PSO算法也無法從中脫困，導致了預測的準確度較差。GWO算法前期收斂速度較慢，隨著迭代次數的增加誤差仍然可以繼續降低，最后也可以達到理想的誤差精度。I-GWO算法誤差曲線下降速度最快，誤差的精度較高，說明該算法的全局尋優能力較強。

圖2 不同算法誤差曲線對比

3.4 預測結果分析

本文使用平均誤差Mean、均方根誤差RMSE、擬合優度對各預測模型進行評價。各算法運行20次，并選取各評價結果的均值進行對比，結果見表4。

由表4可以看出I-GWO算法的預測模型要明顯優于其他算法，I-GWO算法的均方根誤差最小，平均誤差最小，擬合優度最大，說明該模型預測的準確度較高。I-GWO-BP模型的最大均方根誤差為67.89元/m2，最小均方根誤差為53.17元/m2。同時I-GWO-BP模型最大相對誤差為3.48%，最小相對誤差為2.63%，其預測誤差滿足可行性研究階段10%的誤差要求。IGWO-BP預測模型在住宅工程的造價預測中具有實際的現實意義。

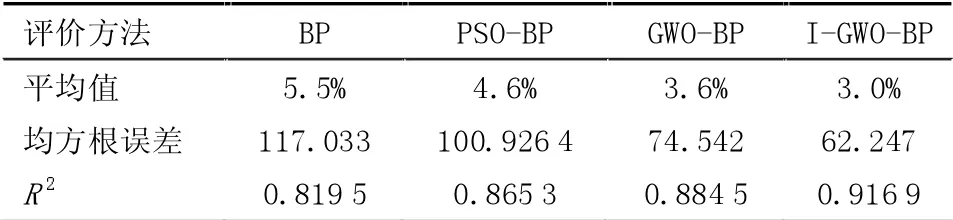
表4 不同模型預測結果對比

4 結束語

本文采用I-GWO-BP模型對住宅工程造價進行預測，有以下結論：

（1）I-GWO-BP模型可以對中高層、高層和超高層住宅的工程造價做出很好的區分，并根據建筑的特點和往年的造價數據實現了住宅工程的造價預測。

（2）采用主成分分析法篩選工程造價指標，選取出7個累計貢獻率為94.29%的造價指標，簡化了輸入數據，提高預測準確度。

（3）使用I-GWO算法代替BP神經網絡梯度下降的過程，增強了神經網絡的全局搜索能力，預測結果更加準確。I-GWO-BP模型預測結果滿足可行性研究階段的誤差要求，可以作為房地產估價師的輔助工具。