Ti2AlNb 合金的嵌入原子勢*

劉杰 劉艷俠

(遼寧大學物理學院,沈陽 110036)

分子動力學模擬是一種行之有效的計算機模擬方法;然而,由于缺少合適的多元合金原子間勢,因而限制了分子動力學模擬的應用.多元合金原子間勢的開發一直具有挑戰性.本文在嵌入原子勢模型的框架下,提出一種適用于三元有序合金的原子間勢構建方法,并開發了適用于原子尺度力學行為模擬的Ti2AlNb 合金新型原子間勢.該勢能夠很好地再現B2-Ti2AlNb 的彈性常數、未弛豫的空位形成能、置換原子形成能、換位原子形成能、表面能和三種有序構型(B2 相、D019 相、O 相)在不同體積下的內聚能.為了進一步檢驗勢函數,計算了B2 相的E-V 曲線,結果與Rose 曲線符合得很好;利用分子動力學模擬研究了B2 相的熔化轉變過程,結果大致反映了實驗情況.本文的工作一方面為開發多元合金原子間勢提供一種途徑,另一方面為模擬計算Ti2AlNb 合金的工作者提供一種選擇.

1 引言

目前開發原子間勢主要有兩類方法: 一類是近幾年發展起來的機器學習法[1];另一類是傳統的擬合原子間勢參數的方法.

隨著人工智能的快速發展,機器學習法開發原子間勢應用而生,已經有許多成功應用的案例[2,3],Smith等[4]在2020 年用機器學習的方法構建了鋁元素的原子間勢,他們應用了多種神經網絡來訓練大量數據,比如由金屬的不同結構的多種性質,最后得到了計算精度非常高的原子間勢.機器學習法構建原子間勢的優勢在于減少了人為干預的成分,規避了傳統方法建勢的參數化問題,且可以達到與第一原理方法相媲美的精度[5].但是機器學習勢的非物理形式阻礙了對模型參數的直接解釋,并阻止了對參考數據集沒有很好描述的構型空間區域的外推,同時機器學習勢需要準備大量準確的訓練數據集.

傳統方法構建原子間勢也同樣具有一定的優勢,首先構建的勢函數形式簡單,與分子動力學接口友好,需要準備的擬合數據數量遠少于機器學習勢,加之人工特有的跨學科優勢,擬合過程中可根據物理理論進行人為干預,可以更加靈活地調整參數,且擬合過程中的每一步都具有清晰的物理意義.

Ti2AlNb 合金具有很多優異性能,如高強度、高比模量以及較高的抗氧化性等[6-9],使其成為航空航天發動機的首選材料之一.關于Ti2AlNb 合金的實驗研究,可采用摻雜、多種強化機制及熱處理等工藝來改善合金的使用性能[10].理論研究主要采用第一原理計算的方法.如Pathak 和Singh[11]用第一原理方法計算了三種有序構型(B2 相、D019相、O 相)結構的穩定性,并給出了各自的晶體結構、空間群、原子坐標等信息.

由于缺少合適的Ti2AlNb 合金原子間勢,因而限制了使用分子動力學模擬的方法研究Ti2AlNb合金的性能.Ti2AlNb 基合金一般由α2,O,B2 中的兩相或三相構成.β/B2 都是bcc 結構,β是無序相,B2 是有序相.Nb是β相的穩定元素,由于Ti2AlNb 基合金中Nb 含量比較高,所以β相穩定元素一直存在,且B2 相滑移系較多,是塑性相,因此,本文采用傳統方法主要針對B2 相開發Ti2AlNb合金原子間勢,期望能為分子動力學模擬工作者提供一種選擇.

2 原子間勢的構建

2.1 模型

本文選用嵌入原子 (embedded-atom method,EAM)勢模型[12],在該模型下體系的總能為

其中α,β,γ,?,σ,μ為擬合參數;rc為截斷距離;h為截斷函數形狀的調整參數,截斷函數形式為

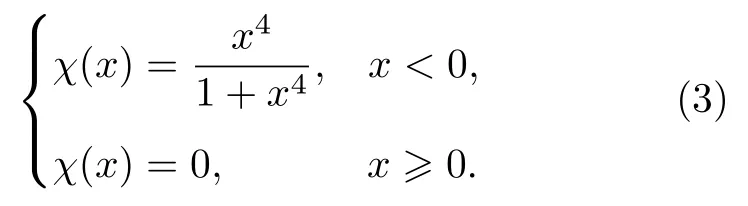
對于本文的三元合金原子間勢的構建,需要擬合三種交叉對勢,分別為?(rTiAl),?(rTiNb)和?(rNbAl),包含18 個擬合參數,再加上sx和gx(下標x表示Ti,Al,Nb 的任意一種元素),共24 個擬合參數,截斷距離選用相同的值為rc.

在擬合合金的原子間勢時,應用了關于以下規范變換的不變性[14,15]:

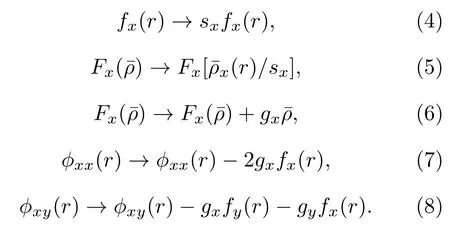
x和y代表Ti,Al,Nb 三種元素中的任意一種,上述變換中sx和gx是任意常數,對于三元有序構型比如B2-Ti2AlNb 合金,不是嚴格意義滿足能量對其公式變換的不變性(本質上這種變換關系對于合金需要滿足高度有序的對稱性,規范變換會改變勢函數的形狀).對于A-B-C 體系,可以使變換后的多體勢滿足[14],這樣多體勢函數就可以在平衡狀態下對應原子的電子密度處取得極值(通常情況下為極小值)[16],本文在B2 相的環境中使其滿足的值由歸一化條件確定,此外本文盡量使和的值接近1.

2.2 擬合數據庫

關于Ti2AlNb 合金性能的實驗值非常有限,因此本文主要使用第一原理計算的數據來參數化原子間勢.使用基于密度泛函理論的VASP 軟件(Viennaab-initiosimulation package),交換關聯泛函選擇Perdew-Wang 91 形式,平面波截斷能為500 eV,總能收斂標準為10—5,原子弛豫最大步數為100,采用共軛梯度算法(CG 算法)優化原子的位置,k點選取因晶體結構的差異和計算物理量的不同而略有不同.本文用于擬合的數據庫包括:B2 相的晶格常數如表1 所列;三種純金屬Ti,Al,Nb 的內聚能,如表2 所列;B2 相的彈性常數如表4 所列;B2 相的未弛豫的單空位形成能和雙空位形成能如表5 所列;B2 相的置換原子形成能和換位原子形成能如表6 所列;B2 相的內聚能如表8 所列.

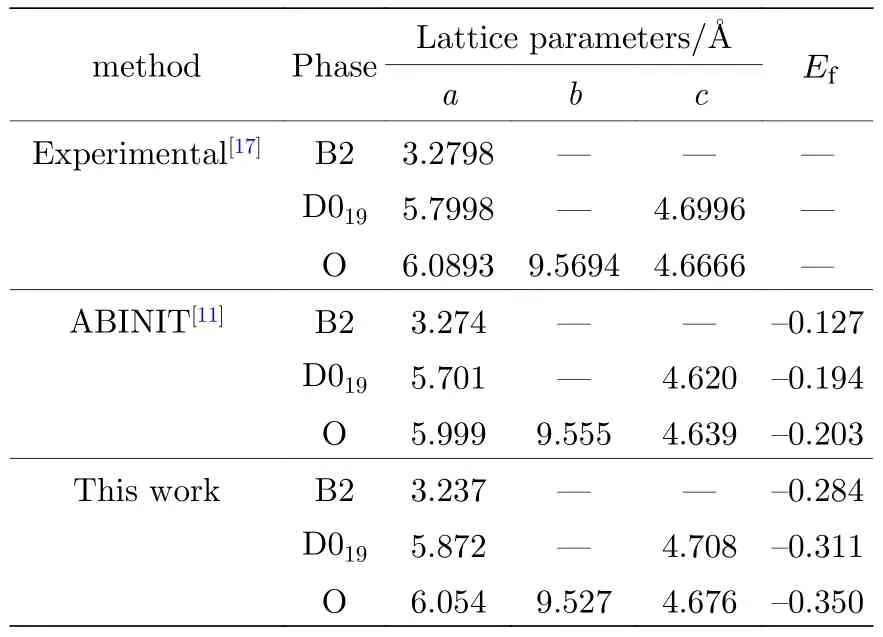
表1 B2-Ti2AlNb 的晶格常數和生成焓(單位: eV)Table 1.Lattice constants and formation enthalpy for B2-Ti2AlNb (in eV).

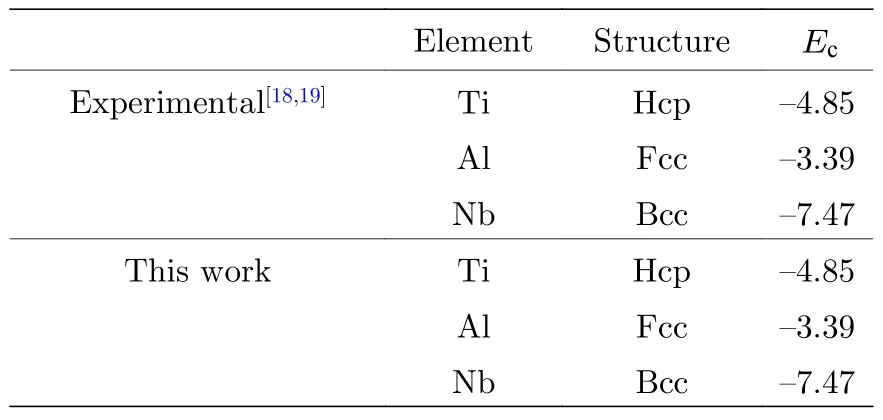
表2 單質Ti,Al,Nb 的內聚能(單位: eV)Table 2.Cohesive energies for Ti,Al and Nb (in eV).

表1 中同時列出了實驗值和文獻[11]的計算結果,可以看出,本文的計算結果與實驗值和文獻[11]的結果都非常接近.

2.3 原子間勢函數參數化

為了對原子間勢函數進行參數化,以及檢驗原子間勢的質量,需要使用原子間勢表示各個物理量.本文考慮了長程相互作用,原子間勢的截斷距離設置在第六和第七近鄰之間,且需要給出Ti,Al,Nb 三種元素之間的對勢及電子云之間的相互作用,因此解析表達式比較復雜.為此本文主要通過程序設計來建立物理量與原子間勢的關系.設計思想是,先建立原子構型模塊,包含原子空間坐標、原子類型和原子編號等信息,然后在此基礎上,根據相應的理論進行各種物理量的計算.這里只介紹本文使用的彈性常數和空位形成能的計算公式.

根據彈性理論,可以得到平衡狀態下彈性常數與原子間勢之間的關系為[20]

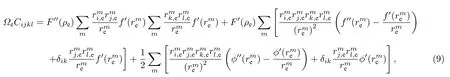
根據(1)式,可以得到平衡狀態下空位形成能與原子間勢的關系式為[21]

在確立了物理量與原子間勢的關系和擬合數據庫之后,利用能量最小化的方法,同時考慮了物理量的權重,擬合了原子間勢函數的參數,如表3 所列.

表3 Ti2AlNb 合金EAM 勢的擬合參數Table 3.Fitting parameters of EAM potential for Ti2AlNb alloys.

在擬合之前,已將B2 相構型中的Ti 原子的背景電子密度歸一化,由此將限制sTi,sAl,sNb三者之間的關系,為了確保電子密度函數曲線在x軸上方,在擬合過程中已限制三者的符號均為正.對于Ti 原子,在電子密度歸一點處嵌入能函數達到最低點,而對于Al 和Nb 原子而言,在擬合過程中盡力使其接近1.其中參數sTi,sAl,sNb的值分別為0.3333,0.4646,4.1557,參 數gTi,gAl,gNb的值分別為—7.3047×10—7,—0.0640,—0.6733,由此可以得到EAM 型原子間勢的各函數如圖1 所示.

3 結果與討論

作為對原子間勢的測試及應用,利用開發的Ti2AlNb 合金的EAM 勢研究了B2-Ti2AlNb 的彈性常數、點缺陷、表面能、熔點性能,以及Ti2AlNb合金三種有序相的E-V關系.

3.1 彈性常數

B2-Ti2AlNb 晶胞的空間點陣屬于正方晶系,其晶格常數滿足a=b≠c,α=β=γ=90°,彈性常數[22]滿足C11=C22,C55=C66,C13=C23,計算比較了B2 相的6 個彈性常數(C11,C33,C44,C55,C12,C13),利用本文開發的EAM 勢和第一原理的計算結果如表4 所列.

由表4 可以看出,本文開發的EAM 勢的計算結果與第一原理(DFT)計算結果基本一致.

表4 B2-Ti2AlNb 的彈性常數(單位: GPa)Table 4.Elastic constants for B2-Ti2AlNb (in GPa).

3.2 空位形成能

單空位及雙空位形成能[23]的計算方法分別為:

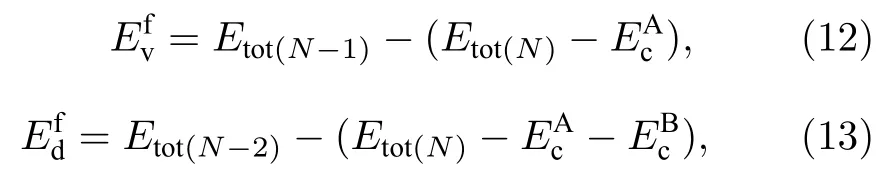
其中,Etot(N)表示理想超胞總能,Etot(N-1)表示去掉一個原子的超胞總能,Etot(N-2)表示去掉兩個原子的超胞總能,和分別表示去掉的單質原子A 和原子B 的內聚能.本文所有關于空位形成能的計算結果均列于表5 中,表5 中第二列表示去掉的原子類型,后面的數字表示第幾近鄰,例如AlNb-1 表示去掉超胞中最近鄰的Al 和Nb 兩個原子.

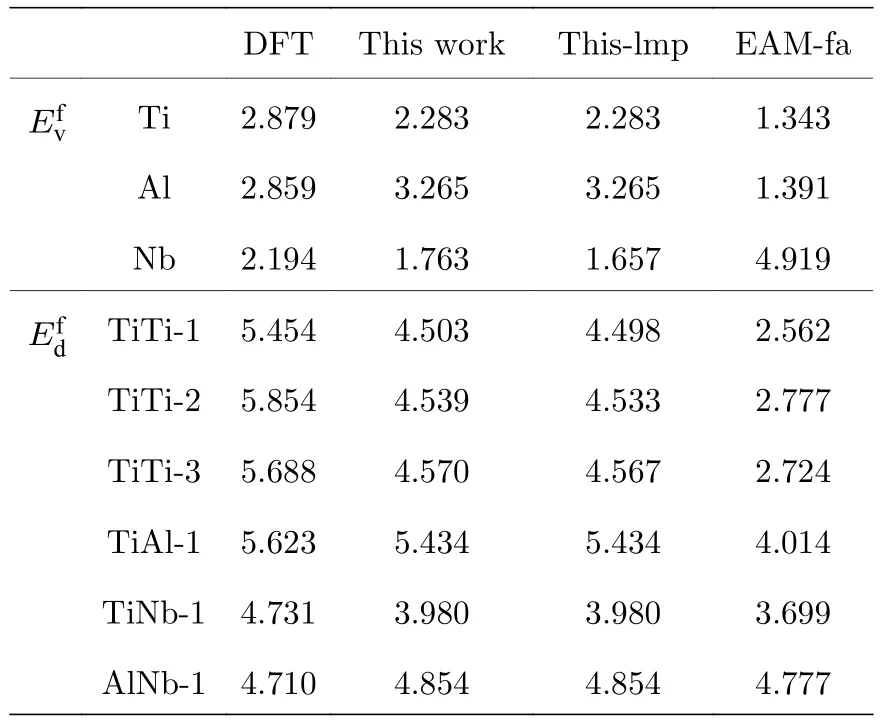
表5 B2-Ti2AlNb 單空位形成能和雙空位形成能(單位: eV)Table 5.Mono-vacancy formation energies and divacancy formation energies for B2-Ti2AlNb (in eV).

表5 中標注“This work”這一列的值是利用本文開發的EAM 勢編程計算得到的,標注“Thislmp”的這一列表示利用本文開發的EAM 勢,使用Lammps 軟件進行模擬計算的結果.標注“EAM-fa”這一列表示本文利用Farkas[24]開發的EAM 勢的計算結果,計算工具使用的依然是Lammps 軟件.由圖2 所示的空位形成能的對比圖可以看出,本文開發的EAM 勢,用兩種方法的計算結果幾乎完全一致,相比于用Farkas[24]的勢整體上更接近第一原理計算結果.

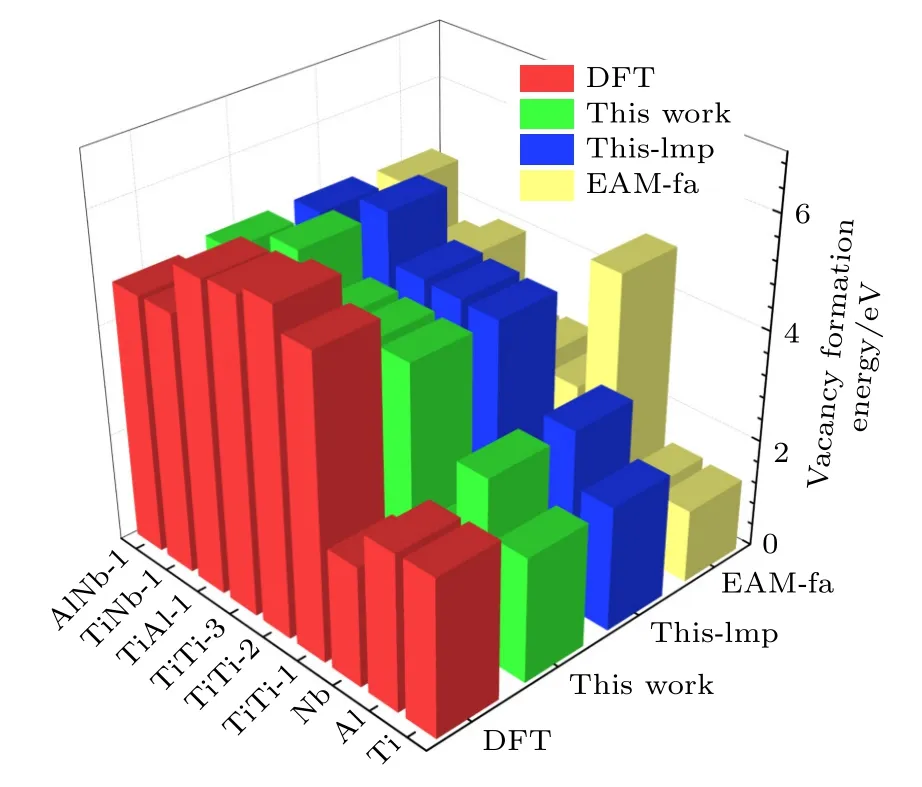
圖2 B2-Ti2AlNb 單空位形成能與雙空位形成能Fig.2.Mono-vacancy formation energies and di-vacancy formation energies for B2-Ti2AlNb.

3.3 置換和換位原子形成能

利用本文開發的EAM 勢計算了B2 相的置換原子形成能,同時計算了截斷距離范圍內交換原子位置的形成能,即換位原子形成能.在圖3 中已經清晰地表示出原子換位及其表征情況,其中紅色、綠色、藍色的原子分別表示Ti,Al,Nb.置換原子形成能為

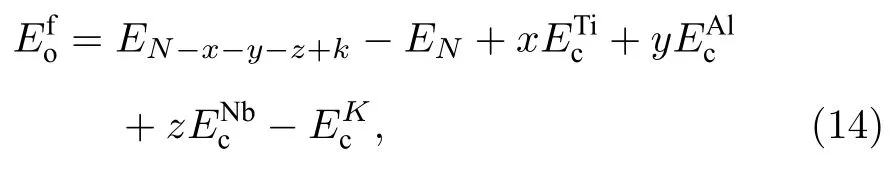
圖3 B2-Ti2AlNb 原子位置換位示意圖Fig.3.Atom position transposition diagram for B2-Ti2AlNb.

EN-x-y-z+k表示有缺陷的超胞總能,EN表示理想超胞的總能,表示單質Ti,Al,Nb,K原子的內聚能,K表示用于置換的原子的類型.x,y,z的值可以是0 或±1,分別表示被置換原子Ti,Al,Nb 的數目,k表示用于置換的原子的數目.例如滿足x=z=0,y=1,K=Ti 的組合表示在Al 原子的點陣上置換一個Ti 原子,用(T iAl)表征,其他置換原子的形成能也采用這種表征方式.對于換位原子的形成能可表示為

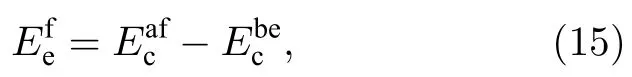
式中表示換位后超胞的總能,表示理想超胞的總能.

從表6 可以看出,本文開發的EAM 勢計算的多種置換原子和換位原子的形成能更接近第一原理計算結果,從圖4 和圖5 可以更清晰地看到這一結果,與第一原理相比,各種形成能的誤差最大也沒有超過0.233 eV,表明該EAM 勢能很好地描述Ti2AlNb 合金的點缺陷性質.

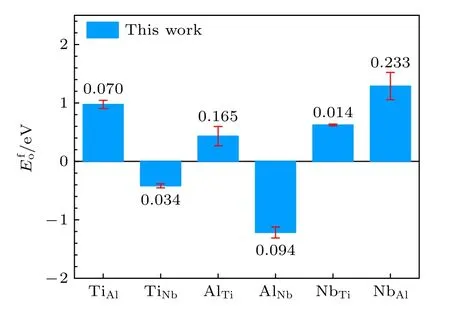
圖4 B2-Ti2AlNb 置換原子形成能的誤差Fig.4.Deviations of substitutional atom formation energies for B2-Ti2AlNb.

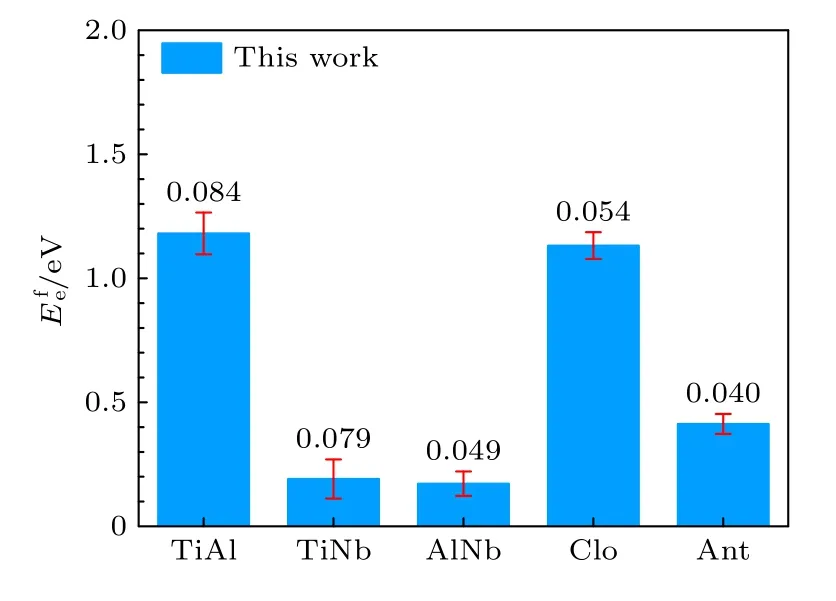
圖5 B2-Ti2AlNb 換位原子形成能的誤差Fig.5.Deviations of transposition atom formation energies for B2-Ti2AlNb.

表6 B2-Ti2AlNb 置換原子和換位原子形成能(單位: eV)Table 6.Substitutional atom and transposition atom formation energies for B2-Ti2AlNb (in eV).

3.4 表面能

平衡態下,理想晶胞中的原子受周圍原子作用的合力為零,處于能量最低的狀態,但位于表面上的原子所受的周圍原子的合力不為零,因而能量較高,減去沒有表面時體系的能量再除以該表面的面積,即為該表面的表面能,表面能的計算公式為

式中為表面能;ES表示具有表面時體系的總能;Et表示沒有表面時體系的總能;Ssur為體系中形成表面的面積.本文計算了B2 相中(100)面和(110)面的表面能,形成表面的體系在平行于表面的方向上利用了周期性邊界條件,在垂直于表面的方向上設置了擴胞和真空層,具體的計算結果如表7 所示,表7 中標記一撇“'”的表面表示對該表面進行了能量最小化.從表7 中可以發現本文開發的EAM 勢關于(100)和(110)兩表面能的計算結果與第一原理計算結果趨勢一致,都表明(110)面的表面能更小.

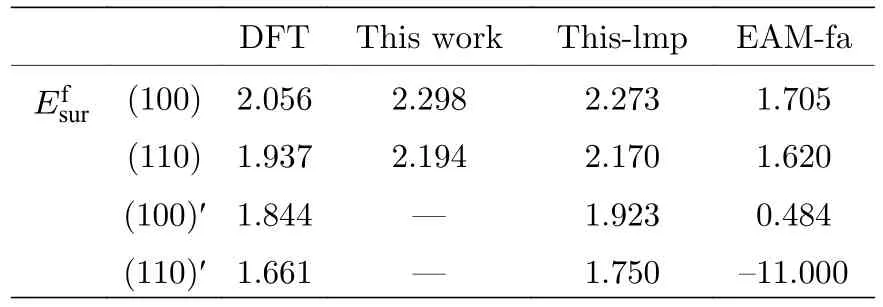
表7 B2-Ti2AlNb 的表面能(單位: eV)Table 7.Surface energies for B2-Ti2AlNb (in eV).

3.5 E-V 曲線

為了檢驗原子間勢偏離平衡態時的表現,利用本文開發的EAM 勢推導了Ti2AlNb 合金三種有序相的E-V關系.考慮到合金中Ti,Al,Nb 三種原子的周圍環境不同,因此計算了分別以Ti,Al,Nb 三種原子為參考原子的E-V關系,合金中以Ti 原子為參考原子的E-V關系為

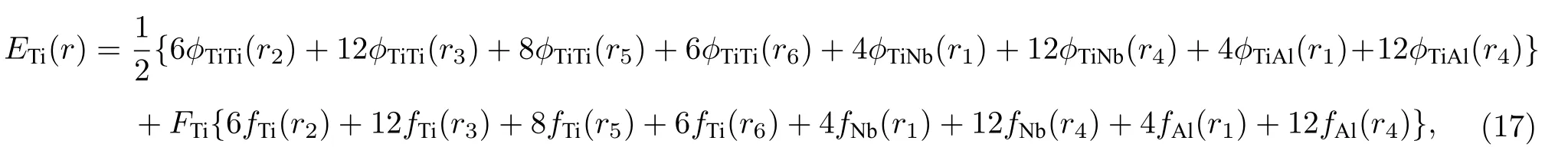
式中,r1表示B2 相合金中最近鄰距離,r2表示次近鄰距離,以此類推,rn表示第n近鄰距離.電子密度函數fTi(rn) 表示為第n近鄰的Ti 原子貢獻的電子密度,前面的數字表示該原子的數目.

同理,可以得到分別以合金中Al 原子和Nb 原子為參考原子的E-V關系為

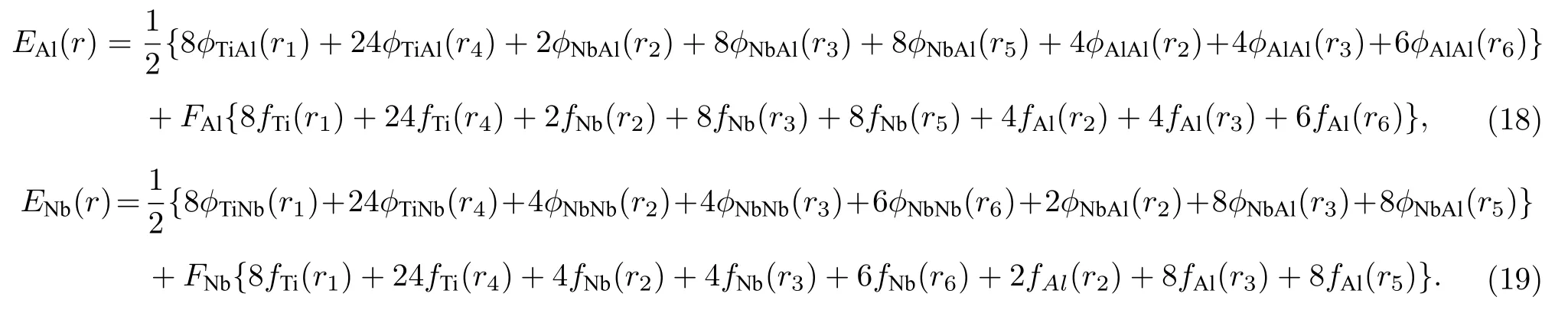
對上述三種E-V關系進行加權平均,便可得到Ti2AlNb 合金中平均每個原子的E-V關系,如(20)式所示:

本文計算的B2相E-V關系曲線如圖6 所示,同時為了比較,根據Rose 的經驗公式[25]計算了E-V關系,同時畫在圖6 中.

由圖6 可以看出,在距離小于約3.3 ?的范圍內擬合曲線與Rose 曲線吻合非常好,同時表明曲線在體系處于平衡狀態時的曲率相近,彈性模量一致.超過這個范圍兩曲線雖然略有差距,但整體變化平穩,沒有出現過多的振蕩.

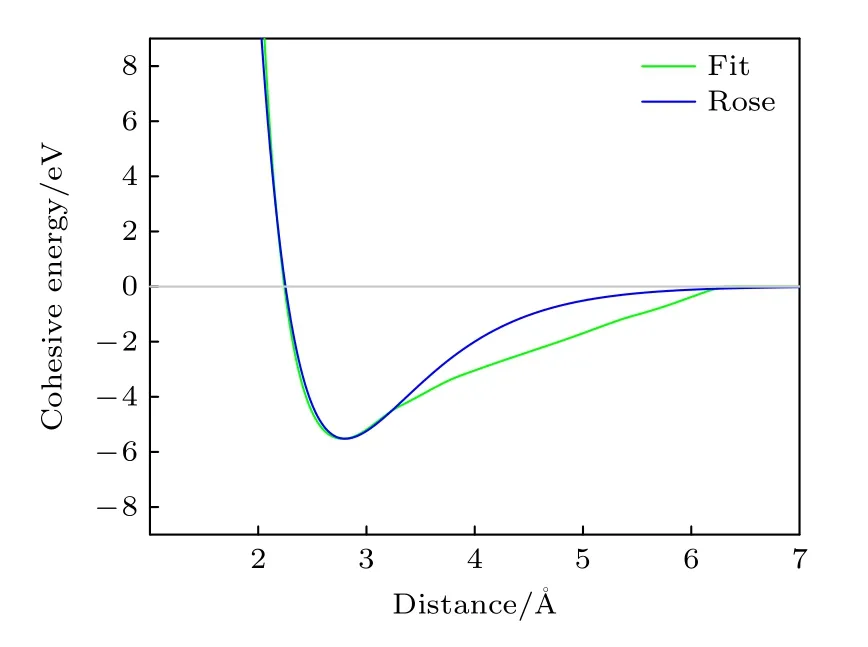
圖6 B2-Ti2AlNb的E-V 曲線與Rose 曲線Fig.6.E-V curve and Rose curve for B2-Ti2AlNb.

為了驗證本文開發的EAM 勢對于Ti2AlNb合金不同相的描述能力,使用第一原理方法計算了平衡狀態下B2 相、D019相、O 相在不同體積下的內聚能,計算結果見表8,三種有序相的E-V曲線如圖7 所示.從圖7 可以發現: 對于B2 相,該EAM 勢的計算結果非常接近第一原理的計算結果,Farkas[24]的結果在體積膨脹超過20% 時變化非常緩慢,不太適合這個范圍;對于D019相,本文的EAM 勢的計算結果相比Farkas[24]的計算結果更接近第一原理計算結果;對于O 相,本文的結果不僅與第一原理的結果的趨勢完全一致,偏差也非常小,Farkas[24]的結果與第一原理的計算偏差也不大,而且曲線的左側,即當晶體被壓縮時,Farkas的結果與第一原理的結果趨勢也完全一致,但是曲線右側的變化趨勢與第一原理計算結果不太一致,也就是當晶體膨脹時,Farkas 的結果比第一原理的結果變化緩慢.

圖7 Ti2AlNb 合金的E-V曲線 (a) B2 相;(b) D019 相;(c) O相Fig.7.E-V curve of Ti2AlNb alloys: (a) B2 phase;(b) D019 phase;(c) O phase.

3.6 熔點

利用本文開發的EAM 勢通過分子動力學模擬研究了B2 相的熔化轉變過程,模擬盒子的大小為3456 個原子的超胞,在初始B2 相構型下保持初始溫度,并在NVT 系綜下進行弛豫,升溫的過程在NPT 系綜下進行,期間原子體積在0 至1400 K 附近的溫度范圍內呈線性增加,如圖8 所示.圖8中可以看出B2-Ti2AlNb 合金在1400 K附近發生一級相變,單位體積發生突變,正如圖9 所示,體系在此溫度附近前后從有序構型轉變為無序狀態.圖9 中紅色、綠色、藍色的原子分別表示Ti,Al,Nb.

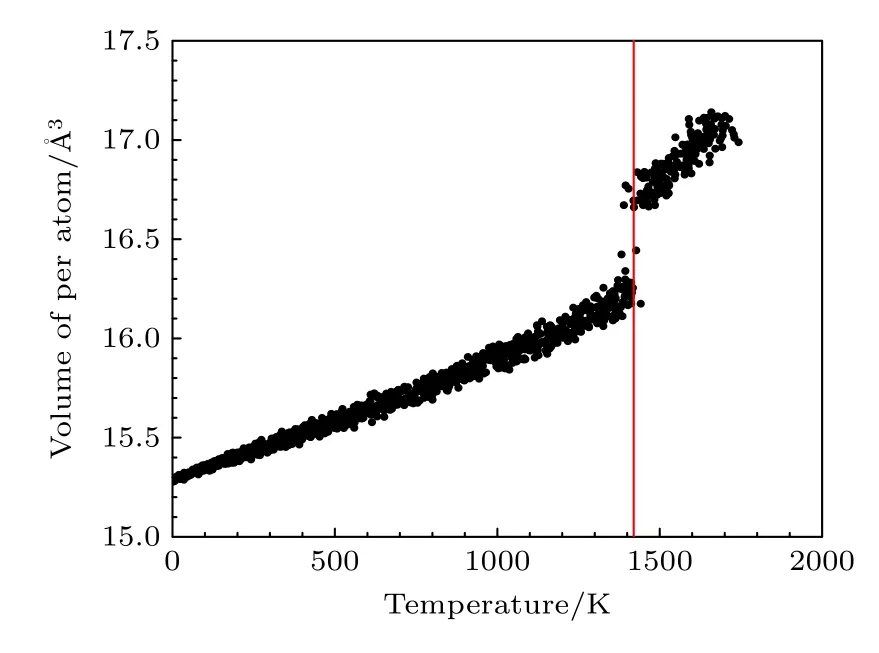
圖8 B2 相的每個原子的體積隨溫度的變化Fig.8.Volume variation of each atom for B2 phase as functions of temperature.

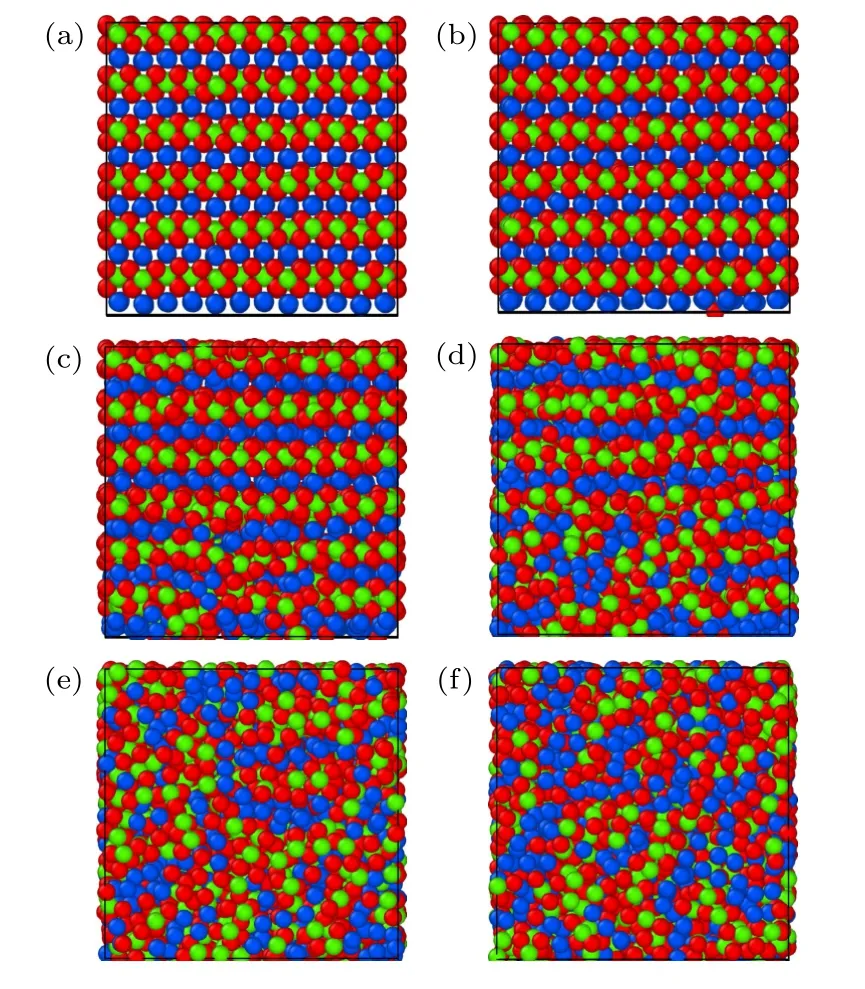
圖9 B2 相隨溫度變化的截面快照 (a) 296 K;(b) 754 K;(c) 1428 K;(d) 1390 K;(e) 1449 K;(f) 1728 KFig.9.Cross-section snapshots for B2 phase as functions of temperature: (a) 296 K;(b) 754 K;(c) 1428 K;(d) 1390 K;(e) 1449 K;(f) 1728 K.

從Ti-Al 平衡相圖[26]中看出,Ti3Al 合金的熔點大于1900 K,向Ti3Al 基合金中摻雜Nb 可以提升合金的綜合性能,而Ti-22 Al-26 Nb 合金B2 相的熔點大約為1873 K[27],以此為參考,利用本文開發的EAM 勢計算的Ti2AlNb 合金的熔點比此溫度低了約25%.由于本文主要針對Ti2AlNb 合金的力學性能開發EAM 勢,擬合數據庫中未包含與溫度相關的數據.一般來說,同一種勢函數形式很難同時描述低溫和高溫的性能,考慮有兩種改進方案,一是在擬合數據庫中加入相變等與溫度相關的數據,在保證不影響對力學性能描述的基礎上,改善勢函數描述高溫性能的能力;另一種是針對高溫性能開發新的原子間勢,只用于預測高溫性能.

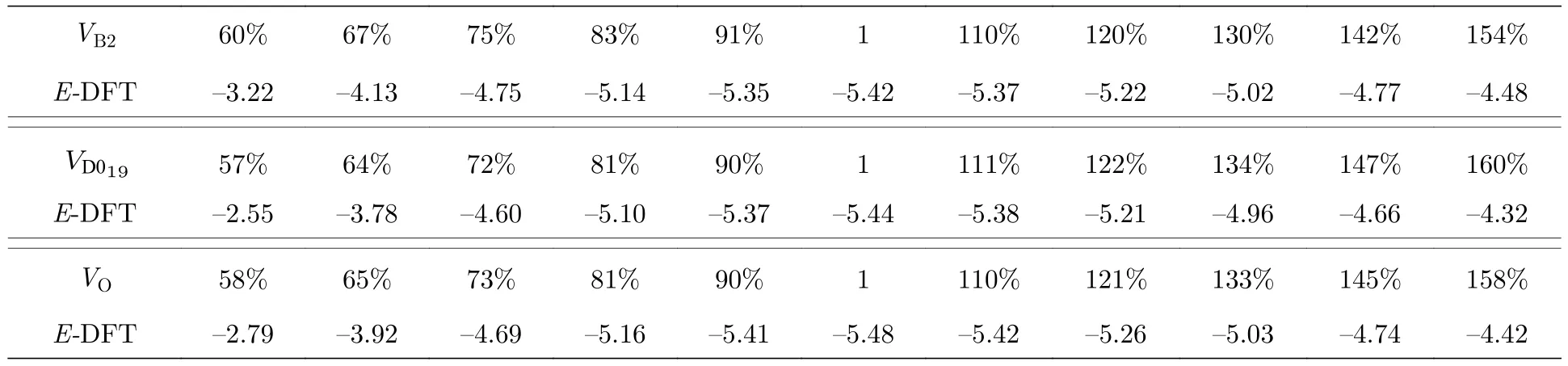
表8 Ti2AlNb 合金的內聚能(單位: eV)Table 8.Cohesive energies for Ti2AlNb alloys (in eV).

4 結論

本文使用傳統方法開發了Ti2AlNb 合金的EAM 勢.主要采用靜態計算和分子動力學模擬兩種手段考察了本文開發的EAM 勢的質量.

1) 靜態計算表明,該EAM 勢很好地再現了B2相Ti2AlNb 合金的彈性常數、內聚能和多種缺陷形成能,能很好地描述Ti2AlNb 合金B2 相、D019相、O 相的E-V系.其中B2 相的E-V關系在近距離約3.3 ?以內與Rose 曲線符合的非常好.

2) 利用Lammps 軟件模擬計算了B2-Ti2AlNb合金的各種空位形成能,計算結果均與第一原理計算結果符合得很好.置換原子形成能和換位原子形成能計算結果與第一原理結果相比,其大部分缺陷形成能的誤差均在0.100 eV 以下,對于Al 原子置換Ti 原子的置換原子形成能,誤差在0.165 eV 之內,Nb 原子置換Al 原子的置換原子形成能,誤差在0.233 eV 以內.利用Lammps 軟件模擬計算了B2 相Ti2AlNb 的表面能,計算結果表明B2 相的(110)面比(100)面更穩定,表面能更低,與第一原理的計算結果一致.

3) 利用Lammps 軟件模擬研究了Ti2AlNb 合金B2 相的熔化轉變過程,熔點的模擬結果大約為1400 K,低于實驗結果.主要由于開發勢函數的擬合庫中未包含與溫度、相變相關的物理量.

本文開發的Ti2AlNb 合金的EAM 勢在描述B2 相的彈性性能,點缺陷性能、表面能及E-V關系性能方面的能力較好,預測可用于與這些性能相關的力學性質方面的研究.