鈣鈦礦超晶格SrTiO3/BaTiO3 的撓曲電效應*

陳許敏 葉盼 王繼光 霍德璇 曹東興

1) (杭州電子科技大學理學院,杭州 310018)

2) (杭州電子科技大學電子信息學院,杭州 310018)

3) (杭州電子科技大學材料與環境工程院,杭州 310018)

4) (北京工業大學材料與制造學部,北京 100124)

撓曲電效應是應變梯度與電極化之間的機電耦合,存在尺寸效應,在許多微納米尺寸結構中起著非常重要的作用.本文采用密度泛函理論,對交錯層SrTiO3/BaTiO3 超晶格進行了系統的撓曲電效應研究,通過探究超晶格在給定的應變梯度下的力電響應,獨立得到其縱向撓曲電系數、橫向撓曲電系數和剪切撓曲電系數.結果表明: 超晶格的橫向、剪切撓曲電系數和縱向撓曲電系數較其組分材料有不同的變化,其中超晶格的橫向和剪切撓曲電系數分量分別較塊體BaTiO3 提升約6 倍,較塊體SrTiO3 提升4.2 倍和1.3 倍;縱向撓曲電系數較其組成材料基本不變;這種撓曲電系數分量不同程度提升的綜合效果能夠使超晶格SrTiO3/BaTiO3 較其單一組分材料的撓曲電效應產生數倍提升.本文對尋找性能優異的復合撓曲電材料具有一定理論指導意義.

1 引言

鈣鈦礦結構過渡金屬氧化物具有廣泛的物理特性,如鐵電性、鐵磁性、高溫超導和巨磁阻性等,是凝聚態物理和材料科學研究的熱點[1,2].應變梯度能夠破壞晶體的反演對稱性從而在材料中引起電極化,即撓曲電效應[3,4].撓曲電效應是材料應變梯度與電極化之間的耦合,不受材料對稱性和鐵電材料居里溫度等限制,僅依賴于材料的尺寸特征[5],在許多微納米尺寸結構中撓曲電效應對材料性質發揮主導作用[6].隨著對微納米材料的深入研究,ABO3型鈣鈦礦材料在小尺寸狀態下表現的撓曲電效應增強逐漸吸引了學者廣泛的關注[7].Lu等[8]通過原子力顯微鏡尖端在BaTiO3超薄膜中產生應力梯度來調節撓曲電極化,實現了采用純機械力動態切換控制極化.Wen等[9]提出了基于鐵基駐極體的撓曲電性駐極體,發現施加非均勻變形的情況下撓曲電性駐極體表現出巨大的撓曲電響應.

鈣鈦礦材料中存在多種可能影響撓曲電效應的因素,如內部微應變[10]、極性納米區域[11]和表面壓電性[12]等,都能很容易地對電極化產生影響,從而耦合到撓曲電效應中.表面壓電性的研究表明,表面/界面工程可能是控制和增強SrTiO3等材料的撓曲電性能的可行途徑[12].Zhang等[13]研究揭示了表面自發極化可能在塊體的鐵電材料中與撓曲電極化耦合,導致實驗上高估的撓曲電效應.因此,在實驗上測量所得到的撓曲電系數通常是多種因素的競爭組合結果.Zhang等[14]研究發現,LaAlO3/SrTiO3異質結以及Nb 摻雜的LaAlO3/SrTiO3異質結的撓曲電系數比LaAlO3,SrTiO3塊體單晶材料提升了若干數量級,并利用撓曲電效應在LaAlO3/SrTiO3的異質結構的界面實現調節材料的電子輸運性質.

利用異質界面引起的電荷、軌道、自旋以及晶格失配等自由度的重組逐漸成為調節材料電子結構的有力手段[15].氧化物超晶格將具有不同性質的材料耦合在一起,在氧化物超晶格中產生大量界面,放大了界面效應的可能性,從而影響超晶格應變下的電荷響應.Shu等[16]研究表明復合材料比一般塊體材料更容易存在顯著的撓曲電效應.隨著氧化物薄膜制備技術的飛速發展,制備具有原子尺度的鈣鈦礦過渡金屬氧化物超晶格成為現實[17].理論方面,學者們詳細研究了單晶材料的縱向、橫向和剪切撓曲電系數,包括BaTiO3和PbTiO3單晶材料的縱向撓曲電系數[18,19]和二者的橫向和剪切撓曲電系數[20];而超晶格材料的理論計算僅限于縱向撓曲電系數,如1SrTiO3/1PbTiO3(SPT)[15].目前,對鈣鈦礦超晶格材料的擾曲電效應綜合研究很少報道.本文通過構建由SrTiO3和BaTiO3以1∶1 的比例逐層交替的1SrTiO3/1BaTiO3(SBT)層狀超晶格材料,增加界面效應,采用第一性原理密度泛函理論 (density functional theory,DFT),研究超晶格在應變梯度下的極化響應,系統地計算和分析該超晶格材料的擾曲電效應,包括縱向撓曲電系數、橫向撓曲電系數和剪切撓曲電系數.為制備具有優異撓曲電性能的鈣鈦礦過渡金屬氧化物超晶格材料提供理論依據.

2 計算方法

本文采用基于DFT[21]的第一性原理計算軟件VASP(Viennaab initiosimulation package)[22],交換關聯勢使用廣義梯度近似 (generalized gradient approximation,GGA)的Perdew-Burke-Ernzerhof (PBE)泛函,電子-離子交換關聯作用采用投影綴加平面波勢處理[23],電子平面波函數截止能量為500 eV,自洽場迭代的能量收斂標準為1×10—5eV.布里淵區積分時,采用 Monkhorst-Pack的k網格[24],計算縱向和剪切擾曲電系數時采用6×6×1,計算橫向撓曲電系數時采用1×6×1.

撓曲電效應描述由四階張量相關的應變梯度引起的極化響應:

式中,Pi為撓曲電誘導的極化強度,為應變梯度,μijkl為撓曲電張量系數.根據撓曲電效應的定義可知,通過構造一個具有已知應變梯度的系統,然后計算由應變梯度誘導的極化強度,可以得到該體系的撓曲電系數.晶胞的極化強度是零電場條件下由應變梯度導致的原子位移極化,極化強度由玻恩有效電荷、晶胞體積和晶格中原子的相對位移決定:

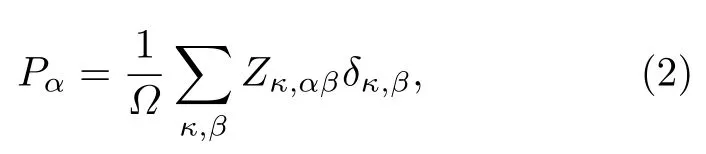
其中,Pα是沿著α方向的自發極化,Ω表示晶胞體積,Zκ,αβ是材料中原子的玻恩有效電荷,δκ,β是原子相對于中心對稱結構晶格的位移.

SrTiO3和 BaTiO3晶格參數如表1,超晶格系統模擬為SrTiO3和 BaTiO3交替生長的層狀材料,系統呈現1/1 層狀.計算模擬超晶格系統在SrTiO3襯底上沿(001)方向生長,因此,超晶格采用了 SrTiO3的面內晶格常數,并對超晶格的c/a進行了系統優化.

表1 結構晶格常數Table 1.Structural lattice constant.

3 計算結果與分析

3.1 縱向撓曲電系數

縱向撓曲電極化是z方向的應變梯度所引起的該方向上的極化,該極化和應變梯度的耦合關系式為

P3333是z方向的極化,?ε33/?z表示沿z方向的應變梯度,μ3333表示縱向撓曲電系數.圖1 給出了1×1×N(N為晶胞層數)縱向撓曲電超晶胞模型.圖1(a)是SrTiO3/BaTiO3的無應變超晶胞結構,該超晶胞模擬BaTiO3生長在基底為SrTiO3交替層排列的情形.考慮對圖1(a)所示的超晶胞結構施加沿Z方向周期性的應變:

其中ε(z) 表示坐標z處的應變值,h為超晶胞Z方向高度,εmax為最大應變.超晶胞原子沿Z方向的位移為

將(5)式形式的原子位移施加在圖1(a)所示的超晶胞結構中,即得到圖1(b)示意的內含應變梯度的SBT 超晶胞模型,晶胞內材料的應變梯度為

圖1 1×1×N 縱向撓曲電超晶胞模型 (a) 無應變;(b) 施加縱向應變Fig.1.1×1×N supercell model for longitudinal flexoelectricity: (a) Strain-free supercell;(b) supercell with longitudinal strain.

因此,建立了SBT 超晶格與應變梯度保持相同周期性的計算模型,如圖1(b)所示,在圖1(b)中余弦形式的應變分布使得h/4 和3h/4 位置的平均應變為零,壓電極化為零,消除了壓電效應對極化的貢獻,同時該位置晶胞的應變梯度最大,對應的撓曲電效應最大,可以提供最大的撓曲電極化.

為了使圖1(b)所示的超晶胞維持應變梯度的狀態,在施加應變ε33后,固定A位原子(Sr 或Ba)的位置,弛豫Ti 和O 原子到它們的平衡位置.對應變結構進行優化后,檢查未固定的原子位置,以查看松弛的超晶胞中是否仍然存在梯度應變.圖2 顯示了Z方向不同高度的超晶胞在εmax=0.5%情況下原子位移的分布情況,圖2(a)—(d)對應的晶胞層數N分別為12,16,20,24.圖2 表明弛豫后超晶胞中的余弦應變梯度仍然存在.通過圖2(a)可以看出,弛豫原子的位移比固定A位原子的位移小,意味著松弛原子的應變梯度小于預設的固定A位原子的應變梯度.而撓曲電系數由位移極化和應變梯度的比值得到,所以較小的梯度會導致高估的撓曲電系數.固定原子和弛豫原子的位移之間的差異在很大程度上是與超晶胞尺寸有關.圖2(b)—(d)顯示,隨著超晶胞尺寸逐漸變大,弛豫原子的應變梯度和受約束的A位原子的應變梯度之間的差異逐漸減小.圖2(c),(d)中顯示的超晶胞中原子間的應變梯度差異幾乎消失.間接表明,為了施加應變梯度而選擇約束A位原子是可靠的.這表明模擬計算時超晶胞的尺寸是影響撓曲電系數的一個重要原因.由此推測,隨著超晶胞尺寸的增大,晶格中固定原子和弛豫原子的應變梯度最終趨于一致,由N=24 情況下可以得到SrTiO3/BaTiO3超晶格的縱向撓曲電系數μ3333為—0.308 nC/m.

圖2 1×1×N 超晶胞中A 位原子和Ti,O 原子Z 方向的位移 (a) N=12;(b) N=16;(c) N=20;(d) N=24Fig.2.Atomic displacement along z direction in 1×1×N supercell: (a) N=12;(b) N=16;(c) N=20;(d) N=24.

3.2 橫向撓曲電系數計算模型

橫向撓曲電效應是X方向的應變引起沿Z方向上的極化,該極化和應變梯度的耦合關系式為

為了計算橫向撓曲電系數,構造了圖3(a)所示的M×1×N的超晶胞,M為超晶胞X方向的尺寸.為模擬計算橫向撓曲電效應,對圖3(a)中的超晶胞兩側對稱施加應變形式.如圖3(b)所示,該應變在X方向上關于藍色虛線軸對稱對稱分布,沿Z方向呈余弦式變化,且在X方向越靠近對稱軸,余弦形式的應變幅值越小,在對稱軸處為零,該應變表達式為

(8)式對應的原子位移表達式為

δ(x1)表示坐標為x1的原子在X方向的水平位移,x0表示圖3(b)所示的藍色對稱軸沿X方向的坐標.圖3(b)中超晶胞的應變梯度為

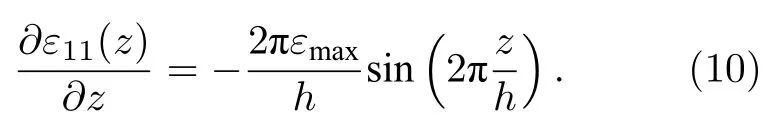
分析(8)式和(10)式可知,應變和應變梯度在Z方向上呈周期性,并且與超晶胞的周期一致.因此,橫向撓曲電效應引起的極化分布在Z方向也是周期性的且在邊界處連續,從而可以減小退極化場的影響.為了保持弛豫前后晶胞單元在X方向上的總長度不變,固定超晶胞兩側邊緣的原子,以保持超晶胞體積保持不變.

圖3 M×1×N 的橫向撓曲電超晶胞模型 (a) 無應變;(b) 施加橫向應變Fig.3.M×1×N supercell model for transverse flexoelectricity: (a) Strain-free supercell;(b) supercell with transverse strain.

為保持圖3(b)所示超晶胞內的應變,在施加應變ε11(z) 后,固定Ba,Sr 原子在X方向的坐標,但允許在其他兩個方向弛豫;Ti 原子和O 原子不受約束,可以在各個方向弛豫.結構優化后,超晶胞Y方向上的原子沒有發生應變,即ε22=0.對Z方向的晶胞沒有限制,表明晶胞中原子可以在Z方向上自由弛豫.原子弛豫到它們的平衡位置時,(10)式的應變梯度仍然存在于超晶胞中內部.選取超晶胞中對稱軸上的晶胞來考慮撓曲電系數,因為此處的晶胞受水平方向上對稱的應變,能消除水平退極化場的影響.對于SrTiO3/BaTiO3超晶格,極化也可能通過壓電效應產生,為了準確計算橫向撓曲電系數,需盡可能消除壓電效應的影響.根據(8)式,位于超晶胞中間列h/4 和3h/4 位置的晶胞水平應變為零,不受壓電效應的影響,同時從(10)式可知,此處的應變梯度最大,撓曲電效應最大.因此,選擇超晶胞中間列h/4 和3h/4 處的晶胞來計算橫向撓曲電極化強度,不僅可以消除壓電貢獻,而且由于其最大的應變梯度而具有最大的撓曲電性.

對施加了應變的M×1×N超晶胞進行結構優化,最大應變設置為εmax=0.5%.經過測試,為維持超晶胞應變梯度的存在,設置M=7 比較合適.圖4(a)—(c)是超晶胞在不同縱向尺寸下的原子水平位移,在Z方向上單胞層數分別為N=8,12,16.圖4 顯示了超晶胞結構優化后O 原子弛豫到趨于固定原子的應變狀態,證明了結構優化后的超晶胞處于應變梯度狀態.

從圖4(a)可以看出,弛豫后晶胞內O 原子的位移分布呈余弦形式,但與固定A位原子的位移差異明顯.隨著超晶胞縱向尺寸的增加,圖4(b)中的固定原子和非固定原子之間的差異進一步減小.圖4(c)中O 原子的位移曲線幾乎收斂到與Ba/Sr的位移曲線相一致.在h/4 和3h/4 的特定位置,Sr/Ba 原子位移曲線和O 原子的位移曲線相交且Z方向的位移基本為0,如圖4(c)中的第4 個和第5 個紅點(從左到右)所示.因此,如果我們選擇這些特定的位置來計算超晶胞的撓曲電系數,就可以忽略壓電效應的影響.由于超晶胞內周期性位移分布,以及垂直極化沿z方向的連續性,使其在超晶胞的頂部和底部邊界沒有退極化場,同時中間一列晶胞不受水平去極化場影響.因此,超晶胞尺寸的變化,并不會引起退極化場對撓曲電系數的影響.

圖4(d)中的實線對應于圖4(c)N=16 時的縱向應變分布以及撓曲電極化分布.可以看出,對超晶胞在X方向上施加的橫向應變梯度,導致中間列的單晶胞在Z方向發生余弦形式的應變分布,這意味著沿Z方向存在縱向應變梯度及其誘導的縱向撓曲電極化.因此,模擬計算橫向撓曲電系數時,SrTiO3/BaTiO3超晶胞的總撓曲電位移極化包括橫向撓曲電極化和縱向撓曲電極化的貢獻,總撓曲電極化可表示為

其中,P0是初始狀態的自發極化,對于非鐵電晶體,P0=0.(11)式中由應變梯度誘導的位移極化可以根據玻恩有效電荷計算得到.根據(11)式計算得到超晶胞中間一列的撓曲電極化情況,如圖4(d)中的虛線所示,是N=16 的超晶胞的極化分布.可以看出,h/4 和3h/4 處的局部極化強度達到最大且方向相反.

圖4 7 ×1×N 超晶胞中A 位原子和O 原子的Z 方向位移 (a) N=8;(b) N=12;(c) N=16;(d) N=16 超晶胞中的撓曲電極化分布和縱向應變分布Fig.4.Z displacement of A-atoms and O-atoms in 7 ×1×N supercell: (a) N=8;(b) N=12;(c) N=16;(d) the polarization and longitudinal strain along z direction with N=16.

由于撓曲電極化中包含橫向撓曲電極化和縱向撓曲電極化兩種成分,為了準確測量橫向撓曲電系數,需要消除縱向撓曲電極化的貢獻.由橫向應變引起的縱向撓曲電效應可以根據縱向應變梯度和縱向撓曲電系數的耦合得到,其中縱向應變梯度可以根據圖4(a)中的應變分布得到,縱向撓曲電系數由前文的計算結果得到,這里取μ3333=—0.308 nC/m.根據(11)式,橫向撓曲電系數計算如下:

在圖4(d)中最大撓曲電極化的位置計算得到的橫向撓曲電系數μ3311=9.87 nC/m.

3.3 剪切撓曲電系數

剪切撓曲電效應指沿Z方向變化的X方向的應變引起的X方向上的極化,該極化和應變梯度的耦合關系用下式描述:

根據剪切撓曲電效應的定義構造了一個計算剪切撓曲電系數的超晶胞,如圖5(a)所示,對此超晶胞施加了沿豎直方向余弦變化的水平位移,該位移表達式為

其中,γ是剪切應變的比例因子.圖5(b)為施加剪切應變后的超晶胞模型,由于原子的水平位移很小,對(12)式做二階求導得到超晶胞剪切應變梯度表達式為

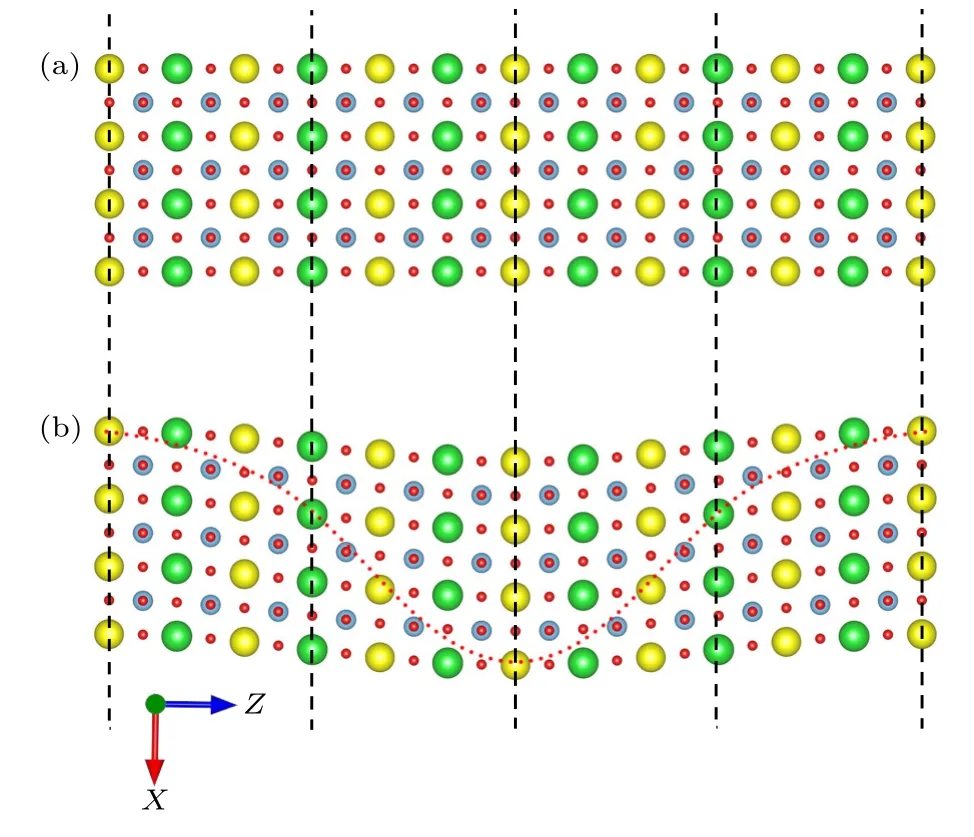
圖5 M×1×N 的剪切超晶胞模型 (a) 無應變模型;(b) 施加剪切應變Fig.5.M×1×N supercell mode for shear flexoelectricity:(a) Strain-free supercell;(b) supercell with shear strain.

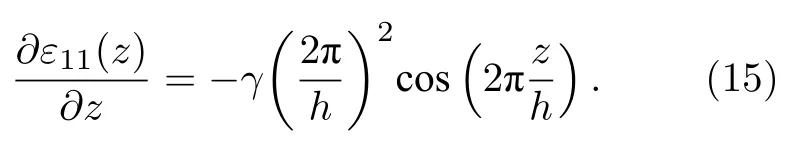
對施加剪切應變后的超晶胞進行結構弛豫,Ba/Sr原子X方向坐標在弛豫過程中固定,其他原子各方向坐標允許弛豫到其平衡位置.

為了研究超晶胞的剪切撓曲電效應,對不同縱向尺寸的剪切應變超晶胞模型進行了結構優化,剪切應變系數γ=0.3 ? (1 ?=10—10m).弛豫超晶胞結構后,考察不同尺寸的超晶胞中應變梯度是否存在.圖6(a)—(c)給出了超晶胞中Sr/Ba 原子和O 原子位移的比較.結果表明,在圖6(a)中,對于較小的縱向尺寸(N=12),O 原子的位移并不收斂于固定Sr 原子位置的位移.當尺寸增加到N=28時,Sr 和O 原子的位置保持一致,如圖6(c)所示,這表明隨著晶胞尺寸增大,結構弛豫后超晶胞內固定原子與非固定原子最終能夠維持預計的應變梯度.

對于沒有壓電效應和自發極化材料,對極化的唯一貢獻來自剪切撓曲電效應.利用玻恩有效電荷計算超晶胞中的水平撓曲電極化,圖6(d)顯示了N=28 的超晶胞中的水平極化隨Z高度的分布.可以看出,局域極化的分布與(15)式給出的應變梯度方程具有相同形式,呈余弦形式變化.從圖6(a)—(c)可以看出,h/2 晶胞位置處應變梯度最大,撓曲電效應最強,因此在h/2 晶胞位置來計算超晶格的剪切撓曲電系數.根據(13)式計算在應變梯度最大的方向上的剪切撓曲電系數μ1313,當N=28 時,μ1313=—9.02 nC·m—1.

圖6 3×1×N 超晶胞中A 位原子和O 原子的X 方向位移情況 (a) N=12;(b) N=16;(c) N=28;(d) N=28 超晶胞中不同高度的X 方向極化Fig.6.X displacement of A-atoms and O-atoms in 3 ×1×N supercell: (a) N=12;(b) N=16;(c) N=28;(d) X-polarization at various height inside supercell with N=28.

3.4 結果討論與分析

表2 總結了不同塊體材料和超晶格的撓曲電系數理論計算值.塊體BaTiO3,SrTiO3,超晶格SBT 的橫向撓曲電系數和剪切撓曲電系數均為nC/m 量級,對應的縱向撓曲電系數為次nC/m 量級.然而,SBT 超晶格的橫向和剪切撓曲電系數相比于組成材料 BaTiO3和 SrTiO3都得到了數倍的增加;其中,SBT 超晶格的橫向、剪切撓曲電系數分量較塊體 BaTiO3提升約6 倍;較塊體 SrTiO3橫向和剪切撓曲電系數分別提升4.2 倍和1.3 倍.縱向、橫向和剪切撓曲電系數的綜合效果將決定SBT 超晶格在實驗上的擾曲電性能.SBT 超晶格材料在外界的應變梯度下在豎直方向產生的撓曲電場應當表示為[8]

表2 撓曲電系數匯總Table 2.Summary of flexoelectric coefficient.

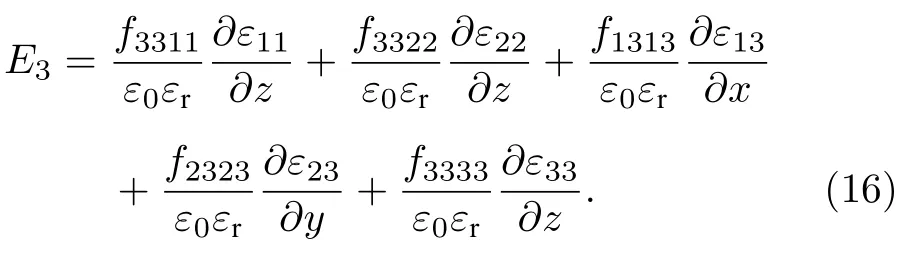
其中,E3是豎直方向的撓曲電場,ε0是真空介電常數,εr是應變下的介電常數,等號右邊第一項和第二項是橫向撓曲電效應的結果,第三項和第四項是剪切撓曲電效應的結果,最后一項是縱向撓曲電效應的結果.在SBT 結構中,橫向和剪切撓曲電分量的增強對總體的撓曲電效應增強有顯著效果.因此,SBT 超晶格理論上可以擁有數倍于塊體組成材料的擾曲電性能.

SBT 超晶格的縱向撓曲電系數略微減小,與Hong[18]和Xu等[20]計算的塊體鈣鈦礦材料 BaTiO3的撓曲電系數有相同的數量級.一方面,可能是由于 SrTiO3和 BaTiO3晶格失配影響原子在c方向的位移,導致高估的應變梯度從而低估了撓曲電系數.另一方面,可能是由于原子堆垛順序對極化產生影響,不同的原子堆垛順序會有不同的界面結構.Guo等[25]研究發現,在 SrTiO3/BaTiO3異質結中,TiO2-BaO 界面結構產生的界面效應會削弱縱向撓曲電極化,SrO-TiO2界面效應會增強縱向撓曲電極化,此外,不同堆垛順序異質結構的界面結合能表現出顯著差異,這種堆疊次序對縱向撓曲電極化的影響仍需進一步確認.

4 結論

超晶格鈣鈦礦氧化物豐富的界面行為使其可能表現出優異的撓曲電性能.本文構建了鈣鈦礦氧化物超晶格SBT,采用第一性原理計算了在給定的應變梯度下,超晶格中的原子位移,結合玻恩有效電荷,得到撓曲電極化與應變梯度的耦合關系,即撓曲電系數.通過構建超晶格的方式向材料中引入更多界面,顯著提升了材料的橫向和剪切撓曲電系數,是一種增強撓曲電效應的可靠思路,系統且全面地豐富了撓曲電效應在超晶格中的研究,為撓曲電系數的實驗測量提供參考.同時,為獲取較大撓曲電系數材料提供了一種可能的方法,即通過組成交錯結構的超晶格材料來調節撓曲電性器件的撓曲電響應,為尋找和制備高性能的撓曲電材料提供了新思路.