自適應階次跟蹤技術在走行部故障診斷中的應用

包學海，孔繁鵬，謝燁，水沛，尹旭曄

（1.浙江杭海城際鐵路有限公司 工程管理部，浙江 杭州 310000；2.中鐵信（北京）網絡技術研究院有限公司 技術開發部，北京 100000；3.浙江省交通投資集團有限公司 智慧交通研究分公司，浙江 杭州 310000；4.浙江中自慶安新能源技術有限公司 產品部，浙江 杭州 310000）

1 概述

城市軌道交通作為一種運能大、速度快、安全準時、能源節約、環境友好的交通方式，逐漸成為城市公共交通的骨干，是大中城市解決交通問題的首選交通方式。據中國城市軌道交通協會統計，截至2019年12月31日，我國共有40座城市開通運營軌道交通列車，運營里程合計約6 730 km。目前，城市軌道交通列車維修模式多以計劃性維修為主，即按運行公里或時間間隔進行定期維護或維修。走行部作為列車重要的系統之一，其工作狀態直接影響列車運行安全。針對走行部軸箱軸承、齒輪箱、電機等旋轉部件，通過人工“耳聽目測”檢查方式難以判斷出部件故障，尤其針對一些早期故障及隱患不能及時判斷和預警，列車的運行安全受到嚴重威脅。

在變轉速轉子故障診斷方面，唐貴基等［1］提出一種基于SSD-HT時頻階次跟蹤的轉子故障診斷方法。楊炯明等［2］在階次分析中引入瞬時頻率理論，研制出虛擬式旋轉機械特征分析儀。Borghesani等［3］提出一種新的基于速度同步的離散傅里葉變換，提高了計算階次跟蹤的分析效果。Wu等［4］基于遞推最小二乘（RLS）濾波的階次跟蹤算法對振動信號和聲發射信號進行特性分析和試驗比較。Pan等［5-6］提出一種可調諧加權因子，用于有效區分和分離旋轉機械測量信號的閉合和交叉階分量。Wang等［7］采用多種階次跟蹤技術對變速諧波振動去噪，強調包含裂紋信息的非階數相關振動，論證了階次跟蹤技術在轉子裂紋檢測中的優越性。Wu等［8］通過自適應階次跟蹤技術提取階次特征作為神經網絡輸入，提出利用網絡開發故障診斷系統的人工神經網絡技術。張程鵬等［9］通過Compact RIO階次跟蹤和信號包絡提取技術相結合的方法，分析風力發電機組齒輪箱變速過程中振動信號非平穩的特點。在滾動軸承［10-15］和齒輪箱［16-20］的故障診斷方面，通過階次跟蹤有效識別和提取到變轉速工況下非平穩特征信號，有效識別出非常接近的和微弱的振動特征成分，從而成功地檢測出不同類型的齒輪故障。

從以上研究現狀看，故障診斷技術只經歷了短短幾十年的發展，但已經在城市軌道交通列車的軸承、輪對車軸齒輪箱和踏面等的監測診斷方面得到了長足發展和廣泛應用。基于列車啟停頻繁、車速快、車輪高速旋轉和受力集中等特點，走行部的部件長期處于摩擦、沖擊、振動、腐蝕等自然損耗狀態，一旦出現故障，會影響列車的安全性和穩定性，甚至危及乘客生命財產安全。

近年來，走行部在線檢測和故障診斷技術快速發展，基于廣義共振和共振解調的故障診斷技術在走行部旋轉部件故障診斷中得到廣泛應用，如岳曉峰等［21］研究團隊發表的研究成果。但這些研究成果通常會預設一個二次或多次的列車行為模式，由于列車運行速度隨時間變化，運行速度直接取決于車輪的旋轉角速度，故其特征頻率和故障頻率也會隨列車的運行速度一同變化，如果采用基于固定時間間隔采樣的傳統信號采樣策略，采集到的故障信號頻率不是某一個具體值，而是由列車運行速度決定的范圍，同時信號能量會分散在此范圍，進而導致故障信號的頻率范圍模糊且信號強度降低。以列車運行規律固定為前提的階次跟蹤，因為走行部軸承、齒輪及車輪等旋轉部件時變工況下振動信號非平穩特點，在實際運用中存在一些不足。

針對此不足，根據城市軌道交通列車啟動、加速、減速、停車等頻繁啟停特點，基于階次跟蹤技術對杭海城際列車走行部的車輪進行振動監測，采集某一時間段內運行數據，通過最小二乘法擬合出車輪角度增量和時間增量之間的關系，引入振動信號，通過傳統FFT（Fast Fourier Transformation）和階次跟蹤的方法，得到等時間步長和等角度步長的頻譜圖，進行對比分析，證明階次跟蹤可有效避免列車行駛過程中由于變速導致的信號采樣模糊問題，是一種可靠的列車走行部旋轉部件故障診斷技術。

2 基本理論

2.1 階次跟蹤技術

階次跟蹤技術（Computed Order Tracking，COT）是旋轉機械非平穩振動信號處理的重要技術之一。對于變轉速旋轉機械設備（包括牽引電機軸承、齒輪箱軸承等）的故障診斷，相對于參考軸或鍵相信號進行等角度增量采樣時，雖然此信號在時域上是非穩定信號，在角域上卻是穩定信號，對角域上的穩定信號進行譜分析便可得到清晰的圖譜，即階比譜。因此，振動信號表示為：

式中：A(θ)為轉過角度θ的振動信號幅值；Am為階次為m的諧波分量幅值（其中，m=1，2，3，…）。

階次、頻率、轉速之間的關系為：

式中：f為觀測對象的頻率，Hz；n為參考軸的轉速，r/min。

對于行駛過程中列車的角度增量為：

式中：θ(t)為t時刻的角度增量，（°）；L(t)為t時刻列車的行駛位移，m；r為列車車輪的半徑，mm。

岳曉峰等［21］研究階次跟蹤在變速箱故障診斷中的應用時，假設變速箱轉軸的運動模式為勻加速運動。實際工程中，轉軸的運動往往較復雜［22-24］，所以考慮更復雜的勻變加速運動，列車的行駛位移L表示為：

在時域信號中，設鍵相脈沖的角度增量為Δθ，任意4個相鄰時刻(t1，t2，t3，t4)，將其代入式(4)中構成數據矩陣為：

從而求得a，b，c，d的值，回代到式(4)即可求得Δθ和t的關系。

2.2 采樣插值和擬合

采樣時間間隔決定采樣精度，由于實際采集數據過程中，采樣結果為離散點，為提高計算精度，更接近實際振動，常采用插值的方式實現離散函數逼近，以滿足給定約束。如同采樣時間間隔精度一樣，插值方法的精度同樣決定重采樣的幅值精度。

假設在車輪某一部位布置鍵相標記k，對以上采集的數據進行等角度重采樣，采樣時，其角度增量Δθk為2π的整數倍，即：

通過最小二乘法擬合出Δθk與tk的關系，在[iΔθ，(i+1)Δθ]之間進行等角度細化，即等角度采樣的鍵相序列θkm，km=1，2，3，…，M，（M為階次跟蹤的信號長度，即單次分析的采樣點數）。

以勻變加速度為例，假設原始信號為：

通過最小二乘法對θ與t的關系分別進行二次和三次多項式擬合，并進行階次跟蹤得到的關系見圖1。

圖1 不同擬合關系對階次跟蹤的影響

從以上不同擬合關系得到的階次跟蹤結果可以看出：相比于二次多項式擬合，三次多項式擬合由于和原始信號階次相同，以該方式擬合后的階次跟蹤更清晰地呈現出振動頻率，具有更好的階次跟蹤效果和更高的分析精度。

為提高擬合近似度，可以采用線性插值的方法，對采樣的角度間隔進行細化。對式(7)進行線性插值后，分析得到的階比譜存在一定底噪，這是由于插值方法的階次跟蹤信號無法完美重現原本的信號，導致出現了噪聲，該噪聲具有的頻帶寬度遠遠大于它作用系統的帶寬，并且在該帶寬中其頻譜密度基本可以作為常數考慮，因此，把它當作白噪聲處理。

對式(7)中的信號分別進行等時間采樣和等角度采樣，0～5 s和59～60 s時間段內2種采樣方式的對比結果見圖2，從圖2（a）可以看出，0～5 s時間段內，由于轉速較小，等時間步長采樣結果優于等角度采樣結果，擬合曲線更接近于原始信號；隨加速度不斷變化，轉速隨之不斷變化，在59～60 s時間段內，等角度采樣精度明顯優于等時間采樣精度。因此，對于變轉速運動，采用等角度采樣更能得到接近于實際振動的信號［25-26］。

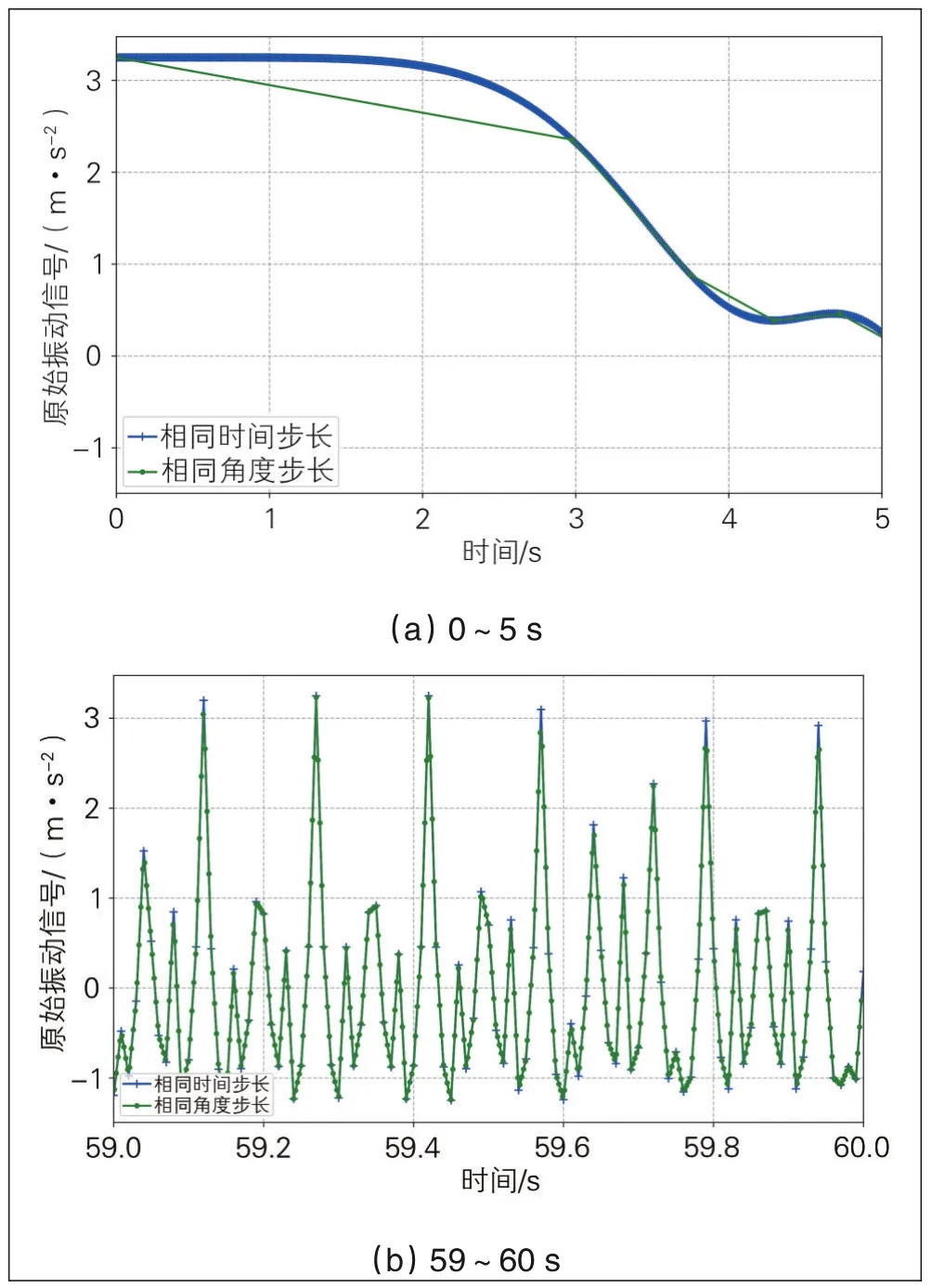
圖2 等時間步長和等角度步長采樣對比

3 自適應階次跟蹤技術在杭海城際列車的應用

3.1 運行數據實地測量

以齒輪箱這一走行部中最具代表性的旋轉部件為研究對象，杭海城際線路采用B型城際列車，其走行部齒輪箱的傳動比為117/22，具體參數見表1。實際運行時，對列車運行時轉向架各部件的信號均進行分析，以齒輪箱輸出軸前軸承的振動幅值信號為研究對象。

表1 杭海城際列車走行部齒輪箱參數

在列車運行某一時間段內進行等時間采樣，采樣頻率為100Hz。列車行駛過程中加速度與時間的關系見圖3。

圖3 列車行駛過程中加速度與時間的關系

從圖3中可以看出，列車在行駛過程中，加速度時刻發生變化，0～30 s時間段內，加速度值近似為0，可以看作勻速運動，35～60 s和60～80 s這2個時間段可以看成加速度增量不同的2段勻變加速運動。為使分析結果更接近實際工況，通過對已有測量數據插值的方式，重新構建等角度間隔的數據集。

引入仿真振動信號模型，模型參數見表2。

表2 仿真振動信號模型參數

3.2 運行模式自適應

圖3描述典型的列車勻速穩定運行—剎車—再啟動—勻速穩定運行過程，基于圖3運動狀態、表1提供的振動信號，分別進行時間FFT和階次跟蹤，得到的等時間步長頻譜見圖4。圖4（a）中頻率成分繁復雜亂，由于振動信號中的振動頻率隨時間不斷變化，該信號屬于非穩定信號，每次執行單一的FFT變換，僅通過改變窗函數大小和形狀進行分析，只能處理變化規律恒定的信號，很難適應隨時變化的信號，得到譜線反映的是窗內所有頻率成分，因此，無法識別故障頻率的特征；為更好地接近原始信號，用三次多項式進行擬合，并進行階次跟蹤得到的階次跟蹤頻譜見圖4（b），從結果看，對等時間采樣的信號，采用階次跟蹤得到的階比譜中頻率模糊，依然不能清晰呈現故障特征。

圖4 等時間步長頻譜

階次跟蹤與FFT變換的區別在于分析域不同，階次跟蹤將FFT變換的等時間采樣轉換為等角度重采樣。對原始振動信號在角度域上重采樣，可大幅提高分析頻率的精度，以及在后續分析中的準確性。運用最小二乘法擬合出Δθk與tk的關系，在[iΔθ，(i+1)Δθ]之間進行等角度細化，在每個鍵相之間通過線性插值的方法插入10個值，得到θ與t的近似關系。通過對列車振動信號的擬合和等角度鍵相插值，得到角度鍵相和時間序列的關系。隨時間變化，角度鍵相的稀疏程度發生變化，加速度為正時，速度不斷增加，等時間間隔內，角度鍵相分布稠密；反之，分布稀疏。在70 s左右時，列車運行速度最小，車輪的轉動角速度也最小，等時間間隔內，角度鍵相最稀疏。

通過等角度重采樣和等角度鍵相間線性插值，得到重采樣信號并進行階次跟蹤，得到的階次頻譜見圖5，圖中可以清晰地看到階次分別為1、2、4、6、8的諧波成分，與仿真的振動信號頻率成分吻合。對于變轉速運行的復雜工況，階次跟蹤可有效避免等時間采樣導致的采樣模糊、故障頻率的頻率范圍模糊且信號強度低等問題。

圖5 階次頻譜

3.3 運用小結

在杭海城際列車的走行部在線監測系統中，同時采集時域信號和階次跟蹤信號，用于對比不同故障在列車不同運行狀態下的不同表征。在對比過程中，可以清晰地看到對于典型的列車啟停過程，基于多項式擬合的階次跟蹤難以準確得知故障頻率，使用提出的自適應階次跟蹤技術，可以更準確地捕捉到故障信息。

4 結束語

城市軌道交通列車啟停頻繁、車速變化繁雜，但車輪的行駛速度始終取決于車輪的旋轉角速度。在高速旋轉且受力集中的情況下，基于等時間采樣的振動信號，信號能量分布于與列車行駛速度相關的范圍內，即故障頻率將分散于某一頻域范圍，不能準確得知故障頻率和故障原因。

采用自適應階次跟蹤技術時，通過等角度采樣的方式，自適應調整采樣頻率，將時域上的非穩定信號轉化為角域上的穩定信號，通過階次跟蹤得到階比譜，可以清晰地看出階次諧波成分，精確地識別故障頻率。

常見的階次跟蹤技術需要預先假設一個二次或者多次的關系對設備運行規律進行擬合，一旦設備的運行規律較復雜，則難以準確進行階次跟蹤。使用自適應階次跟蹤技術可以適應設備各種復雜的運行模式，在城市軌道交通列車走行部旋轉部件實際監測運用中可以更好地捕捉到設備和故障特征，使階次跟蹤技術在城市軌道交通列車故障診斷中具有更廣闊的應用前景。