基于啟發式算法的乏燃料裝料排期計劃研究

蘇 康，黎知行，史 驥，李仕元，景順平

［1.中廣核（北京）仿真技術有限公司，深圳 518031；2.中廣核鈾業發展有限公司公司，北京 100029］

我國商用核電站乏燃料的去向一般為離堆干式貯存或后處理。傳統乏燃料運輸方式是單起點與單終點“門到門”的公路運輸，單批次運輸2～3個貨包。隨著核電站增多，原有的運輸模式已不能適應當前乏燃料離堆的緊迫性需求。近年來我國開展了乏燃料多式聯運建設，單批次最大運輸量提升到10個貨包，傳統公路運輸單批次運輸模式對裝料排期的要求尚不明顯，然而在乏燃料多機組多式聯運時，裝料排期計劃的合理性尤為重要。

基于乏燃料多式聯運單批次運輸10個貨包，以及多核電基地、多臺機組和多個作業面同步裝料等狀況，通過統籌考慮各核電站乏燃料的外運緊迫性，并根據后處理設施的能力與容器資源進行動態調度，以實現乏燃料處理能力的進一步提升。

高級計劃排程（Advanced Planning and Scheduling，APS）理論是對實際業務邏輯進行抽象建模，以實現對計劃的制定與調度。文獻［1］報道，劉海江等研究APS與傳統能力需求計劃（Capacity Requirement Planning，CRP）的能力需求分析比較，發現APS具有整體規劃、計劃優化和實時性這三個技術特點；Rudber分析了APS的實施對鋼鐵加工公司戰術計劃水平的影響［2］；Romero研究了批量化學加工行業中和財務管理有關的計劃和排程問題［3］；張騰飛等利用APS系統解決了車間作業調度問題，重點是運用改進遺傳算法來解決經典的作業調度和柔性作業調度問題，并驗證了算法的性能［4］；吳雁等提出了一種基于制造執行系統（ManufacturingExecution System，MES）的機加高級計劃排程的應用框架，并通過實際的應用案例來驗證該框架［5］；肖牧山等提出了基于約束理論（Theory of Constraints，TOC）和鼓-緩沖 -繩（Drum-Buffer-Rope，DBR）模型的APS系統與企業資源計劃（Enterprise Resource Planning，ERP）集成的解決方案，并給出了APS與ERP集成的潛在問題和可行方案［6］；沈潔鋒等對乏燃料的管理方式以及我國乏燃料管理的現狀進行了分析討論［9］；李曉娟等利用信息技術、物聯網和大數據等技術手段，通過提升設備智能化水平完善運輸保障，搭建智能化監管平臺和應急響應平臺以實現全過程的可視化監管和快速反應上報等，保障危險品的安全運輸［7］。涉及乏燃料調度體系的研究鮮少，故劉群等認為需要建立乏燃料調度體系，以實現各環節的高效調度與統籌協調［8］。

綜上所述，在APS的應用和研究方面，APS理論多應用于生產制造領域，尚未用于乏燃料運輸領域。本文根據乏燃料運輸計劃的特點，基于運輸計劃的業務邏輯，應用APS理論，建立了混合整數規劃模型，并兼顧模型的規模與未來的拓展性，設計了一種啟發式算法實現加快模型求解過程。

1 基于資源約束的APS模型

在單次運輸計劃中，裝料環節耗時長，在整個周期中占比大，且各機組的裝料時間窗不同，故裝料排期計劃不同導致裝料完工時間不同。裝料環節按各電站內其機組的外運緊迫性，以及各機組的裝料時間窗、容器數量上限和各后處理廠的卸料時間窗等約束條件，對多臺機組進行空容器分配，并兼顧單個貨包裝載高燃耗組件至卸料全過程低于6個月的前提下，以期使裝料完工時間最短。

1.1 模型假設

（1）各機組有多個不可裝料時間窗；

（2）不考慮總成本變化；

（3）不考慮電站間空閑作業面調度分配；

（4）不考慮裝/卸空容器時間；

（5）所有容器的容量相同；

（6）單個容器裝/卸料時間為11/15 d；

（7）換裝、海運和鐵運時間均為固定標準時間；

（8）每個電站最少配置1套作業面（1輛公路運輸車和裝/卸料專業設備等）；

（9）裝料無搶占性，即不允許任意作業面的裝料插入另一作業面的裝料過程中；

（10）各機組裝料任務必須連續作業。

1.2 參數和變量

本文涉及的參數和符號如表1所示。

表1 符號說明Table 1 Parameter description

1.3 數學模型

乏燃料裝料排期計劃涉及裝料任務完成時間優先和外運緊迫性優先兩個目標。

裝料任務完成時間目標：

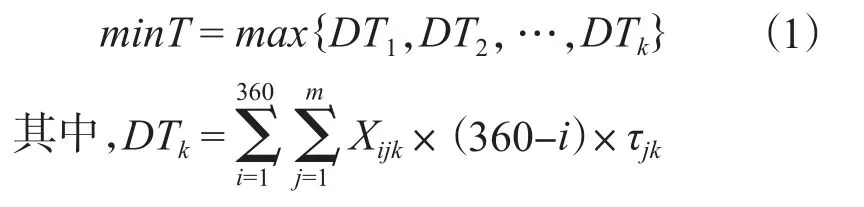
外運緊迫性目標：

其中，wij=Cij/Lij

將不同目標歸一化后采用加權的方法求解。時間目標是求解單個作業面的最大完工時間，外運緊迫性目標是求解所有機組外運緊迫性的最高值，因此將單目標設為最大值函數。考慮到實際場景中兩者的相對重要程度，將早期的時間設置更高的權重，使裝料計劃被提前執行，以節省總體裝料時間，降低計劃的完成時間。確定的目標函數如式（3）所示。

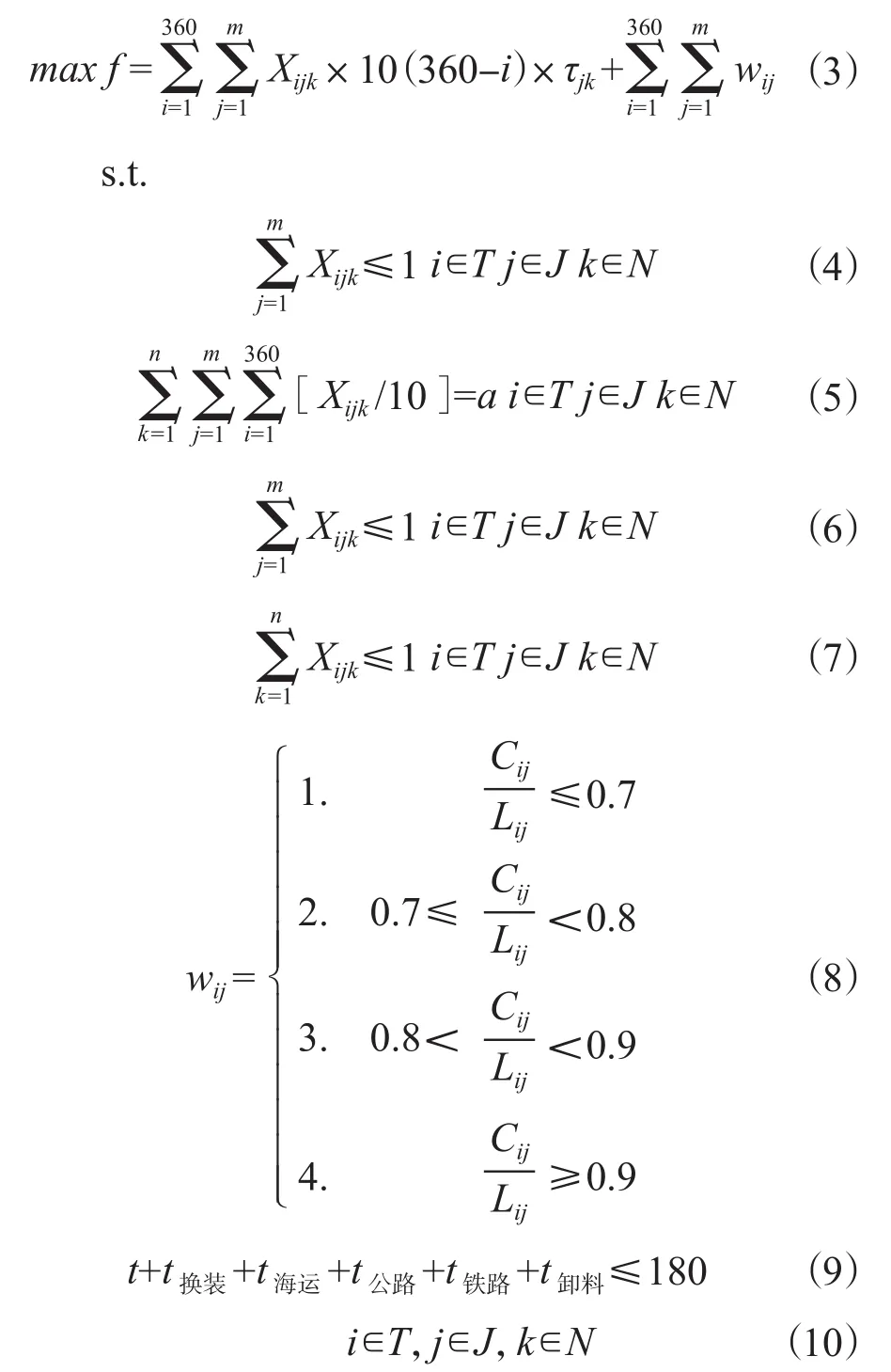
其中：

公式（1）為時間目標，即最小化最大完工時間，指從第一個機組裝料開始時間到最后一個機組卸料完成所耗時間的最小化；

公式（2）為外運緊迫性優化目標，即優先到外運緊迫性高的機組裝料；

公式（3）為多目標歸一化后的目標函數，即在滿足盡早開始裝料時間的前提下，外運緊迫性高的機組優先開始裝料；

公式（4）表示每個機組每次分配容器上限，即第j個機組最多分配μj個容器次；

公式（5）表示總分配容器次數量上限，即各機組分配容器次等于目前擁有的容器次；

公式（6）表示作業面數量上限，即同一時刻i、同一作業面k下，只能存在一個機組j裝料；

公式（7）表示單機組不可同時裝多個容器，即同一時刻i、同一機組j下，只能存在一個作業面k進行裝料；

公式（8）表示外運緊迫性約束，根據各機組存量占比將外運緊迫性進行分級處理；

公式（9）表示總運輸完成時間滿足時長約束；

公式（10）為變量取值約束。

2 算法設計

整個運輸計劃的裝料排期問題本質上屬于車輛路徑問題（Vehicle Routing Problem，VRP），而VRP是典型的非確定性多項式難題（nondeterministic polynomial hard，NP-hard），故裝料排期計劃也屬于NP-hard問題。

本文建立的模型中既有連續變量又有整數變量，為混合整數規劃模型。從可拓展可推廣的角度出發，設計基于優先規則的啟發式算法來求解該問題。其求解流程如圖1所示。

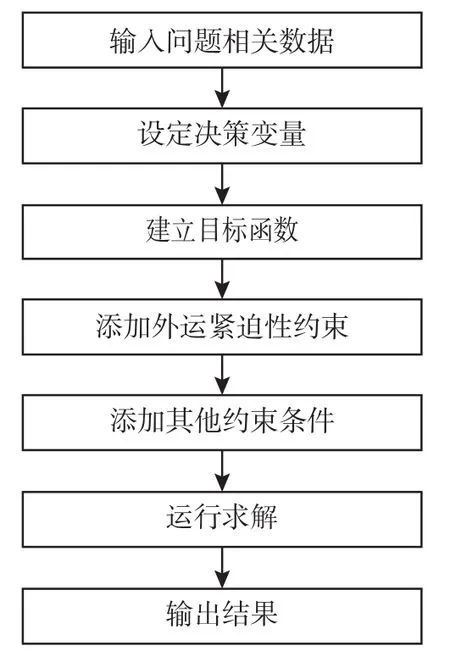
圖1 求解流程Table 1 Solve loop

首先根據單次計劃需要處理的乏燃料數量，確定需要使用的總空容器的數量；然后基于一定的分配策略將空容器分配到各機組，及時運走對應機組燃料池中的乏燃料，使得各機組能夠穩定安全運行。

當單次計劃需要處理的乏燃料數量不同時，需要使用的空容器數量也不同。對于分配策略的選擇，既可依各機組外運緊迫性的大小排序，亦可任意分配，以尋找單次運輸計劃用時最短的分配方案，并要滿足各機組緊迫性的上下限。

根據緊迫性大小排序進行分配，人工干預的程度較大，找到的方案與最優解的距離較大。如果任意分配，當需要使用的空容器數量比較多時，計算成本較大，需要由代碼的執行效率決定。本文采取上述二者之間折中的方案，具體步驟如下：

Step1：輸入數據和相關參數。

Step2：隨機生成各組件狀態信息，根據組件狀態分析各機組組件的最小冷卻時間，以及在裝料計劃開始時間時是否完成冷卻。

Step3：基于各組件完成冷卻時間確定計劃開始時間時各機組的最大可外運量。

Step4：加入各機組的不可裝料時間窗和后處理廠的卸料時間窗。

Step5：創建模型，加入外運緊迫性權重，建立多目標歸一化的總運輸時間最小化目標函數。

Step6：添加各項約束條件。

Step7：設置解池參數，允許輸出多個滿足時長約束的分配方案。

Step8：執行算法。每確定一個機組的容器分配順序和數量，各機組外運緊迫性也會隨之進行更新迭代，直至將空容器全部分配完畢。

Step9：輸出結果。輸出單次運輸計劃總運輸時間、貨包視角的裝/卸料開始及結束時間、各機組分配的容器數以及多個具體可行方案。

3 算例驗證

3.1 算例信息

以2個電站、12臺機組為例，設定10臺容器、3個作業面和2個后處理廠，裝料開始時間為2022年11月11日。各機組池中組件狀態信息見表2，各機組與后處理廠的不可裝卸料時間窗信息分別見表3和表4，各機組的外運緊迫性見表5。

表2 池中組件狀態信息Table 2 Spent fuel assembly status

表3 機組不可裝料時間窗Table 3 Unit unavailable charge date

表5 機組外運緊迫性Table 5 Unit transport urgency

首先根據池中組件狀態信息，結合乏燃料最小冷卻時間表，確定每個機組最多可外運的組件數，以確定各機組可分配的容器上限。

其次根據各機組的外運緊迫性和不可外運時間窗，將既有的容器分配給各機組，得到若干個可行且在時間上最優的方案。

最后根據運輸各子環節預設時間，推導每個容器開始裝料與裝料完成時間，開始卸料與卸料完成時間，并分析得到的方案是否符合從裝料開始到卸料結束的時間約束。

算法結果最終輸出多個滿足約束條件的可行方案。以第一個輸出方案為例，求解結果如表6所示，A電站內A1機組分配3個容器，A5機組分配2個容器，D電站內D1機組分配3個容器，D4機組分配2個容器，單次運輸計劃總運輸時長為137天，各容器運輸時間均滿足180天約束。此外，算法將輸出具體可行方案運輸批次及時間節點，如表7所示，第一批次裝料計劃分配給A1、A3、D1各1臺容器，第二批次分配給A3、D1、D4各1臺容器，第三批次分配給A1、D1、D4各1臺容器，第四批次分配給A1機組1臺容器。

表6 第1種方案求解結果Table 6 Plan 1 solution result

表7 第1種方案的時間約束判定Table 7 Plan 1 time constraint determination

3.2 仿真結果

在乏燃料實際單次運輸計劃中存在許多不確定性，造成優化方法應用到實際運輸過程上的局限性。離散仿真系統具有很好的模擬實際運輸過程不確定情況的能力，但不具備良好的優化能力。通過仿真軟件中搭建乏燃料單次運輸計劃模型與算法的結果相結合的方式，驗證裝料排期方案的合理性。建立仿真模型以模擬乏燃料單次運輸計劃的運輸過程，將算法所需數據輸入所建混合整數規劃模型中，運用啟發式算法求解出裝料排期方案，將優化方案輸入仿真模型中推演，與人工排期方案的仿真推演結果作對比，驗證算法輸出方案的可執行性與優化性。

由表8可知，人工排期方案中A3機組分配容器數過多，而算法優化計劃的容器分配更為均勻，理論上機組不會出現或較少出現裝料排隊現象。

表8 裝料計劃容器分配數量對比Table 8 Charge container allocation comparison

通過仿真系統分別輸入人工排期計劃、算法優化計劃的數據進行流程模擬，對比乏燃料單次運輸計劃各環節所需時長及各容器的時間信息，見表9。

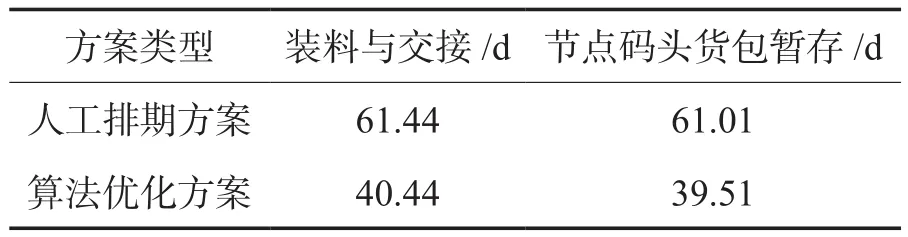
表9 各環節所需時間對比Table 9 link time consumption comparison

從表9可知，算法優化方案中的“裝料與交接模塊”時長約40 d，較人工排期方案中的“裝料與交接模塊”時長約61 d節約21 d，同時受裝料時間影響，算法優化方案較人工排期方案的“節點碼頭貨包暫存模塊”時長節約22 d左右。

由表10可知，人工排期方案和算法優化方案均能滿足時間約束，但算法優化計劃中各貨包占用的時長短于初始裝料計劃，使得單次運輸計劃更具可執行性。

表10 貨包時間信息對比Table 10 Package existence time comparison

綜合上述容器分配數量、各環節所需時間和貨包時間3個方面的對比，表明提出的模型在運輸計劃裝料排期環節的優化方案，有效縮短了整個裝料環節時間，提高了運輸計劃的可執行性。

4 結束語

本文針對乏燃料單次運輸計劃中多約束的裝料排期問題，以最小化運輸時間為目標建立了優化模型，利用基于優先規則的啟發式算法求解該混合整數規劃模型。在算例分析中，分析多約束條件對裝料排期的影響，結果表明該優化方案推演的運輸時長優于人工排期方案，不僅節省大量人力，還為乏燃料單次運輸計劃的制訂提供實用價值。