閥門流量系數的測量原理與方法研究

宋延勇，蘇明旭，王子安

(1.上海儀器儀表自控系統檢驗測試所有限公司，上海 200233；2.上海理工大學能源與動力工程學院，上海 200093)

0 引言

閥門是一個可變節流件，是流體控制系統的重要組成部分，在能源、化工、水利等領域的應用極其廣泛[1]。由于應用對象的多樣性和復雜性，閥門的類型非常多。閥門根據結構可分為直通單座閥、雙座閥、閘閥、蝶閥等；根據用途可分為低溫閥、高溫閥、超高壓閥、小流量閥等。除閥門口徑、耐壓強度等較為容易測量的參數外，反映閥門流通能力大小的流量系數是較難測量的關鍵閥門參數。

目前，閥門的種類繁多，給閥門流量系數的規范測量帶來了比較大的挑戰[2]。特別是涉及閥門雷諾數的計算和流體流動狀態的判定，不同標準給出了差異較大的計算式和參考值。對閥門流量系數測試與應用中的雷諾數限值也有不同的參考值[3-5]。典型的無需修正雷諾數最小限值有3 500、10 000、40 000等，差異較大。

本文從流體力學基本原理出發，研究閥門流量系數的測量原理，比較了閥門與圓形截面管道在雷諾數計算方法和流動狀態判定的差異，探討了閥門雷諾數修正系數與雷諾數的關系，分析了閥門流量系數測量中的壓差和雷諾數的要求。上述工作能夠為從事閥門開發與應用的工程人員提供有價值的線索。

1 閥門流量系數測量原理

閥門流量系數表征控制閥流通能力的大小，采用在規定條件下單位時間內流過閥門的流體的體積數值與壓差的函數關系表示。閥門流量系數C根據單位制的不同分別用Kv和Cv表示。國內一般使用Kv，而國外采用英制單位，通常用Cv。1Kv=0.865Cv[6]。Kv在數值上相當于在壓差為100 kPa時，每小時流過閥門的水的立方米體積數值。

閥門流量系數測量原理如圖1所示。

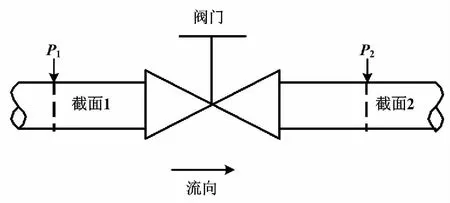
圖1 閥門流量系數測量原理示意圖

假設流體為不可壓縮黏性流體，由于流體黏性的影響，維持黏性流體的流動需要消耗機械能，所以理想流體伯努利方程反映的流動中總機械能守恒的規律不再成立。當流體流經閥門阻力件時，在閥門前后非急變流的截面1和截面2處建立不可壓縮黏性流體總流的伯努利方程[7]。

(1)

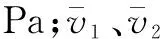
(2)

式中：hj為單位重量流體的局部阻力損失，J/N;ζ為局部阻力系數，是1個無量綱系數。

將式(2)代入式(1)，得：

(3)

式中：Δp為閥門前后壓差，Δp=p1-p2，Pa。

流經閥門的體積流量為：

Qv=vA

(4)

式中：Qv為流經閥門的體積流量，m3/s；A為閥門公稱截面積，m2。

將式(3)代入式(4)，得：

(5)

(6)

根據量綱齊次原理，量綱[C′]= [L2]。當采用國際單位制基本單位時，C′的單位為m2。由于C′有量綱，根據使用單位制，其數值會有不同。

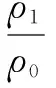
(7)

系數N1用于不同單位制之間的換算。換算系數如表1所示。表1給出了采用國際單位制基本單位、法定單位和英制單位對應的Kv和Cv的系數值。

表1 換算系數表

例如，當選擇流量單位為m3/h，壓差單位為kPa，相對密度為1時(介質為5～40 ℃的水)，將換算系數表代入式(7)，可得：

(8)

式(8)與GB/T 4213—2008標準中的氣動調節閥流量系數計算式一致。

將式(6)代入式(7)，則當采用國際單位制基本單位且相對密度為1時，可得：

(9)

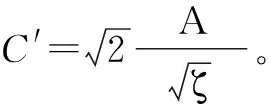
將C′代入式(9)，可得Kv與阻力系數ζ的關系為：

(10)

由式(10)可知，Kv值與閥門阻力系數的平方根成反比，與閥門截面積成正比。相同口徑閥門的Kv值越大，則阻力系數越小；相同阻力系數閥門口徑越大，則Kv值越大。上述方程以不可壓縮黏性流體的伯努利方程式為基礎，適用于非阻塞流工況及不可壓縮粘性流體。

2 流動狀態判定與閥門雷諾數

黏性流體流動具有層流和湍流(紊流)這2種不同的流動狀態。流動狀態不僅與流體流速、流體的運動粘度有關，還與通道的特征尺寸有關。圓管內流動特征尺寸為管內徑D，不同的流體粘度、密度、管內徑都會導致不同的臨界雷諾數，用于區分層流和紊流。

流態可以用無量綱準則數雷諾數大小進行判定。

(11)

式中：Re為雷諾數值；v為管道流速， m/s；D為管道內徑，m；ν為流體運動粘度，m2/s。

對于圓管內流動，無論流體的物性與管徑如何變化，工程上通常取圓管的臨界雷諾數Re,c=2 000。即Re≤2 000時，管內流動為層流；反之，則為湍流。

由于閥門結構形式差異較大，流道設計多樣，所以相對于圓管內的流動，閥門內的流體流動更為復雜，尚無統一的臨界雷諾數值。而閥門雷諾數的計算式也存在不同的表示方式，因此流動狀態判定更加困難。

區別于圓管內雷諾數Re，下文用Re,v表示閥門雷諾數。

對單一流路的調節閥，如直通單座閥、套筒閥或球閥，當流量單位為m3/h時，閥門雷諾數的計算式為：

(12)

對于具有2個平行流路的調節閥，如直通雙座閥、蝶閥或偏心旋轉閥等，閥門雷諾數計算式為：

(13)

與式(12)和式(13)相比，式(14)中加入閥門的類型修正和液體壓力恢復系數修正，統一了閥門雷諾數計算式，并給出了部分類型閥門的修正值。

(14)

更全面、復雜的閥門雷諾數計算如式(15)所示。

(15)

式中：Fd和FL分別為被測閥門的類型修正系數和液體壓力恢復系數，均為無量綱數。

在閥門測試中，以試驗管道內徑作為特征尺寸計算雷諾數[8]和采用閥門雷諾數會有計算差異。不同方法雷諾數計算結果的差異如表2所示。

表2 不同方法雷諾數計算結果的差異

表2中：序號1和序號2是流量系數較小的閥門在5%開度和全開條件下的試驗數據；序號3是流量系數較大的閥門在全開條件下的試驗數據。當閥門的開度較小時，式(11)的計算結果差異較大。當閥門全開時，各式計算結果差異相對較小。

閥門雷諾數具有非常重要的作用，具體體現在以下2個方面。一方面，閥門雷諾數可用于判定閥門內的流體狀態，在閥門流量系數的測量中，需要確定測量條件處于充分紊流狀態。另一方面，當閥門應用于低雷諾數場合，可根據閥門雷諾數確定雷諾數系數，從而準確驗算閥門流通能力，確保閥門正確選型。

3 閥門雷諾數系數與界限雷諾數

閥門流量系數與阻力系數的平方根成反比。阻力系數與閥門的結構形狀有關。不同結構的閥門阻力系數差異較大，如球閥、蝶閥等流阻小，單座閥、高壓閥等流阻大。對于同口徑的閥門，前者具有大的Kv值，流通能力強。阻力系數還和流態有關。參考沿程阻力系數雷諾數的變化規律，可知閥門阻力系數隨雷諾數的變化規律在層流區、臨界區和紊流區是各不相同的。除個別情況以外，難以從理論上推導局部阻力系數的計算式。因此，往往由試驗測出不同雷諾數的閥門阻力系數。通常情況下，阻力系數將隨著雷諾數的增加而逐漸保持穩定。阻力系數保持穩定所需的最小雷諾數被稱為界限雷諾數。

由閥門流量系數Kv值與阻力系數的關系可知，Kv值同樣遵循上述規律，即Kv值是雷諾數的函數。在工程應用中Kv值特指在紊流條件下閥門處于全開或特定開度下的流通能力，實際上通常是在界限雷諾數之上未形成阻塞流時的流量系數，即流量系數保持穩定時的Kv值。

當液體粘度高或流速小，以致通過調節閥的流體為低雷諾數的非紊流狀態或低于界限雷諾數時，計算K′v值與界限雷諾數之上的常數Kv存在差異。因此，在低雷諾數進行Kv值的測量和流量的計算需要進行雷諾數修正。

通常采用雷諾數系數FR修正低于界限雷諾數條件下測得的閥門流量系數K′v值或進行流量驗算。雷諾數系數是通過在特定雷諾數下測得的流量系數與高于界限雷諾數條件下測得的流量系數的比值。雷諾數系數也是雷諾數的函數。

(16)

式中：FR為閥門雷諾數系數；K′v為低雷諾數下的閥門流量系數。

根據安裝條件下流體流量的計算式[9]，可得雷諾數系數的擬合計算式，見式(17)和式(18)。需要注意的是，擬合式所用閥門雷諾數應由式(15)計算。對擬合式未包括的特殊類型閥門或為獲得更準確的雷諾數修正系數，可采用試驗法測出隨雷諾數變化的流量系數值，獲得特定的雷諾數系數曲線或擬合式。

當Re,v<10時：

(17)

當Re,v≥10時：

(18)

式中：n為常量，其值取決于閥內件類型。

對于全尺寸閥內件，n的取值見式(19)。

(19)

應用雷諾數系數的擬合計算式得到DN50口徑。流量系數Kv值相同的不同類型閥門的雷諾數修正系數如圖2所示。

圖2 不同類型閥門的雷諾數修正系數

不同類型的閥門在低雷諾數范圍內的修正系數是不同的，應采用不同類型閥門的系數修正，以提高低雷諾數范圍的流量系數的計算準確度。當雷諾數大于10 000時，雷諾數系數保持恒定。這說明以式(15)計算閥門雷諾數作為判定依據時，可以認為閥門雷諾等于10 000是流量系數保持穩定的界限雷諾數。

4 閥門流量系數測量中的壓差和雷諾數要求

以下是2種常用的閥門流量系數的試驗方法。這2種方法對閥門流量系數測試的安裝與測量儀表的要求基本一致，但對測試過程的壓差和雷諾數等參數要求存在較大差異。

方法1要求閥門應在紊流、無空化區域內3個間隔較大的壓差點上進行測量，但不低于10 kPa；每次流量試驗得到的3個值中，最大值不應大于最小值的4%；結果取3個測量值的平均值。建議壓差1為恰好在空化點以下或試驗裝置可獲得的最大值，壓差2取壓差1的50%，壓差3取壓差1的10%。對流通能力很小的閥門要求取較大的壓差，當大口徑控制閥試驗裝置達到極限時，可以使用較小的壓差，但不低于10 kPa。上述均須確保為紊流，推薦閥門最小雷諾數為1×105。對不同的壓力恢復系數FL和壓差值，為確保液體充滿試驗段下游部分，并防止液體氣化，規定了最低入口絕對試驗壓力。

方法2要求閥門在大于或等于35 kPa的3個壓差下(增量不小于15 kPa)測量并分別求得流量系數；每次流量試驗得到的3個值中最大值不應大于最小值的4%；結果取3個測量值的平均值。當閥門的額定流量系數很小或很大時，只要能保持紊流，即在保證閥門雷諾數大于4×104的前提下，可以選用其他合適的壓差值。

采用2種方法在相同安裝條件下測試同一閥門的額定流量系數，被測閥門口徑為DN50，試驗介質為水。2種方法的測試結果偏差如表3所示。

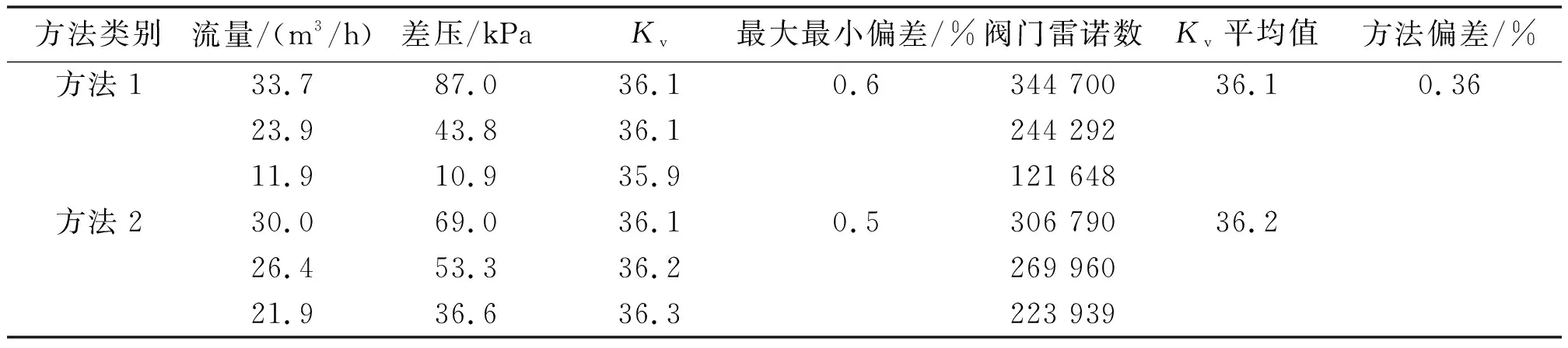
表3 2種方法的測試結果偏差

由表3可知，2種方法的測試結果偏差為0.36%，優于±5%的試驗精確度要求。2種方法主要對測量過程中的雷諾數和測量點壓差提出了要求，對一般閥門均適用且測量結果具有較好的一致性。但是對于流通能力特別大或特別小的閥門，以及流量系數和阻力系數處于極端范圍的閥門，兩者都放寬了雷諾數或壓差要求，但還是難以滿足實際測試需求。

極端范圍下的流量系數測試結果如表4所示。

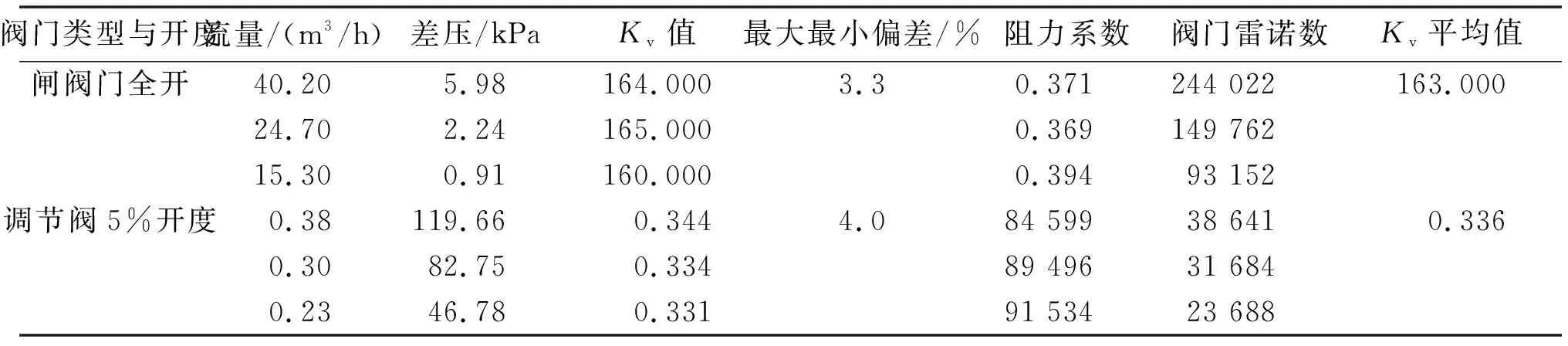
表4 極端范圍下的流量系數測試結果

表4中，試驗對象分別為DN50口徑全開狀態閘閥和相同口徑10%開度狀態調節閥，試驗介質為水。閘閥在全開條件下流量系數比較大，阻力系數非常小導致壓差非常低，在試驗裝置的流量極限能力下難以達到方法1的不低于10 kPa的要求，但是雷諾數已大于界限雷諾數。調節閥在5%開度條件下流量系數比較小，阻力系數非常大導致壓差非常大。在試驗裝置的流量極限能力下，雷諾數仍不滿足方法2的最低要求，但是已大于界限雷諾數的要求。要達到更高的雷諾數，就要在不產生阻塞流的情況下增加入口壓力。這將帶來更高的檢測成本，但對檢測結果的精度提高不明顯。

因此，對于流量系數和阻力系數處于相對極端范圍的閥門，在進行流量系數的測量時首先應確保測試流量點的閥門雷諾數大于界限雷諾數，其次應盡量采用測試裝置的能力上限并確保未形成阻塞流，而對差壓的要求可放寬。在實際測試過程中可遵循以上原則，并在充分考慮測量誤差最優的基礎上采用合適的差壓值，在不同的閥門雷諾數下進行流量系數測量以及取平均值。

5 結論

本文基于流體力學的基本原理，研究了閥門流量系數的測量原理與方法、閥門雷諾數計算方法、閥門流量系數與雷諾數關系，以及雷諾數修正系數，并分析了流量系數測量中的差壓和雷諾數要求，得到以下結論。

閥門雷諾數用于低雷諾數場合的雷諾數系數計算或判定閥內流動狀態時，應選用適當的閥門雷諾數計算式。

閥門雷諾數系數不僅與閥門雷諾數有關，還與閥門的結構和類型有關。為得到更準確的數據，可采用包含類型的擬合式，或對特定閥門進行實流檢測。

通過閥門雷諾數系數與閥門雷諾數變化曲線，本文提出了典型的閥門界限雷諾數值。當閥門雷諾數大于界限雷諾數時，閥門流量系數基本保持不變，在此狀態下測得的流量系數即為閥門流量系數。

目前標準給出的不同閥門流量系數測量方法，對一般閥門的測試結果具有較好的一致性。但是對于流通能力相對特別大或特別小的閥門，應確保測試流量點的閥門雷諾數大于界限雷諾數，盡量使用測試裝置的能力上限并確保未形成阻塞流，對差壓的要求可進一步放寬。

由于閥門結構和種類的多樣性，導致特殊應用時相關的計算式較復雜，目前已有的擬合式也僅適用于特定的閥門類型。對于特殊的閥門，可遵循類似的原理，通過試驗和分析獲得更準確的閥門雷諾數系數。