切出風速下風力機變槳故障葉片氣動特性及準靜態結構響應分析

劉一鳴，李 春，王淵博，李 根，閆陽天

（上海理工大學 能源與動力工程學院/上海市動力工程多相流與傳熱重點實驗室，上海 200093）

化石燃料的過度使用及能源結構的不合理導致溫室效應和環境污染等問題，且在不久的將來還可能導致資源枯竭之境況。為此，國家“十四五”規劃綱要對發展風電等清潔能源提出了明確要求。不僅我國，世界各國均遭遇同樣問題并都積極開發風能資源。此外，現代風力機通常均安裝葉片變槳系統，然而變槳系統為風力機所有部件中故障率最高，且一旦發生故障將導致風力機無法正常運行時間最長的關鍵子系統之一，但鮮見與此相關氣動及結構方面的研究。因此，在同時兼顧流體域和固體域基礎上，對風力機特定狀態下變槳故障葉片進行數值計算以探究其氣動特性及結構響應顯得尤為重要。

對于風力機變槳故障，國內外學者進行了一些研究。Ronsten通過實測相關數據提出風力機停機后葉片狀態將影響其力矩大小及壓力分布。據此不難推斷，停機后變槳故障與變槳成功葉片由于狀態差別極大，受載亦將存在較大差異。Tian等基于數值模擬方法并采用獨立變槳技術控制大型三葉片水平軸風機運行，結果證明該策略可有效減小葉片載荷變化范圍及風輪轉矩波動幅度。因此，該獨立變槳技術能保證葉片時刻處于最佳攻角，旋轉過程中葉片狀態始終較為穩定，而風力機發生變槳故障時則與此情況相反。Chen等通過研究臺風“天兔”襲擊汕尾紅海灣風電場事件，指出變槳系統故障與風力機大面積嚴重損毀情況存在很大聯系。閆學勤等采取將葉片方位角權系數分配與葉根氣動載荷反饋相結合的變槳新技術進行葉根揮舞力矩及輪轂傾覆力矩控制，結果顯示新型獨立變槳技術可保證葉片具有低變槳故障率和小變槳誤差。任年鑫等研究了臺風達到兆瓦級水平軸風力機切出風速時，風力機順槳停機后變槳故障與變槳成功葉片的受載情況，結果證明，風力機葉輪方位角及臺風切入方向會對葉片受力產生影響，且變槳故障葉片載荷總大于變槳成功葉片。

由上述研究可知，風力機變槳故障對葉片受載影響極大，故此時葉片結構亦最危險。然而，在絕大多數研究中僅考慮了氣動側載荷卻未涉及結構側響應。此外，切出風速下變槳故障葉片受載及入流風速極大，但該風況下的風力機變槳故障研究鮮見相關報道。因此，本文針對NREL 5 MW風力機在切出風速下變槳故障葉片展開研究，對比分析變槳成功及各典型方位角下變槳故障葉片氣動特性，然后開展變槳故障葉片準靜態結構響應分析，以期為葉片結構設計提供更全面的參考數據。

1 研究對象及數值計算模型

1.1 葉片參數化建模及鋪層

葉片是風力機最為關鍵的部件。本文利用Unigraphics NX軟件建立NREL 5 MW風力機葉片三維實體模型，如圖1所示，其中對關鍵部位進行了放大顯示。

圖1 NREL 5 MW風力機葉片模型Fig. 1 Blade model of NREL 5 MW wind turbine

由于本文結構側計算涉及有限元分析，因此在Unigraphics NX軟件中完成NREL 5 MW風力機三維實體建模后，還需對其賦予相關材料屬性。共選取9種單一材料，通過對材料種類、纖維方向以及鋪層順序進行組合便可得到適用于風力機葉片各部位的復合材料。例如，葉片主梁帽需要承擔彎曲載荷，可以選擇抗拉性強的碳纖維和玻璃纖維并使纖維方向順著葉片展向進行鋪層，便可滿足梁帽的結構力學性能要求，其他部位鋪層方法類似。最終葉片鋪層方案如圖2所示。通過Abaqus軟件Property模塊的Composite Layup功能進行NREL 5 MW風力機葉片復合材料鋪層。這與真實風力機葉片結構設計和制造工藝相同，從而可保證計算結果能夠直接為相關設計制造及實際工程問題提供參考。

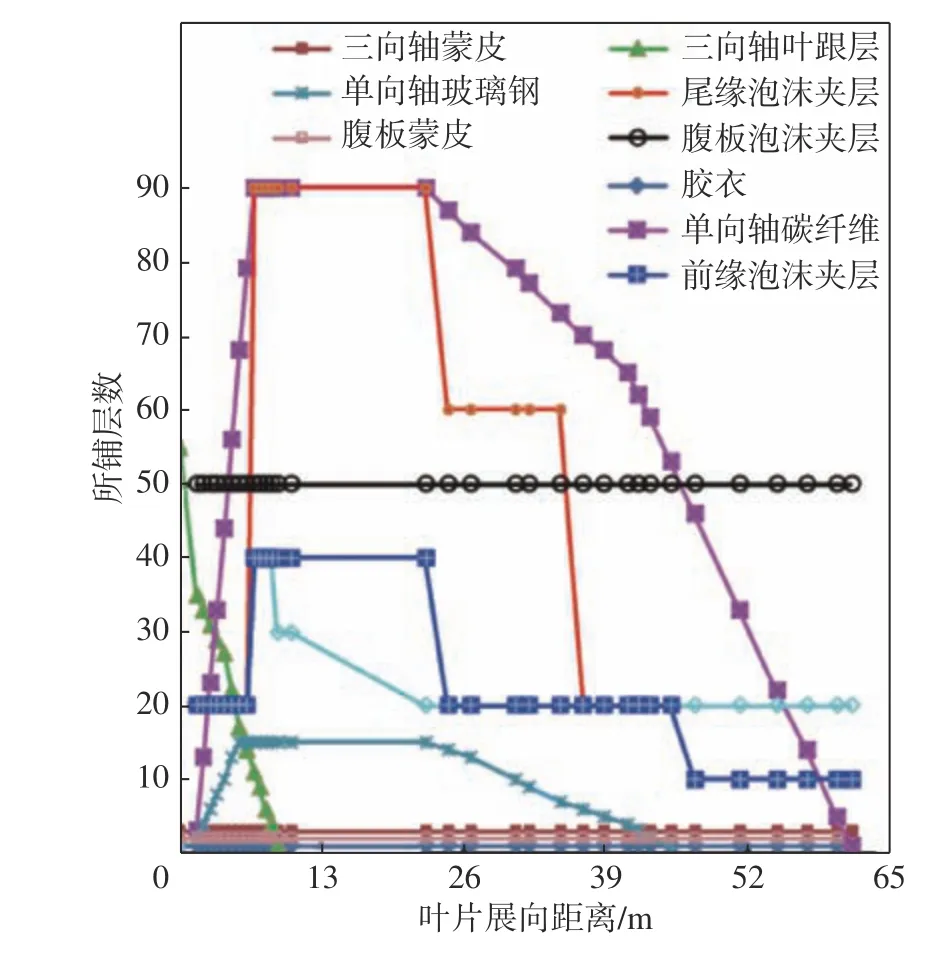
圖2 葉片鋪層方案Fig. 2 Blade layout

1.2 氣動側模型

氣動載荷分析需通過與葉片同步旋轉的局部坐標系定義各方向力矩。葉片坐標系及各方向力矩如圖3所示。

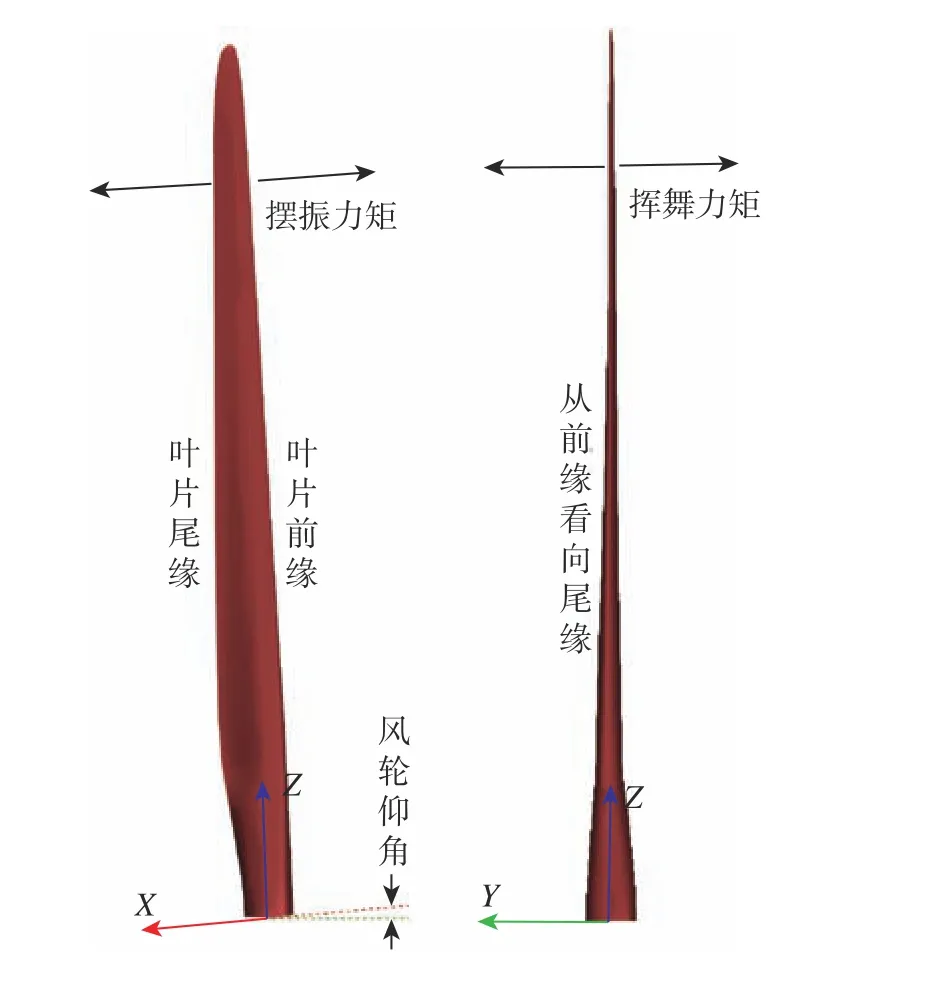
圖3 葉片坐標系及各方向力矩Fig. 3 Blade coordinate system and torque in all directions

為降低計算域邊界對數值模擬的影響并減小風洞阻塞效應，需盡可能擴大計算域尺寸以增加風力機葉片與各邊界間的距離。本文中計算域以及邊界條件如圖4所示，圖中右下角坐標系為數值模擬全局坐標系，為風輪直徑126 m。入口邊界條件為指數率風剪切速度入口，參高度處是NREL 5 MW風力機25 m·s的切出風速，地面粗糙度指數選為0.16，出口為壓力出口，其值為1個準大氣壓.地面為無滑移壁面，頂面是對稱平面。兩側面采用周期性邊界條件，即計算域一側面網格節點與另一側面網格節點一一對應，某側周期邊界計算域外“鏡像單元”信息由緊鄰另一側周期邊界計算域內的單元提供。CCM+前處理創建高質量多面體網格，且壁面邊界層采用低處理（＜1）。近壁面網格高度為5×10m，邊界層網格共24層，總厚度為0.1 m。同時為使風力機數值模擬準確度更高，對其尾跡

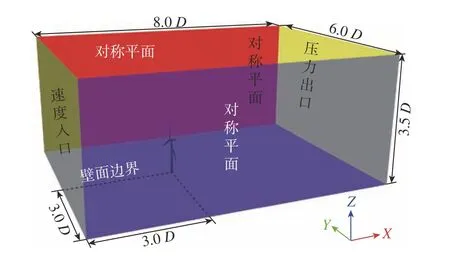
圖4 計算域以及邊界條件Fig. 4 Calculation domain and boundary conditions

計算域最終網格分布如圖5所示。由圖中可看出，相較于采用四面體網格，全部采用多面體網格類型能以更少的網格數量達到相同的計算精度。本文中氣動側均利用計算流體力學軟件STAR-區域作了加密處理。

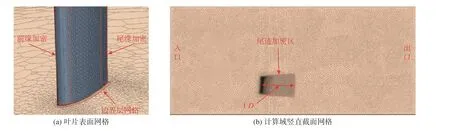
圖5 網格分布Fig. 5 Grid distribution

數值計算采用隱式非定常算法（implicit unsteady），時間步長為0.001 s，對流項與時間項的離散均使用二階格式，壓力-速度解耦基于SIMPLE算法，湍流處理采用SST模型，湍流強度取0.05，湍流長度尺度為1.0 m。當數值模擬運行至載荷處于相對穩定或呈周期性振蕩時，則判定為已收斂。

1.3 結構側模型

圖6為流固耦合結構側計算模型。風力機葉片幾何模型由片體（無厚度曲面）構建，這是由于有限元分析中若三維結構某一方向尺寸遠小于另外兩個方向尺寸即可采用片體模型，如此既能保證精度又可節省相當多的計算資源。同樣為節省計算資源，將風力機葉片劃分為結構化網格。與非結構化網格相比，結構化網格生成速度快且質量高，基于結構化網格數值計算的數據存儲結構更簡單且占用計算內存較少。有限元分析中片體結構化網格適合使用S4R單元，其為一種通用殼單元類型，既可應用于厚殼問題求解，亦能應用于薄殼模型計算。此外，將葉根一圈通過運動耦合約束在葉根圓形的中心點（即約束點）上，然后在該約束點施加ENCASTRE邊界條件對六個自由度同時進行約束。

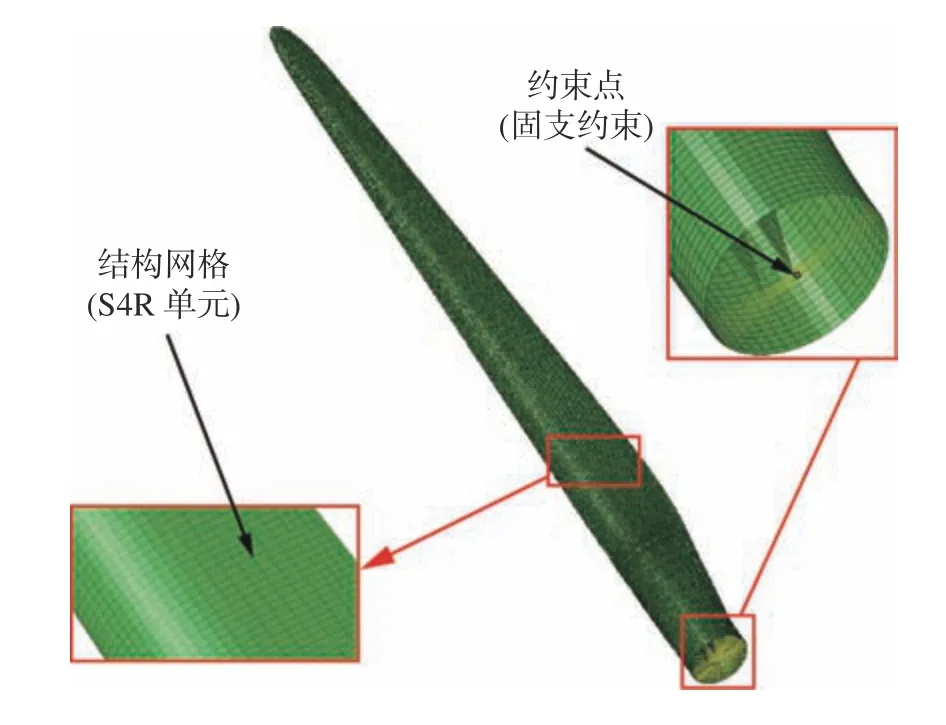
圖6 結構側計算模型Fig. 6 Calculation model for blade structure

2 準靜態結構分析方法

2.1 雙向弱流固耦合

雙向弱流固耦合流程如圖7所示。該流程共有8個步驟，對各步驟的解釋分別為：①對固體域進行網格劃分及物理模型設置，并參考氣動計算結果施加一個近似載荷條件，然后單獨運行一段時間以驗證結構側相關設置的準確性及可行性；②流體域保留氣動計算數據結果，并對多面體網格應用Morphing功能以控制其變形；③判斷流固兩側柔性結構是否完全匹配，若一切正常便可通過Import mode程序導出流體域柔性結構所受壓力和黏性剪力，并通過abaqus關鍵字加載至固體域柔性結構上；④對結構側進行計算，柔性結構變形等數據保存至ODB文件；⑤首先將結構側的ODB文件加載至Import mode程序，其次由Import mode程序提取其中變形數據傳遞給STAR-CCM + ，最后STAR-CCM +對柔性結構形狀進行更新，同時利用Morphing功能控制計算域網格變形以適應當前柔性結構形狀；⑥對流體域進行計算并得到柔性結構新的壓力以及黏性剪力；⑦重復前面第③～⑥步直至流固兩側相關特征不再有明顯變化為止（本文中流固兩側數據共交換4次）；⑧雙向弱流固耦合數值模擬完成。

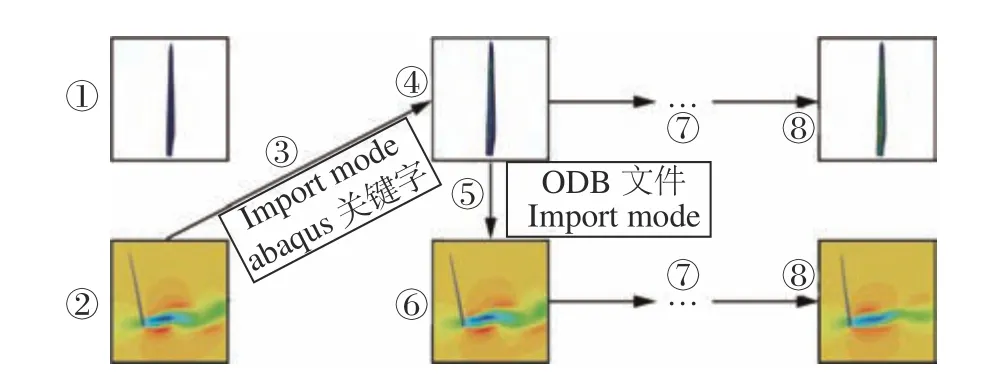
圖7 雙向弱流固耦合流程Fig. 7 Flow chart of two-way weak fluid-structure coupling

2.2 屈曲分析

細長結構體由于長度方向尺寸遠大于另外兩個方向尺寸而表現出柔性特征，當受到微小載荷或擾動后便易發生失穩。當這些外部微小影響消失后，細長彈性體能夠恢復至穩態，但若載荷或擾動較大時，細長彈性體則很可能發生屈曲。目前風力機大型化趨勢非常明顯，風力機越來越長導致其柔性增加，NREL 5 MW風力機葉片長達61.5 m，屬于標準的細長彈性體，因此有必要對其進行屈曲分析。屈曲分析一般分為線性與非線性，基于線性屈曲所研究的結構并不會發生塑性變形，而是在結構彈性階段產生彈性失穩。線性屈曲分析最終所得臨界載荷可能會稍大于結構發生屈曲時的實際值，但線性屈曲分析計算效率非常高，且可作為結構分析時的前期預估值，故本文采用線性屈曲分析。

3 結果分析

3.1 單葉片模型可行性驗證

首先對比全葉輪模型（full rotor model，FRM）與單葉片模型（single blade model，SBM）的計算結果，以便為減少計算量的策略提供理論依據。圖8為SBM與FRM揮舞力矩和擺振力矩時域圖。對比圖8（a）、（b）中的力矩可知：SBM與FRM揮舞力矩和擺振力矩時域曲線基本重合，初步證明了基于SBM計算的可行性。

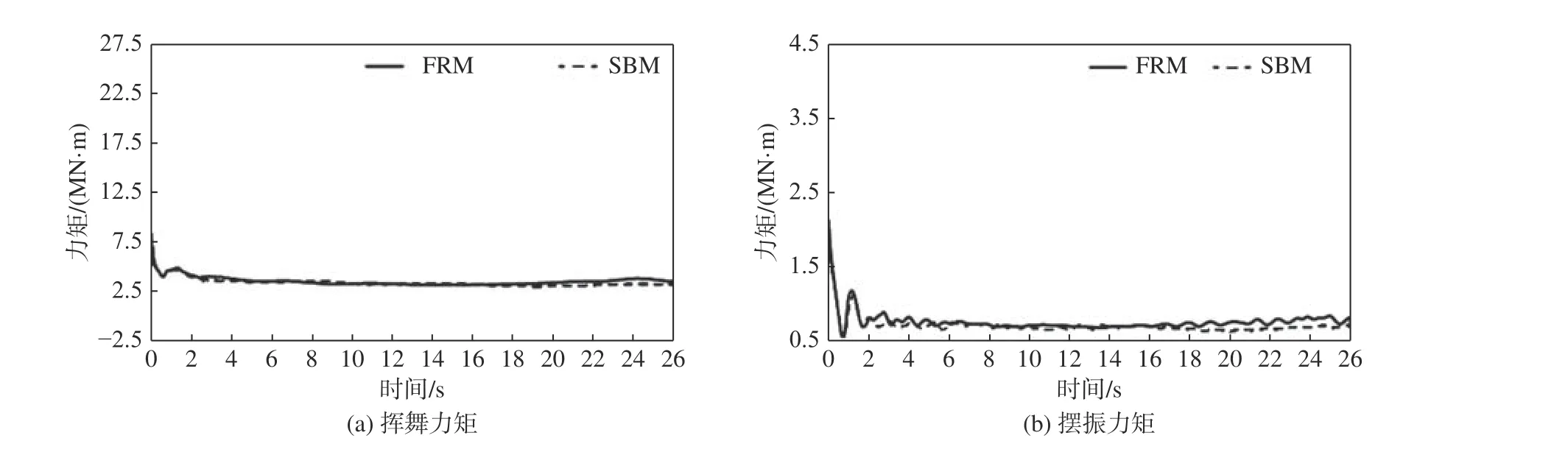
圖8 SBM與FRM揮舞力矩和擺振力矩時域圖Fig. 8 Time domain spectra of flapwise moment and edgewise moment for SBM and FRM

將SBM和FRM揮舞力矩和擺振力矩脈動時域序列進行快速傅里葉變換，可得到表1中的SBM與FRM載荷脈動主要刺激頻率。由表中可以看出，SBM與FRM揮舞力矩和擺振力矩主要刺激頻率相同或極其接近，這更進一步證明了水平軸風力機SBM與FRM載荷脈動差異非常小。

表1 SBM與FRM載荷脈動主要刺激頻率Tab. 1 Main excitation frequency of load pulsation for SBM and FRM (單位：Hz)

經過葉片頂點且與葉片坐標系軸垂直平面上SBM與FRM在軸方向的葉尖渦量場如圖9所示。從圖中可觀察到，SBM與FRM葉尖渦大小及位置幾乎完全相同，說明SBM與FRM流場流動狀況極為接近，此亦為SBM與FRM載荷頻域主要刺激頻率以及力矩時域曲線差別甚微的根本原因。綜上可知，使用SBM進行數值模擬具有較高的準確性及可行性，故后文均基于SBM開展計算。

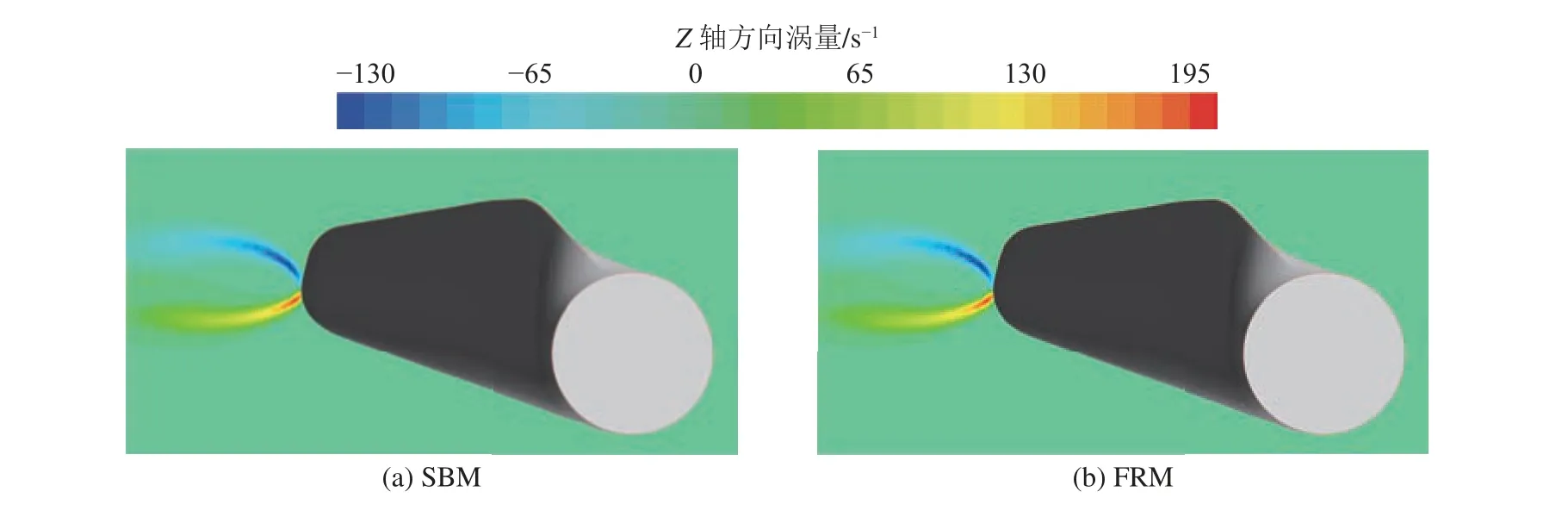
圖9 SBM與FRM在Z軸方向的葉尖渦量場Fig. 9 Blade tip vortex of SBM and FRM in Z-axis direction

3.2 變槳故障葉片氣動特性

圖10為NREL 5 MW風力機在切出風速下變槳故障與變槳成功葉片揮舞力矩和擺振力矩。對比圖10（a）、（b）可看出，揮舞力矩比擺振力矩大1個數量級，但都表現出變槳故障葉片力矩大于變槳成功葉片的特征，其中變槳故障葉片揮舞力矩平均值為變槳成功葉片的13.8倍。

為進一步分析變槳故障葉片與變槳成功葉片的差異，對周圍流場速度云圖進行分析，結果如圖11所示。由圖中可知，變槳故障葉片的尾跡較變槳成功葉片的更為明顯。這是因為變槳故障葉片從來流風中吸收了更多能量，因此變槳故障葉片的受載比變槳成功葉片的大，這一結果與圖10中的數據非常吻合。綜上，后文僅分析變槳故障葉片特征。

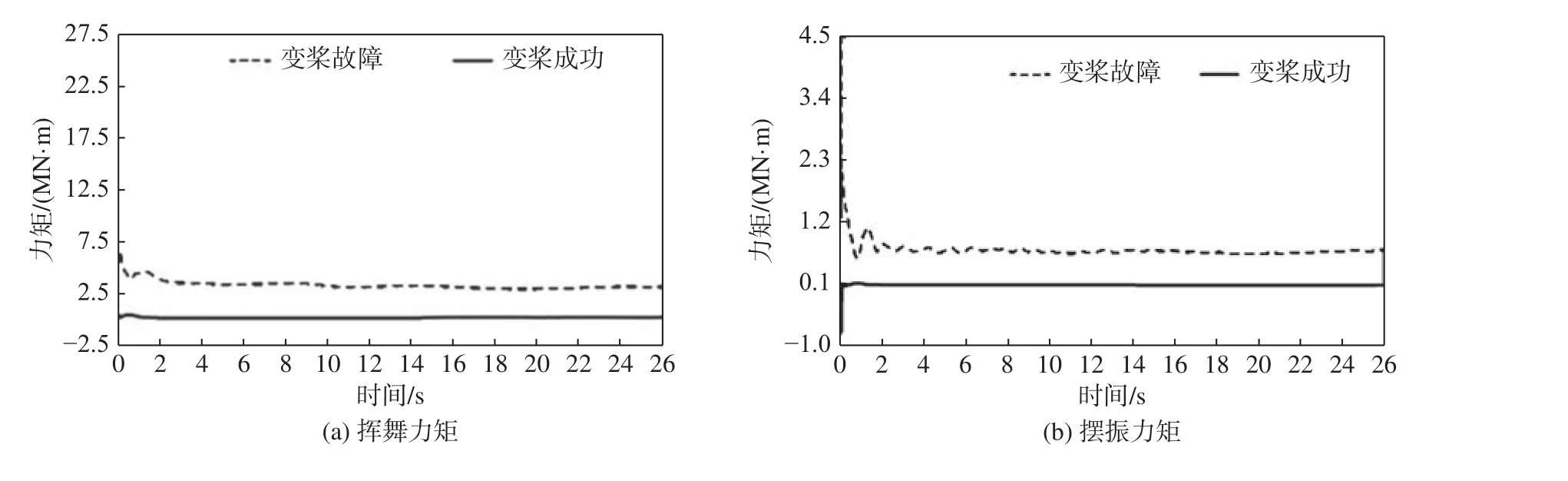
圖10 變槳故障與變槳成功葉片揮舞力矩和擺振力矩Fig. 10 Flapwise moment and edgewise moment of a blade under fault and normal status of pitch system

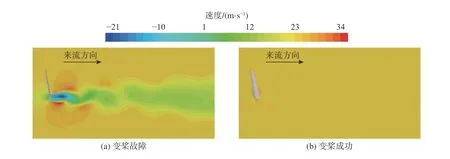
圖11 變槳故障葉片與變槳成功葉片周圍流場速度云圖Fig. 11 Velocity contour around a blade under fault and normal status of pitch system

NREL 5 MW風力機達到切出風速停機后葉輪方位角是隨機的。圖12為0°、60°、120°、180°、240°和300°共6個方位角下變槳故障葉片揮舞力矩和擺振力矩時域圖。從圖12（a）中可看出，0°方位角下揮舞力矩最大，其次是60°和300°方位角下的，然后是120°、240°、180°方位角下揮舞力矩最小。揮舞力矩在各方位角下的差異主要是由風剪切造成風速從地面沿豎直方向越來越大所致，故0°方位角葉片平均來流風速最大，180°方位角葉片平均來流風速最小。此外，60°與300°方位角以及120°與240°方位角葉片平均來流風速兩兩相同，因此它們的力矩大小也一樣，故后續研究僅分析60°和120°方位角，對300°和240°方位角的結果不再贅述。

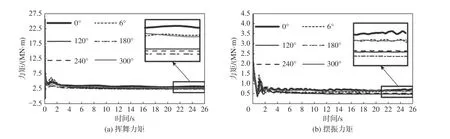
圖12 各方位角下變槳故障葉片揮舞力矩及擺振力矩時域圖Fig. 12 Time domain spectra of flapwise moment and edgewise moment of a blade with pitch fault at different azimuths

3.3 準靜態結構響應分析

圖13為雙向弱流固耦合葉片應力及葉尖位移。由圖中可知，切出風速下4個典型方位角的變槳故障葉片均出現了應力集中現象，其中0°方位角下變槳故障葉片應力集中最強，為9.886 MPa，而180°方位角下應力集中最弱，為6.932 MPa，后者較前者降低了29.8%。葉尖位移變化趨勢與應力集中變化趨勢相同，從0°、60°、120°到180°方位角下葉尖位移逐漸減小，其中180°方位角下變槳故障葉片葉尖位移較0°方位角下的減少了32.7%。此外，還發現雙向弱流固耦合結構側結果與圖12中氣動力矩情況吻合較好，證明了本文計算結果的準確性。

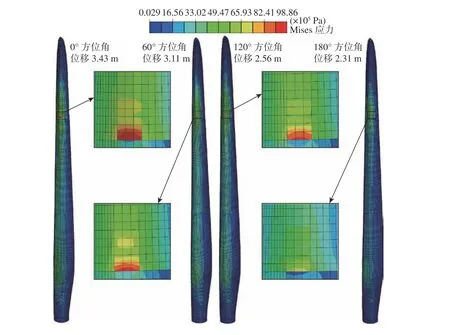
圖13 雙向弱流固耦合葉片應力及葉尖位移Fig. 13 Stress and tip displacement of a blade under two-way weak fluid-structure coupling

圖14為0°方位角下變槳故障葉片前六階屈曲因子和屈曲模態。屈曲因子的物理意義是載荷與其之乘積即為葉片發生屈曲的臨界載荷。從圖中可看出，最小的屈曲因子是一階屈曲因子1.234 5，說明葉片并未發生屈曲。此外，仔細觀察圖14能夠發現，隨著屈曲階數的增加，葉片發生屈曲部位的面積越來越大，且屈曲因子逐漸提升，但實際工程中最關注的是一階屈曲因子，因為一階屈曲發生之后其他階結構屈曲將無意義。此外，其他方位角結構屈曲情況與0°方位角變化趨勢一樣，且隨著方位角增加葉片屈曲越弱，其中180°方位角下變槳故障葉片的一階屈曲因子較0°方位角下的增大20.2%，結構安全性更高。需要說明的是，本文結構側屈曲分析載荷來自雙向弱流固耦合最后一次流固兩次數據交換并計算結束后氣動側的載荷數據。

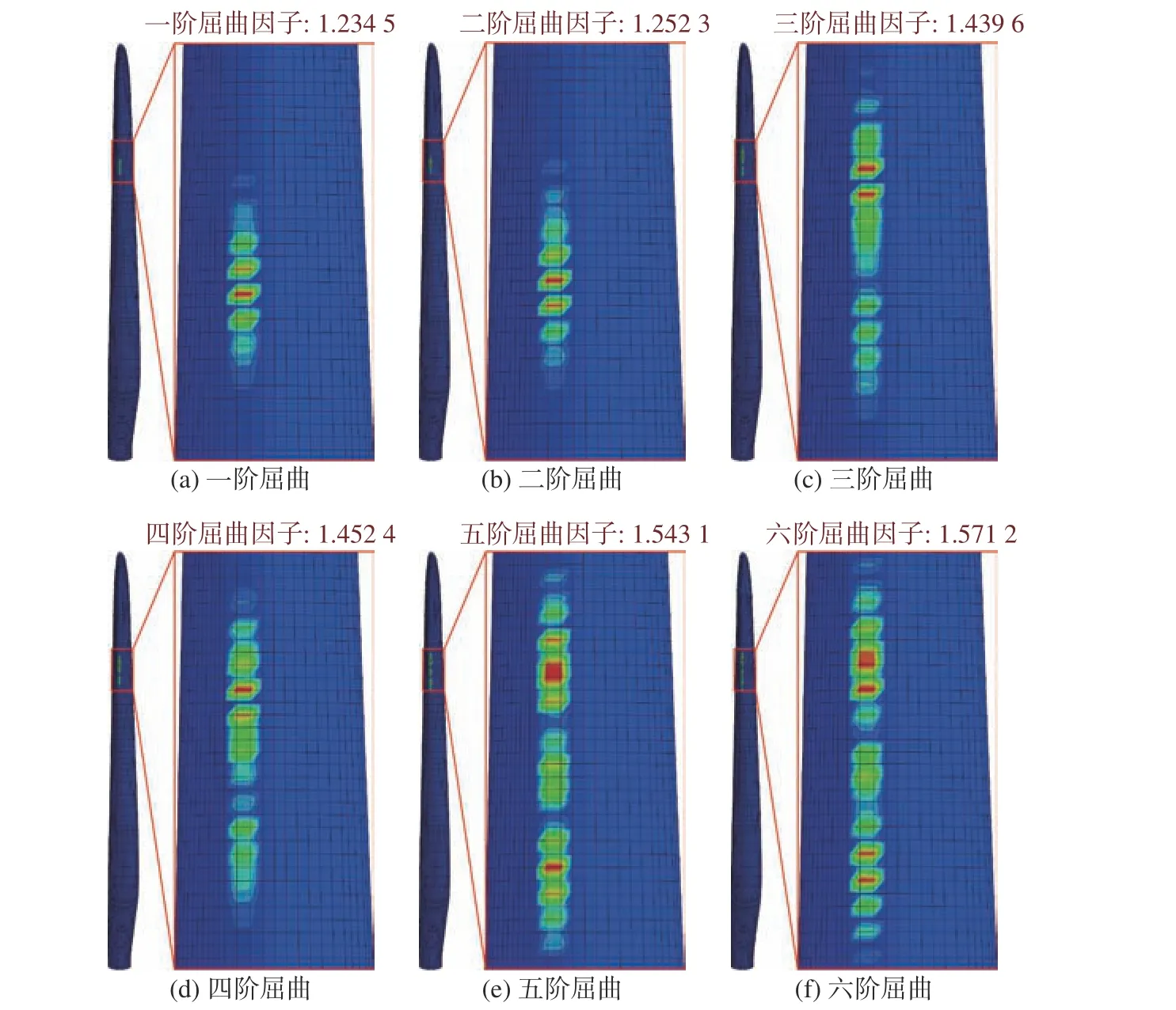
圖14 0°方位角下變槳故障葉片前六階屈曲Fig. 14 The first six order buckling of a blade with pitch fault at 0°azimuth

4 結 論

本文基于計算流體力學方法對NREL 5 MW風力機變槳故障/成功葉片氣動側狀態進行對比分析，并利用雙向弱流固耦合及曲屈分析對典型方位角下變槳故障葉片特征展開研究。主要結論有：

（1）SBM與FRM揮舞力矩和擺振力矩時域序列、頻域特征及渦量場強度和分布差別均非常小或相同，故采用節省大量計算資源的SBM模型可行。

（2）切出風速下變槳故障葉片較變槳成功葉片受載更大，且前者流場尾跡比后者亦更明顯，說明變槳故障葉片從來流風中吸收了更多能量。

（3）180°方位角下變槳故障葉片較0°方位角下變槳故障葉片應力及葉尖位移分別減小29.8%和32.7%，一階屈曲因子增加20.2%。