基于模糊貝葉斯-ANP艦載機出動回收綜合評估

鄧嘉寧, 吳 宇, 許舒婷, 茍進展

(1. 重慶大學航空航天學院, 重慶 400044; 2. 北京航空航天大學航空科學與工程學院, 北京 100191)

0 引 言

航空母艦作為二戰中及戰后新世界的國家級戰略裝備,其具備的軍事功能、科技與經濟功能、外交功能、警察功能等為國家經濟、安全、主權提供了強大保障。其中,艦載機的出動回收能力是衡量航母戰斗力的重要指標,優化艦載機的出動回收流程能夠使得單位時間內艦載機的起降數量得到大幅提升。艦載機在航母上的出動回收流程主要分為以下過程:艦載機起飛前的保障,機庫調運,甲板調運、滑行、起飛,起飛后甲板保障,降落前保障、著艦,回機庫和任務執行后的保障等流程。由于涉及的人員、設備、工序等錯綜復雜,提煉影響艦載機出動回收能力的關鍵性指標將會對提高航母戰斗能力起到重要指導作用。

在艦載機出動回收流程關鍵指標的確立方面已有相關研究。對于艦載機的調運作業,文獻[5]對比了艦載機在甲板上調度的3種模式,即自主滑行、無牽引桿的牽引系統和帶牽引桿的牽引系統,結合智能算法進行仿真,對不同模式的優劣進行了分析。對于艦載機甲板調運作業,文獻[6-7]提出了分層協同規劃結構,建立了協同路徑規劃數學模型,對于艦載機多機協同起飛降落的動態多目標優化問題進行了研究。關于飛行甲板統一調度方面,文獻[8]提出了關于下一代飛行甲板自動化調控輔助設備的原型,該設備基于人的行為準則、認知、行動建模,能夠評估和比較潛在的自動化調控方案,并確定潛在的人機交互問題。文獻[9]將艦載機著艦回收過程中的調度問題抽象為滿足尾流間隔、剩余燃油及跑道復位等約束的隨機規劃模型,提出了基于飛機優先順序指標函數的蒙特卡羅模擬-差分進化搜索的實時調度算法,解決了由于飛機故障、著艦復飛逃逸等因素產生的動態隨機調度問題。為保障艦載機的安全,文獻[10]對艦載機著艦環境進行了研究，在描述甲板環境后,對航母運動進行建模,包括確定性模型和隨機模型，分析了大氣擾動的變化規律,進而設計了水平尾流、橫向尾流和垂直尾流3個組件,集成了艦載機著艦系統。

上述論文對于艦載機出動回收的單個或者多個流程進行了研究,但缺乏對于整個出動回收流程的關注。文獻[11]通過對美國、英國、法國和俄羅斯幾個典型案例的分析,對艦載機出動回收能力的基本概念：出動架次率、飛行日長度、特定任務等進行了研究,提出了衡量出動回收能力指標的主要特征,并從設備、工作人員和環境3個方面出發,分析了影響艦載機出動回收能力的主要因素。同時，文獻[12]通過分析各因素之間的耦合影響度,建立了艦載機航空保障網格化指標體系。其中,指標體系以控制指揮、起飛保障、轉運保障、攔阻著艦、艦面保障和維修支援6個方面為主,建立了相對完善的艦載機航空保障效能評估體系。此外，文獻[13]以美軍航母公開數據為基礎,對其航母艦載機出動回收能力和飛行甲板控制策略進行了研究,采用調度模型臺推演艦載機出動和回收過程,并對航空保障的限制因素進行分析,歸納出保證美軍航母出動架次率的重要因素,進而總結出美軍航母飛行甲板控制策略。

隨著航母國產化進程的加快,上述關于艦載機出動回收的某個或多個環節的研究不能滿足海軍發展的需求,因而對于航母艦載機出動回收全過程中關鍵指標的研究將會對海軍整體戰斗能力的提升起到重要指導和參考作用。本文將基于以上文獻的研究,結合實際情況從人、機、環3個方面出發,以文獻[12]中艦載機保障評價體系為基礎,擴展建立了由頂層指標、子系統層指標和設備層指標組成的描述艦載機出動回收能力的3層指標體系,以便更加詳細具體地研究影響艦載機出動回收能力的關鍵性指標。同時，關于艦載機出動回收能力指標體系的分析方法,普遍使用較多的是面向內部獨立遞階結構的層次分析法(analytic hierarchy process, AHP)和面向內部依存復雜結構的網絡層次分析法(analytic network process, ANP),而由于航母艦載機出動回收流程的復雜性,即在子系統層內的設備層指標之間并非完全獨立,AHP無法準確反映設備層指標的復雜聯系,因此ANP比AHP更加適合。

本文將首先建立航母艦載機出動回收能力評價體系;然后結合三角模糊數和擴展貝葉斯融合法確定指標之間的相互關系,在此基礎上建立用于計算分析的ANP模型;其次通過得到的ANP模型,基于提出的三角模糊數評價尺度標準和模糊數標準化方法,結合歷史實驗數據進行綜合評價;最后進行了多組結果對比分析,驗證了所提方法的有效性。

1 艦載機出動回收評價體系的建立與指標相互關系的確定

在本節研究中,首先建立能夠系統、全面體現艦載機出動回收能力的評價體系;再根據建立好的評價體系設計問卷,專家將根據問卷,基于信心度和關系度,對指標之間的相互關系進行評判,最終評判的結果將決定評價體系中設備層指標的相互關系。

1.1 艦載機出動回收能力評價體系建立

建立艦載機出動回收效能評價體系,將涉及對艦載機保障的各個系統、各個流程進行系統完備的分析。本文重點關注關鍵性的評價指標,建立有序、有效的網絡結構層次評價關系,進而提出能綜合全面體現艦載機保障能力的有效評價體系,形成航母艦載機保障能力決策層向因素層的有效映射。

根據實際作戰需求,以艦載機出動回收能力作為頂層指標;將艦載航空保障系統分為艦載機搭載能力、艦載機起飛保障能力、攔阻著艦保障能力、航空指揮控制能力、艦面保障能力、維修支援保障能力和人員保障能力7個部分的子系統層;位于最底層的為設備層指標,整個艦載機保障評價指標系統的組成如圖1所示。

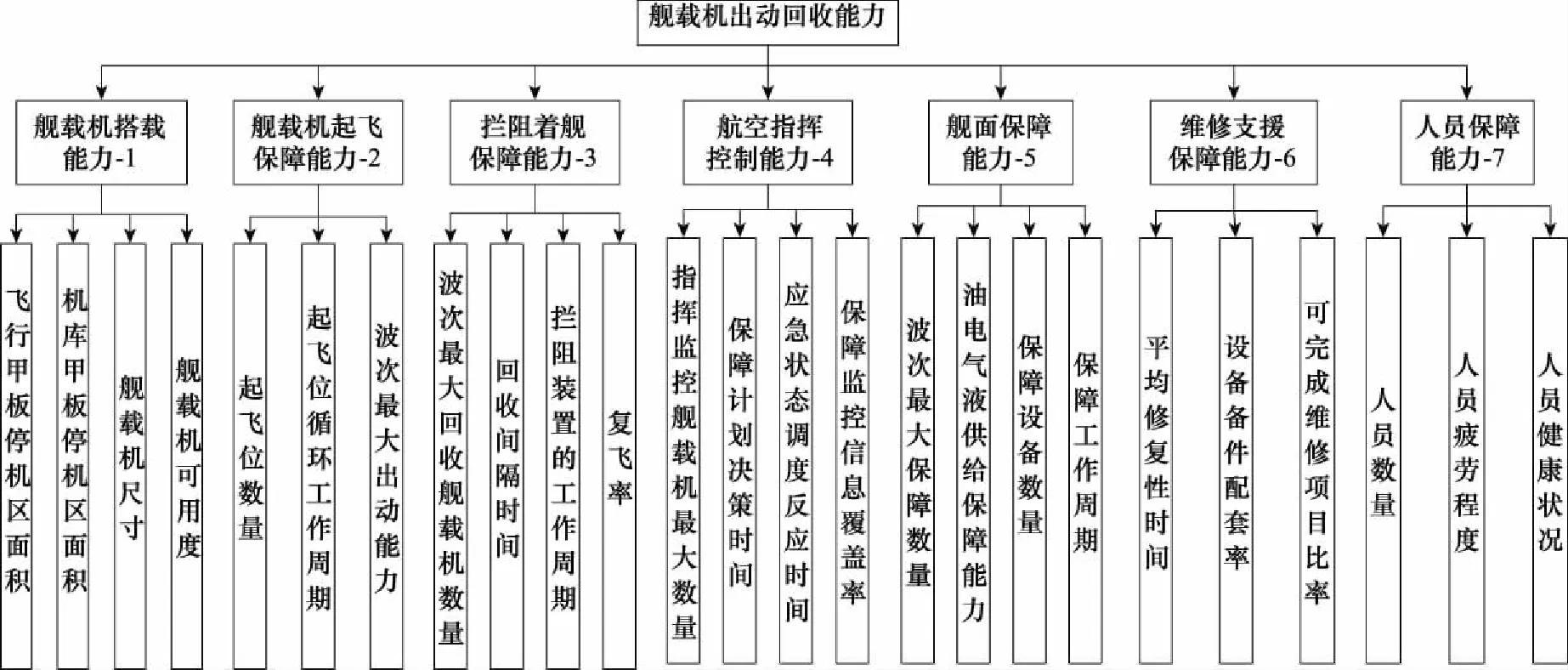
圖1 艦載機出動回收能力評價系統Fig.1 Carrier aircraft’s dispatch and recovery capability evaluation system

1.2 基于三角模糊數的擴展貝葉斯融合法指標關系的確定

在利用ANP對艦載機出動回收能力評價體系進行綜合評估之前,需要對體系內的設備層指標之間的相互關系進行確定,即區分設備層指標之間的因果關系,進而確定設備層指標從屬的子系統層之間的相互關系。

1.2.1 擴展的貝葉斯融合法

在建立了完備的艦載機出動回收能力評價體系之后,需要專家對各底層指標之間的相互關系進行評判打分。基于專家評判打分的結果,采用以貝葉斯決策理論為基礎的擴展貝葉斯融合法進行處理，其中，為描述兩個指標之間的相互關系,引入信心度和關系度(表示為[,])進行綜合評判,其中信心度和關系度均在0到1之間,即:0≤≤1,0≤≤1,根據擴展的貝葉斯融合法有:

(1)

式中:是標準化因子;(=)表示在評判準則下,評價體系中指標與指標之間存在相互關系的概率;表示參與評判的第位專家。

根據式(1)得到的指標間存在的相互關系進行融合分析,建立指標之間相互影響度的判斷矩陣=,,∈(1,),∈[0,1],表示在指標變化下指標對應受影響的程度。對于ANP所需要的網絡化指標評價體系而言,只需要確定指標之間存在關系與否,在本體系中,將指標之間是否存在關系的概率閾值定為05,即:當0≤<05時,=0;當05≤≤1時,=1。當概率為0時表示兩個指標與不存在相互關系,當概率為1時表示兩個指標與存在相互關系,由此得到指標之間是否存在關系的0-1判斷矩陣。

122 三角模糊數評判標準的建立與標準化方法

由于在艦載機出動回收能力評價體系中,各個指標間的相互關系比較復雜,對于復雜關系的評判無法用準確單一的數字進行具體描述。因此,引入模糊判斷語言變量與三角模糊數變化量,對專家在評判時信心度和關系度的具體范圍進行規定,如表1所示。

表1 模糊判斷語言變量及數值表示Table 1 Fuzzy judgment language variables and numerical representation

表1所示的三角模糊數表明了專家在對指標影響關系及自身判斷信心度的大致判斷范圍,為便于后續計算和計算結果的有效性,需要對判斷矩陣里的三角模糊數進行去模糊標準化處理,去模糊化過程如下。

記三角模糊數的范圍:(,,),位專家的評判分別記為:(,),(,),…,(,)。

(1) 專家判斷語言數值信息的三角模糊數標準化

(2)

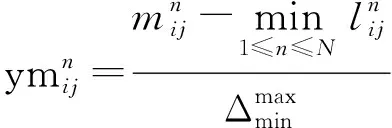
(3)

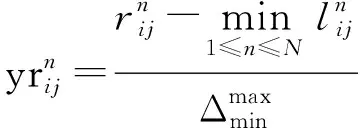
(4)

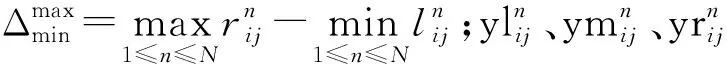
(2) 計算三角模糊數標準化數值的左右限值

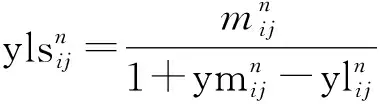
(5)

(6)

式中：yls、yrs分別表示專家的信心度或關系度模糊數標準化過程中的最大最小限值。

(3) 計算三角模糊數標準化數值的總值

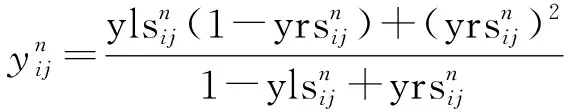
(7)

(4) 計算專家對于指標與指標的信心度或關系度的精確值

(8)

由于其中信心度和關系度均表示專家對于指標相互關系的判斷,且數據結構相同,故均可由式(2)～式(8)處理。可表示各個專家模糊評判值(,)經過去模糊化得出的單一標準化數值(,)。

(5) 根據標準化后的信心度進行歸一化處理

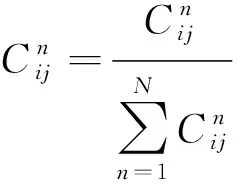
(9)

(6) 利用標準化后的關系度和歸一化處理的信心度根據式(1),確定指標與指標存在相互關系的概率矩陣

(10)

123 建立ANP分析模型

為了建立用于ANP分析的模型,首先需要由多位專家,根據表1的三角模糊數,對所有設備層指標之間的信心度和關系度進行評判;然后再按照式(2)～式(9)進行標準化處理得到標準化數值(,);最后再利用貝葉斯融合法,確定設備層指標之間的相互關系概率矩陣,同時對根據概率閾值進行0-1化處理。

根據得到的指標之間是否存在關系的0-1判斷矩陣,建立的ANP模型如圖2所示。

圖2 艦載機出動回收能力評價模型示意圖Fig.2 Schematic diagram of carrier aircraft’s dispatch and recovery capability evaluation model

在ANP的網絡模型中,子系統層之間的關系由設備層指標決定,如:11→14、21、22、23、41、42、43、44、51、53、54、61、63、71、72,表示指標11的變化會引起箭頭后其他指標的變化。同時，包含上述設備層指標的子系統層之間也存在關系:1→1、2、4、5、6、7,表示艦載機搭載能力-1的變化會引起保障能力-2、航空指揮能力-4、艦面保障能力-5、維修支援能力-6、人員保障能力-7的變化,其中指向自己的箭頭表示同一子系統層內的設備層指標存在相互關系。

2 基于模糊數的多源數據綜合權重確定

在利用ANP進行設備層指標在整個系統中權重占比計算之前,需要根據第12節確定的設備層指標之間的相互關系,基于相關準則尺度標準進行綜合評判,常用的評判準則是經典1～9尺度標準,本文為了貼合人為評判的模糊性和不確定性,采用了一種基于三角模糊數的尺度標準,經去模糊化后,結合歷史實驗數據和專家評判確定最終綜合權重。

2.1 基于三角模糊數的評判標準與去模糊化

在經典ANP中,設備層指標之間和分系統層指標之間的重要性評判普遍采用1～9標度法,為了保證專家的評判更加符合客觀規律,本文采用了如表2所示的基于三角模糊數的評價法。

表2 基于三角模糊數的ANP評判標度Table 2 ANP evaluation scale based on triangular fuzzy number

在以1～9標度法的ANP判斷矩陣中,對角線元素始終為1,并且關于對角線對稱的元素相乘為1,為了保證基于模糊數的判斷矩陣也具有上述特征,在新的判斷矩陣中,對角線元素定為(1,1,1)。按照如表2所示的三角模糊數標度的判斷矩陣,給出一個示例,如表3所示。

表3 三角模糊數標度判斷矩陣Table 3 Judgement matrix of triangular fuzzy number scale

在表3中,第2行第3列中的(4,5,6)表示相比于指標2,指標3明顯重要。

對于ANP判斷矩陣中三角模糊數的去模糊化,需要綜合考慮多個專家的判斷矩陣時,每個專家的判斷矩陣均采用式(2)～式(8)。雖然在進行指標之間重要性評判時未采用第1.2.1節中基于信心度與掌握度的融合貝葉斯法,但對不同專家意見采取了不同的考慮權重,同時配合文獻[33-34]所提式(2)～式(8)采用的模糊數尺度標準,也能避免專家極端分歧產生結果失真的情況。同時，需要對去模糊后生成的判斷矩陣進行一致性檢驗,如果判斷矩陣的平均隨機一致性比例大于等于0.1,則認為該矩陣的一致性是不能接受的,需要組織專家重新進行判斷以滿足一致性要求。

2.2 通過歷史實驗數據確定判斷矩陣

通過收集航母艦載機系統出動回收過程中的相關數據,計算得到不同指標的歷史實驗數據,用于確定兩個指標之間的相對重要度判斷矩陣,設個影響指標的歷史實驗數據為=[,,…,],個被影響指標的歷史實驗數據為=[,,…,],其中對于指標之間的相互關系可采用最小二乘法進行確定,即兩個指標的歷史數據經過一維線性擬合得到關系模型=+,進而可以求得和,兩個指標對應的比例關系為,令=[,,…,]，通過擬合得到的,對兩個需要判斷的指標進行一維線性關系斜率比較,得到歷史實驗數據的判斷矩陣為

(11)

式中:對、取絕對值是為了消除指標之間負相關對于判斷矩陣中出現負數的影響。在ANP中,任意兩個設備層指標或者子系統層指標重要性對比的數值不能為負,若由歷史實驗數據線性擬合得到的斜率和不取絕對值,當其中一個為負數時,由式(11)得到的<0,不滿足判斷矩陣元素大于零的條件,無法進行接下來的權重占比計算,進而無法完成未加權超矩陣的建立。同時,若判斷矩陣中存在負元素,計算得到的權重占比的數值存在負數,不符合實際。

由式(11)產生的判斷矩陣不符合1～9標度判斷標準,可能會造成ANP的極限超矩陣不收斂,因此將判斷矩陣進行標準化處理:

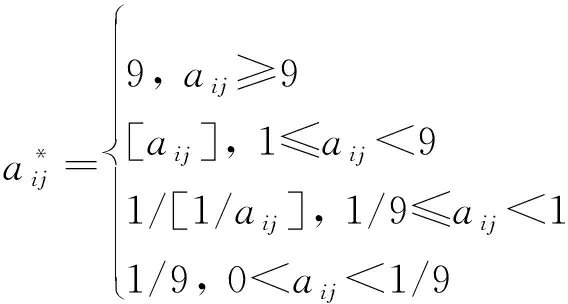
(12)

2.3 專家評估與歷史實驗數據融合

通常在對設備層指標之間或者子系統層指標之間根據ANP判斷尺度標準進行評判時,有兩種途徑:一是通過收集專家基于經驗略帶主觀性的判斷矩陣,二是通過對采集的歷史實驗數據對某些指標進行定量分析后,確定指標之間的關聯度,從而構建基于歷史實驗數據的判斷矩陣。為了使得到的指標判斷矩陣更加準確,將具有主觀性的基于專家經驗的判斷矩陣和客觀性更強的歷史實驗數據得到的判斷矩陣進行融合處理,同時根據不同判斷矩陣的來源、重要性、權威性,設置不同的參考權重。

以融合兩個判斷矩陣為例,設=()×,=()×為兩個不同的判斷矩陣,和為和分別所占的比重且+=1,定義判斷矩陣、融合后的判斷矩陣為:

(13)

對于融合專家評估和歷史實驗數據所得到的判斷矩陣進行一致性比例判斷,若符合一致性要求,將判斷矩陣進行和法權重計算:

(14)

2.4 ANP權重計算

241 子系統層指標之間權重超矩陣

由式(14) 可以得到關于多評價源的綜合判斷矩陣權重列向量,將其作為子系統層指標之間權重超矩陣子列向量,得到權重超矩陣;指標集間權重超矩陣表示了指標集之間的權重占比(列和為1),指標集間權重超矩陣將為指標間未加權超矩陣提供加權處理。

為了之后與指標之間的超矩陣所對應,將擴展為如表4所示形式。

表4 擴展后的子系統層指標之間權重超矩陣Z25×25Table 4 Extended weight super matrix Z25×25 between the indicators of subsystem layer

2.4.2 設備層指標之間加權超矩陣

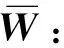
(15)

式中：是第241節中表4所示擴展后的子系統層指標之間權重超矩陣。

243 極限超矩陣與權重

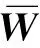
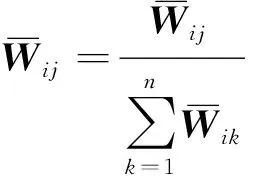
(16)

3 仿真算例研究

本文采用模糊ANP方法與經典ANP方法進行對比,從采用的尺度標準及融合歷史實驗數據與否兩個方面進行算例仿真對比分析,模糊ANP方法與經典的ANP方法的主要特點如表5所示。(對于本文所涉及的程序計算,采用spyder進行計算:python版本3.8.0)。

表5 經典ANP與模糊ANP比較Table 5 Comparison between classical ANP and fuzzy ANP

3.1 融合專家評價和歷史實驗數據方法的驗證

為了驗證專家評價結果和歷史實驗數據所得到數據的一致性,將融合專家評價與數據同僅考慮專家評價的最終權重占比排序進行對比分析,得到的權重具體占比如表6所示。其中，權重1和排序1是綜合了專家和數據得到的結果,權重2和排序2是只有專家評價的最終結果。

表6 艦載機出動回收能力評價體系指標權重排序(融合歷史實驗數據與否)Table 6 Indicator weight ranking of carrier aircraft’s dispatch and recovery capability evaluation system (Combined with historical experimental data or not)

對表6中的數據進行分析,可得到如下結論:

(1) 排序靠前的關鍵性指標有起飛位數量和波次最大出動能力,排序靠后的非關鍵性指標有人員疲勞程度和復飛率,以上4個底層指標在整個艦載機出動回收能力權重占比排序中存在差異,而其他指標的權重占比無差異;并且兩種方法關于子系統層的權重排序無差異,說明綜合專家評判與融合專家和數據的評判大致相符。

(2) 關鍵性指標起飛位數量和波次最大出動能力存在差異,說明在未融合數據僅靠專家主觀評判存在一定程度的結果失真,為了更好地體現結果的客觀真實性,需要綜合考慮專家意見和歷史實驗數據。

(3) 在艦載機出動回收能力評價體系指標權重排序中,排在前五的分別是:應急狀態調度反應時間、波次最大出動能力、起飛位數量、波次最大保障數量、波次最大回收艦載機數量。以上5個指標分別涉及了航空指揮控制能力、艦載機起飛保障能力、艦面保障能力、攔阻著艦保障能力4個方面。并且由文獻[11]可知，在戰時緊急狀態下,應急狀態下調度反應時間至關重要,同時起飛位數量，最大的出動、保障、回收能力也對于艦載機的出動回收能力影響極大,關注并改善這些因素對于提升艦載機出動回收能力將有顯著效果。

3.2 模糊ANP與經典ANP對比分析

為了驗證模糊ANP相對于經典1～9尺度標準ANP的合理性,采用模糊標度進行評判的底層指標最終權重排序和采用1～9尺度標準評判的結果進行對比分析,得到的權重具體占比如表7所示。其中，權重3和排序3是采用模糊標度得到的結果,權重4和排序4是采用1～9尺寸標度得到的最終結果。

表7 艦載機出動回收能力評價體系指標權重排序(模糊ANP與經典ANP)Table 7 Indicator weight ranking of carrier aircraft’s dispatch and recovery capability evaluation system (fuzzy ANP and classical ANP)

在表7中,設備備件配套率、波次最大回收艦載機數量,以及艦載機可用度和飛行甲板停機區面積,上述4個設備層指標的排序存在差異,其他的指標排序無變化。同時，子系統層權重排序也無差異,說明基于三角模糊數的ANP具有和經典ANP具有一致的合理性。

4 結束語

科學評價艦載機出動回收效率對于提升航母艦載機系統戰斗力具有重要意義。本文首先根據文獻和實際情況建立了綜合考慮人員、設備、環境的艦載機出動回收能力評價體系;然后根據建立的評價體系設計問卷,基于三角模糊數,由綜合專家信心度和掌握度的擴展融合貝葉斯法確定設備層指標之間的相互聯系;最后通過基于三角模糊數的尺度標準,對子系統層指標之間、設備層指標之間進行重要性評判,經由計算出設備層指標權重占比,完成算例的仿真研究。在確定指標相互關系時,對于提出的基于三角模糊數的擴展貝葉斯融合法,在信心度和關系度對于判斷的相互約束與相互補充下,比經典ANP中單個數值進行評判更加符合人為主觀判斷的模糊性和不確定性。同時，基于三角模糊數的ANP評價尺度標準,相比于經典ANP準確數字1～9尺度標準,判斷更具客觀性。改進的模糊ANP與經典ANP分析得到的權重無明顯差異,也表明了本文所采用方法的相對正確性。此外，在評判中加入歷史實驗數據,與專家評判相融合后,使得評判結果比只靠專家評判的經典ANP更具客觀性。綜上，本文采用的模糊ANP更加適合艦載機出動回收效率的評估。