橢圓球面波信號Wigner-Ville分布顯式漸近求解方法

王紅星 趙樂源* 陸發平 劉傳輝 康家方

①(海軍航空大學 煙臺 264001)

②(山東省信號與信息處理重點實驗室 煙臺 264001)

③(中國人民解放軍 91206部隊 青島 266000)

1 引言

橢圓球面波函數(Prolate Spheroidal Wave Functions, PSWFs)作為一類特殊的非正弦函數，具有雙完備正交、時域波形嚴格奇偶對稱、時間帶寬積與頻譜靈活可控、能量聚集性最佳的帶限函數集等優良特性[1,2]。基于PSWFs信號的非正弦波通信可直接在時頻域2維空間進行信號波形設計，具有信號波形設計靈活性、高能量聚集性以及高頻譜效率等諸多優良特性，非常符合新一代通信系統的信號波形設計需求，是一種極具有應用潛力和推廣前景的通信新體制[3—5]。

在利用PSWFs信號進行信息加載、檢測、濾波等信號處理的過程中，都會涉及PSWFs信號基礎特性的運用[6]。其中，時頻分布特性反映PSWFs信號頻率隨時間變化情況以及時頻能量分布情況，對于PSWFs信號的檢測具有重要意義。傳統的PSWFs信號的檢測，大都沿用基于正交性的相關檢測[7,8]，在信道條件惡劣、正交性被破壞時，檢測效果較差。而根據PSWFs信號時頻分布特性，從時頻域上提取有用PSWFs信號時頻特征參量用以檢測，有望突破正交性的束縛，提升檢測性能。

為進一步挖掘PSWFs信號的時頻特性，文獻[9]引入Wigner-Ville分布(Wigner-Ville Distribution, WVD)，分析了PSWFs信號WVD交叉項的時頻分布規律；文獻[10]引入平滑Wigner-Ville分布(Smoothed Wigner-Ville Distribution, SWVD)，分析了交叉項抑制情況下的PSWFs信號時頻分布；文獻[11]引入短時傅里葉變換(Short Time Fourier Transform, STFT)、S變換(Stockwell Transform, ST)等時頻分析工具，分析了線性時頻分析方法下的PSWFs信號的時頻特性。研究發現，相對于STFT, S變換等時頻分析方法，WVD的時頻分辨率更高，且不受窗函數的影響，能夠為PSWFs信號時頻檢測提供更為精確的時頻特征參量[12]。此外，WVD能夠反映信號間相互作用的規律，已廣泛應用于一些重要信號的檢測[13,14]。

然而，由于PSWFs信號無閉式解析解，無法直接根據顯式閉式表達式分析其時頻特性。前期關于PSWFs信號時頻特性的研究都是采用數值仿真分析方法進行的，求得的PSWFs信號時頻分布結果存在誤差且誤差不可控，PSWFs信號原有的奇偶對稱性在時頻分布結果中已經不再保持。數值仿真處理使得信號全部采樣點都參與運算，導致后續信號處理復雜度較高，而信號時頻分布的對稱性將在降低信號處理復雜度方面發揮重要的作用[15]。若能產生一種誤差可控的PSWFs信號WVD顯式漸近表達式，且能保持信號原有的對稱特性，根據表達式進行時頻特性定量分析甚至時頻檢測，將會是一個更為有效的辦法。目前對于PSWFs信號時頻顯式漸近表達式及其求解方法的研究，尚未見國內外相關文獻報道。

Legendre多項式作為一種完備的正交多項式，在時域上線性疊加可逼近PSWFs信號[16]；其具有天然的奇偶對稱性，且線性運算后對稱性保持不變，使得逼近的PSWFs信號將保持嚴格奇偶對稱。基于上述思路，本文將Legendre多項式與WVD相結合，提出一種PSWFs信號WVD顯式漸近求解方法。本方法能夠根據誤差要求，生成所需階數的Legendre多項式WVD自項、交叉項，進而與對應的WVD-Legendre系數相乘后線性疊加，獲取PSWFs信號WVD顯式漸近表達式。理論與數值仿真結果表明，所提方法產生的漸近表達式能夠滿足誤差要求，實現誤差可控，且能夠有效保持信號原有的對稱性。此外，在相同采樣點數情況下，相對于PSWFs信號數值解的WVD，所提方法得到的PSWFs信號WVD頻域分辨率更高，為根據顯式漸近表達式進行時頻特性定量分析甚至時頻檢測提供了有效途徑。

2 PSWFs信號WVD顯式漸近表達式的導出

為導出PSWFs信號WVD顯式漸近表達式，下面將Legendre多項式和WVD相結合，具體為將基于Legendre多項式的PSWFs信號顯式表達式與PSWFs信號WVD表達式相結合，并簡要分析表達式積分限。

文獻[18]對PSWFs函數的Legendre多項式表達給出了詳細的理論證明，基于Legendre多項式的PSWFs信號顯式表示為

式(5)即為基于Legendre多項式的PSWFs信號的WVD顯式表達式。

在實際應用中，式(5)歸一化Legendre多項式的自項、交叉項階數無法取到無窮，需要控制漸近階數K，求解一定誤差ε下的PSWFs信號WVD顯式漸近表達式。因此，PSWFs信號在漸近階數為K時，WVD顯式漸近表達式可表示為

3 WVD-Legendre系數與漸近階數的求解

3.1 WVD-Legendre系數求解

PSWFs信號與Legendre多項式都具有嚴格奇偶對稱性，其奇偶對稱性與階數有關[1]。階數為偶數時，PSWFs信號與Legendre多項式都為偶對稱；階數為奇數時，PSWFs信號與Legendre多項式都為奇對稱。由式(8)可知，當Legendre多項式與PSWFs信號奇偶性不同時，兩者相乘后為奇函數，經過積分后，Legendre多項式系數為0，故只需求解奇偶性相同的Legendre多項式及其對應系數即可。

對于任1階Legendre多項式Pk(t)，滿足微分方程

3.2 矩陣A階數及漸近階數求解

由式(7)可知，所提方法產生的PSWFs信號WVD顯式漸近表達式的精度與所需Legendre多項式的漸近階數K有關，階數越高，逼近精度越高；同時，還需要求解矩陣A的階數M。下面通過分析PSWFs信號WVD與Legendre多項式自項、交叉項的相關值，來求解矩陣A的階數M和漸近階數K，并給出最終的PSWFs信號WVD漸近表達式。

這一結論對矩陣A階數M及漸近階數K的求解具有理論指導作用，不足是該界限對于漸近階數K而言更為寬泛，進而使漸近表達式求解復雜度增加。

(1)矩陣A階數求解。根據Moyal’s公式[20]，Legendre多項式的WVD自項與PSWFs信號的WVD自項的內積為

(2)漸近階數求解。理論上，所需Legendre多項式的WVD自項、WVD交叉項的階數K應該與矩陣A的階數M一致，即K=M。在實際工程應用中，為進一步降低空間復雜度，需在誤差允許的范圍內，減少Legendre多項式的儲存階數。

由此可以得到Legendre多項式的WVD自項、WVD交叉項的漸近階數K應滿足

由式(8)可知，奇偶性不同的PSWFs信號與Legendre多項式互相關值為0，故可對奇、偶階PSWFs信號WVD漸近表達式分開求解，以降低計算復雜度。此外，為保證Legendre多項式的WVD自項、交叉項與PSWFs信號的WVD互相關值都小于ε2，應滿足Legendre多項式大于K。故在漸近階數為K時，PSWFs信號WVD顯式漸近表達式可表示為

4 數值仿真驗證

本節結合數值仿真，主要從漸近階數驗證、時域頻域對稱性、時域頻域分辨率3個方面對所提方法進行驗證，給出由所提方法得到的PSWFs信號WVD在誤差控制、時域波形以及頻域波形的對稱性、時域頻域分辨率等方面，與基于數值解的PSWFs信號WVD[11]的對比分析結果。具體系統參數設置如表1所示，其中，基于數值解的PSWFs信號WVD方法參數設置與本文所提方法參數設置一致。

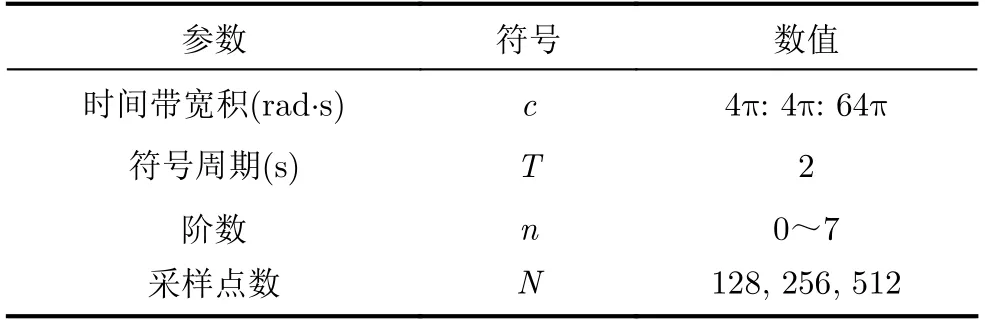
表1 PSWFs信號仿真參數設置

4.1 漸近階數驗證

WVD-Legendre系數能夠反映Legendre多項式WVD自項、交叉項與PSWFs信號WVD的相關程度，進而反映Legendre多項式WVD自項、交叉項漸近PSWFs信號WVD的誤差大小。下面結合數值仿真，給出不同階PSWFs信號對應的WVD-Legendre系數，并驗證漸近階數K的有效性。由于Legendre多項式WVD自項與交叉項所需的階數K是一致的，下面僅分析Legendre多項式WVD自項對應的系數。

時間帶寬積為8π rad·s的PSWFs信號對應的WVD-Legendre系數如圖2所示。由圖2可知，在ε=10—3即ε2=10—6時，漸近階數K取18；根據本文所提方法可知，此時矩陣A階數M取149，漸近階數K=18＜149。而若根據文獻[19]，漸近階數K與矩陣A階數M都要取149。故在實際求解過程中，文獻[19]給出的界限更為寬泛，使得求解復雜度大大增加。

基于數值仿真的方法需要先數值求解產生PSWFs信號，然后經過離散WVD。此過程存在PSWFs信號求解誤差與舍入誤差。對于PSWFs信號求解誤差，參照文獻[21]，采用Legendre多項式逼近PSWFs信號的方法。給定誤差閾值ε，PSWFs信號求解所需的Legendre多項式階數為m。然后經過離散WVD，將存在舍入誤差，且根據離散WVD基本原理，WVD需要信號自相關后積分，此時的誤差將增大且大于ε。

通過上述分析可知，基于數值仿真的PSWFs信號WVD均采用數值解進行處理，存在求解誤差、舍入誤差，誤差計算復雜度高。本文所提方法采用直接控制Legendre多項式WVD逼近PSWFs信號WVD的方式，通過控制漸近階數實現誤差控制。并結合圖2表明，本文所提方法求得的漸近表達式既可滿足誤差要求、實現誤差可控，又可有效降低空間復雜度。

4.2 WVD時域、頻域對稱性

WVD具有時間、頻率邊緣性，對WVD沿頻率軸積分，可得信號瞬時能量分布；對WVD沿時間軸積分，可得信號能量譜密度，故信號時域、頻域單一能量域的性能能夠直接反映時頻域的性能。

對稱均方誤差(Mean Square Error, MSE)[15]可用來判斷信號的對稱性，根據文獻[15]，MSE值越小，對稱性越好。PSWFs信號時域MSE如圖3(a)所示。從數值仿真結果可知，基于數值解的PSWFs信號WVD，其時域MSE始終大于0，而本文所提方法產生的WVD時域MSE始終為0。這表明基于數值解的PSWFs信號WVD時域對稱性缺失，而本文所提方法能夠保持PSWFs信號WVD在時域上嚴格對稱。

PSWFs信號頻域MSE如圖3(b)所示。從數值仿真結果可知，基于數值解的PSWFs信號WVD，其頻域MSE始終大于0，而本文所提方法產生的WVD頻域MSE始終為0。這表明基于數值解的PSWFs信號WVD頻域對稱性缺失，而本文所提方法能夠保持PSWFs信號WVD在頻域上嚴格對稱。

4.3 WVD時域、頻域分辨率

本文所提方法通過對時間、頻率等間隔取點，得到PSWFs信號的WVD。基于數值解的PSWFs信號WVD，是PSWFs信號數值解經過離散WVD得到的，整個過程都是離散化處理。其中，基于DPSS的數值解PSWFs信號vn(t)方法，可用于快速產生PSWFs信號數值解，下面將其作為對比對象，其WVD表示為

時間帶寬積為4π的0階PSWFs信號的時頻分布如圖4所示，其中圖4(a)—圖4(c)為基于數值解的PSWFs信號WVD圖，圖4(d)為本文所提方法得到的PSWFs信號WVD圖。由數值仿真結果可知：

(1)在信號采樣點數一致的情況下，即圖4(b)與圖4(d)，基于數值解的PSWFs信號WVD時頻柵格[17]時間長度為0.008 s，頻率長度為0.2 Hz；而本文所提方法得到的PSWFs信號WVD時頻柵格時間長度為0.008 s，頻率長度為0.025 Hz。這表明在信號采樣點數一致的情況下，本文所提方法得到的PSWFs信號WVD和基于數值解的PSWFs信號WVD在時域上具有一樣的分辨率，但在頻域上本文所提方法分辨率更高。

(2)從圖4(a)—圖4(c)，采樣點數逐漸增加，基于數值解的PSWFs信號WVD時頻柵格時間長度逐漸減小，頻率長度保持不變。這表明通過增加采樣點數，可以提高基于數值解的PSWFs信號WVD時域分辨率，但無法提高頻域分辨率，與理論分析一致。

(3)基于數值解的PSWFs信號WVD與本文所提方法得到的PSWFs信號WVD，時頻能量密度具有一致的變化趨勢。如0階PSWFs信號，由時頻中心到時頻區間端點，其時頻能量密度逐漸降低。

需要注意的是，由于PSWFs具有高時頻能量聚集性，圖4只給出了其在有限時頻區域內的圖像，實際上圖4(a)—圖4(c)中N×N個采樣點所占的時頻區域要大于圖4(d)給出的時頻區域。

通過上述分析可知，所提方法求得的漸近階數能夠始終滿足誤差要求，驗證了本文所提方法的有效性。同時，相對于基于數值解的PSWFs信號WVD，本文所提方法求得的PSWFs信號WVD能夠有效保持PSWFs信號原有的時域、頻域的對稱性，且頻域分辨率更高。

5 結束語

原PSWFs信號時頻特性分析是以PSWFs數值解為處理對象，無法給出表達式，且誤差不可控，難以做深入的定量分析；此外，數值仿真得到的PSWFs信號WVD對稱性難以保持。針對上述問題，本文提出一種PSWFs信號WVD顯式漸近求解方法，本方法除能夠解決上述問題外，還為根據漸近表達式分析PSWFs信號時頻特性提供了有效途徑。同時，能夠為PSWFs信號時頻特性的應用奠定理論基礎。如根據本文所提方法產生的漸近表達式，通過提取PSWFs信號特定時頻區域內的特征參量進行檢測，有望實現信噪比的提升，進而提升檢測性能；并且，根據漸近表達式的對稱性，只取一半信號用于檢測，可在檢測性能保持不變的前提下大幅降低信號處理復雜度，這也是課題組下一步所要研究的方向。