子通道程序對PSBT空泡分布實驗計算的不確定性量化分析

張俊濤， 劉曉晶， 張滕飛， 柴 翔

(上海交通大學 核科學與工程學院，上海 200240)

1989年美國發布管理導則RG 1.157[1]，允許在應急堆芯冷卻系統分析中使用最佳估算程序.出于安全考慮，最佳估算程序必須與不確定性分析相結合，以判斷計算與實際情況之間的差異.截至目前，國際上已有多種不同的不確定性分析方法，例如程序比例、適用性和不確定性分析方法(CSAU)[2]、德國核安全中心方法(GRS)[3]、基于精度外推的不確定性方法(UMAE)[4]、先進統計學處理的不確定性方法(ASTRUM)[5]等.這些不確定性分析方法大體可以分為兩大類，一類是基于輸入參數不確定性的傳遞，另一類是基于輸出結果不確定性的外推[6].基于輸入參數不確定性傳遞的統計性方法的研究和應用相對更成熟和廣泛，如在由經濟合作與發展組織(OECD)發起的不確定性研究項目“最佳估算方法-不確定性和敏感性分析”階段V中，14個參與者中有12個采用輸入不確定性傳遞的方法[7].

基于輸入參數不確定性傳遞的方法需要知道輸入參數的不確定性.然而，大多數熱工水力程序都沒有提供關于輸入參數不確定性的足夠信息，尤其是對于某些無法通過實驗直接測量的輸入模型參數，通常通過專家判斷來進行量化.目前一些取代專家判斷的評估方法被陸續提出，如比薩大學開發的基于快速傅里葉變換的方法(FFTBM)[8]，法國開發的輸入參數經驗確定方法(DIPE)[8]和模型參數不確定性計算方法(CIRCé)[9]，韓國原子力研究院開發的通過數據同化進行模型標定方法(MCDA)[10].李冬[11]對CIRCé方法可評估參數有限和MCDA方法求解非線性問題耗時過長這兩個缺點進行了改進；Xiong等[12]開發了一種優化的最佳估算加不確定性分析方法，該方法包含了一個結構化的模型不確定性量化方法.

子通道程序已被廣泛應用于堆芯熱工水力分析，相較于計算流體力學(CFD)，子通道分析消耗的計算資源更少，能夠快速提供分析所需的熱工參數.由于子通道程序對于物理模型存在一定簡化假設以及數值計算誤差等因素的影響，程序直接計算出的結果存在一定的不確定性，而目前針對子通道程序的不確定性分析還較少.本研究使用基于輸入參數不確定性傳遞的統計學方法，利用期望最大化的思想來反推輸入模型參數不確定性的分布，對子通道程序COBRA-IV 的計算進行不確定性量化分析.

1 不確定性量化分析方法

不確定性分析方法包括對影響計算程序結果的所有不確定性因素的確認和描述，并用統計學方法將這些不確定性因素整合得到輸出結果的總體不確定性，其一般過程如圖1所示.首先從眾多輸入參數中選取對計算結果影響較大的輸入參數；其次量化這些輸入模型參數的范圍或不確定性分布；再次通過蒙特卡洛抽樣或拉丁超立方抽樣對這些輸入參數進行抽樣，并將這些抽樣的輸入參數輸入子通道程序進行計算；最后對大量目標參數值進行統計，以得到輸出目標參數的不確定性.其中，輸入參數不確定性的確定和對輸入參數進行抽樣是關鍵步驟.

1.1 輸入模型參數不確定性量化

在分析過程中, 認為輸出不確定性y是真實值yr與程序計算值yc之間的誤差.實際可以得到的數據是實驗值ye與對應的程序計算值yc，兩者之差可以表示為

yw=ye-yc=(ye-yr)+(yr-yc)=e+y

(1)

式中：e=(ej),j=1, 2，…,J為實驗誤差，其中J為樣本點數.

一般來說，模型參數的不確定性分析通常要確定模型參數基準值的無量綱乘數，記為k=(ki),i=1, 2, …,p，其中p為模型參數的個數；將待評估的模型參數不確定性記為x=(xi),i=1, 2, …,p.一般情況下，ki與xi存在以下關系：

(2)

因此可以采用ki=exi來表示模型參數系數和不確定性之間的轉化關系[8].

輸入模型參數不確定性x和輸出不確定性y之間的傳遞關系可簡化為

y=h(x,u)

(3)

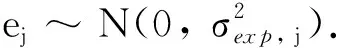
近似認為x與y之間為線性關系，得到

yw=Sxx+Suu+e

(4)

式中：Sx和Su為樣本點對應待求參數的敏感性矩陣，敏感性矩陣中的偏導數可以通過有限差分法求得[11].

當存在數據缺失問題時，期望最大化(EM)算法是極大似然估計的一種常用迭代算法.但是實際計算過程中EM算法一般迭代次數過多，收斂較慢，因此使用EM算法的改進算法，即ECME算法[13]進行計算.

將x的均值和方差記為μx和Cx，即待求參數，統一記為θ={μx,Cx}.完整數據的似然函數表示為L(θ;x1,x2, …,xJ,yw)，簡化表示為[11]

L∝

(5)

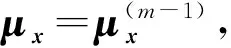
(6)

(7)

式中：ywi為yw的第j個分量.最后最大化似然函數，可以得到

(8)

由于以上是基于正態分布假設的，所以為了證明結果的可靠性需要進行假設檢驗.對殘差進行檢驗，對于每個實驗樣本點，殘差為

(9)

如果殘差服從標準正態分布，則說明正態分布假設成立[8].

為測試該方法的可靠性，建立簡單的數學模型對該方法進行測試.在測試中給定70個樣本點，令已知分布的輸入參數不確定性u的維度為1，待評估的模型參數不確定性x的維度為2，敏感性系數由均勻分布U(5, 50)得到，已知分布參數服從u1～N(1.5, 0.42)，認為實驗誤差為ej～N(0, 0.052)，用于生成yw的真實分布滿足x1～N(-0.6, 0.32),x2～N(1.2, 0.22)，然后根據這些數據反推x的均值和方差，其計算結果如表1所示.可知，計算結果與真實值比較接近，相對誤差不超過11%.

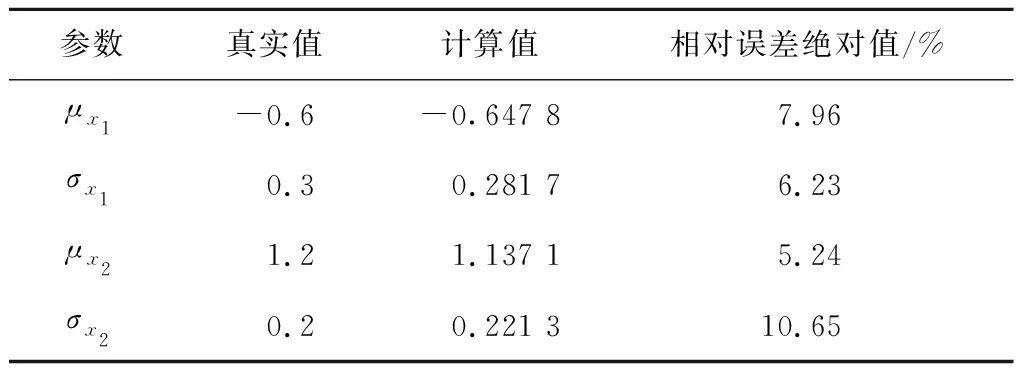
表1 評估所得參數與真實值的比較Tab.1 Comparison of evaluated parameters and real values

1.2 輸入參數抽樣

不確定性的正向傳遞可以通過蒙特卡洛抽樣進行.對確定的所有重要輸入參數同時抽樣，根據次序統計理論，抽樣數目只與輸出結果的容忍區間以及置信水平有關.滿足特定容忍區間的最小抽樣數目由Wilks公式[14]確定，在雙側容忍區間的情況下，其形式為

β=1-γZ+Z(1-γ)γZ-1

(10)

式中：β為置信水平；γ為概率；Z為最小樣本數目.對于統計方法，美國核管會(NRC)建議采用95%的置信水平，不確定性評估必須證明在β=95%時，95%的計算結果(容忍區間)在安全裕度內[15].因此，令β=γ=95%，對于雙側容忍區間可得Z=93，即抽樣計算93次后即可滿足“95/95準則”, 得到的最大值和最小值可以認為是雙95%置信區間的上下界.

2 PSBT空泡份額棒束基準

壓水堆子通道和棒束實驗(PSBT)是2010年發布的一套基準，主要用于驗證現有子通道和計算流體力學程序模擬流體在單管和棒束的空泡份額、含氣率以及偏離泡核沸騰(DNB)等.本研究計算對象為PSBT基準一階段穩態棒束空泡份額分布問題.表2為本文計算涉及的3種組件具體參數[16].其中，B5和B6組件的徑向功率分布場為類型A，如圖2(a)所示；B7組件的徑向功率分布為類型B, 如圖2(b)所示.

圖3為實驗組件截面圖和子通道的具體劃分情況.實驗數據為位于距離加熱底端 2 216、2 669、3 177 mm共3個軸向位置的4個中心子通道的空泡份額平均值.在距離加熱底端2 216 mm的底端測量點的空泡份額較低，空泡聚集在受熱表面，因此實驗確定的空泡份額將低于實際的空泡份額，具有較大誤差.對此，僅選取 2 669、3 177 mm 兩個軸向位置的測量值.根據計算，所選用穩態實驗工況的數據范圍為壓力7.36～14.71 MPa、質量流量1 380.6～2 288.9 kg/(m2·s)、加熱功率 1 920～3 536 kW、入口溫度173.5～287.8 ℃.共選取30組工況，并從中選取25組工況進行輸入模型參數的不確定性量化，利用另外5組對計算得到的不確定性分析結果進行評估，以驗證計算結果的有效性.

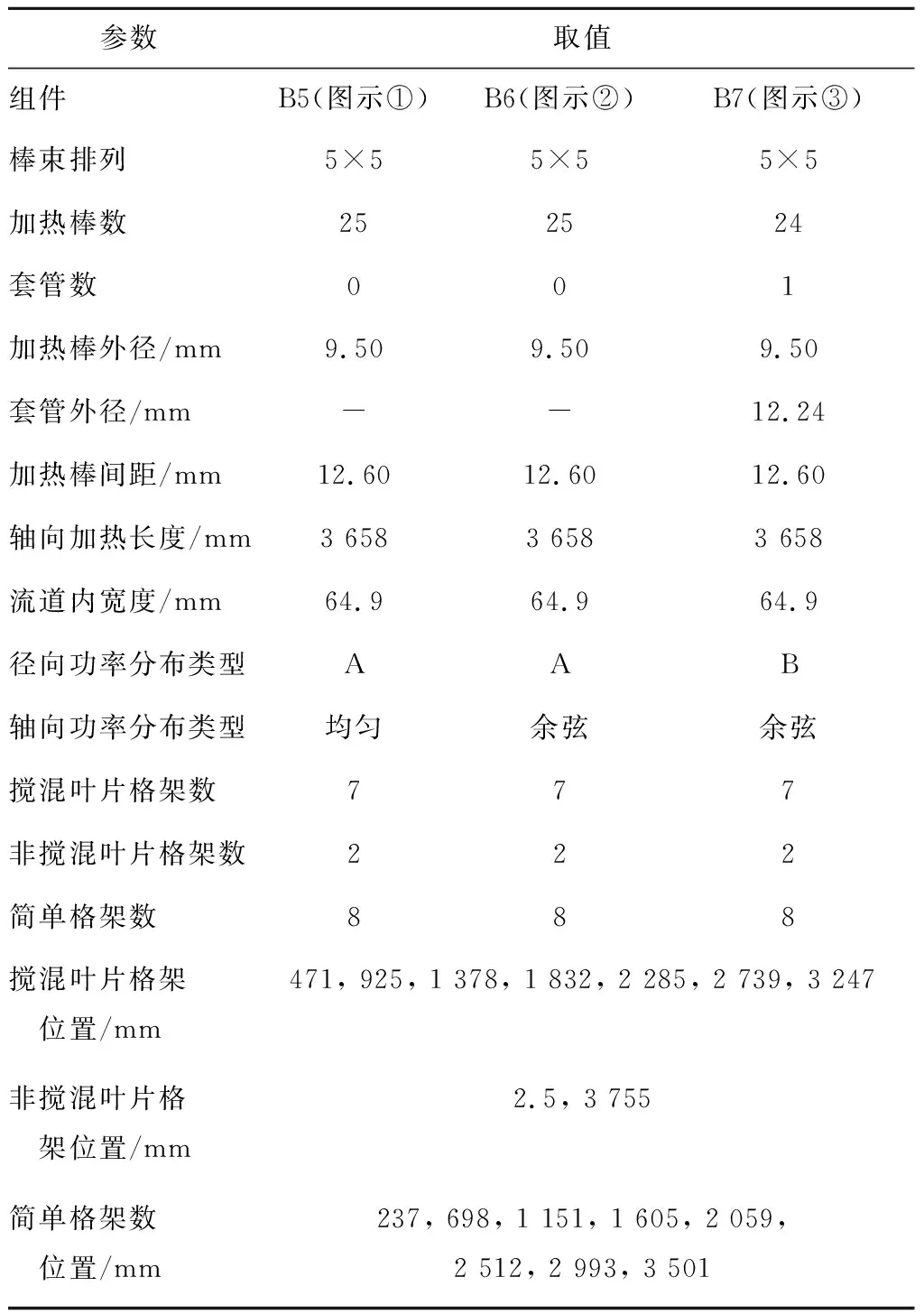
表2 組件參數Tab.2 Parameters of assemblies

①②③

從邊界條件和計算模型兩方面分析影響空泡份額分布的因素.對于邊界條件，PSBT基準報告中給出了邊界條件的測量精度，參照文獻[17]的處理方式：壓力、入口溫度、質量流量、熱流密度的不確定性的分布均為均值為0的正態分布，其標準差依次為0.333%、0.133%、0.5%、0.333%.

在子通道程序的計算過程中所選的重要模型和參數如表3所示.空泡份額模型采用滑移模型，滑速比可以設置.根據最小熵增原理[18]，在14 MPa下的滑速比計算結果為1.86，但是一般情況下計算值比大多數的實驗值偏高[19]，而最典型的單相流模型是均相模型，其把兩相流體看成某種單相混合物流體，認為氣相與液相之間不存在相對速度，即滑速比為1，因此滑速比基準值最終取1.2.湍流交混模型中需要給定湍流交混系數，湍流交混系數主要與幾何尺寸、棒束排布方式、流體類型以及雷諾數(Re)范圍有關，根據與計算工況相近的Castellana等[20]的實驗所得湍流交混系數關系式，取湍流交混系數的基準值為0.008.

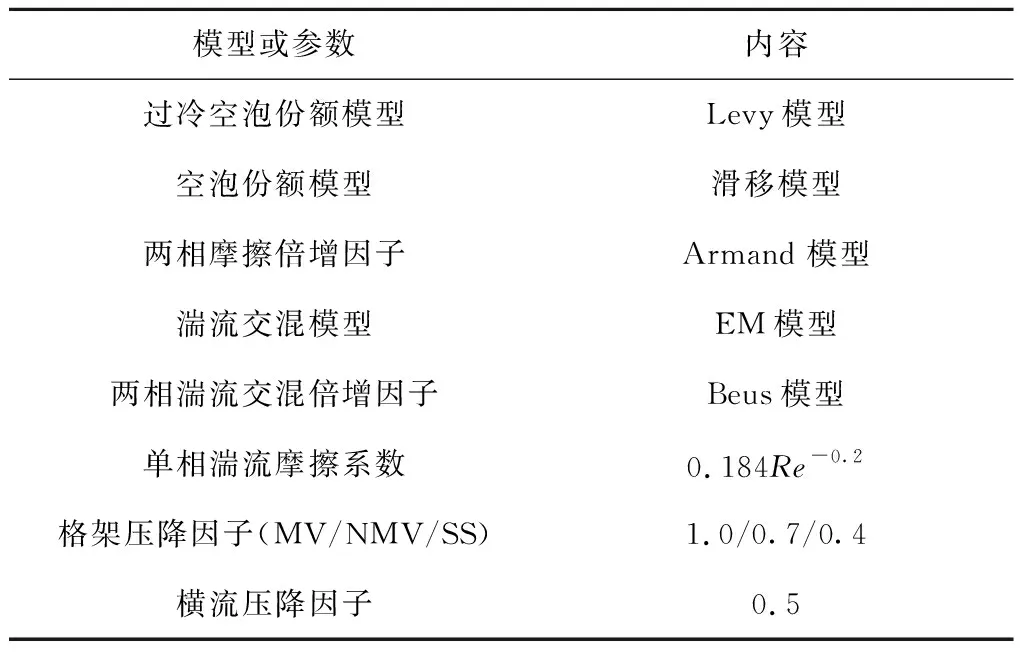
表3 PSBT基準題計算模型及參數選擇

模型參數使用基準值進行計算.如圖4所示，橫軸為空泡份額實驗值ve，縱軸為子通道程序空泡份額計算值vc，越接近黑色實線代表計算值與測量值越符合，上、下兩條虛線代表實驗測量不確定性2σ(=0.08).可知，較多的計算值位于實驗值的兩倍標準差(2σ)范圍之外，且整體預測值偏高，證明計算選用的模型過于保守，仍需要進一步改進.

在進行模型參數不確定性量化過程中，計算敏感性矩陣是重要步驟.在使用有限差分法求偏導數的過程中，步長的選擇并不是越小越好.因為步長太小可能會導致程序響應變化不明顯，也會受到數值不穩定性的影響，步長過大又會導致誤差過大.所以為了減小偏導數計算過程中的誤差，需要進行平滑處理[11].例如在求解滑速比和湍流交混系數對應的敏感性系數時，分別取步長為 ±0.01, ±0.03, ±0.1 來進行計算，對于每個樣本點可以得到6個偏導數，然后舍掉最大值和最小值，求平均值作為最終的偏導數.

3 計算結果分析

將壓力、入口溫度、質量流量、熱流密度當作已知分布參數，將滑速比和湍流交混系數作為待評估的模型參數，利用25組工況共50個實驗樣本點計算得到滑速比的均值和標準差分別為 0.440 5、0.259 9；湍流交混系數的均值和標準差分別為-0.103 4、0.048 8.可知，滑速比不確定性的標準差較大.根據最小熵增理論，滑速比的大小與壓力密切相關，而在進行模型參數的不確定性分析時所選用的工況壓力范圍為7.36～14.71 MPa，因而滑速比也存在較大的不確定性.為了驗證正態分布假設是否成立，使用卡方檢驗來驗證殘差是否滿足標準正態分布，將殘差劃分為10個區間，有：

(11)

則有95%的置信度認為參數服從正態分布.

在得到了輸入參數不確定性的具體分布之后，對另外5組工況進行不確定性的正向傳播.將得到的模型參數及邊界條件參數按照其分布進行93次抽樣，并通過子通道程序進行計算，將得到的最大值和最小值當作雙95%置信區間的上下界.圖5為4個中心子通道的空泡份額平均值計算值不確定帶對實驗值的包絡情況.可知，當空泡份額較高時，不確定帶對實驗值的包絡性非常好；當空泡份額較低時，不確定帶對實驗數據的包絡情況不夠理想，有部分未包絡，但不確定帶下界也非常接近實驗值.

利用所求出的統計均值對模型系數進行修正，圖6為基準模型修正前后4個中心子通道的空泡份額平均值計算結果對比.可知，樣本點模型參數經過均值修正后，計算結果與實驗值更接近，計算精度有了明顯改善.

4 結論

本文在假設輸入參數不確定性與輸出參數不確定性近似為線性關系的基礎上，將邊界條件壓力、入口溫度、質量流量、熱流密度當作已知分布輸入參數，對子通道程序COBRA-IV輸入模型參數中滑速比和湍流交混系數的不確定性進行評估；然后進行輸入參數不確定性的正向傳遞，得到了空泡份額的不確定帶，并利用求得的模型參數不確定性統計均值對模型進行修正，計算結果表明：

(1) 在所選取的空泡分布實驗工況范圍內，滑速比存在較大的不確定性，而湍流交混系數的變化范圍較小.

(2) 計算結果的不確定帶對實驗值的包絡情況較好，尤其是當空泡份額較高時.

(3) 利用統計均值對模型進行修正后，可以得到比原模型更接近實驗值的計算結果，對于輸入模型參數的不確定性評估結果可以作為計算模型改進的重要參考.