基于單神經元自適應的PWM整流器控制方法研究

胡春龍

(陜西國防工業職業技術學院，陜西 西安 710300)

0 引言

當前，電力電子功率器件層出不窮，尤其在電網電能變換領域應用極為廣泛，但由于負載的多樣性和控制的單一性，導致網側電流中產生了大量的諧波污染，電網利用率變低，因此綠色電源、電能質量成為了電網行業新的關注點。普通二極管或晶閘管搭建的整流橋，存在功率器件的開通和關斷過程并不是完全可控的，導致網側電流功率因數下降嚴重且無法實現電源能流的雙向轉換。三相脈寬調制(pulse width modulation，PWM)整流器由于在諧波抑制、功率因數改善和能流的雙向性方面具有眾多優勢，因此成為電能變換領域研究的熱點[1]。

PWM整流器運行的可靠性和穩定性主要取決于控制方法的先進性，目前應用最廣泛的控制方式為PI調節下的電壓、電流雙閉環控制，控制簡單但雙PI勢必會降低系統的響應速度，且直流側穩定性受負載影響較大，電能轉換的可靠性不高[2]。本文提出了一種單神經元自適應PID與傳統PI復合調節的新型控制策略，通過電壓外環的誤差值來對調節器進行動態選擇，利用神經元的自學習、自適應能力和PI對參數的快速整定特點，簡化了系統模型，降低了PWM整流器運行過程的尖峰電壓和電流，減少了網側電流諧波污染，提高了電流功率因數及系統運行的穩定性和可靠性。

1 電壓型全控PWM整流器數學模型

三相全控電壓型PWM整流器的拓撲結構如圖1所示。其中，左半部分為交流電網側，ua、ub、uc為三相對稱交流電源，ia、ib、ic為三相對稱電流，O為電源中性點，L為網側交流電感，R為線路等效電阻；右半部分為整流器直流輸出端，其中S1～S6為由功率開關管IGBT組成的整流橋6個橋臂，C為直流側濾波電容，Udc為整流直流電壓，RL為輸出負載，iL為負載電流[3]。

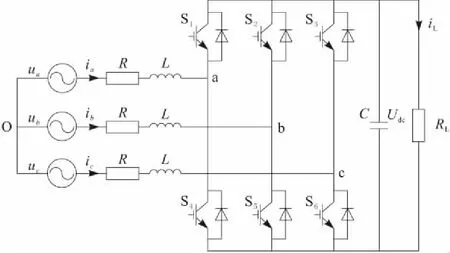
圖1 三相PWM整流橋主電路結構

整流橋臂功率開關管的每一種開關狀態分別對應一種輸出狀態，因此可通過對功率器件S1～S6的控制來實現對直流側電壓的控制。對于上下對稱的1組橋臂，規定狀態“1”為上橋臂導通，下橋臂斷開，可用Sk(k=1,2,3)=1分別表示三相橋臂的“1”狀態；規定狀態“0”為上橋臂斷開，下橋臂導通，可用Sk(k=1,2,3)=0分別表示三相橋臂的“0”狀態[4]。這樣，對于圖1中的電路結構，由基爾霍夫電壓定律可知，三相PWM整流器在a、b、c三相對稱靜止坐標系下的數學模型為

(1)

由基爾霍夫電流定律可知，直流側電流回路可以表示為

(2)

由式(1)和式(2)可知，靜止坐標系下的數學模型中包含微分方程，具有較大的非線性，為此根據等功率的原則，將靜止坐標系abc下的數學模型進行Park同步變換到dq坐標系下的數學模型為

(3)

id、ud、ed為無功分量；iq、uq、eq為有功分量；Sd、Sq分別為dq軸上的開關函數。

2 單神經元自適應PID調節系統

2.1 調節系統結構

三相PWM整流器運行的穩定性和可靠性很大程度上是由調節器設計的合理性決定的。本文在電壓外環控制中引入了一種單神經元自適應PID與普通PI相結合的新型調節器，其中，用于單神經元自適應PID調節過程的控制結構如圖2所示。

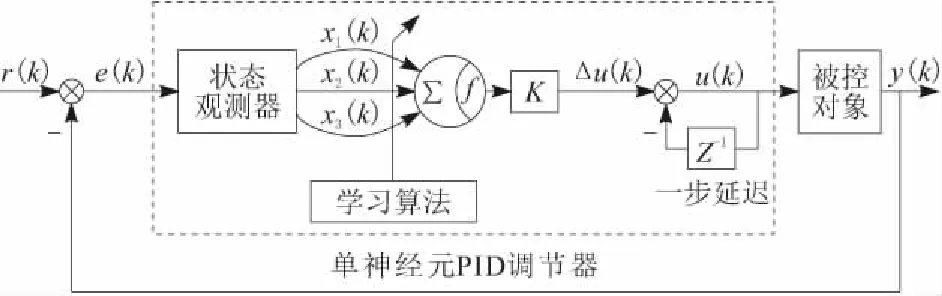
圖2 單神經元自適應PID調節系統

從圖2中可知，被控對象輸出y(k)與系統給定值r(k)進行作差比較，輸出誤差信號e(k)進入單神經元PID調節器中的狀態觀測器，實現微分運算[5]。在學習算法的干預下，由觀測器輸出3個狀態變量，為單神經元自學習、自整定提供控制參數，狀態變量x1(k)、x2(k)、x3(k)分別表示為

(4)

神經元在進行算法學習后，通過不斷搜索、調整對外部加權信號進行函數處理，最終輸出相應的控制信號為

(5)

K為神經元傳遞系數；ωi(k)為信號xi(k)對應的加權系數。

2.2 學習算法

給定信號與輸出信號之間誤差值的二次方是衡量神經元性能指標的一個重要依據，在加權系數ωi(k)的不斷調整下，性能指標函數自我修正并達到最小化，實現了PID自適應參數的優化控制[6]。單神經元性能指標函數一般選取為

(6)

要實現性能指標函數的最小化控制，在對加權系數ωi(k)進行調整、修正和搜索時，需沿著梯度減小的方向進行。調整過程中的加權誤差量一般為

(7)

ηi(i=1，2，3，4)為神經元在線學習速率。

在Hebb學習算法、規則的調整改進下，不斷地在線更新權值系數ωi(k)，經過優化后的新的學習算法為

(8)

ηP、ηI、ηD為學習速率，與PID的變化速率一一對應；ωi為歸一化權值。

3 電壓外環復合調節器設計

由前文可知，神經元通過不斷的加權、求和和映射來適應外界干擾信號，簡化了系統模型的同時有效抑制了外環出現的較大電壓誤差，解決了系統非線性、強耦合等問題。但神經元的多輸入單輸出特點，使得運算與處理過程較為復雜，具有一定的滯后性，無法滿足PWM整流器對快速性和電壓電流跟隨性的需求[7]。為此，設計了一種單神經元自適應PID與普通PI復合的控制器，如圖3所示。

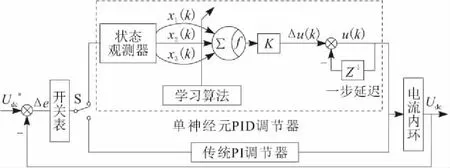
圖3 單神經元與PI復合調節器

通過開關表對電壓誤差進行判斷并輸出開關信號，實現單神經元自適應PID調節與傳統PI調節的快速切換。利用神經元的自我修正能力快速消除較大電壓誤差，利用傳統PI算法簡單、速率較快等特點對系統進行細調，綜合二者優點提高了控制的可靠性和穩定性。

4 電流內環前饋解耦調節器設計

為優化電流波形，減小諧波分量，提高電壓電流跟隨性，實現滿功率因數運行，需要對式(3)中的模型進行前饋解耦處理并經PI調節后得

(9)

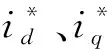
前饋解耦后的控制結構如圖4所示。

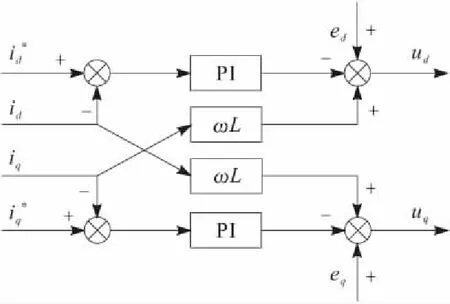
圖4 電流前饋解耦結構

將式(9)代入式(3)中可以得到電流完全解耦后的線性模型為

(10)

在電流無功分量為0的情況下，電流內環只需對解耦后的有功分量進行控制[8]。

下面對電流內環PI調節器進行設計，因電流內環在解耦后滿足對稱性，故以iq為例按照典型I型系統設計電流調節器，在忽略ed干擾的情況下，電流內環可以設計成如圖5所示結構。

圖5 電流內環系統結構

由圖5可以看出，在電流內環調節過程中，需要將內環結構傳遞函數的極點抵消PI調節器中的零點即可，即τi=L/R，這樣通過優化后的電流內環傳遞函數可以表示為

(11)

KiP為比例參數；KPWM為PWM整流器等效增益；Ts為采樣周期。

5 三相PWM整流器仿真模型

在MATLAB/Simulink仿真環境下，對三相電壓型PWM整流器建立了仿真模型，實現了單神經元自適應PID與普通PI復合調節下的雙閉環控制。仿真模型如圖6所示。

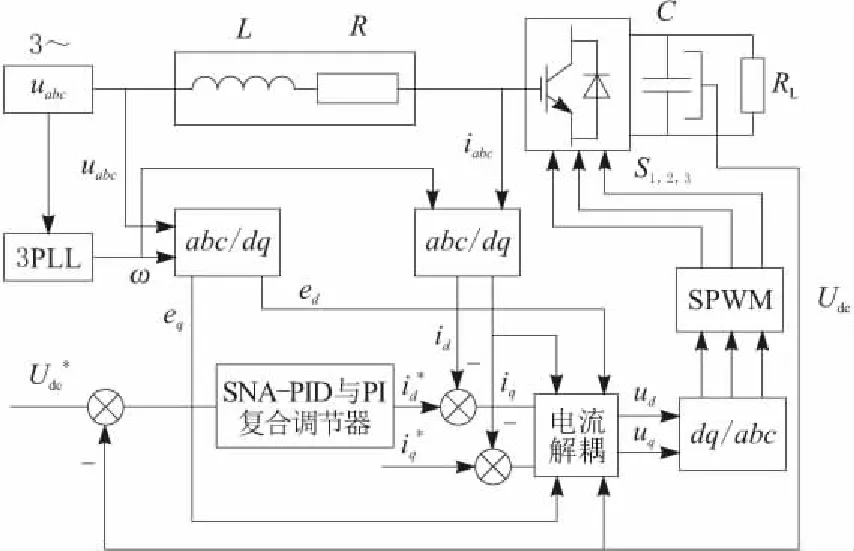
圖6 雙閉環控制系統

系統模型搭建完成后，設定相應仿真條件，PWM整流器的仿真參數設置如表1所示。

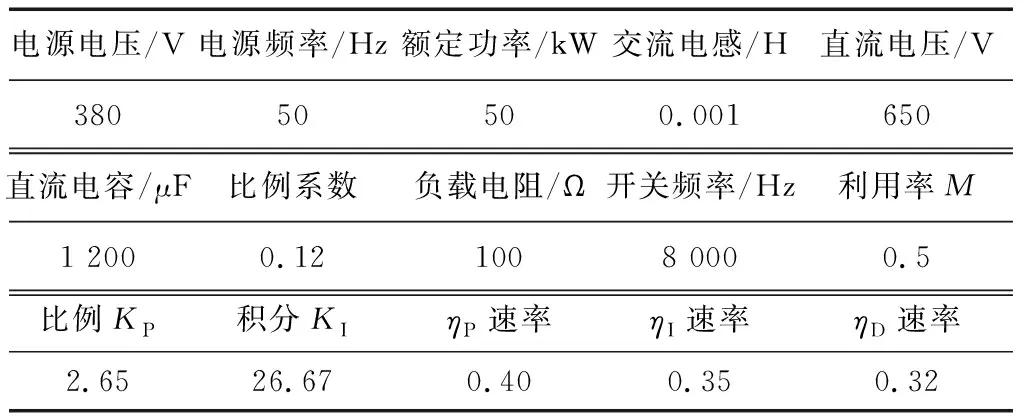
表1 仿真參數

6 仿真結果與分析

圖7為A相輸出電流和電源A相電壓對比曲線，從圖7中可以看出輸出電流能夠很好的跟蹤電源電壓，在0.01 s時與電源電壓保持同頻率同相位，具有較好的跟隨性和快速性。

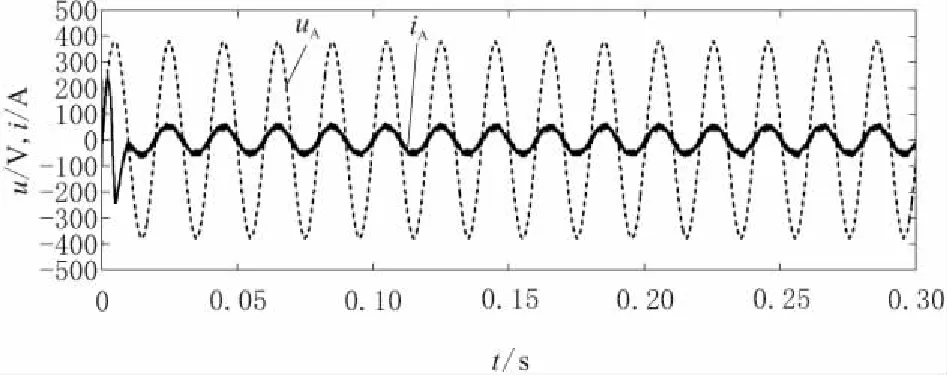
圖7 相電流與交流相電壓曲線對比

為了體現電壓外環中采用單神經元自適應PID與傳統PI復合調節器的優越性，仿真中將其與外環僅采用傳統PI調節器下的輸出電壓進行了對比，起動階段給定電壓為650 V，系統輸出如圖8所示。

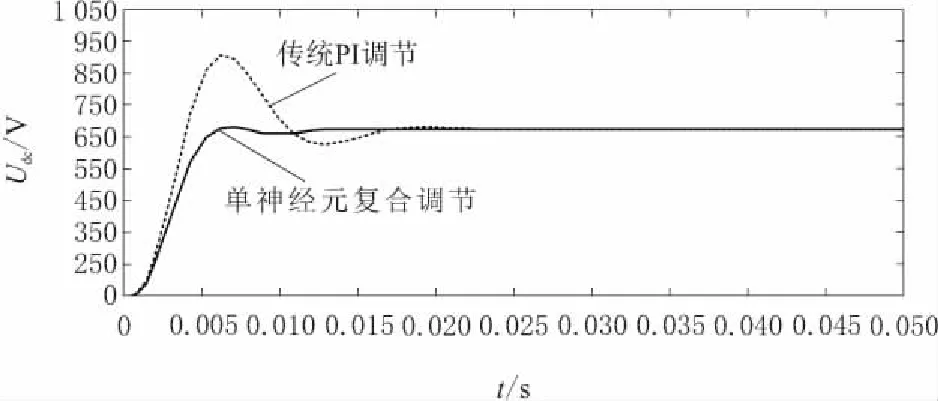
圖8 單神經元復合調節與傳統PI調節下的電壓曲線

從圖8中可以看出，采用單神經元復合控制調節時間約為0.012 5 s，輸出在0.015 s時達到給定值;采用傳統PI控制調節時間約為0.018 s，輸出在0.023 s時達到給定值，系統響應低于復合調節器且具有較大的電壓超調量，約為44.6%。

為了對比2種調節器下系統輸出的可靠性和動態響應，將輸入給定進行突變，在0.036 s時,將給定直流電壓跳變到750 V，0.09 s時給定電壓又恢復到650 V,如圖9和圖10所示為2種調節器輸出曲線對比。

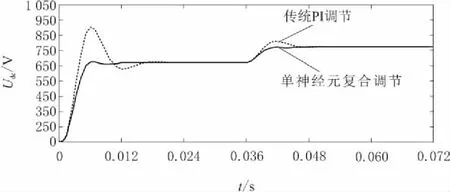
圖9 給定突變到750 V時的輸出

從圖9和圖10可以看出，無論是在起動階段還是給定發生突變階段， 單神經元復合調節器下的電壓超調和調節時間都明顯優于傳統PI單獨作用時，系統在單神經元復合調節器的作用下具有良好的可靠性和動、靜態性能。

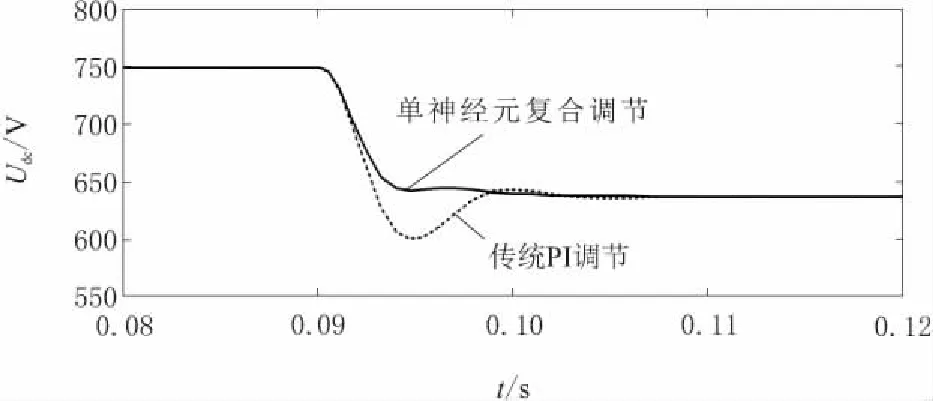
圖10 給定恢復到650 V時的輸出

7 結束語

本文以三相電壓型PWM整流器為研究對象，在分析了整流器數學模型及電壓電流雙閉環控制的基礎上，設計了一種單神經元自適應PID與傳統PI復合調節器代替電壓外環PI控制，結合了神經元和PI的優點，有效解決了雙PI控制的滯后性和穩定性問題，同時在電流內環引入前饋解耦，實現了對有功電流和無功電流的獨立控制。最后通過仿真實驗對雙閉環PI調節和單神經元自適應PID復合調節進行了仿真分析，通過對仿真結果的比較，發現單神經元自適應PID復合調節器要比雙PI調節器更高的魯棒性，在給定發生突變時，動態響應更迅速，可靠性更高。