三面骰子的動力學分析和幾何特性
范祥彬,盧奕合,劉逍娜,王鐵成
(山西大學 物理電子工程學院,山西 太原 030006)
2022年CUPT第7題:硬幣落地時側面站立的情況十分罕見.為了使圓柱形骰子落下時立在側面、正面與反面概率相同,應該具有怎樣的物理性質和幾何特征?
目前已經有研究者對三面骰子的問題展開過詳細的描述[1],但是仍然存在一些細節沒有得到解答.例如,在投擲三面骰子時,如果給予它水平方向的速度,側面出現的概率會發生什么變化? 三面骰子反復彈跳是否會有不同的結果?基于以上問題,本文進行了相關研究和討論.
首先,把硬幣定義為圓柱體,當它充分翻轉落地時,雖然側面出現的概率極小,但卻不能忽略其可能性.硬幣除了有1個平移自由度外,還有2個旋狀自由度,但是在實際情況下,由于硬幣的對稱性(側面高度趨于零),平移自由度作用并不明顯,因此可以認為理想硬幣落在正面或者反面的概率近似為1/2,但是一旦改變其側面的厚度,立在側面的概率就會改變,正面或者反面的概率將不再是1/2.
對于硬幣、正方體骰子和陀螺骰子而言,立在不同面的概率可以通過物體的對稱性來預測.但當物體不再具有精確的對稱性時,立在不同面的概率就不可能只受幾何特征的影響,還需要考慮彈跳的影響.
1 三面骰子的定義
三面骰子的立體圖及截面圖如圖1所示,設圓柱半徑R與高度h的比為
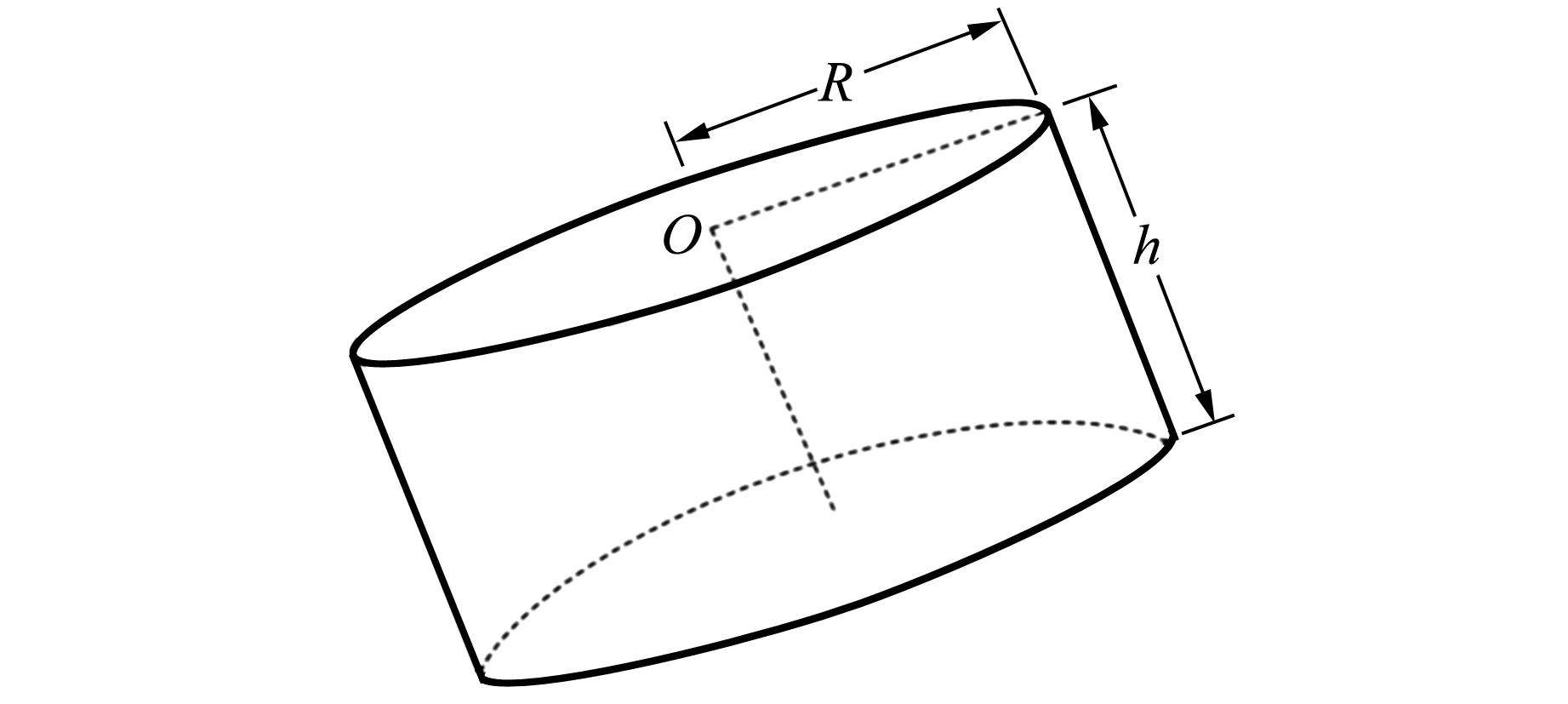
(a)立體圖
(1)
則內角為
β=2arctan(2η),
(2)
(3)
2 骰子的投擲方式
研究者們大都假設三面骰子豎直下落,而不具有水平方向的速度,下面給出簡單的理論解釋.
假設在t=t1和t=t2時刻,系統的位置由2組坐標q(1)和q(2)確定,則系統在這2個位置之間的運動積分
(4)

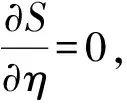
(5)
故
(6)
函數L為給定系統的拉格朗日函數或拉格朗日量,積分S為作用量.
當僅考慮三面骰子落地時的狀態(落地前的運動行為不考慮),假設骰子在地面沿直線滾動.現以三面骰子向前滾動時的2種極端的運動方式為例,即側面滾動和正反面輪流翻滾(圖2).利用式(1)求出這2種運動方式的η值,其他運動方式的η值介于這兩者之間.

(a)側面滾動 (b)正反面輪流翻滾
2.1 側面滾動

(7)
(8)
拉格朗日量
(9)
根據拉格朗日方程,則有
(10)
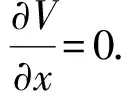
(11)
積分可得
x=C1t+C2.
(12)
2.2 正反面輪流翻滾
如圖2(b)所示,骰子勢能V不再是常量,并其轉動慣量為
(13)
故動能可表示為
(14)
拉格朗日量為
(15)
根據拉格朗日方程可得:
(16)
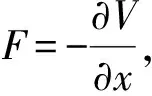
(17)

(18)
對比圖2(a)和圖2(b),可以看到在圖2(b)情況下,骰子會受到額外的耗散力影響,因此圖2(a)消耗能量較少,圖2(b)消耗能量較多,其他運動狀態則介于二者之間.由于圓形物體滾動時,其重心高度相對于地面接觸點不變,滾動時不需要克服重力做功,處于能量最低態,是最穩定的運動方式.因此骰子總是趨向于側面著地.
在現實情況中,首先骰子會受到地面的影響,使得骰子滾動時的軌跡為曲線,但曲線軌跡并不會影響結論;其次,滾動摩擦力比最大靜摩擦力小得多,側面滾動主要受到滾動摩擦,正反面翻滾主要受到最大靜摩擦,即前者相比后者更能保證運動最大量,可以很大程度上減小克服摩擦力做功.因此,即使考慮摩擦影響,骰子也是趨向側面滾動狀態.所以可得出以下結論:三面骰子如果具有水平方向的初速度,骰子總是趨向于側面著地向前滾動.性質會影響骰子立地概率的公平性,從而導致實驗結果與實際情況不符.
那么,是否可以得出具有一定厚度的三面骰子都是趨向于側面著地的結論呢?對此,對不同尺寸的三面骰子的著地情況進行統計,結果如表1所示.
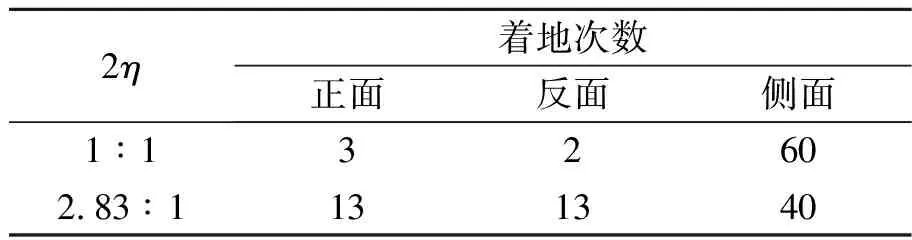
表1 不同尺寸的三面骰子著地的情況
實驗采用的骰子直徑2R=2.500 cm,h=0.833 cm,如若不給初速度,正常投擲,大都會認為骰子正反面著地的可能性大,然而表1卻是側面落地的次數多,表明骰子向前投擲會增加側面著地的概率,與理論猜想相同.
同樣利用硬幣進行翻滾實驗時,大多數情況下也都是側面向前滾動的情況,但由于硬幣的側面尺度很小,立地條件不足,容易受到外界擾動的影響,所以不論怎么拋擲都不會影響公平性.
如果地面光滑,采用向前拋擲的方法,硬幣便不會受到外界擾動,將保持自身的慣性,從而有可能出現側面立地的情況.因此,在投擲圓柱形骰子時,盡量保持骰子在水平方向無初速度.
3 三面骰子實驗設計
圖3所示骰子是以ABS材質為原材料的實心圓棒,利用游標卡尺測量長度,通過手工鋸和銼刀切割磨皮,雖以上制作方法存在較大誤差(手工切割所帶來的正反兩面的不對稱),但由于目前只是驗證模型,即只需證明側面出現的概率接近1/3,因此可以忽略誤差帶來的影響.骰子直徑固定2.500 cm,制作不同高度的骰子,實驗時1次性投擲5個相同高度的骰子,多個數據點可以避免單一骰子帶來的固有偏差[3].

圖3 手工骰子
第2章已證明三面骰子水平方向不應具有初速度,為了避免這種情況,設計了如圖4所示的投擲裝置.
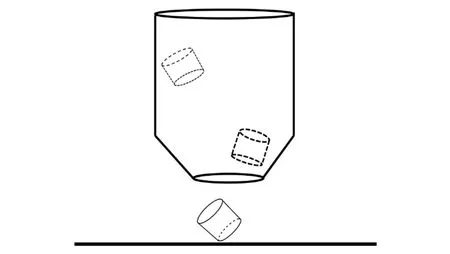
圖4 投擲裝置示意圖
將骰子從寬口丟下,讓骰子充分旋轉,在骰子接近窄口時,由于路口變窄,骰子劇烈震蕩,骰子的轉動動能部分損失,并轉化為豎直向下的動能,這樣就滿足了第2章中論述的限制條件.改變投擲裝置的高度,可改變骰子的彈跳情況.投擲裝置采用5 L礦泉水桶裁去桶底部分制作.
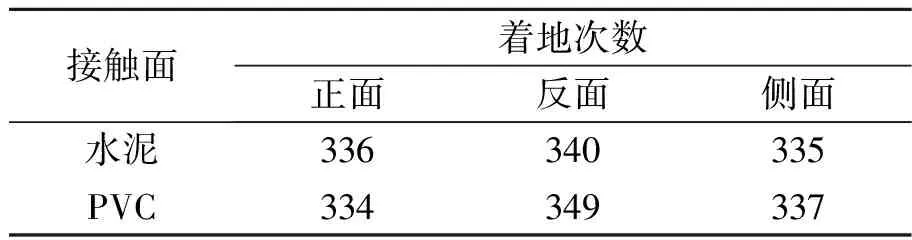
當三面骰子豎直落地時,由于邊緣落地帶來的反彈,能量在豎直方向可能無法抵消,從而讓骰子具有水平方向的動能(在同一豎直線反復彈跳的結果不太可能出現),那么當出現該情況時,需要舍棄該結果并重新投擲.此外,設計骰子分別在水泥和PVC材質的接觸面上著地.
4 三面骰子模型
在完全不考慮反彈的情況下提出了3種三面骰子的模型,出發角度各不相同,得出的結果也有差異.為了驗證前文內容,設置了3種實驗環境:在無初速度時水泥面和PVC面著地,以及有初速度時,骰子在水泥面著地的情況.
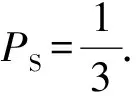
4.1 圓柱體表面積模型
通過借鑒標準正方體骰子出現等概率性的特性,猜想表面積可能是影響因素之一,于是得出:
(19)
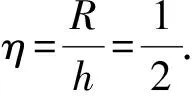

表2 圓柱體表面積模型骰子著地情況
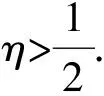
4.2 立體角模型

(a)立體圖
設球冠的表面積為A,利用微元法求解.在球冠上取細小的圓環,半徑為r,弧長為dl=Rdθ,于是面積為
dA=2πrdl=2πrRdθ,
(20)
(21)
因r=Rcosθ,則
(22)
(23)
由立體角公式,有
(24)
為使其平均,應該使得立體角為
(25)
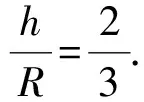
(26)
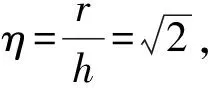

表3 立體角模型骰子下落情況
由表3中數據得:水泥接觸面時骰子的正面概率PA=0.443,反面概率PB=0.383,側面概率PS=0.174;PVC接觸面時骰子的正面概率PA=0.427,反面概率PB=0.363,側面概率PS=0.210.很明顯,側面概率與理想值0.333有較大偏差.故馮諾依曼假設僅在數學模型上合理,但與實驗結果不符.
4.3 重心模型
圖6為三面骰子落地時與接觸面接觸時的一種狀態,重心線的偏向決定了三面骰子倒地的結果[5],θ為重心線與x軸的夾角,OH為重心線,決定骰子的偏向.
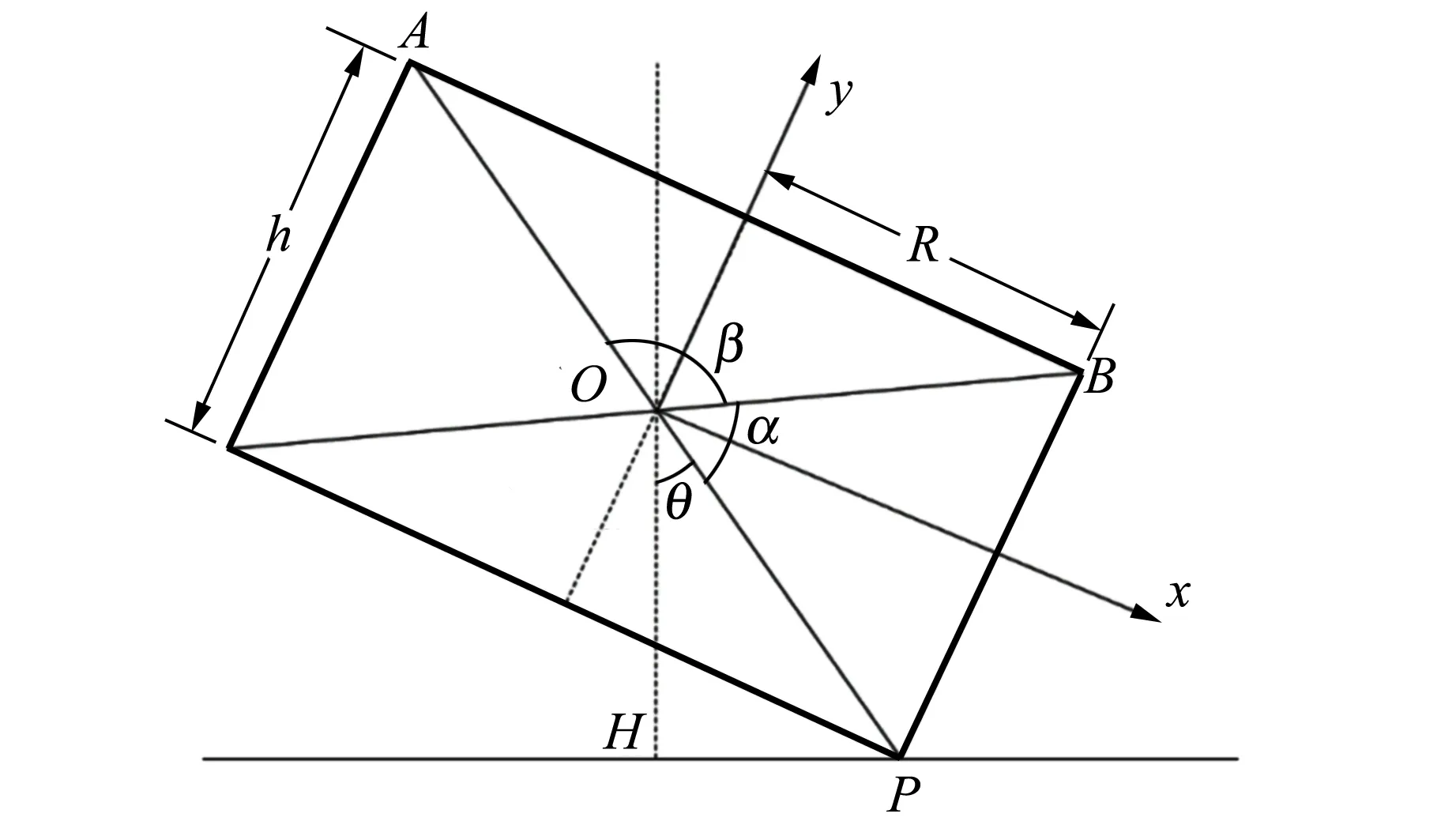
圖6 圓柱骰子截面圖
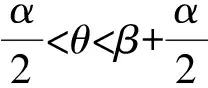

表4 重心模型下骰子下落情況
由表4中數據可得:接觸面為水泥且無初速的條件下,骰子正面概率PA=0.335,反面概率PB=0.322,側面概率PS=0.343,側面相對偏差Er=3.0%;接觸面為PVC且無初速的條件下骰子正面概率PA=0.320,反面概率PB=0.351,側面概率PS=0.328,側面相對偏差Er=1.5%.數據與理論吻合較好.
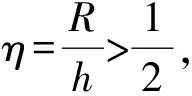
5 彈跳模型
上文僅考慮了三面骰子落地瞬間便損失全部動能的情況,現以簡單彈跳情況為例進行分析.假設每次落地損失一部分動能,即三面骰子經過多次反復彈跳才會停止,并且每次落地彈跳之后會經過充分旋轉,再次落地時方向依舊隨機.假設初始時,三面骰子具有能量E,第一次與地面碰撞后能量為γE,第n次碰撞后能量為γnE(n=1,2,3…),其中γ<1為衰減系數[6].
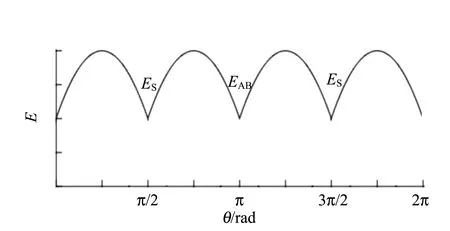
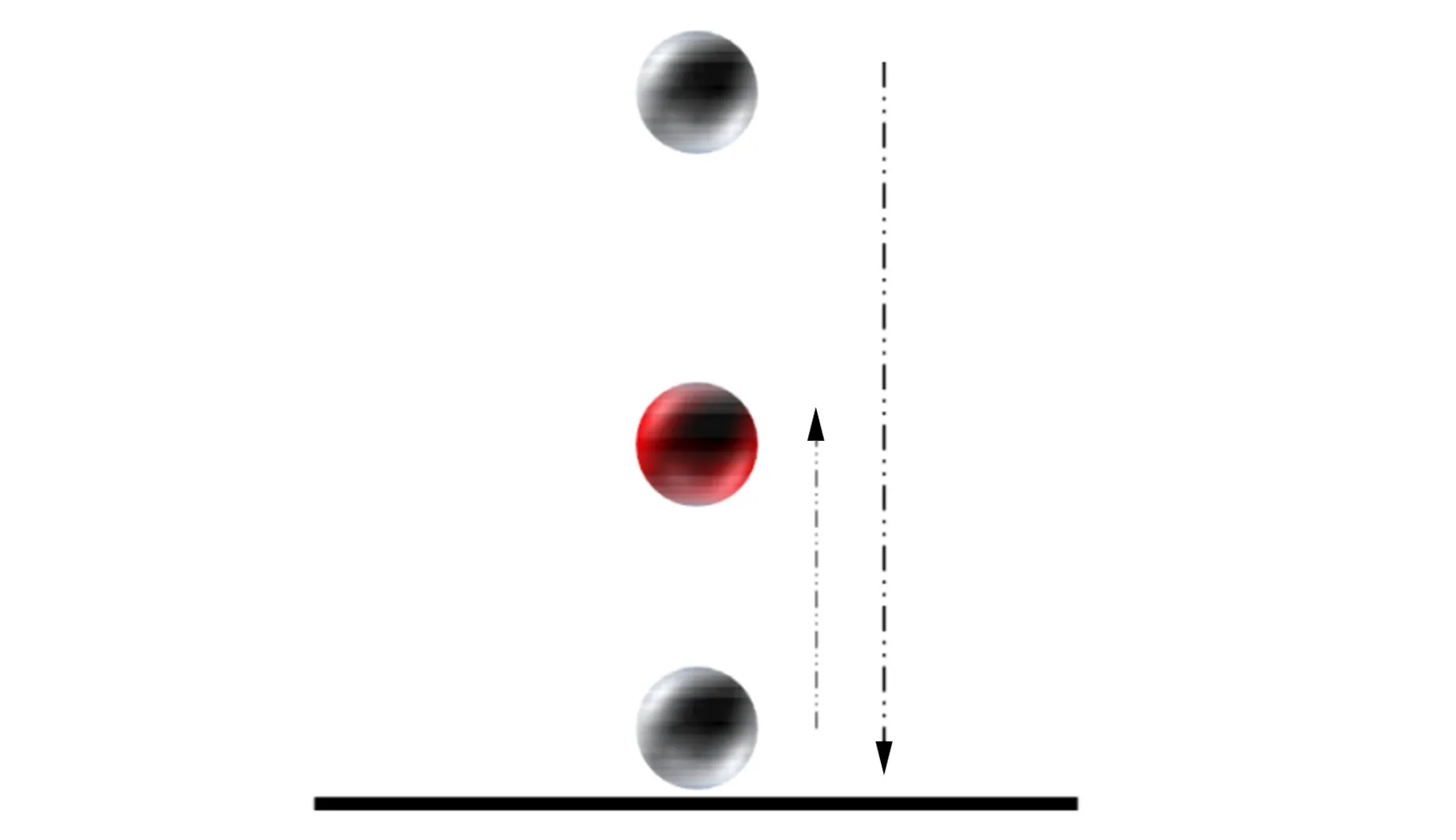
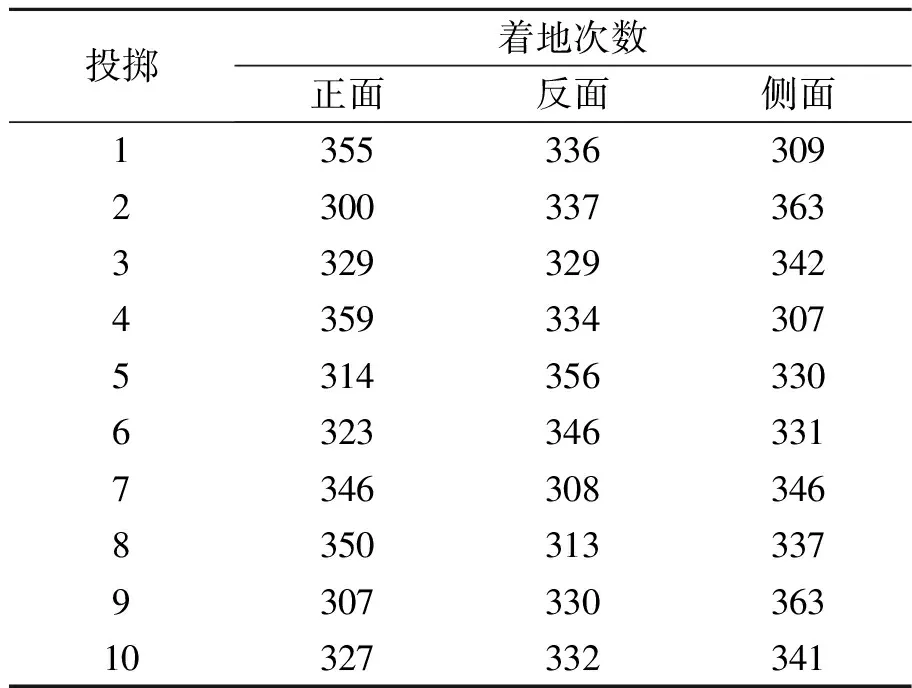
定義2個能量值EAB和ES,它們分別表示底面和側面的能量勢阱,如圖7所示.假設底面的勢阱高,即ES>EAB(若ES 圖7 ES>EAB情況下對應的能量勢阱圖 此時落在2個山谷的概率正比于兩側山峰的間距,則會出現如下情況: 1)假設經過n次彈跳,能量為EAB<γnE,γn+1E (27) 該假設還可以表述為:假設前m次碰撞,其能量為γmE>ES,而EAB<γm+1E 2)假設經過n次碰撞后能量為γnE (28) (29) (30) (31) 現考慮式(28),則 (32) (33) 該結果與式(30)和式(31)相同. 當ES=EAB時,對應如圖8所示的能量勢阱.骰子經過n次彈跳后,能量為γnE 圖8 ES=EAB情況下對應的能量勢阱圖 (34) 此條件下得到的結果,與前面結果相同,但此種情況很特殊,等式成立的條件比不等式成立更加苛刻,因此不易實現. 在本節中,得出結論有:三面骰子不允許多次彈跳,否則實驗結果會出現很大偏差.所以實驗過程中要求三面骰子落地后,動能必須立刻損失或彈跳1次后減為零,否則將不會出現等概率事件. 在構造彈跳模型時,沒有給出E和r的數值,因此做了如下假設: a.每次碰撞后的能量衰減參量不變,并且各個接觸點的衰減參量都相同; b.每次彈跳落地前都經過充分旋轉,落地后再次隨機; c.E和γ不同取值不會導致其他影響; d.從始至終只有骰子的豎直方向有動能,且反彈不會帶來方向的偏移. 上面4個假設的約束性較強,使得彈跳模型局限性較大.根據熱力學模型的建立過程可知,模型的限制越多,模型與實際情況就越可能畸變.三面骰子不像正方形骰子、異體形骰子,每個面都有精準的對稱性,因此需做出一些條件假設求解三面骰子模型. 根據本節內容,n=0的情況與4.3節相同,現給出n=1,2時的實驗數據,如表5~6所示. 表5 n=1,η=時骰子的下落情況 由表5可知:當n=1,接觸面為水泥時,骰子的正面概率PA=0.330,反面概率PB=0.349,側面概率PS=0.321,側面相對偏差Er=3.6%. 猜想n=0,1情況下,實驗結果相差不大的原因只是由于碰撞1次帶來的效果不特別明顯,為了滿足骰子只碰撞1次,需要調節高度來實現,在實驗中,這種高度不足以產生特別明顯的誤差.圓柱形骰子是不完美對稱的,因此碰撞之后會使骰子的運動方向改變.因此骰子具有水平方向的初速度,也會導致側面的概率發生變化. 由圖9可以看出,不完美對稱的物體反彈以后,會偏離原來的運動方向,由能量守恒可知,骰子具有了水平方向的速度,根據第2章內容,骰子側面著地的概率將會增加. (a)高度對稱球的反彈 通過簡單的測試發現,骰子豎直落下,發生彈跳,側面著地的次數會大大增加(表7),這樣的結果與第2節的內容相符.所以給出的結論是:實驗過程中,保持n=0才最為合理. 表7 發生彈跳后的骰子下落情況 表6 n=2,η=0.391 2時骰子下落情況 綜上所述幾何和反彈模型共同說明:圓柱形骰子須無反彈、無水平初速度的投擲才能保證其等概率著地. 圖10 3D打印骰子 表8 標準骰子的下落情況 接觸面為水泥面時,骰子正面概率PA=0.332,反面概率PB=0.336,側面概率PS=0.331,側面相對偏差Er=0.6%. 接觸面為PVC面時,骰子正面概率PA=0.327,反面概率PB=0.342,側面概率PS=0.330,側面相對偏差Er=0.9%. 利用Pycharm軟件進行模擬如圖11所示,模擬投擲次數為1 000次,做了10次模擬的數據如表9所示. 表9 Pycharm軟件模擬投擲情況 圖11 Pycharm軟件模擬 從實驗數據上可以看出,實驗結果與理論分析較吻合,如果需要更接近333的數據,可以通過調節滾動摩擦力來實現.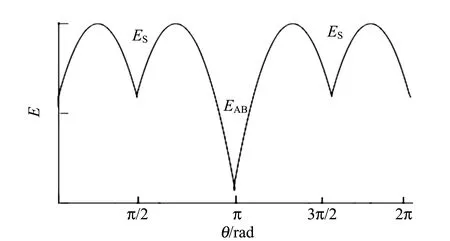

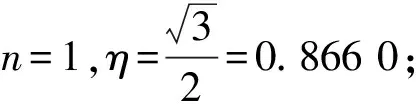

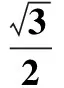
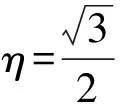

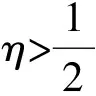

6 標準骰子實驗


7 結 論


