矩形渦流發生器結構參數對圓形換熱管傳熱特性的影響

朱世權， 胡宗要， 程傳曉， 李龍江， 彭義森， 陳志華， 鄭純， 金聽祥*

(1.鄭州輕工業大學能源與動力工程學院， 鄭州 450002； 2.南京理工大學瞬態物理國家重點實驗室， 南京 210094)

在節能減排的背景下，提高能源利用效率無疑是實現綠色可持續發展的重要措施，而強化傳熱技術是提高換熱器效率，提高能源利用效率的有效途徑之一[1-2]。強化傳熱技術可分為：主動式、被動式和復合式[3]，主動強化傳熱技術需要外部能量輸入，包括表面振動、脈動流和施加電磁場等[4]。被動強化傳熱技術不需要外部能量輸入，通常包括異型管、粗糙表面和插入物等[5]。被動強化傳熱技術具有成本低、制造簡單等特點，在工業中的應用廣泛[6]。

渦流發生器是換熱器最常用的被動強化傳熱技術之一，縱向渦強化傳熱技術一直是強化換熱研究的重點[7]。縱向渦流發生器是渦旋平行于主流方向的渦流發生器。研究表明，縱向渦流發生器在增強傳熱性能方面具有顯著優勢，因為縱向渦流發生器誘導流體擾動產生縱向渦，干擾管芯和壁面流體的流動，并繼續向下游延伸[8]。近年來，在換熱通道內布置不同形狀的渦流發生器得到了廣泛關注。Samadifar等[9]在三角形換熱通道內比較了矩形渦流發生器、斜切矩形渦流發生器、角矩形渦流發生器、Y形渦發生器和波狀渦流發生器的傳熱性能，結果表明簡單矩形渦發生器比其他形狀的渦流發生器更能提高翅片換熱器的換熱性能。Uddip等[10]在矩形換熱通道內研究了矩形渦流發生器表面紋理對傳熱和流動的影響，結果顯示，在渦流發生器的前導面上設置多個凹型廓線有利于強化傳熱。Naik等[11]在矩形換熱通道內研究了彎曲矩形渦發生器的流動和傳熱特性，發現渦流發生器前緣上部、尾緣上部和頂緣產生的縱向渦對邊界層的擾動和尾跡區流體混合的改善起著重要作用。Song等[12]研究了在層流條件下平板換熱器通道內布置凹、凸曲面三角形渦流發生器的換熱性能，結果表明，凹型彎曲三角形渦流發生器更有利于強化傳熱。Sun等[13]和Zhang等[14]對圓形換熱管內空氣的強化傳熱問題進行了研究，矩形渦流發生器在管道內產生了縱向渦，增強了管內空氣的混合，起到了強化傳熱的作用。Promvonge等[15]研究了在圓形換熱管中心插入V型排布的矩形和三角形渦流發生器的傳熱性能，結果表明兩種渦流發生器的強化傳熱效果均優于光滑管道，V型排布的矩形渦流發生器整體強化傳熱效果略優于三角形。

綜上所述，使用渦流發生器強化傳熱的研究有很多，大多數研究是在管道壁面上安裝不同形狀的渦流發生器，或是在管道中心插入渦流發生器，而圓形換熱管內矩形渦流發生器長高比和安裝角對傳熱性能的影響還有待進一步研究。為此，選擇在圓形換熱管壁面安裝矩形渦流發生器的方式，對換熱管內水的加熱過程進行強化，分析換熱管內的傳熱和流動特性，研究矩形渦流發生器長高比L/H和攻角β對傳熱和流動特性的影響。

1 數值模擬

1.1 物理模型

內置矩形渦流發生器的圓形換熱管幾何模型如圖1所示，圓形換熱管內徑D= 0.047 m，測試段長度為1 m。換熱管周向布置4個傾斜的矩形渦流發生器，相鄰兩個渦流發生器呈V型排布，渦流發生器前緣距離測試段入口0.2 m。渦流發生器高度H和寬度分別為0.0 047 m和0.001 m，渦流發生器長高比L/H= 0.5～3，攻角β為10°～ 50°。為了保證數值計算時測試段處于充分發展段，出口不出現回流現象，將計算域向上游和下游分別延長0.5 m和0.3 m。

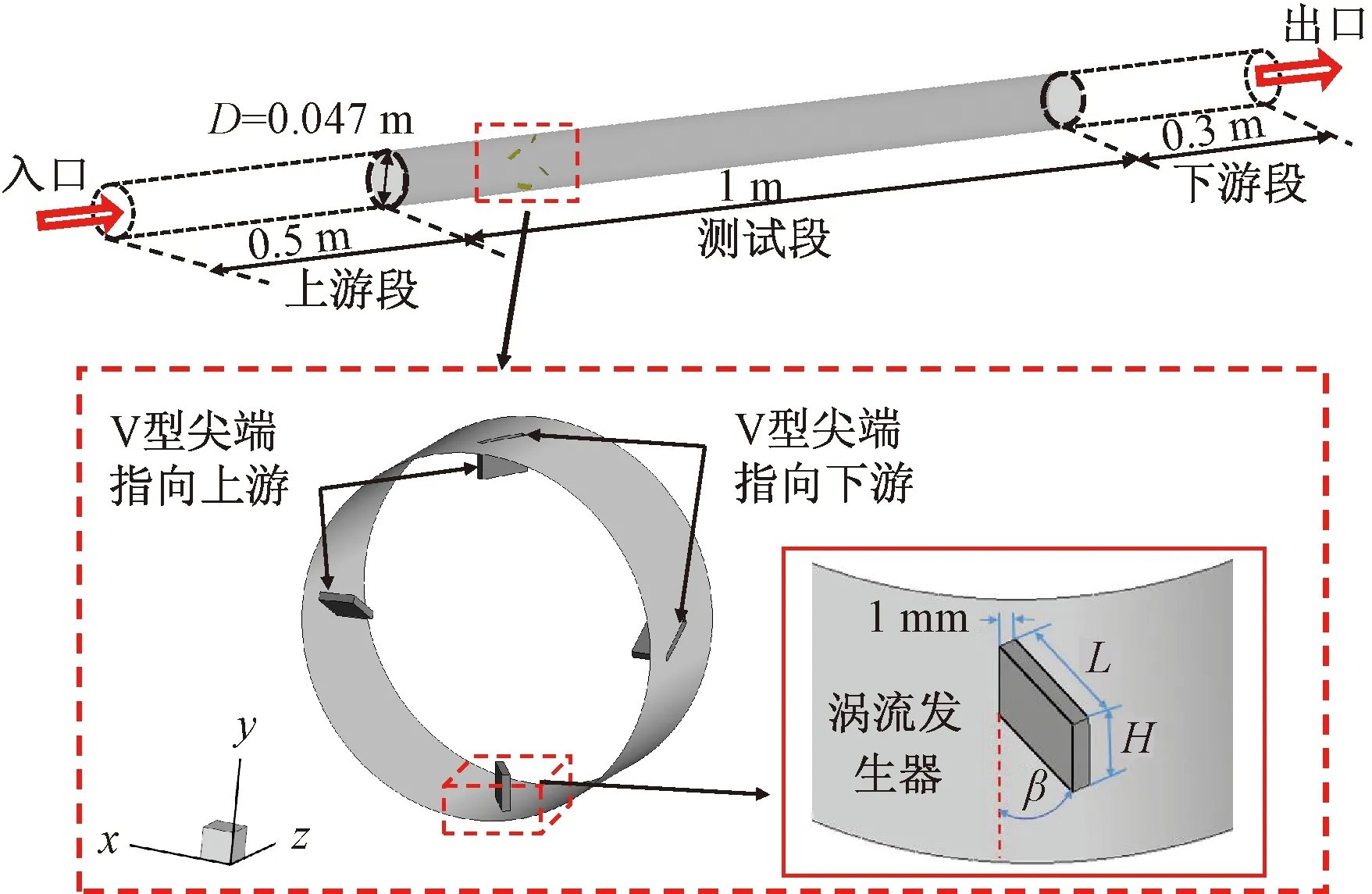
圖1 幾何模型Fig.1 Geometric model

1.2 數學模型

假設流動為穩定的、三維的和不可壓縮的。利用FLUENT軟件對其控制方程進行求解，采用SST(shear-stress transport)k-ω湍流模型(k為湍動能，ω為耗散率)。計算區域滿足連續性方程、動量方程、能量方程以及k和ω方程，具體表達式如下。

連續性方程為

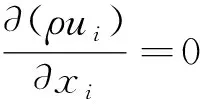
(1)

動量方程為

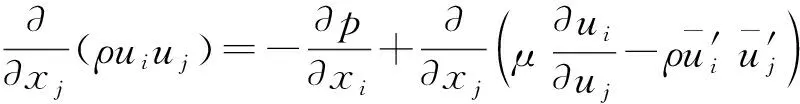
(2)

能量方程為

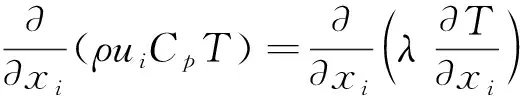
(3)

k和ω方程分別為

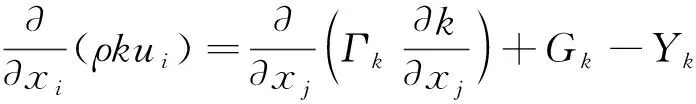
(4)

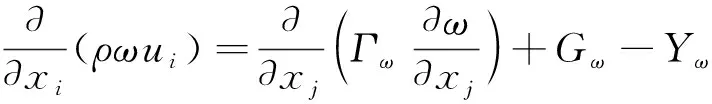
(5)

1.3 邊界條件

計算域采用速度入口和壓力出口，入口速度為0.2～0.6 m/s，速度方向垂直入口面，入口溫度恒為293 K，所有固體壁面均定義為無滑移邊界條件，延長段壁面為絕熱邊界條件。本研究為加熱管內流體，測試段壁面為等熱流邊界條件，熱流恒為30 kW/m2，假設渦流發生器表面的熱流密度為0。工作介質水的物理性質：普朗特數Pr=7.02,ρ=998.2 kg/m3,Cp=4 183 J/(kg·K)熱導率k=0.6 W/(m·K)，動力黏度η=0.001 003 Pa·s。

1.4 模型驗證

為了驗證數值計算方法的正確性，首先對光滑管道內的流動和傳熱過程進行數值模擬，并將計算結果和經驗關聯式進行比較，結果如圖2所示。可以看出，與Gnielinski關聯式[式(6)]和Dittus-Boelter關聯式[式(7)]相比，努塞爾數Nu最大誤差分別為7.04%和7.67%；與Filonenko關聯式[式(8)]和Blasius關聯式[式(9)]相比摩擦因子f最大誤差分別為6.93% 和6.47%。說明所使用的數值模擬方法是可行的。

(1)Gnielinski公式為

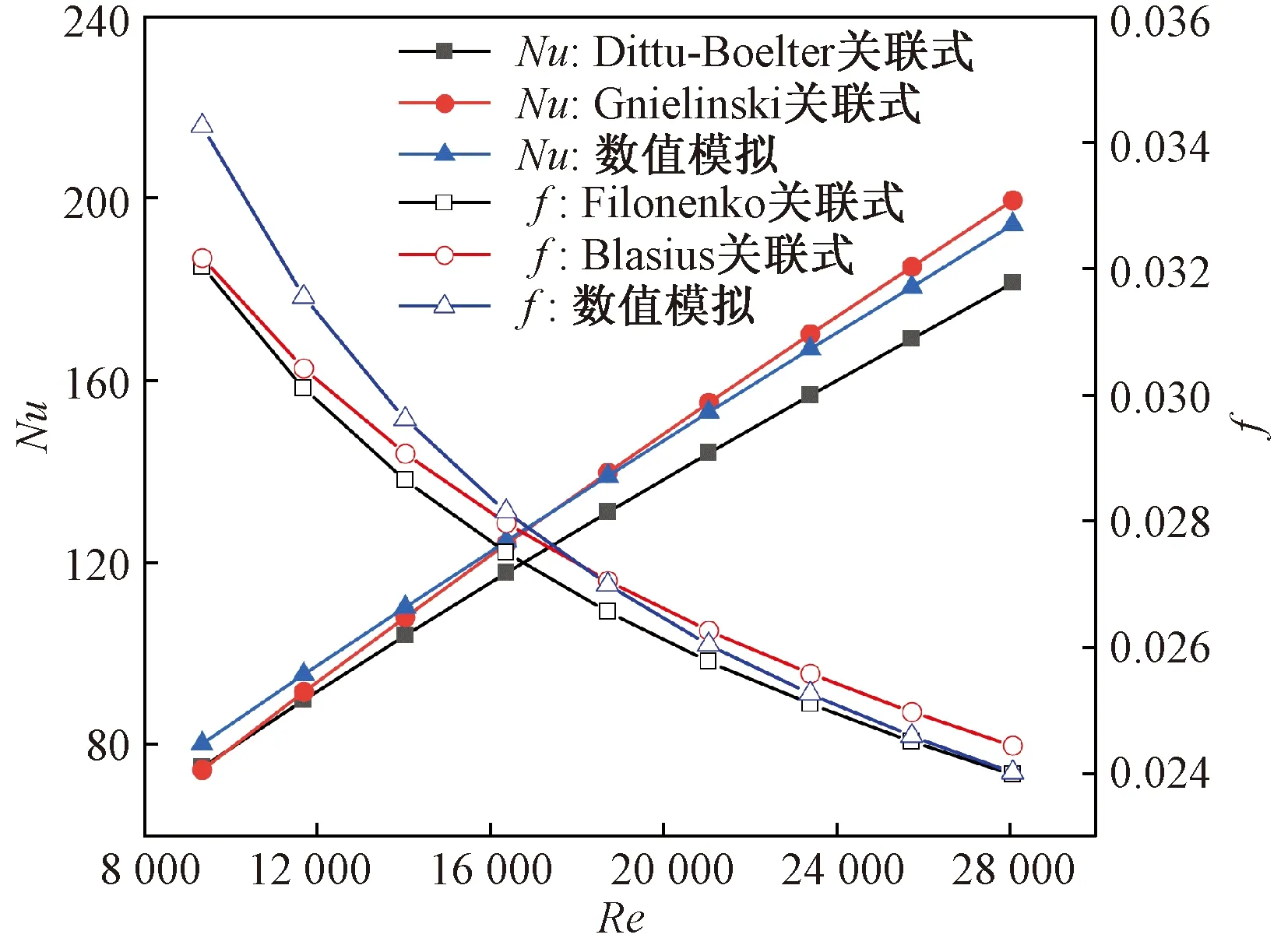
圖2 Nu和f 與關聯式的對比Fig.2 Comparison of Nu and f with correlation

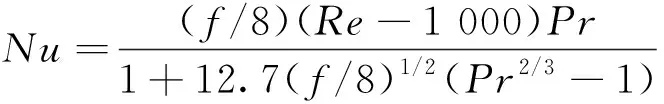
(6)

式(6)中：Re為雷諾數。

(2)Dittus-Boelter公式為

Nu=0.023Re0.8Pr0.4

(7)

(3)Filonenko公式為

f=(1.82lgRe-1.64)-2

(8)

(4)Blasius公式為

f=0.316Re-0.25

(9)

2 結果與分析

2.1 傳熱和流動特性分析

圖3對比了渦流發生器攻角β為10°和30°兩種工況下，介質流過渦流發生器的跡線。隨著攻角增大，渦流發生器下游產生較大的紊亂尾跡，尾跡線呈螺旋狀發展，與管道軸線相比略有偏移。攻角β為10°時，尾跡線發生少量偏移，出現了不太明顯的螺旋形流跡；攻角β為30°時，渦流發生器下游的尾跡線偏移了很多，形成了非常明顯的螺旋形流跡。

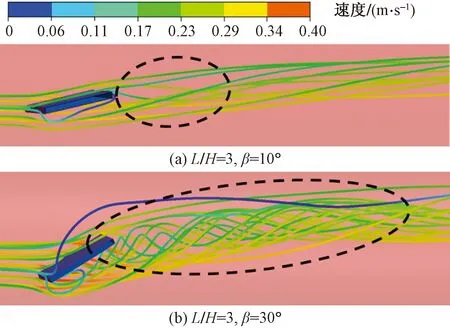
圖3 渦流發生器附近流體跡線(L/H=3, Re=14 000)Fig.3 Pathlines released from near the vortex generator(L/H=3, Re=14 000)

圖4為不同工況下換熱管壁面Nu分布云圖。由圖中可知，在換熱管內安裝矩形渦流發生器改變了換熱管壁面的Nu分布，在渦流發生器后方形成了一個具有較高Nu的帶狀區域，這是因為流體流過渦流發生器后，流體跡線發生了偏移和旋轉(圖3)，加速了冷熱流體的匯合，因此換熱效率也得到了提高。由圖4(a)可知，隨著渦流發生器長高比L/H的增大，渦流發生器后高Nu帶變寬、變長，渦流發生器的強化傳熱效果增強。由圖4(b)可知，當渦流發生器攻角β≤ 30°時，隨著攻角β的增加，渦流發生器后高Nu帶變寬、變長，但是β= 30°和β=50°的高Nu帶形狀相似，即當攻角β> 30°時，渦流發生器攻角β的增加帶來的強化傳熱效果增加不明顯。

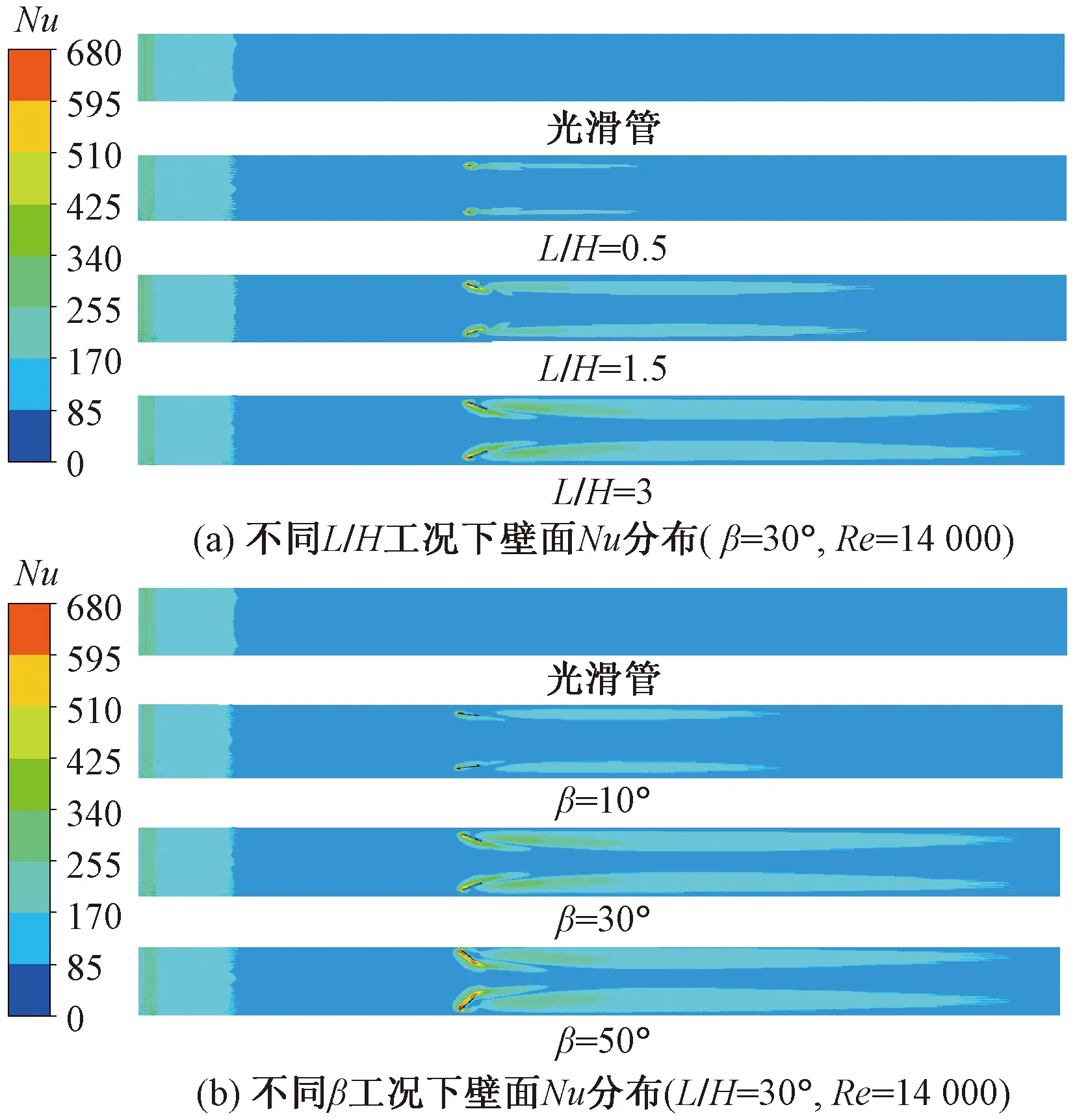
圖4 不同工況下壁面Nu分布云圖Fig.4 Nu distribution on the wall of different cases

圖5 渦流發生器周圍壁面Nu及溫度分布 (L/H=3, β=50°, Re=14 000)Fig.5 Nu and temperature distribution on the wall around the vortex generator(L/H=3, β=50°, Re=14 000)

圖5為長高比L/H= 3，攻角β= 50°，雷諾數Re= 14 000工況下渦流發生器周圍壁面Nu和溫度分布云圖。可以看出，渦流發生器前側的Nu比較高，相應的此處溫度也比較低，這是因為當流體流向矩形渦流發生器時，流體對渦流發生器前部的沖刷作用，有效地破壞了邊界層的形成，因而渦流發生器前部Nu較高，具有較好的換熱性能。在渦流發生器的下游，存在高Nu帶狀區域，此處溫度相對較低，說明渦流發生器誘導形成的渦流改善了此處的換熱性能。

x、y、z為坐標軸的方向，在規定了坐標原點的情況下， x、y、z表示距離原點的距離圖6 換熱管上6個橫截面處的流線 (L/H=3, β=30°,Re=14 000)Fig.6 The streamlines at 6 cross-sections of the heat exchange tube(L/H=3, β=30°, Re=14 000)

為了更清楚地了解渦流發生器產生的渦流結構及其與換熱管之間的相互作用，圖6展示了不同軸向位置橫截面上的流線。可以看出，在z= 0.2處(渦流發生器前端)，沒有清晰的湍流結構，在渦流發生器下游，即從z= 0.22處開始，管內產生了4個縱向漩渦，流體存在徑向速度，破壞了近壁面區域的邊界層，使得流動邊界層變薄，4個縱向渦將會把壁面的熱流體卷入中心流域，并把中心流域的冷流體帶到溫度較高的壁面，增強冷熱流體的混合，加速管內換熱，并且，旋流結構的產生，改善了換熱管內的場協同性，從而提高了換熱管的換熱效率。

2.2 渦流發生器長高比L/H對傳熱和流動特性的影響

圖7為渦流發生器攻角β= 30°時不同Re下渦流發生器L/H對Nu數的影響，與光滑管道相比，渦流發生器的使用增大了換熱管的Nu，這是因為渦流發生器的使用增加了冷熱流體的相互混合(圖3)，增強了換熱管內的場協同性(圖6)。隨著Re的增加，換熱管的Nu增大，在相同Re工況下，渦流發生器長高比L/H越大，Nu越大。隨著L/H的增大，Nu增幅越來越小，當L/H> 2后，Nu的增加不明顯。

圖8為渦流發生器攻角β=30°時，不同Re下渦流發生器L/H對摩擦因子f的影響，在管內壁面安置渦流發生器可以提高管內的換熱速率，同樣渦流的產生也會造成壓力損失，使得f增大，與光滑管道相比，渦流發生器的使用增大了換熱管摩擦因子f。換熱管摩擦因子f隨著Re的增加而減小；在相同Re工況下，渦流發生器L/H越大，f越大。

為了在等泵功基礎上評價換熱管的傳熱流動綜合性能，采用性能比較指標(performance evaluation criterion，PEC)對傳熱管的綜合性能進行分析。PEC定義為[16]

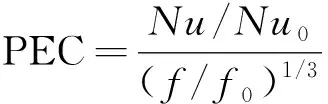
(10)

式(10)中：Nu0和f0分別為光滑圓管內平均努塞爾數和摩擦因子。

圖9為渦流發生器攻角β= 30°時，不同Re下渦流發生器L/H對PEC的影響，隨著Re的增大，PEC呈下降趨勢，說明增加流量會降低換熱管的綜合性能。但在所有使用渦流發生器的工況下，PEC都大于1，這反映了安裝在圓形管道中的渦流發生器在提高換熱效率方面的積極作用，使用渦流發生器

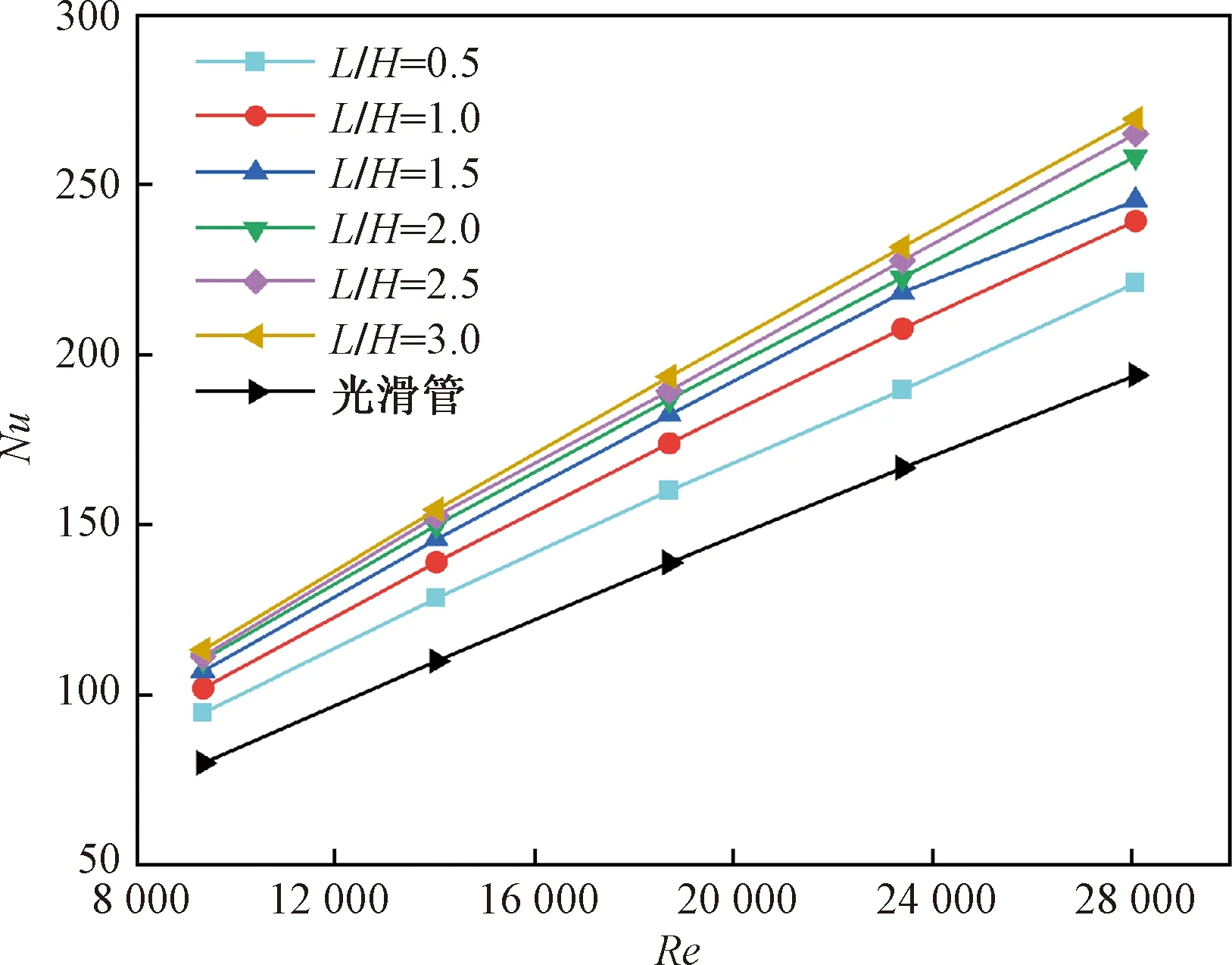
圖7 渦流發生器L/H對Nu數的影響Fig.7 Effect of vortex generator L/H on Nu

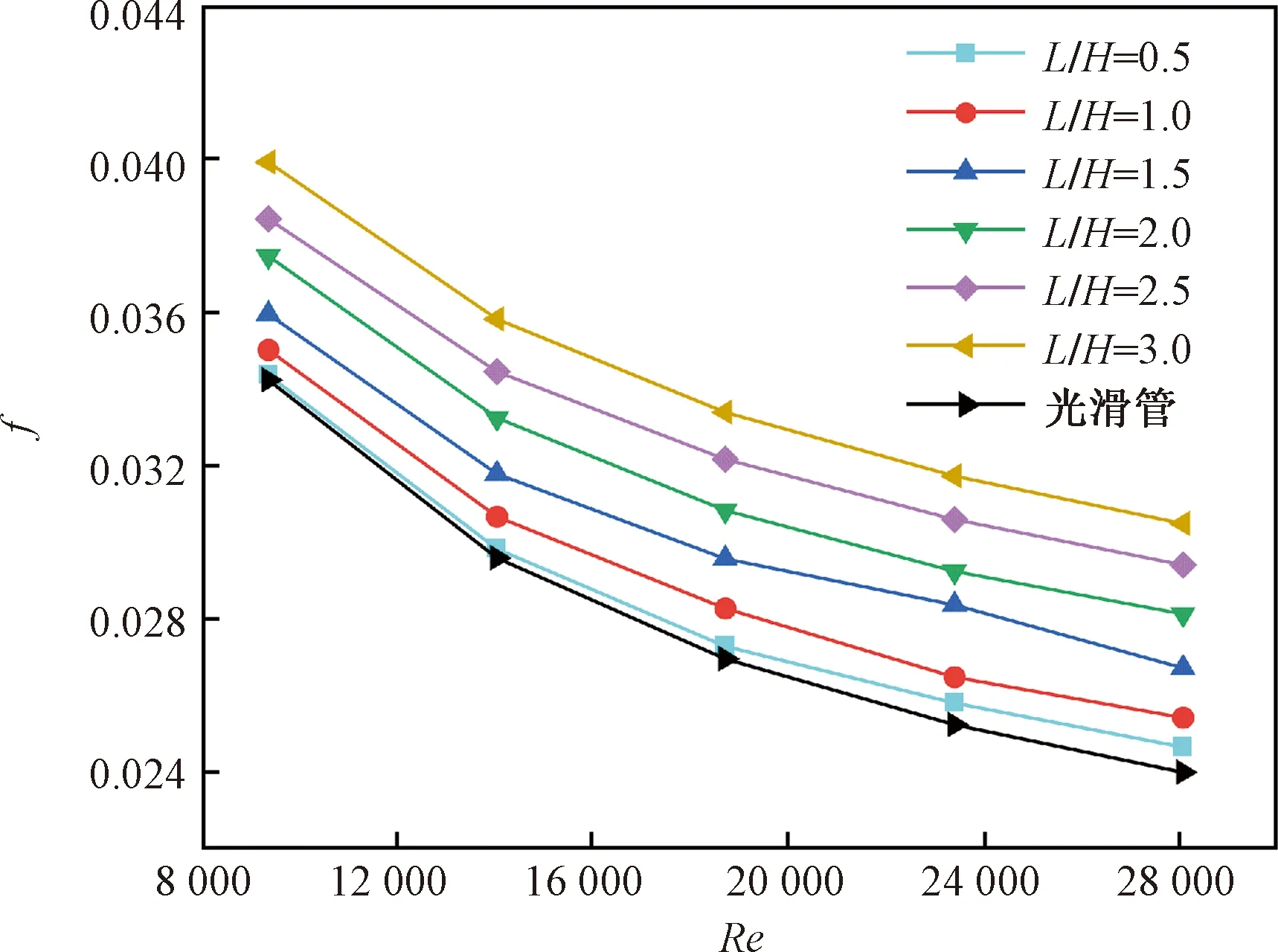
圖8 渦流發生器L/H對f的影響Fig.8 Effect of vortex generator L/H on f

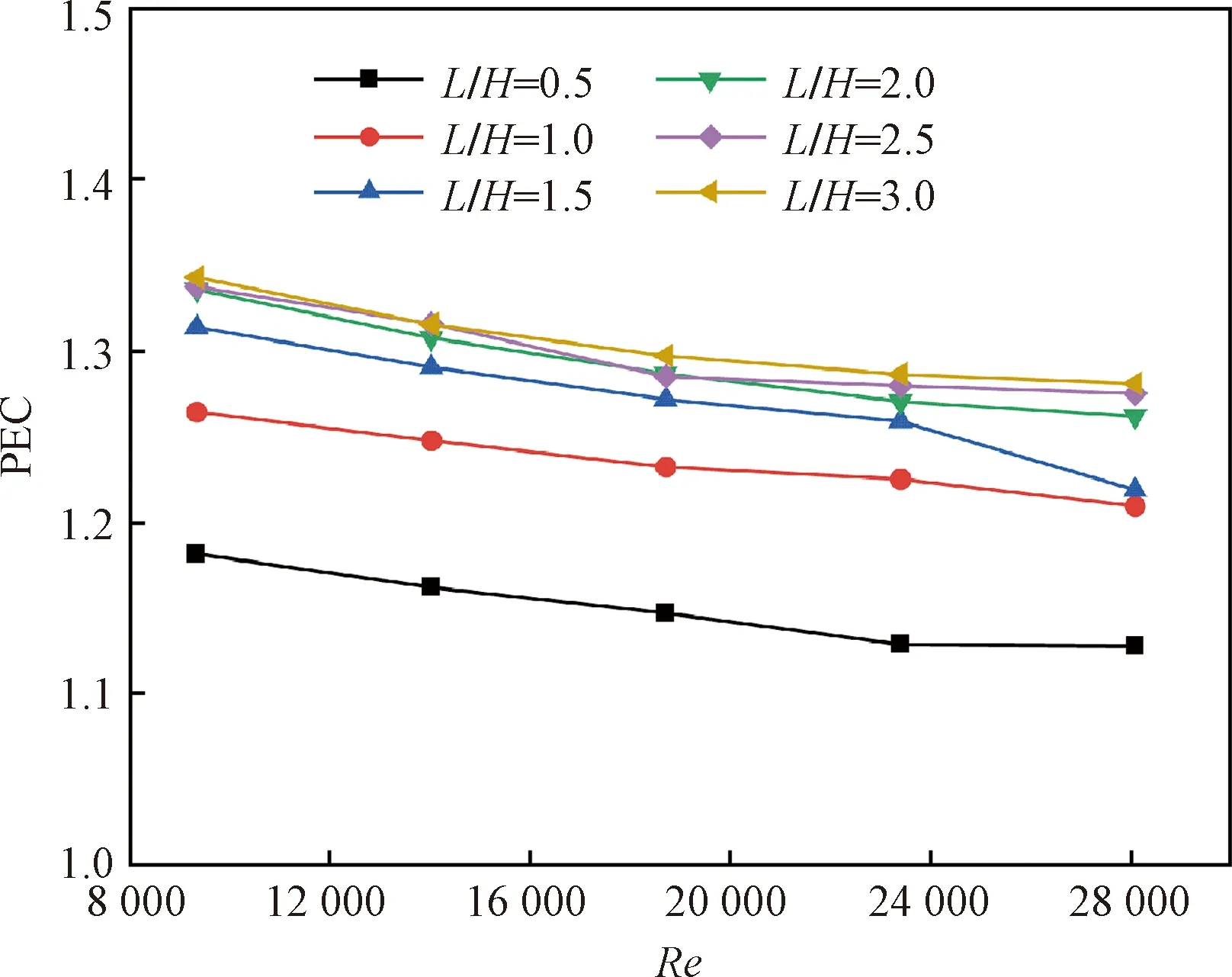
圖9 渦流發生器L/H對PEC的影響Fig.9 Effect of vortex generator L/H on PEC

的管道PEC達到1.128～1.343。在相同Re下，隨著L/H的增大，PEC的增加幅度逐漸減小，在L/H大于2之后，PEC的增加不明顯，即當L/H=2時，換熱管具有較好的綜合性能。因此渦流發生器在實際應用中，為獲得較高的換熱效率，同時避免出現較大的壓降，應采用合適的長高比。

2.3 渦流發生器攻角β對傳熱和流動特性的影響

圖10為渦流發生器L/H=3時，不同Re下渦流發生器攻角β對Nu的影響，與光滑管道相比，渦流發生器的使用增大了換熱管的Nu。隨著Re數的增加，換熱管的Nu增大。在相同Re工況下，當攻角β≤30°時，Nu隨攻角的增加而增大，這是因為隨著攻角的增加，渦流發生器后產生的螺旋狀尾跡區域增大所致(圖3)。當攻角β>30°時，隨著攻角的增大，Nu幾乎沒有變化甚至略降低，雖然更大的攻角會導致更強烈的旋流，但過大的攻角會使得渦流發生器所誘導產生縱向渦旋的渦度矢量的切向分量過小，相比較攻角β=30°而言，縱向渦旋的強度并沒有得到增強，因此，Nu的變化很小，圖4(b)也印證了這一點。

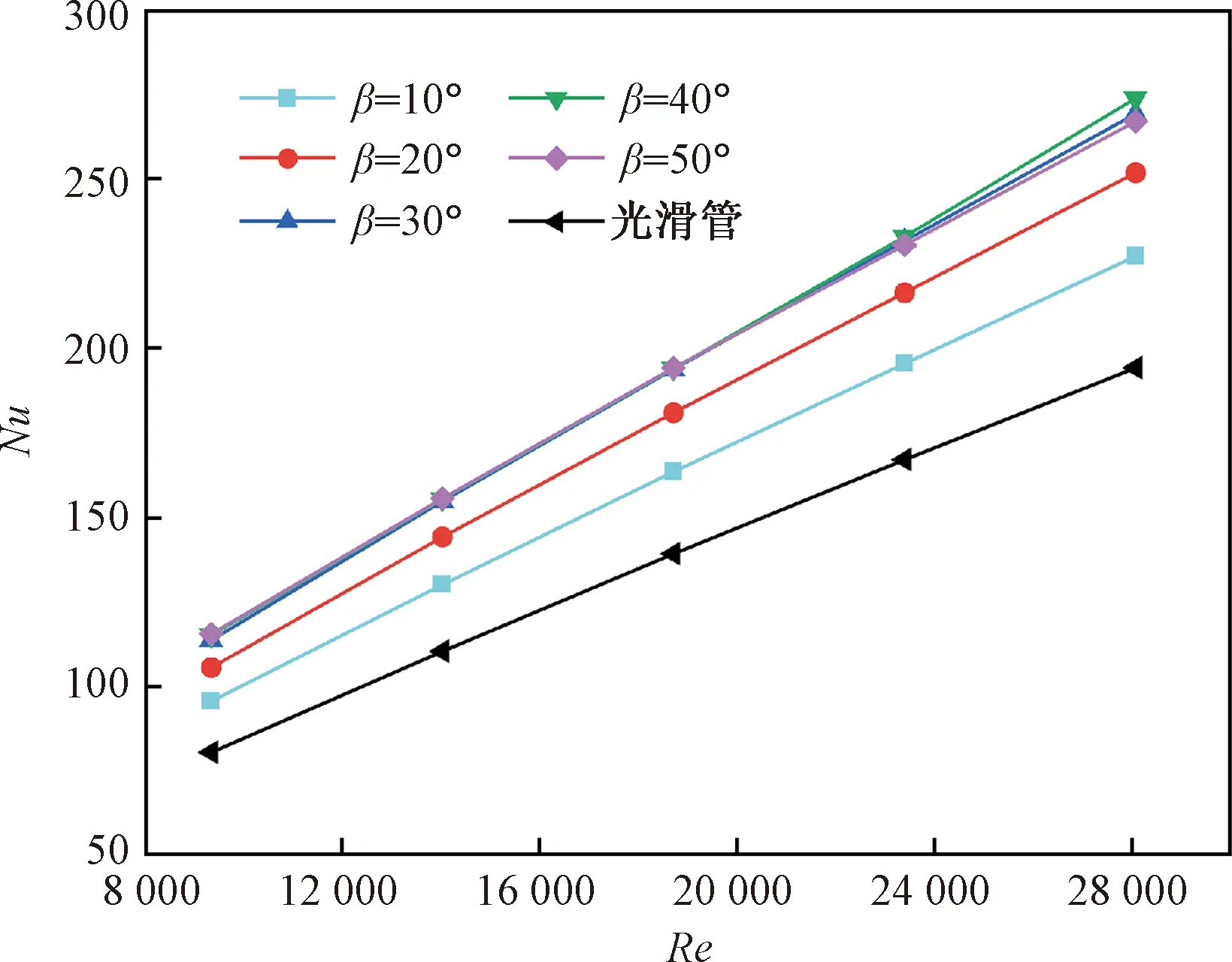
圖10 渦流發生器攻角β對Nu的影響Fig.10 Effect of attack angle β of vortex generator on Nu

圖11為渦流發生器L/H=3時，不同Re下渦流發生器攻角β對f的影響，與光滑管道相變，渦流發生器的使用增大了換熱管的f。換熱管的f隨著Re的增加而減小，在相同Re工況下，渦流發生器攻角β越大，f越大，隨著攻角β的增加，f的增幅越來越小，說明大攻角情況下，攻角的增加帶來的阻力增加不明顯。

圖12為渦流發生器L/H=3時，不同Re下渦流發生器攻角β對PEC的影響，PEC變化范圍為1.149～1.351，均大于1，這反映了安裝在圓形管道中的渦流發生器在提高換熱效率方面的積極作用。隨著Re數的增大，PEC呈下降趨勢，在相同Re數下，隨著攻角β的增大，PEC先增大后減小，當攻角β=30°時，多數工況下PEC具有最大值，換熱管具有最佳綜合性能。

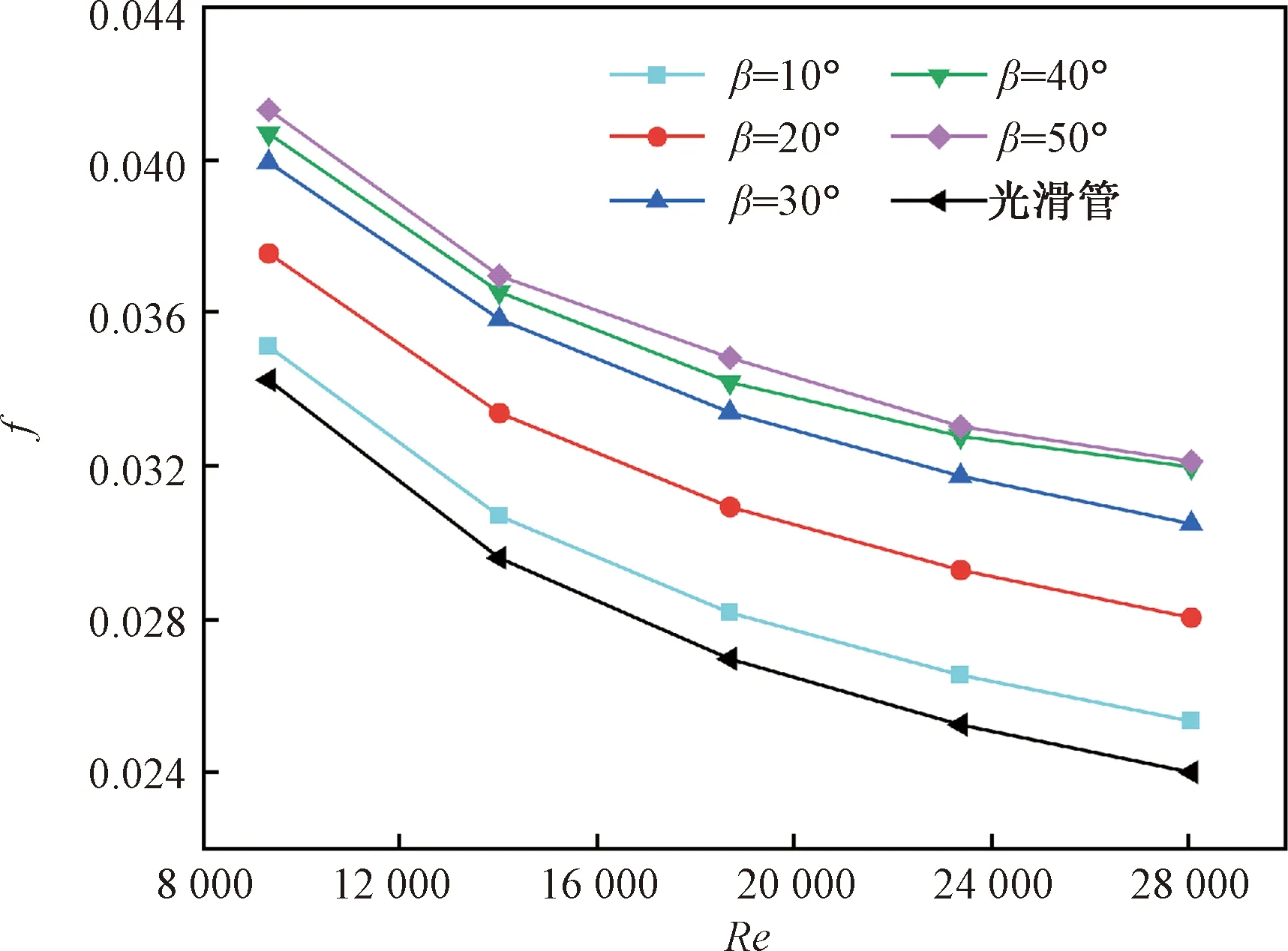
圖11 渦流發生器攻角β對f的影響Fig.11 Effect of attack angle β of vortex generator on f

圖12 渦流發生器攻角β對PEC的影響Fig.12 Effect of attack angle β of vortex generator on PEC

3 結論

對內置矩形渦流發生器的圓形換熱管進行了數值模擬研究，得到了渦流發生器長高比L/H和攻角β對Nu、f和PEC的影響規律，通過對換熱管內的流動和傳熱性能進行分析，得出如下結論。

(1)流體介質在渦流發生器下游產生了螺旋形流跡，換熱管內產生了4個縱向漩渦，加速了冷熱流體的匯合，改善了換熱管內的場協同性，提高了換熱管的換熱效率。

(2)在渦流發生器攻角β=30°，相同Re工況下，隨渦流發生器L/H的增大，Nu增幅越來越小；渦流發生器L/H越大，f越大；隨著L/H的增大，PEC的增加幅度逐漸減小，當L/H=2時，換熱管具有較好的綜合性能。

(3)在渦流發生器長高比L/H= 3，相同Re數工況下，攻角β對Nu和f均有較大的影響，隨著攻角β的增大，PEC先增大后減小，當攻角β=30°時，多數工況下PEC具有最大值，換熱管具有最佳綜合性能。