GLOBAL STRUCTURE OF A NODAL SOLUTIONS SET OF MEAN CURVATURE EQUATION IN STATIC SPACETIME*

School of Economics and Finance,Shanghai International Studies University,Shanghai 201620,China

E-mail: loha_u@shisu.edu.cn

Guowei DAI (代國偉)?

School of Mathematical Sciences,Dalian University of Technology,Dalian 116024,China

E-mail: daiguowei@dlut.edu.cn

Abstract By bifurcation and topological methods,we study the global structure of a radial nodal solutions set of the mean curvature equation in a standard static spacetime with a 0-Dirichlet boundary condition on the unit ball.According to the behavior of H near 0,we obtain the global structure of sign-changing radial spacelike graphs for this problem.

Key words bifurcation;static spacetime;mean curvature operator;nodal solution

1 Introduction

We start by recalling that a spacetimeMis static relative to an observer fieldU,provided theUis irrotational and there is a smooth positive functionaonMsuch thataUis a Killing vector field.Let Ω ?RNwithN≥1 be a domain and letabe a smooth positive function on Ω.Denote by M theN+1-dimensional product manifoldI×Ω endowed the Lorentzian metric

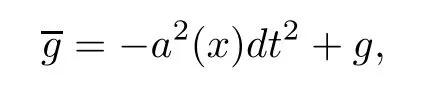
wheregis a metric on Ω.From Lemma 12.37 of [23],we know that M is static relative to?t/a.In particular,M is the Schwarzschild spacetime if Ω is spherically symmetric andg=E2(r)dr2+r2dσ2(see [19,22,23]),withE(r) being a smooth positive function onanddσ2being the usual metric of the sphere SN-1.

For anyu∈C2(Ω),consider its graph

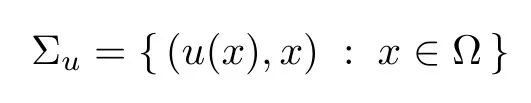
in the standard static spacetimeM:=(I× Ω),which is spacelike,i.e.,the induced metric on Σuis Riemannian if and only ifa|?u|＜1 holds on all Ω.IfHis the mean curvature of the spacelike graph Σu,the functionuis a solution of the mean curvature spacelike hypersurface equation

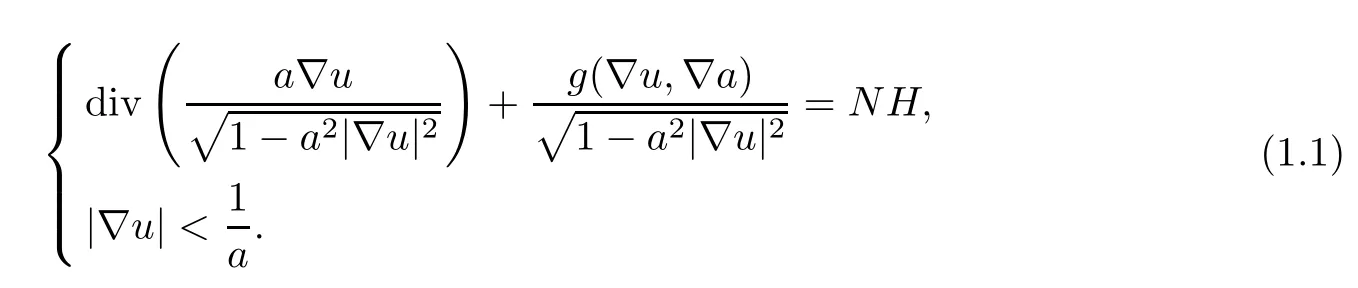
Whena≡1,H≡0 and Ω=RN,equation (1.1) reduces to the well-known maximal hypersurface equation in Lorentz-Minkowski spacetime.For this case,Calabi [5] proved that the only entire solutions are the affine functions forN≤4.Cheng and Yau [7] extended this result for allN.For whena≡1 andHis a non-zero constant,some celebrated results for equation (1.1) were obtained by Treibergs [25].For whena≡1,Ω is a bounded domain,andHis a bounded function defined on Ω × R,Bartnik and Simon [1] proved that equation (1.1)with a Dirichlet boundary condition has a strictly spacelike solution.By topological degree,or critical point theory,the authors of [4,9] studied the nonexistence,existence and multiplicity of positive solutions for the case ofa≡1 and Ω being a bounded domain.For whena≡1 and Ω=BR:=BR(0)=｛x∈RN: |x|＜R｝withR ＞0,Bereanu,Jebelean and Torres [2,3]obtained some existence results for positive radial solutions of equation (1.1),withu=0 on?Ω.Recently,for whena≡1,the authors of [6,11,17] studied the nonexistence,existence and multiplicity of positive or sign-changing radial solutions of equation (1.1) withu=0 on?Ω andNH=-λf(x,s) on the unit ball or an annular domain via the bifurcation method;these results were extended to the general domain in [13–15].

The aim of this paper is to investigate the existence of a radially symmetric nodal solution for equation (1.1) on the unit ballB,mainly by the bifurcation method.To this end,we consider the 0-Dirichlet boundary value problem

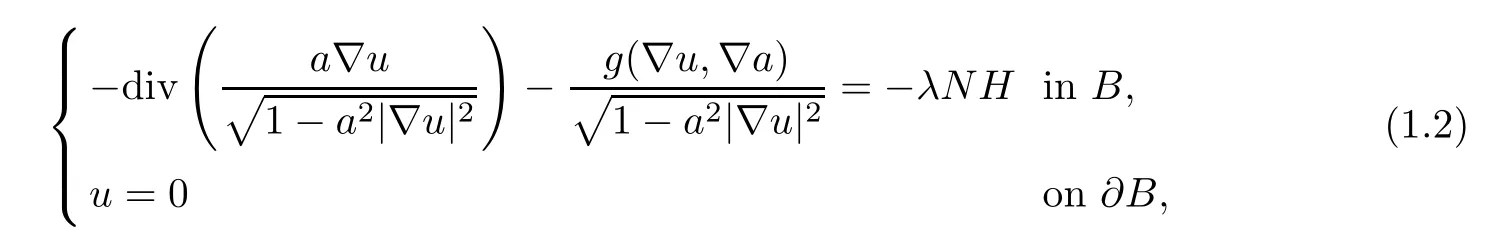
whereλis a nonnegative parameter,a:→R is a smooth positive radially symmetric function,andH:× [-δ,δ] →R is a continuous function that is radially symmetric with respect toxwith some positive constantδto be determined later.Following [19],problem (1.2) can be reduced to the following boundary value problem:

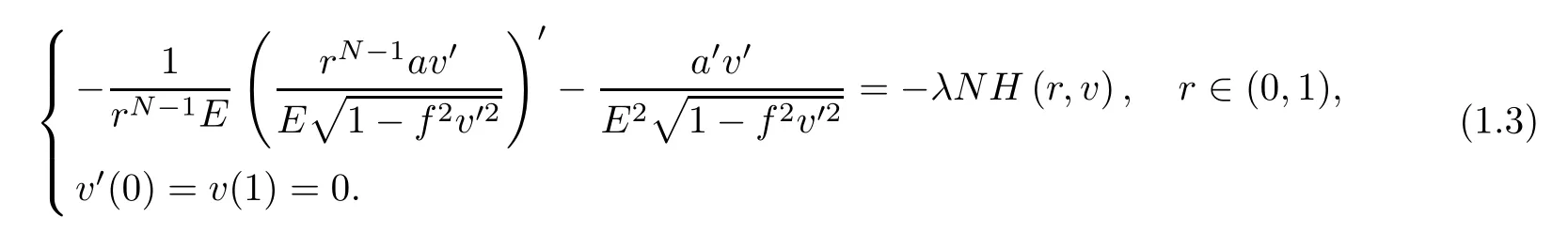
Herer=|x|,v(r)=u(|x|),a(r)=a(|x|) andf=a/E.Letting,since the graph associated tovis spacelike,we deduce that ‖v‖∞＜δ.

It is well known (see,for example,[8,21,26]) that the linear eigenvalue problem

possesses infinitely many eigenvalues 0＜λ1＜λ2＜···＜λk＜···.All of these are simple,and the eigenfunctionφk(k∈N) corresponding toλkhas exactlyk-1 simple zeros in (0,1).

Theorem 1.1Assume thatH(r,t)t ＜0 for anyr∈[0,1],t∈(-δ,δ) {0},and there existsH0∈(0,+∞] such that

The existence of a nodal solution of problem (1.3) can be easily seen from Theorem 1.1.By an argument similar to that of Theorem 1.1,we can also show that the conclusions of Theorem 1.1 are valid for equation (1.1) on any annular domain with the Robin boundary condition.

The rest of this paper is arranged as follows: in Section 2,we show a preliminary lemma.The proof of Theorem 1.1 will be given in the last section.

2 A Preliminary Lemma

Clearly,problem (1.3) is equivalent to

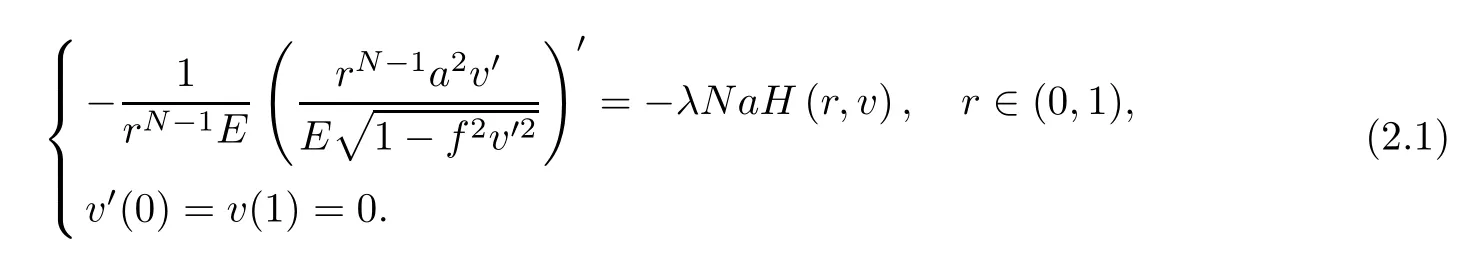
Then,we have the following existence and uniqueness result for problem (1.3):

Lemma 2.1Assume that there exists a constantM ＞0 such that

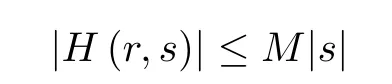
for anyr∈[0,1] ands∈[-δ,δ].For any solutionvof problem (1.3) having a double zero,v≡0.

ProofLetvbe a solution to problem (2.1) and letr*∈[0,1] be a double zero.Note that

Ifr*=0,we have that

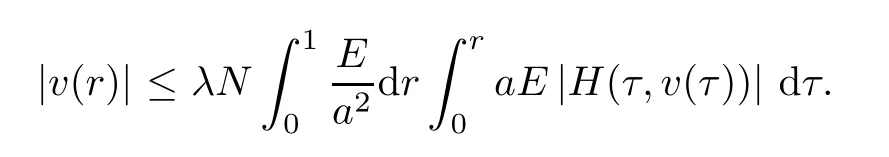
Thus,we have that

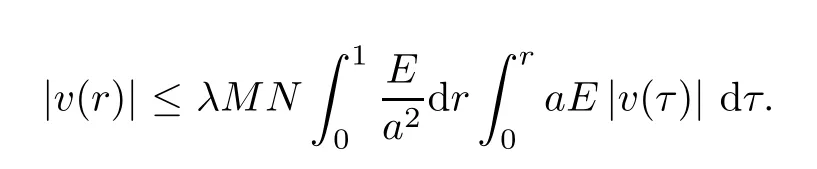
By the Gronwall-Bellman inequality [10,Lemma 2.1],we have thatv≡0 on [0,R].

Next,we assume thatr*＞0.We first considerr∈[0,r*].Reasoning as above,we obtain that

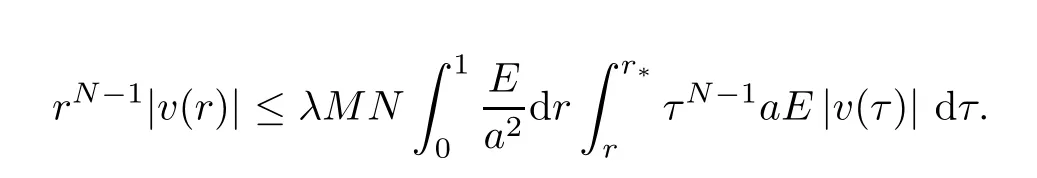
It follows from the Gronwall-Bellman inequality [10,Lemma 2.2] thatrN-1|v(r)| ≡0 on [0,r*].Furthermore,the continuity ofvshows thatv≡0 on [0,r*].On the other hand,forr∈[r*,1],in the same manner,we have that

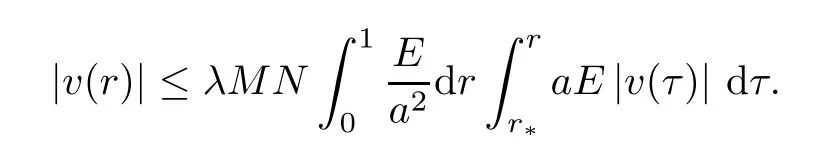
Again by the Gronwall-Bellman inequality [10,Lemma 2.1],we have thatv≡0 on [r*,1].Therefore,we get thatv≡0 on [0,R]. □

3 Proof of Theorem 1.1

For anyv∈X,define

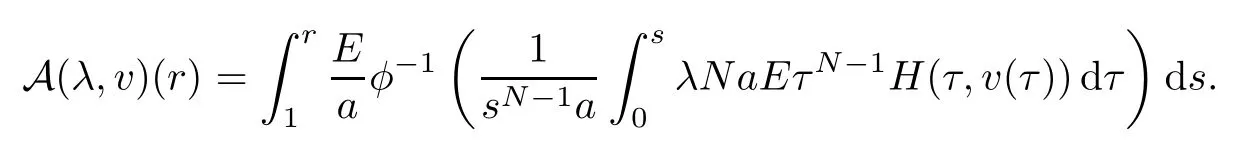
It is easy to verify that finding a solution to problem (1.3) is equivalent finding a fixed point of A.From the Arzelà-Ascoli Theorem,we know that A(λ,·) :XXis completely continuous.

Proof of Theorem 1.1(a) SinceH0=1,for anyw∈X{0},we have that

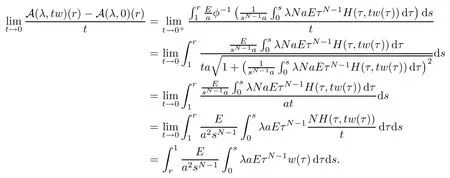
Then,by the implicit function theorem,the necessary condition for (μ,0) to be a bifurcation point of problem (1.3) is that

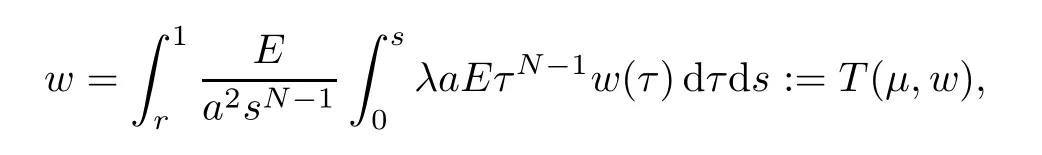
which is equivalent to eigenvalue problem (1.4).Thus,μ=λkfor somek∈N.

Obviously,I-T(λ,·) is a completely continuous vector field.Therefore,the Leray-Schauder degree deg (I-T(λ,·),Bγ(0),0) is well defined for arbitraryγ-ball Bγ(0) :={v∈X: ‖v‖＜γ}andλλk.From [18,Theorem 8.10],we have that

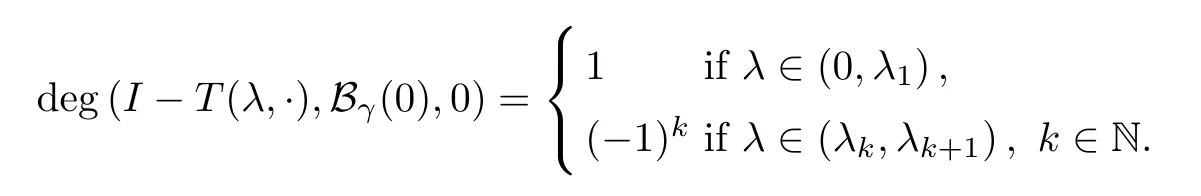
Lettingξ(r,s)=-NH(r,s)-s,we have that

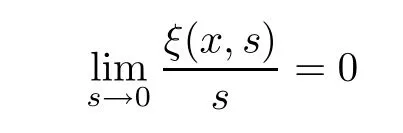
uniformly forr∈(0,1).Then,problem (1.3) is equivalent to

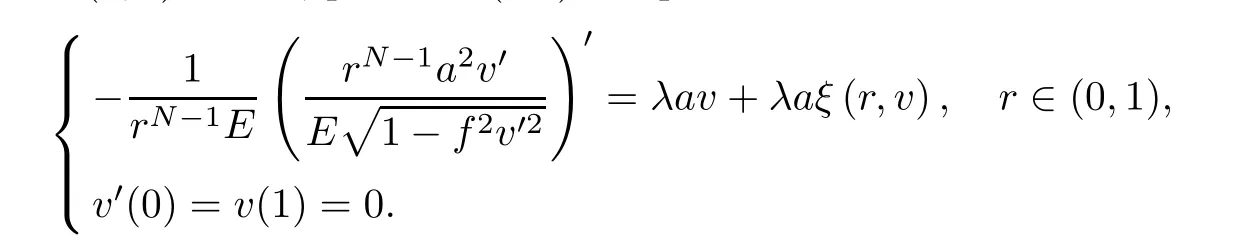
For anyt∈[0,1],we consider the following problem:

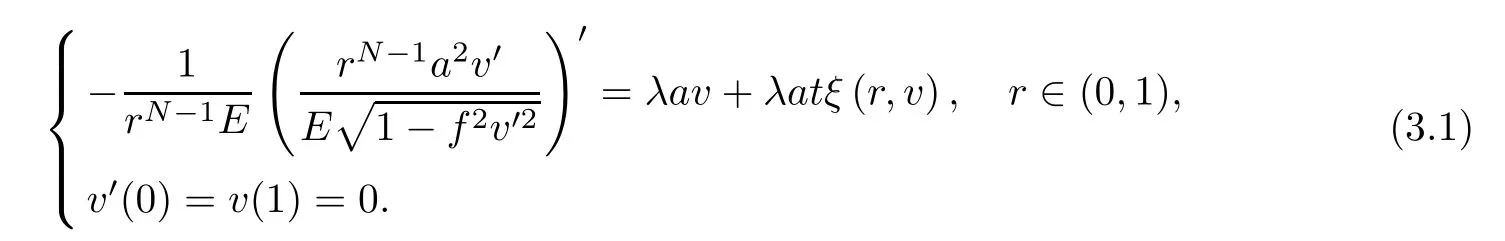
Obviously,problem (3.1) is equivalent to

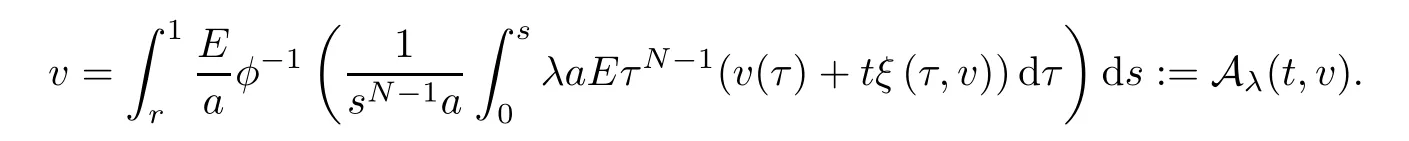
Clearly,Aλ: [0,1]×XXis completely continuous.

Let

Furthermore,it follows from (3.2) that

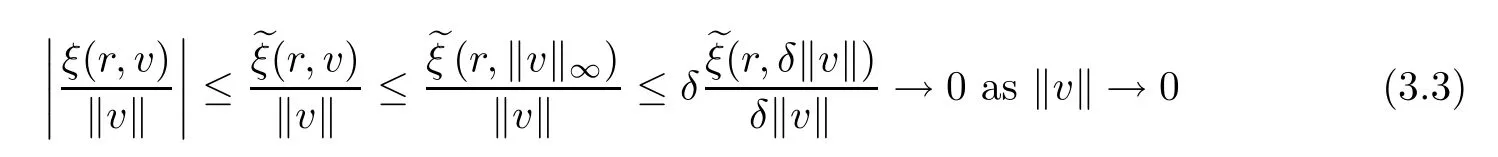
uniformly inr∈(0,1).We claim that the Leray-Schauder degree deg (I-Aλ(t,·),Bγ(0),0)is well defined forλ≠λkandγsmall enough.Suppose,on the contrary,that there exists a sequence {vn} such thatvn=Aλ(t,vn) and ‖vn‖ →0 asn→+∞.Lettingwn=vn/‖vn‖,we have thatwnsatisfies

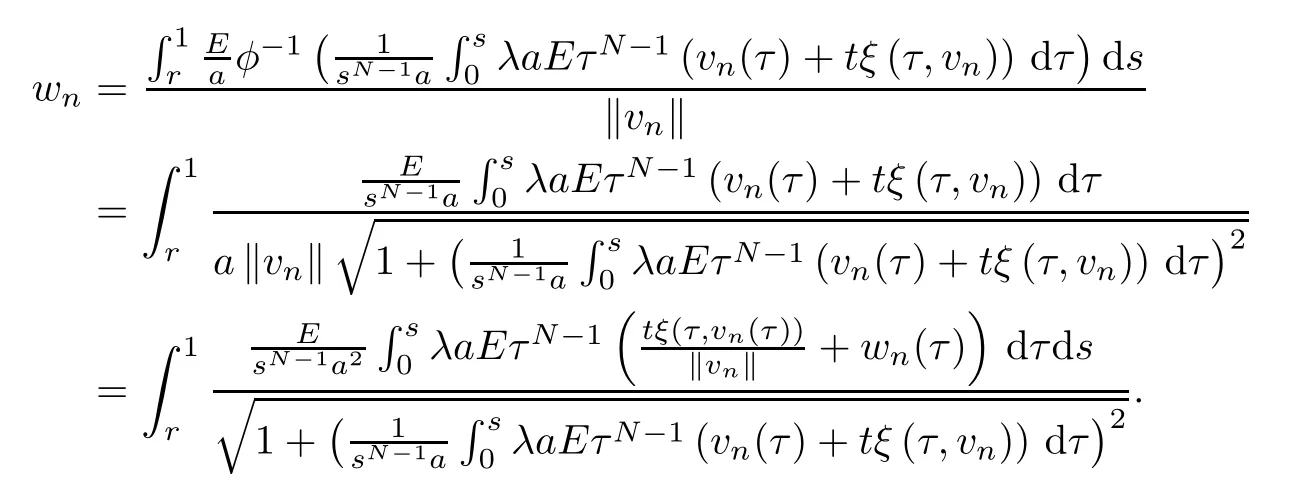
From the compactness of Aλ,up to a subsequence,we have thatwn→winXasn→+∞.Lettingn→+∞in the above equality,using (3.3) and the continuity of Aλ,we obtain that

Clearly,one has that ‖w‖=1.Thus,λis an eigenvalue of problem (1.4),which is a contradiction.By the invariance of the degree under homotopies,we find that

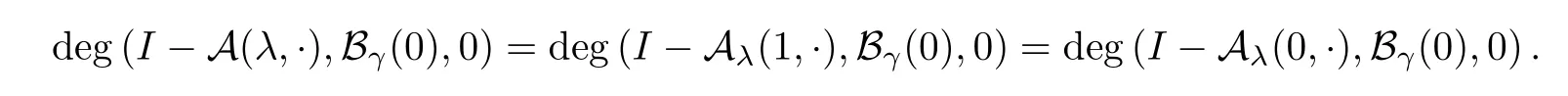
For anyt∈[0,1],we consider

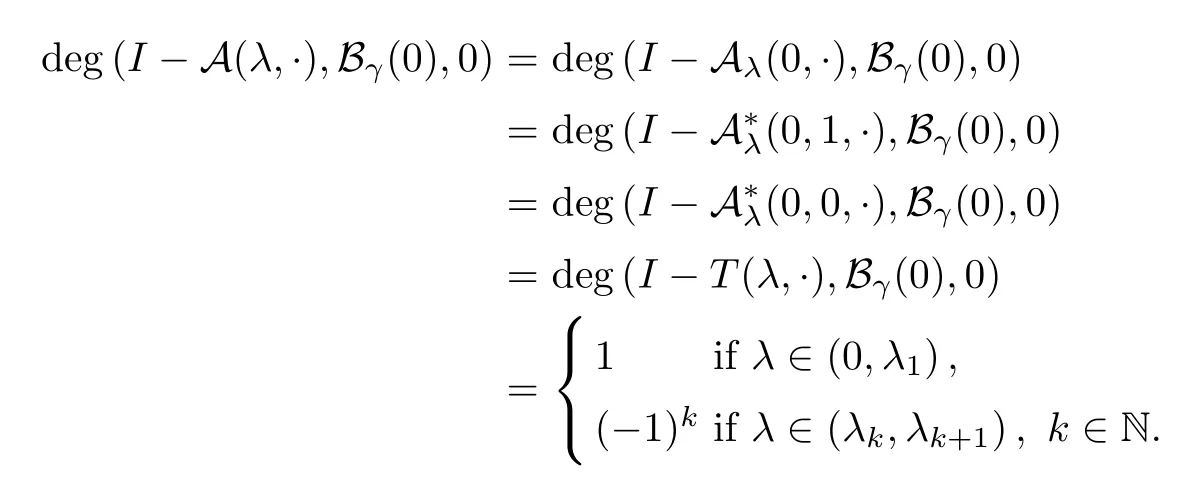
Applying Proposition 2.1 of [16] with O=R × B1(0),there exists a maximum continuum Ck+of nontrivial solutions of problem (1.3) bifurcating from (λk,0) which satisfies at least one of the following three properties:

(i) Ck+is unbounded in O;

(ii) meets R ×?B1(0);

(iii) Ck+∩(R {λi}×{0})≠?.

From [20,Theorem 2.1 and Theorem 4.1],we get that there exists a positive constantθdepending onN,a,E,Hand Ω such that ‖v‖ ≤1 -θ.Thus,the case (ii) does not occur.Similarly as to Lemma 1.24 of [24],we can show that if (λ,v) ∈Ck+and is near (λk,0),thenv=αφk+wwithw=o(|α|) forαnear 0.It follows that there exists an open neighborhood N of (λk,0) such that

To obtain another component,we consider the following auxiliary problem:

(b) For anyn∈N,define

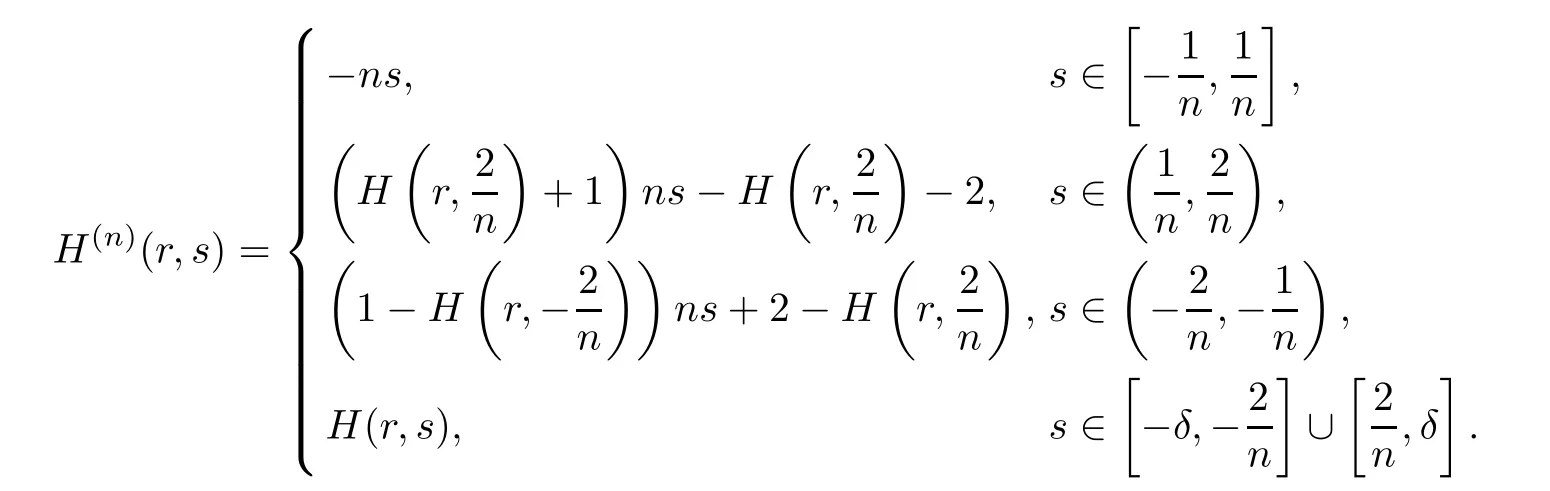
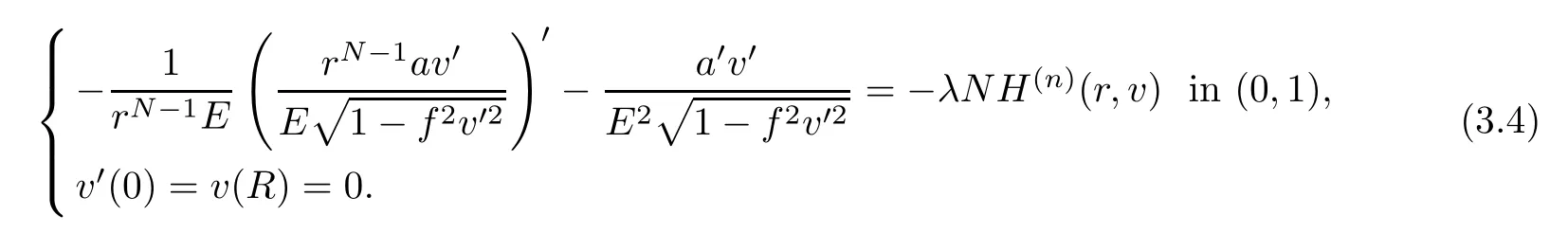
By (a),ν∈{+,-},there exists a sequence of unbounded continuaof the set of nontrivial solutions of problem (3.4) emanating from (λk/n,0) such that