基于改進PSO-DE融合算法優化LSSVM的短期風功率預測

張志浩，熊文潔，鐘 文，印云剛，劉 闖，郭文超

（1.國網湖北省電力有限公司荊門供電公司，湖北 荊門 448000；2.國網湖北省電力有限公司荊州供電公司，湖北 荊州 434000；3.三峽大學電氣與新能源學院，湖北 宜昌 443000）

0 引言

2021 年政府工作報告中我國明確提出了“碳達峰”和“碳中和”的目標，在“雙碳”背景下，政府倡導開發和使用清潔能源［1-2］。風能是一種清潔能源，也是一種可再生能源，風力發電的大力推廣能夠減少碳排放量，緩解能源危機［3-4］。我國幅員遼闊，海岸線狹長，陸海風能資源都十分豐富，但風功率變化具有較大的隨機波動性，在并網時會對電力系統造成一定沖擊［5-6］。為此，深入挖掘風功率數據之間的關系，建立較準確的風功率預測模型，實現風功率的精確預測，對提高電力系統運行安全穩定性和風能利用效率具有重要意義。

文獻［7］為了降低風功率數據的波動性，以風速、風向和風功率歷史數據為輸入參量，在融合卷積神經網絡中引入傳統門控循環單元，建立基于深度門控循環單元神經網絡的短期風功率預測模型，并用工程實例驗證了模型在運算速度和預測準確度方面優勢。文獻［8］通過分析確定風功率的主要影響因素為風速、風向正弦和余弦，采用自適應策略對人工蜂群算法（Artificial Bee Colony，ABC）進行改進，以風速、風向和風功率歷史數據為輸入量，利用ABC算法對BP 神經網絡的權值和閾值進行優化，建立ABCBP 風功率預測模型，采用實際算例驗證了模型的正確性。文獻［9］針對傳統歷史數據預測方法的不足，首先采用帶降噪處理的自動編碼機構建深度神經網絡模型，然后應用深度遷移方法挖掘特征數據之間的隱含聯系，最后根據地理位置和相似特征提取相似數據，建立了風功率預測深度遷移模型。文獻［10］為了降低風功率歷史數據的波動性，采用經驗小波變換（Empirical Wavelet Transform，EWT）對原始風功率數據進行分解，采用量子粒子群算法（Quantum Particle Swarm Optimization，QPSO）對核極限學習機（Kernel Extreme Learning Machine，KELM）的參數進行優化，建立了基于EWT-QPSO-KELM 的風功率預測模型。上述模型雖然能夠實現風功率的預測，但預測精度有待進一步提高。

采用慣性權系數、粒子初始化規則調整和越界粒子變異操作等策略對粒子群差分融合算法進行改進，利用改進粒子群差分融合算法對最小二乘支持向量機的參數進行優化，建立基于改進粒子群差分融合算法優化最小二乘支持向量機的短期風功率預測模型，采用風電場實際運行數據對模型的正確性和實用性進行驗證。

1 算法介紹

1.1 最小二乘支持向量機

最小二乘支持向量機（Least Squares Support Vector Machine，LSSVM）是一種典型的機器學習方法，常用于解決非線性分類、回歸問題，其特點是對于小樣本數據也具有較高的計算精度［11］。

LSSVM 算法回歸原理為［12］：設某一訓練集為T={(xi，yi)|i=1，2，…，n}，其中xi∈Rd，表示輸入變量，yi∈R，表示輸出量，n為樣本容量，LSSVM 的回歸思想是尋找最優函數f∈F={f|f：Rd→R}完成對訓練集的回歸擬合。

LSSVM 利用非線性映射φ：Rd→Rk(k≥d)將低維空間中的樣本數據映射到高維空間，令高維空間中的回歸方程為

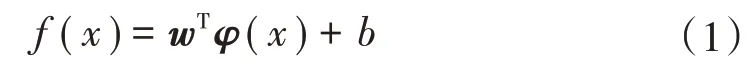
式中：w∈Rk為權值向量；b∈R為閾值。

根據結構風險最小化原則，引入松弛變量，則回歸問題的目標函數及相應的約束條件為

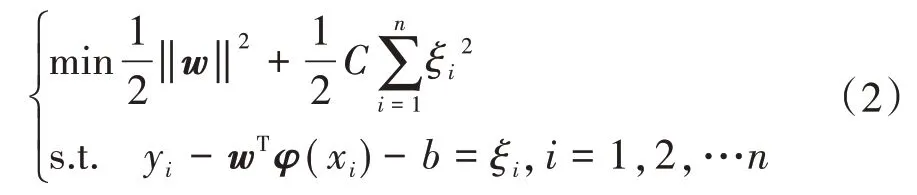
式中：ξi為松弛變量，ξi≥0；C為懲罰因子，C＞0。

為了求解式（2），將拉格朗日乘子引入，可得拉格朗日函數，具體如下

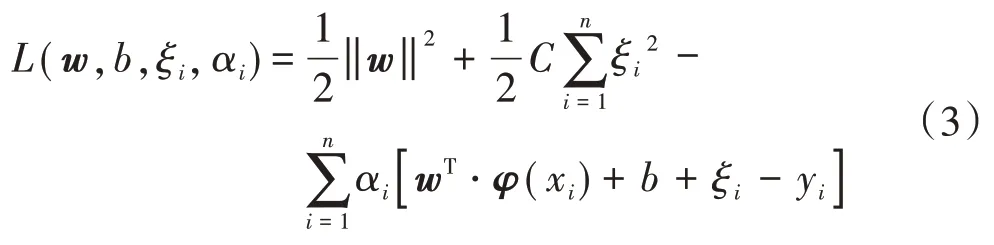
式中：αi為拉格朗日乘子，αi≥0。

拉格朗日函數取得極值時，應滿足關系

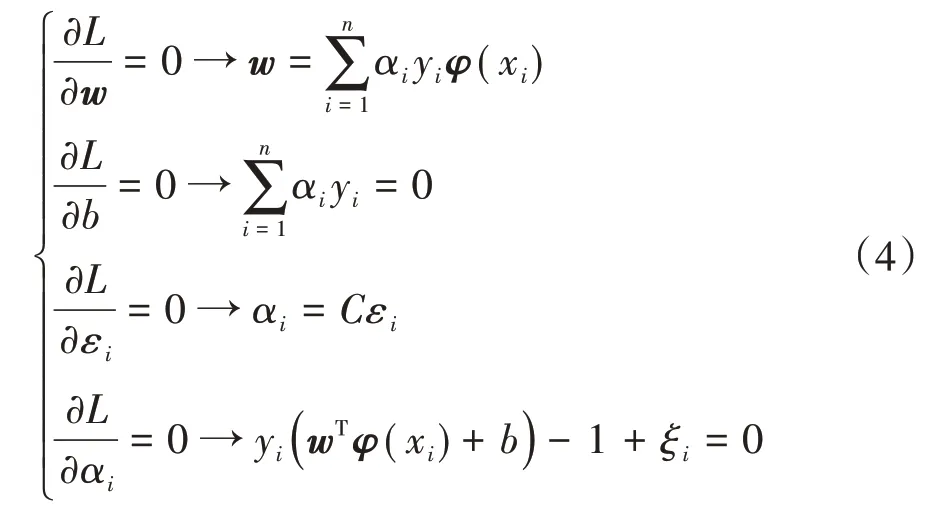
將式（3）中的w和ξi消去，可得線性方程組：

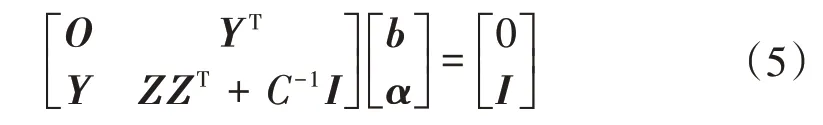
式中：O為全零矩陣。

式（5）中，有

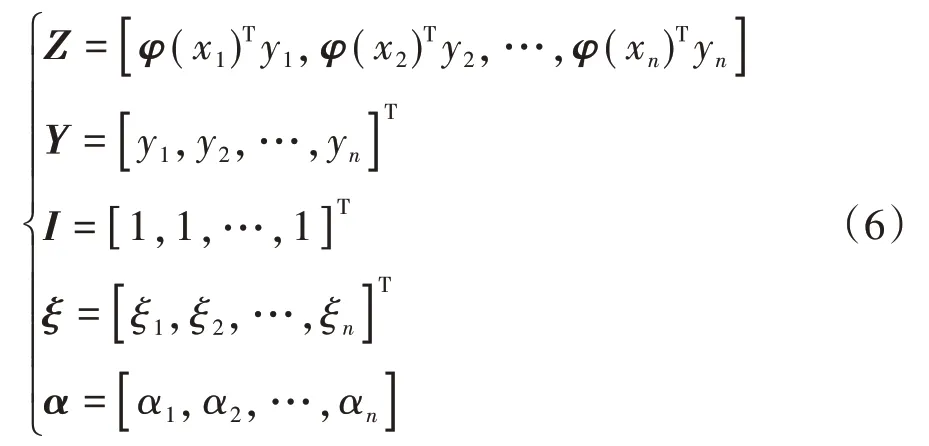
令Ω=ZZT，依據Mercer 條件，引入核函數K(xi，xj)=φ(xi)T·φ(xj)，則有

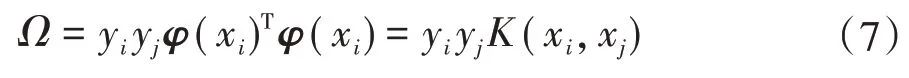
綜合式（5）—式（7），可得：

利用最小二乘法求解式（8），即可得到LSSVM的回歸函數為

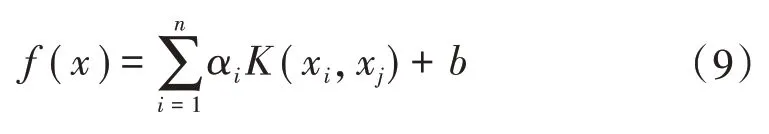
核函數的形式有多種，常用的有多項式核函數、多層感知器核函數、雙曲正切核函數和高斯徑向基核函數［13］。由于高斯徑向基核函數的對稱性、可導性和光滑性均較好，具有較強的泛化能力，因此采用高斯徑向基核函數，其表達式為

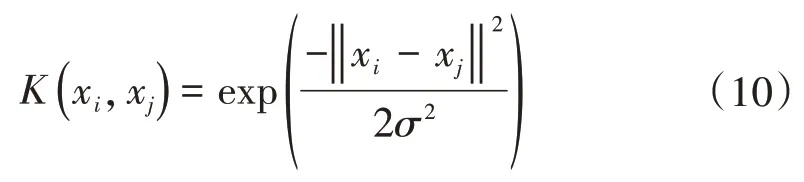
式中：σ為核函數參數。

研究表明，LSSVM 的回歸擬合效果受懲罰因子C和核函數參數σ的影響很大［14］，為了提高LSSVM的回歸精度，需要采用合適的算法對C和σ進行尋優。

1.2 改進粒子群差分進化融合算法

粒子群—差分進化（Particle Swarm Optimization-Differential Evolution，PSO-DE）融合算法是結合粒子群算法和差分進化算法尋優特點提出的一種優化算法［15］。PSO 算法和DE 算法雖然都能完成尋優，但兩種算法的個體生成過程不同，PSO-DE 融合算法能夠使兩個種群中的信息更好地交流，在迭代過程中始終選擇兩個種群的整體極值進入下一代，避免單一算法在尋優過程中陷入局部最優。PSO 算法［16］和DE算法［17］的群體極值可表示為

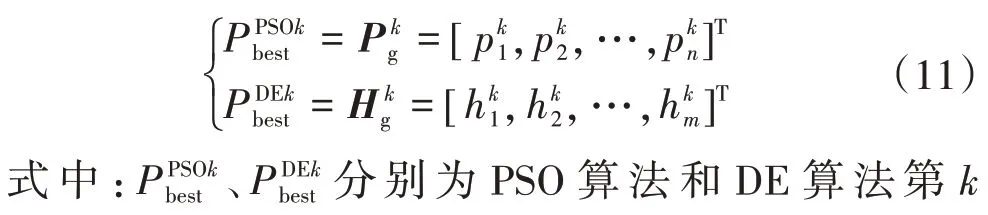
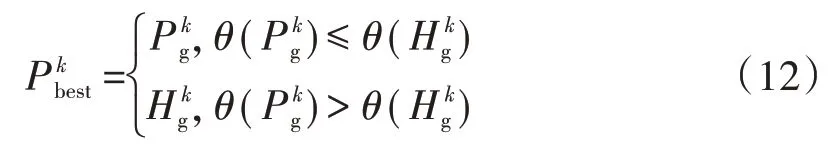
式中：Pt為適應度函數值。

PSO-DE 融合算法雖然融合了PSO 算法和DE 算法的尋優特點，解決了算法陷入局部最優的問題，為了進一步提高算法的計算精度，從三個方面對PSODE融合算法進行改進。

1）慣性權系數調整。在PSO-DE 融合算法中，慣性權系數被設置為固定值，為了增強算法前期的全局搜索能力和后期的局部尋優能力，對慣性權系數進行如下調整，具體公式為

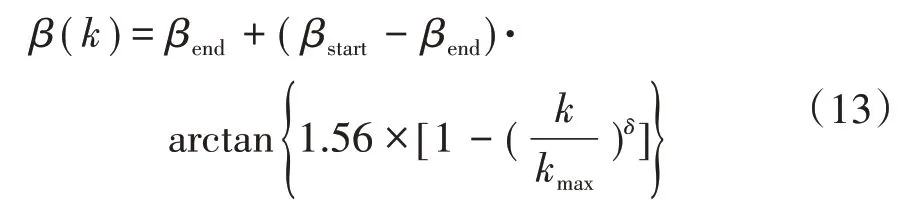
式中：β(k)為第k次迭代時的慣性權系數；βstart、βend分別為慣性權系數的初值和終值；δ為控制因子。

2）越界粒子變異操作。PSO-DE 融合算法在尋優過程會出現粒子越界的現象，常規方法是使越界粒子的速度等于邊界值，這樣會降低粒子的多樣性，降低算法的全局搜索能力。為此，對越界粒子執行變異操作。

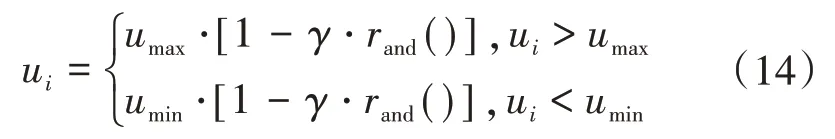
式中：γ為變異率；rand()為［0，1］之間的隨機數。

3）粒子初始化規則調整。為了使PSO-DE 融合算法中不同種群間更好地信息交流，PSO 算法和DE 算法中的元素應當屬于同一區間[zmin，zmax]，為了保持種群多樣性，將粒子初始化規則進行如下調整。

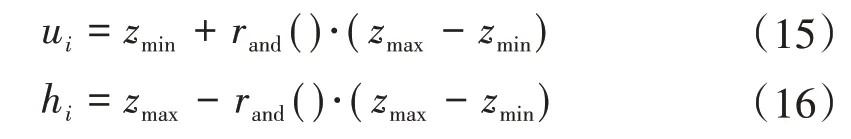
式中：ui、hi分別為PSO算法和DE算法種群的初值。

2 風功率預測模型

2.1 構建訓練樣本

風功率具有很大的隨機性和不確定性，影響風功率變化的因素（風速、溫度、氣壓、海拔、地形等）多且復雜，很難找出這些因素與風功率變化的具體關系，研究表明，風功率的變化具有混沌屬性［18］，即風功率是隨著時間的變化而變化的，前幾個時刻的功率值會影響下一時刻的功率變化。將風功率隨時間變化的序列記作{P1，P2，…，Pt}，t時刻的風功率受前m個時刻風功率的影響，則t時刻的風功率Pt可表示為

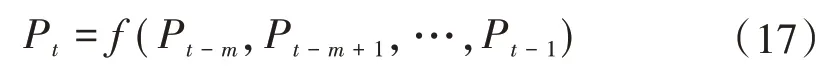
式中：f為函數關系；m為嵌入維數［19］。嵌入維數的取值恰當與否對風功率預測的準確性起決定性作用。

根據式（17）可以得出，風功率預測模型的輸入量、輸出量和嵌入維數之間的關系如表1所示。

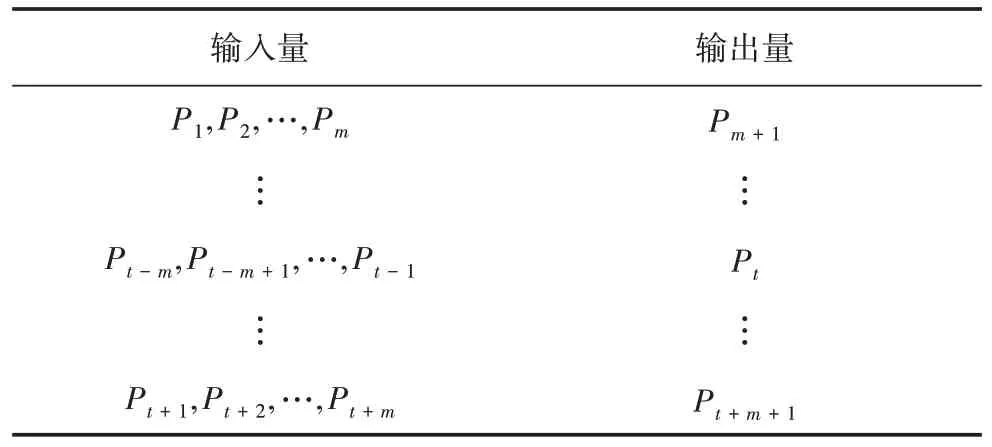
表1 風功率預測模型輸入量與輸出量關系

2.2 模型的建立

采用PSO-DE 融合算法對LSSVM 的懲罰參數和核函數參數進行優化，建立基于改進PSO-DE 融合算法優化LSSVM 的短期風功率預測模型，建模步驟如下，建模流程如圖1所示。

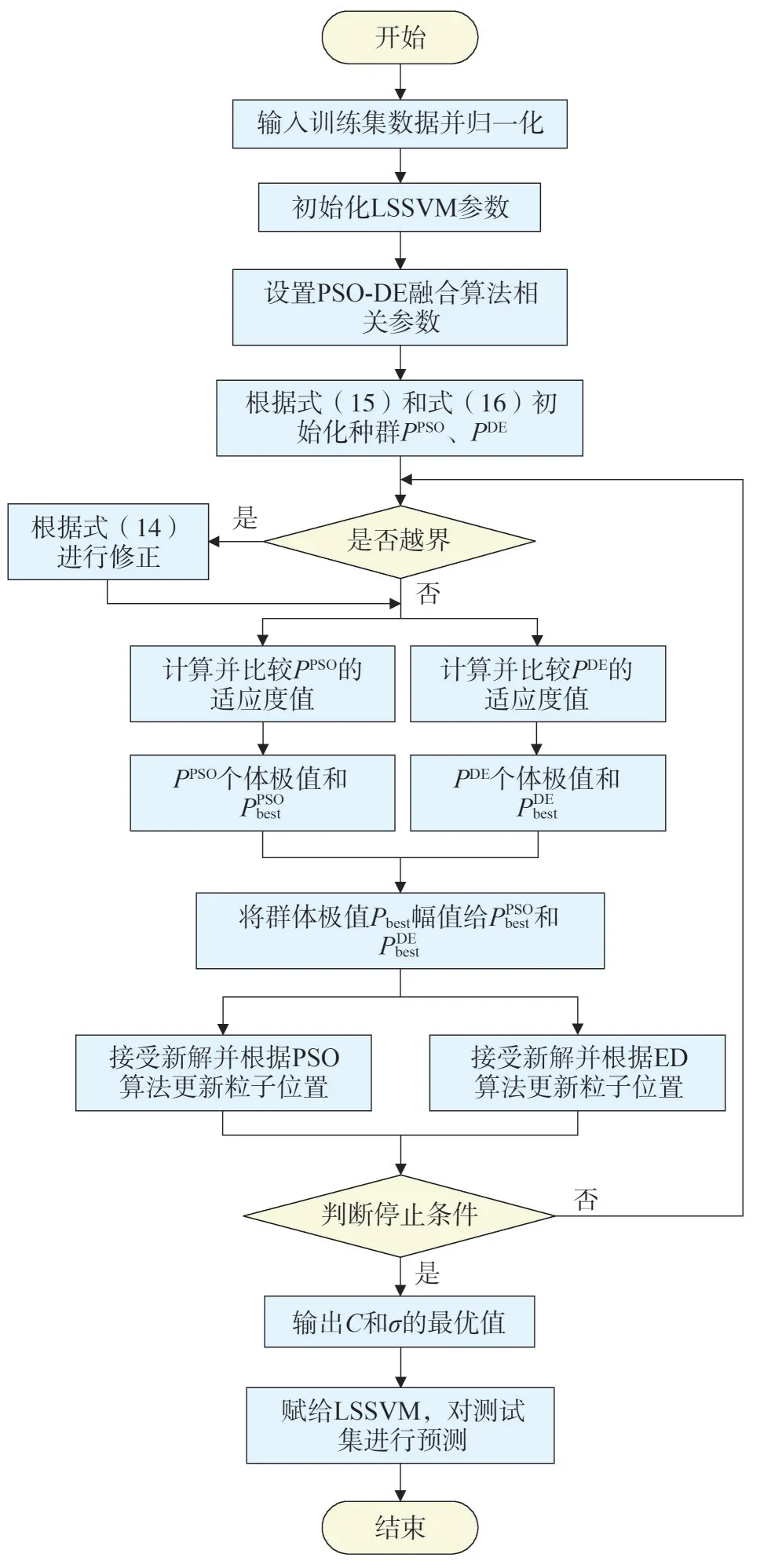
圖1 建模流程

步驟1）將獲取的風功率歷史數據組成樣本數據輸入運算系統中。

步驟2）對風功率歷史數據進行預處理，主要包括刪除錯誤數據和補充缺失數據，缺失數據采用前后兩個數據取平均值的方法予以補充，然后根據需要將預處理后的數據分為訓練集和測試集，并對樣本數據進行歸一化。歸一化的公式為

式中：x′為歸一化后的數據；x為風功率原始值；xmax為風功率最大值；xmin為風功率最小值。

步驟3）初始化LSSVM，并設置相關參數，將C和σ作為尋優目標，設置C和σ的初始值分別為100和1。

步驟4）設置PSO-DE 融合算法相關參數：種群規模為30，最大迭代次數為300，閾值為0.1，慣性權系數初值和終值分別為0.9 和0.4，加速因子為2.05，DE 加權系數、變異算子和變異率分別為0.5、0.8和0.01。

步驟5）設置適應度函數，以訓練樣本的均方根誤差作為PSO-DE融合算法的適應度函數，具體為

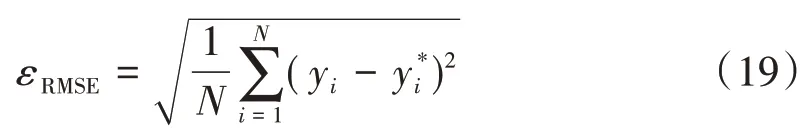
式中：N為樣本容量；yi為第i個風功率的實際值；為第i個風功率的預測值。

步驟6）參數初始化，將種群中的個體分配給種群PPSO和PDE，利用式（15）和式（16）分別為各粒子賦初值。

步驟7）利用PSO 算法更新種群PPSO中各粒子的速度和位置，并利用式（14）對越界的粒子進行修正。同時利用DE 算法對種群PDE中各粒子執行選擇、雜交、變異操作，并利用式（14）對越界的粒子進行修正。

步驟8）找出種群PPSO和PDE中的最優個體A1=和A2=。

步驟9）計算并比較a1=θ(A1)和a2=θ(A2)的大小，選擇適應度值小的個體進入下一代。

步驟10）判斷是否達到目標精度或最大迭代次數，若是，則輸出C和σ的最優值，否則返回。

步驟11）將C和σ最優值賦給LSSVM，對測試集數據進行預測。

2.3 模型的評價

根據《風電功率預測功能規范》［20］，采用平均相對誤差、全局最大相對誤差和均方根誤差對風功率預測模型進行綜合評價評價。均方根誤差計算公式已在式（19）中給出，平均相對誤差和全局最大相對誤差分別為：

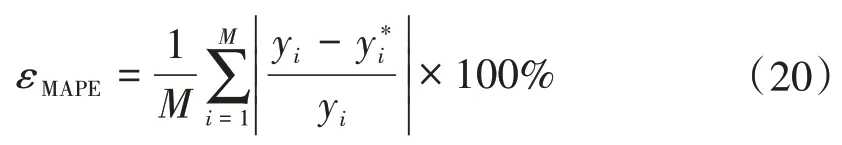
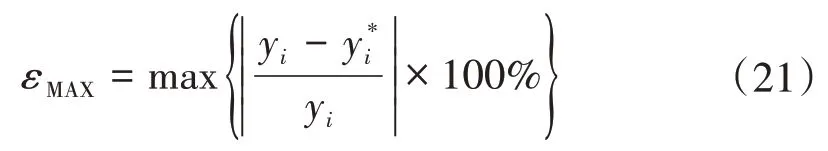
式中：M為測試集的樣本容量。

3 算例分析

本算例仿真數據來源于內蒙古地區某大型風電場，圖2 給出了經預處理后的該風電場3 號風電機組連續6 天輸出功率數據，風功率的采集周期為15 min，共576 組采樣數據。將576 組樣本數據分為兩部分，前132 h 共528 組數據作為訓練集，用于訓練模型，后12 h 共48 組數據作為測試集，用于檢驗模型的精度。

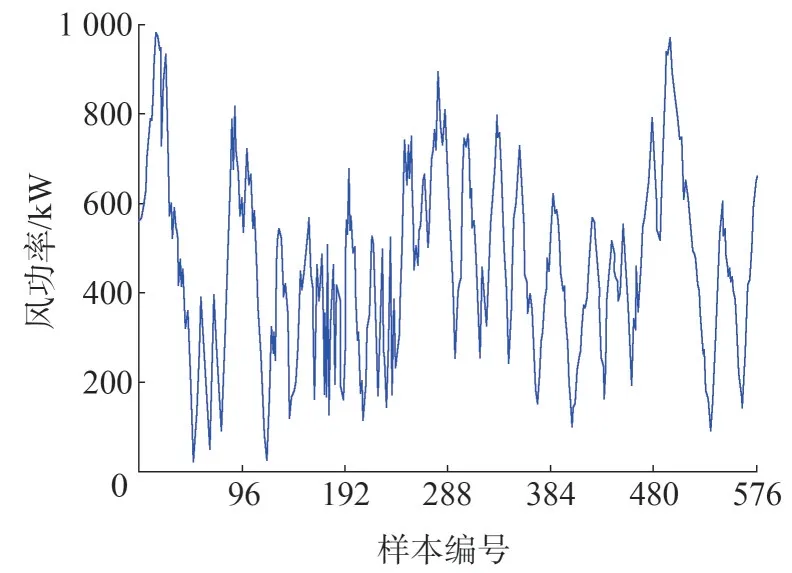
圖2 3號風電機組連續6天輸出功率數據

由于風功率時間序列具有混沌屬性，建立風功率預測模型時，嵌入維數m選擇至關重要，m取值過小，導致數據間的關聯性較弱，回歸效果較差，m取值過大，會大大增加計算量，造成數據冗余，導致誤差變大。因此，首先采用MATLAB 軟件libsvm 工具箱中的自帶參數作為LSSVM 的懲罰因子和核函數，選擇不同嵌入維數（m=1，2，…，8）組成訓練樣本進行訓練，找出用于風功率建模最合理嵌入維數。不同嵌入維數組成訓練集訓練后的平均相對誤差和全局最大誤差如表2所示。

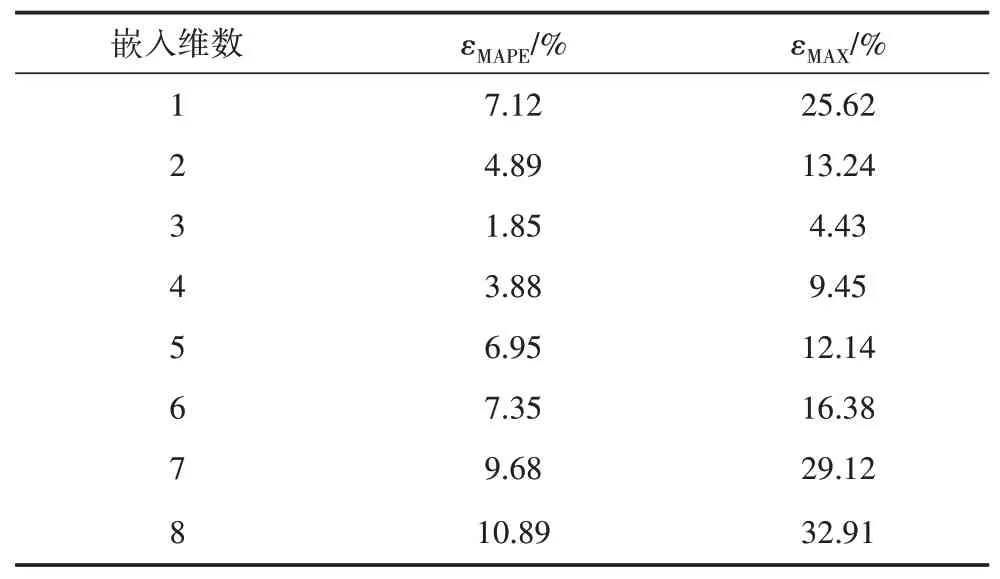
表2 不同嵌入維數組成訓練集訓練誤差

從表2 可知，嵌入維數m從1 到8 變化的過程中，訓練集的平均相對誤差先逐漸減小，當m=3時達到最小為1.85%，然后逐漸增大，全局最大誤差和平均相對誤差變化趨勢基本一致，全局最大誤差也在m=3時達到最小為4.43%。可見建立風功率預測模型時的嵌入維數應選擇m=3。

圖3 給出了嵌入維數m=3 時訓練集樣本的相對誤差，由圖3可知，共有10個樣本相對誤差的絕對值大于3%，其他樣本的相對誤差均在±3%以內，可見本次風功率預測模型的訓練效果較好。

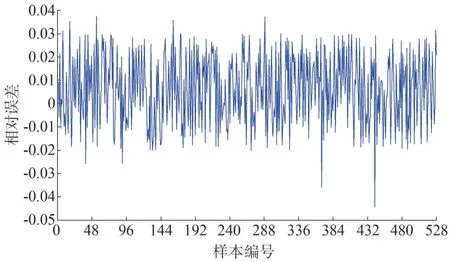
圖3 訓練集相對誤差

利用改進PSO-DE 融合算法對LSSVM 的C和σ進行尋優，改進PSO-DE 融合算法尋優迭代過程如圖4所示。為了對比改進PSO-DE融合算法的優越性，圖4中同時給出了PSO算法、DE算法和PSO-DE 融合算法的迭代曲線，由圖4 可知，改進PSO-DE 融合算法收斂時的迭代次數更少，優化效果更好。

圖4 四種優化方法適應度曲線

表3 給出了四種算法優化結果，由表3 可知，PSO 算法、DE 算法和PSO-DE 融合算法和改進PSODE 融合算法的迭代次數分別為132 次、158 次、62 次和34 次，由此可見，改進PSO-DE 融合算法能夠充分發揮PSO 算法和DE 算法的優勢，有效減少算法迭代次數，提高計算精度，同時也驗證了所提PSO-DE 融合算法改進策略的正確性。

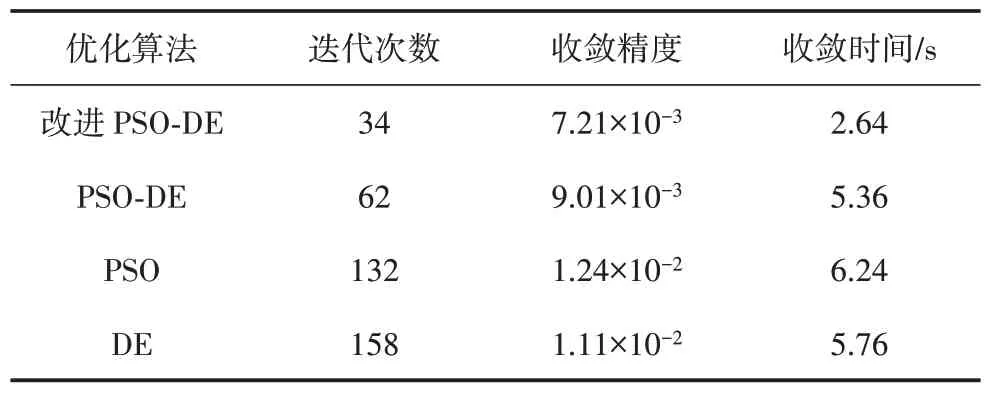
表3 四種算法優化結果對比

將C和σ的最優值賦給LSSVM 對測試集數據進行外推預測，預測結果如圖5所示，由圖5可知，基于改進PSO-DE 融合算法優化LSSVM 的風功率預測模型的預測效果較好，風功率預測結果與實際功率的變化趨勢基本一致。

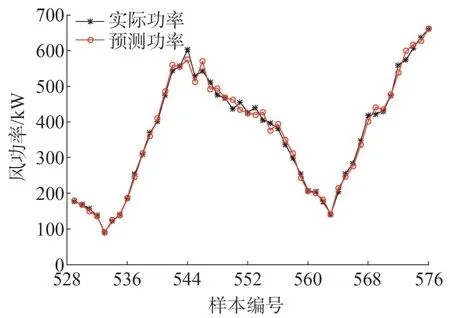
圖5 測試集風速預測結果

測試集數據預測的相對誤差如圖6 所示，由圖6可知，本次功率預測相對誤差范圍均在±6%的范圍內，共有4 組樣本相對誤差絕對值超過5%，剩余44組樣本相對誤差均在±5%以內，最大相對誤差為5.97%，占測試集樣本總量的91.67%，可見本次預測誤差控制較好。

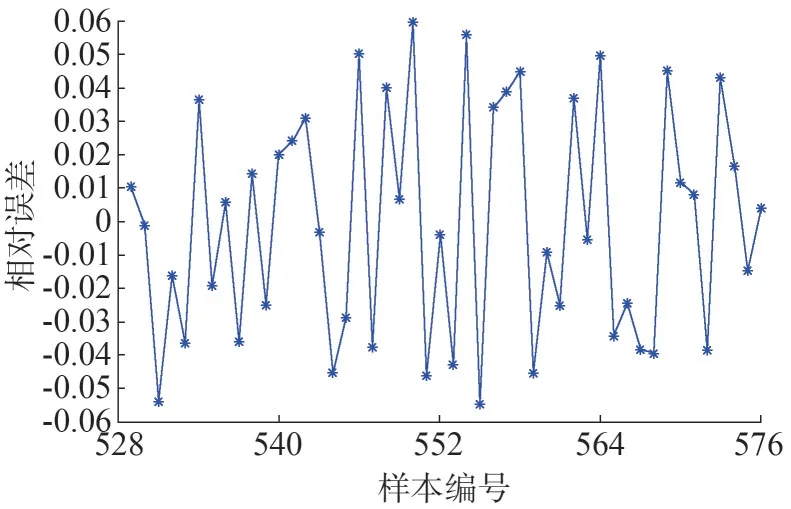
圖6 測試集預測結果相對誤差

為了驗證風功率預測方法的實用性，采用相同風電功率數據分別建立粒子群算法優化最小二乘支持向量機（PSO-LSSVM）、粒子群算法優化極限學習機（PSO-ELM）、遺傳算法優化BP 神經網絡（GA-BP）3 種風功率預測模型，利用訓練集進行訓練，測試集檢驗各模型的精度，并與基于改進PSO-DE 融合算法優化LSSVM 的短期風功率預測模型的計算結果進行對比，4 種風功率預測模型的平均相對誤差、均方根誤差和全局最大誤差計算結果如表4所示。

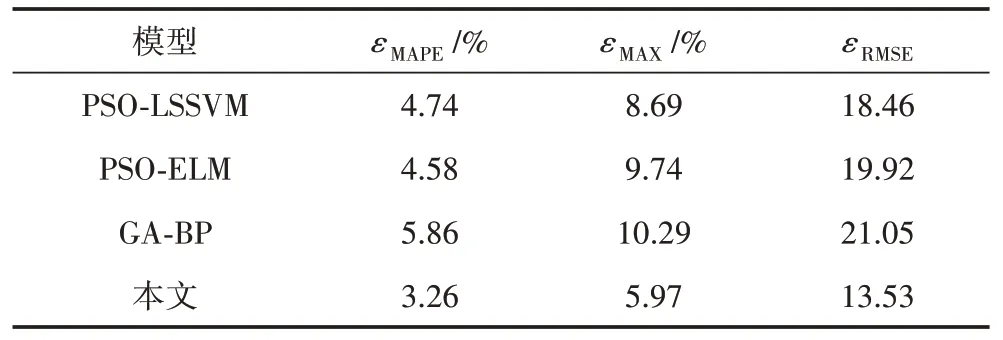
表4 3種風速預測模型誤差

從表4 可以看出，在平均相對誤差方面，本文模型的平均相對誤差最小，僅為3.26%，相比于PSOLSSVM 模型下降31.22%，誤差控制效果顯著；在全局最大誤差方面，本文模型為5.97%，小于其他3 種模型，可見模型外推預測的波動性較小；在均方根誤差方面，本文模型的均方根誤差為13.53，相比于PSO-LSSVM 模型下降26.71%，可見模型外推預測穩定性更好。綜上所述，基于改進PSO-DE 融合算法優化LSSVM 的短期風功率預測模型能夠有效減小數據波動，提高計算精度。

4 結語

采用慣性權系數、粒子初始化規則調整和越界粒子變異操作等策略對PSO-DE 融合算法進行改進，仿真分析表明，改進PSO-DE 融合算法找到最優解的迭代次數更少，收斂效果更好，有效減少了算法的迭代尋優次數，提高了算法的收斂性能。

采用改進PSO-DE 融合算法對LSSVM 的懲罰因子和核函數參數進行優化，建立了基于改進PSO-DE融合算法優化LSSVM 的風功率預測模型，采用風電場實際運行數據進行算例分析，結果表明，基于改進PSO-DE 融合算法優化LSSVM 的風功率預測模型的平均相對誤差、全局最大誤差和均方根誤差分別為3.26%、5.97%和13.53，預測效果好于對比的其他模型，驗證了提出的改進策略及短期風功率預測模型的正確性。