儲能逆變器H∞魯棒跟蹤控制

于 芃，孫樹敏，程 艷，王士柏，王玥嬌

（國網山東省電力公司電力科學研究院，山東 濟南 250003）

0 引言

近年來，在我國電力系統(tǒng)中，以光伏風能等為代表的新能源發(fā)電裝機增長猛烈，因此須對電網供電臺區(qū)中儲能系統(tǒng)、電動充電樁以及用戶可移動負荷等對象進行協(xié)同控制［1］。同時，由于各類儲能裝置輸出為直流電，需要電力電子器件的逆變才可滿足在臺區(qū)的穩(wěn)定運行或并入交流大電網。由于供電臺區(qū)結構及運行方式復雜，逆變器需具有多種控制策略才能滿足電壓、頻率各項指標的平穩(wěn)運行。幾種控制策略中，功率控制模式控制中分布式電源一般無法給供電臺區(qū)系統(tǒng)提供可靠的電壓支撐，電壓頻率控制模式控制外特性較差，一般在孤島狀態(tài)下工作［2-3］。

國內外學者提出了基于下垂控制的虛擬同步發(fā)電技術控制策略［4］，通過下垂控制模擬傳統(tǒng)同步發(fā)電機靜態(tài)特性，使得各儲能單元輸出功率實現(xiàn)合理分配，模擬了同步發(fā)電機的機械方程，使電網具有慣性和阻尼。文獻［5］提出了一種考慮線路阻抗效應的分布式交流電力系統(tǒng)并聯(lián)逆變器控制，不需要控制互連，并自動補償逆變器參數變化和線路阻抗不平衡。文獻［6］在基于逆變器輸出阻抗的基礎上，進行了電壓電流多環(huán)反饋控制器的設計，但該方法只能用于理想情況下輸出阻抗為感性時。

在電力系統(tǒng)中，各類電力裝置負荷時間常數不同，響應不同。當擾動發(fā)生時，系統(tǒng)同時存在微秒級別震蕩的電磁暫態(tài)過程，亦存在毫秒級別快速變化的機電暫態(tài)響應。這就導致了系統(tǒng)抗擾動能力較弱［7-8］。文獻［9］提出了一種相位超前補償的方法來補償電感電流反饋的延時，分析了不同諧振頻率下系統(tǒng)的響應。此時，傳統(tǒng)下垂策略中基于坐標系解耦的比例-積分控制策略以及自適應調節(jié)無法應對系統(tǒng)擾動的快速變化。運用現(xiàn)代魯棒控制理論，當系統(tǒng)存在外界較大擾動或參數攝動時，基于系統(tǒng)模型可以設計出具有良好抗擾效果的魯棒控制器［10-11］。

文獻［12］構建了一種混合靈敏度函數，用以提高微電網抗擊直流和交流擾動的能力，文獻［13-14］提出了一種基于混合靈敏度來控制交直流混合微網系統(tǒng)中頻率的控制策略，構建回路靈敏度函數，利用線性矩陣不等式求解Riccati 方程得到頻率控制器，增強了頻率對參數攝動的魯棒性。

在現(xiàn)有研究的基礎上，提出了一種用于儲能逆變器虛擬同步發(fā)電機（Virtual Synchronous Generator，VSG）控制中對電壓H∞魯棒控制方法，解決了負載突變與濾波器參數變化降低電壓質量的問題。相較于常規(guī)的電壓電流雙閉環(huán)比例-積分控制或下垂控制，跟蹤系統(tǒng)電壓能力、抗干擾能力更強。首先在傳統(tǒng)VSG控制合成參考電壓后，建立系統(tǒng)結構的機理模型，同時對掃頻輸入到正弦波脈寬調制調制器產生的逆變器輸出信號進行采集辨識得到系統(tǒng)的辨識模型，二者比較后，將外界干擾和建模誤差作為不確定性函數建立H∞魯棒控制器對參考電壓進行跟蹤，增加了系統(tǒng)抗干擾性能，并通過MATLAB/Simulink搭建逆變器閉環(huán)控制模型，驗證了所提出控制策略的有效性。

1 儲能逆變器主電路系統(tǒng)設計

1.1 虛擬同步發(fā)電技術原理

虛擬同步發(fā)電機中的下垂控制即模擬同步發(fā)電機有功功率與頻率的關系（功頻特性）和無功功率與電壓的關系（勵磁特性）。圖1 所示為儲能逆變器下垂特性曲線，包括功頻特性曲線和勵磁特性曲線。

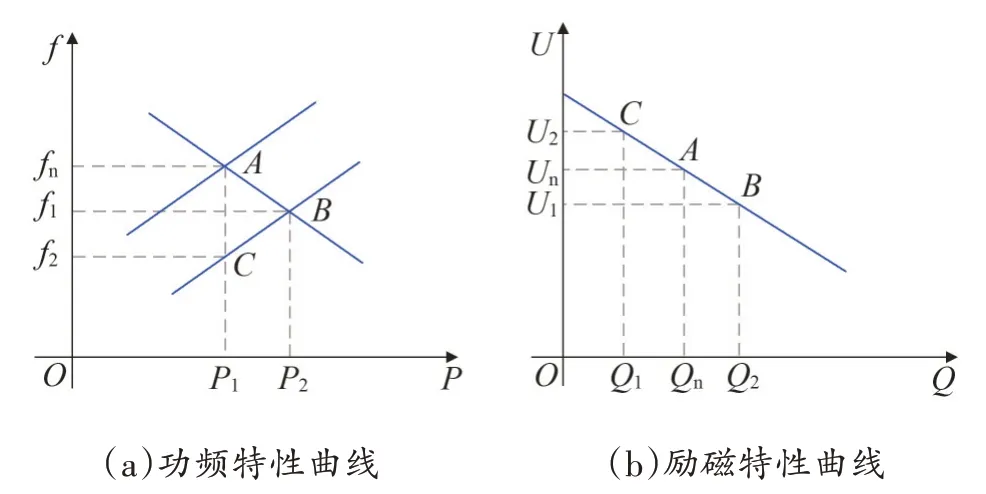
圖1 下垂特性曲線

由圖1 可以推出，由逆變器功率下垂特性可以推出，傳統(tǒng)的下垂控制數學表達式為：

式中：fn為電網額定頻率，一般為50 Hz；Un為電網參考電壓幅值；f、U為下垂控制器輸出參考值；M、N分別為有功、無功下垂系數；Pref、Qref為額定參考功率。

虛擬同步發(fā)電技術在下垂調節(jié)有功-頻率環(huán)中模擬了同步發(fā)電機的機械特性，即

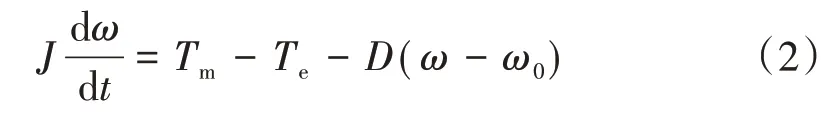
式中：J為同步發(fā)電機轉動慣量；Tm為機械轉矩；Te為電磁轉矩；D為阻尼系數；ω0為電網額定角速度；ω為實際輸出電壓角速度。

儲能逆變器中引入轉動慣量和阻尼使系統(tǒng)的頻率支撐更可靠，對頻率震蕩有較強抑制作用，能夠更快過渡暫態(tài)過程［15］，同時又可以不受同步發(fā)電機中定子和轉子等物理結構的限制，具有更寬的運行范圍和動態(tài)性能。

1.2 儲能逆變器主電路結構

在供電臺區(qū)中，多個分布式電源或儲能系統(tǒng)經逆變器等電力電子裝置高質量地向各類負荷供電，經過繼電器、變壓器等配電裝置與配電網絡相連接。在本文中，將其中一個分布式電源構成的局域臺區(qū)用逆變器控制電路進行等效研究，假設直流側電壓源Udc為常數，維持不變。

基于電壓魯棒控制的儲能逆變器原理如圖2 所示，主要包括：直流電源代替分布式電源提供直流電；三相電壓源逆變器將直流電轉為三相交流電；電感-電容濾波電路將逆變器輸出的方波轉化為符合電能質量要求的三相正弦波以及控制器部分，控制器部分包括VSG 調節(jié)環(huán)節(jié)，電壓合成環(huán)節(jié)和魯棒控制器。

根據直流側電源性質的不同，逆變電路可分為兩種形式：電流源型逆變器和電壓源型逆變器，本文主要采用三相全橋電壓源型逆變器。

圖2 中，Udc為直流側電壓；S1—S6為逆變器開關管；L、C分別為濾波器的濾波電感、電容，為避免電感-電容濾波器震蕩，在電容處并聯(lián)一個小電阻R；ea、eb、ec為逆變器輸出相電壓；iLa、iLb、iLc為VSG 輸出電感電流；Uabc為VSG 輸出電容電壓；Iabc為逆變器輸出電流；為VSG算法輸出參考電壓。

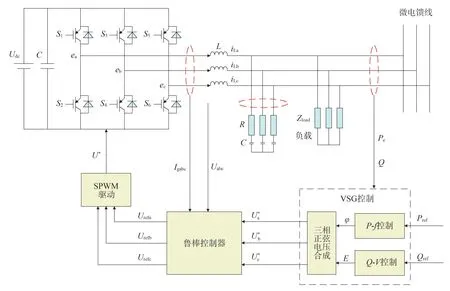
圖2 系統(tǒng)整體控制原理

利用電壓電流傳感器采集到的輸出電壓Uabc和輸出電流Iabc，在三相靜止坐標系計算得到瞬時有功功率P和瞬時無功功率Q后轉為dq坐標系下的功率關系式分別為：

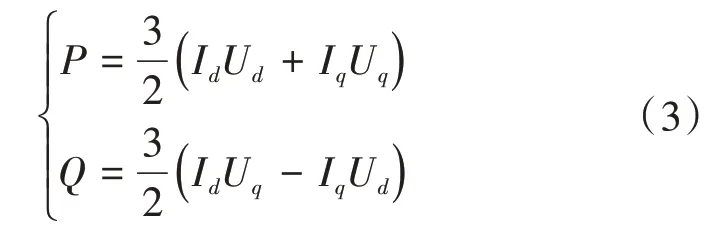
式中：Ud、Uq為dq坐標系下的輸出電壓；Id、Iq為dq坐標系下的輸出電壓［16］。

綜上所述，可以得到基于H∞魯棒控制的儲能下垂逆變器的基本流程為：傳感器采集輸出電流Iabc和電壓Uabc，經過功率計算得到輸出瞬時功率，加入后低通濾波器得到平均有功功率和無功功率。通過VSG 控制環(huán)節(jié)得到頻率指令值和電壓幅值參考值，對頻率對應的角速度進行積分得到電壓相位角，由此合成了三相對稱的參考電壓Uref，經過park 變換從三相坐標系轉為dq坐標系后，將其輸入到魯棒控制模塊中得到參考信號，再經過正弦脈寬調制技術（Sinusoidal Pulse Width Modulation，SPWM）得到脈沖驅動信號控制逆變器中開關管的通斷，從而控制逆變單元的輸出電壓。

1.3 系統(tǒng)數學模型的建立

在電力系統(tǒng)中，儲能單元、逆變器、濾波器等環(huán)節(jié)本身包含了大量非線性元件，如二極管、開關管等。所以整個系統(tǒng)本質上可以當作一個非線性且離散的系統(tǒng)。工程上常采用平均開關模型法來得到系統(tǒng)的數學模型，其原理是將一個開關周期內的瞬時值用平均值代替。

根據基爾霍夫定律，建立逆變器在三相靜止坐標系下的數學模型，表達式為：

式中：Ua、Ub、Uc為逆變器輸出電容電壓；Ia、Ib、Ic為負載公共連接點的電流。

實際工程應用中，由于SPWM 控制逆變器開關管其狀態(tài)不連續(xù)，假設開關器件的頻率遠大于基波輸出電壓的頻率，我們常使用狀態(tài)空間平均模型法得到逆變電路控制模型。

假設逆變器帶三相對稱阻性負載，則由式（4）可推得逆變橋輸出電壓UkN與公共連接點電壓即負載電壓Uk的傳遞函數為

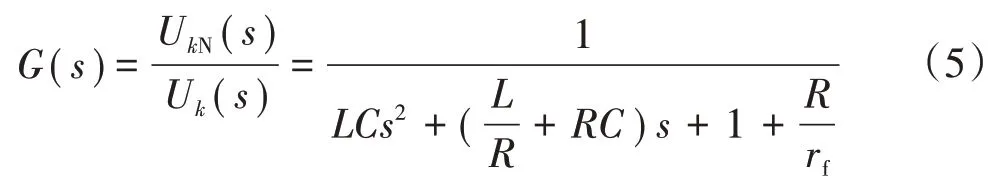
式中：rf為負載電阻。

對于SPWM 調制的三相逆變器，當考慮主電路的延時，逆變器則可當作一個滯后環(huán)節(jié)，忽略高次項，其簡化后的滯后環(huán)節(jié)傳遞函數為

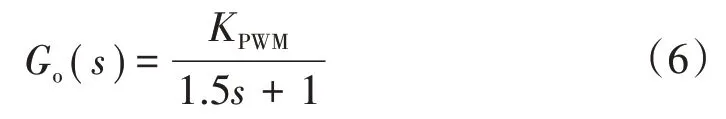
式中：KPWM為逆變器比例系數。根據SPWM 調制原理，當載波信號頻率fc遠大于調制波信號頻率f時有

式中：Ulm為逆變橋輸出基波幅值；mlm為調制比。

由式（5）—式（7）可推得逆變電路從SPWM 調制器輸入到輸出負載電壓的傳遞函數為

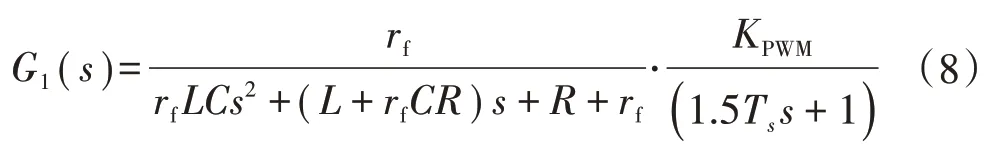
以上分析均是基于系統(tǒng)結構建立的機理模型。然而，由于系統(tǒng)的建模誤差，以及各環(huán)節(jié)存在的參數不確定性如有功功率和無功功率的耦合，進而導致數學模型推算復雜。故本文采取了基于系統(tǒng)運行和實驗數據辨識得到的模型。

為了對電壓源逆變器組成的逆變電路的動態(tài)性能進行分析和控制，首先要得到逆變電路的動態(tài)特性的數學模型，以三路掃頻信號作為SPWM 的調制信號，對電壓源逆變器進行充分的激勵，從而得到相應的頻率響應，根據頻率響應辨識可得逆變電路的數學模型。

以三路掃頻信號作為SPWM 的調制信號，采集逆變器經過濾波器后輸出的一路電容電壓如圖3所示。

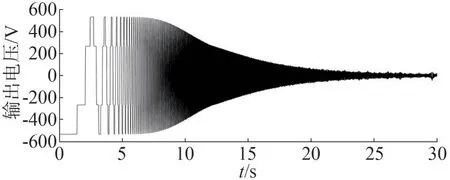
圖3 輸出響應曲線

由于開始輸入掃頻信號的頻率很小，遠小于濾波器的截止頻率，故輸出電壓波形開始時依舊為方波，隨著頻率的上升逐漸變?yōu)檎也ǎ?7］。

將采集到的時域中的輸入輸出電壓信號通過離散傅里葉變換輸入到頻域中，并根據頻譜關系畫出該系統(tǒng)的波特圖。

利用離散傅里葉變換后的輸入輸出數據通過MATLAB 中的系統(tǒng)辨識工具箱辨識得到的從SPWM調制器輸入端的調制電壓到逆變器輸出電壓的傳遞函數為

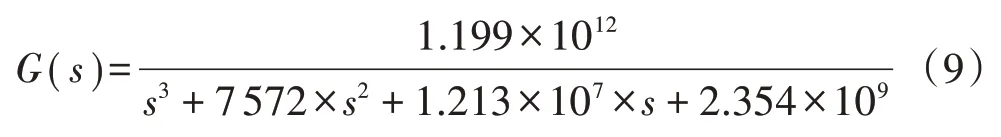
從圖4 中可以看出，辨識所得的傳遞函數可以較好地擬合電壓源逆變器組成的逆變電路的頻率特性曲線。

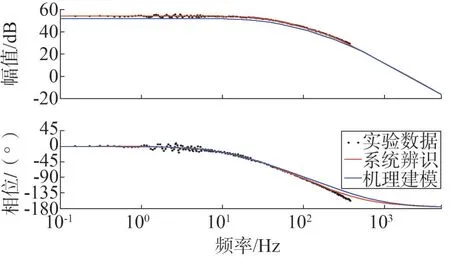
圖4 模型辨識曲線

2 逆變器電壓魯棒控制器的設計

當儲能系統(tǒng)長期運行時，其系統(tǒng)參數如濾波器參數會發(fā)生變化，使得供電質量下降。魯棒控制器是基于能反應系統(tǒng)的真實物理特性的傳遞函數族P 來進行設計的。它不僅能粗略表示系統(tǒng)物理特性的標稱模型G，即上一章節(jié)中通過辨識得到的傳遞函數；還會考慮系統(tǒng)的不確定性即系統(tǒng)受外界干擾以及參數變化等因素引起的擾動，二者組成一個廣義被控對象，如圖5 所示。其中，Δm為規(guī)范化不確定性加性攝動，并且‖Δm‖≤1；Wm為加性不確定性加權函數；r和y分別為輸入輸出。

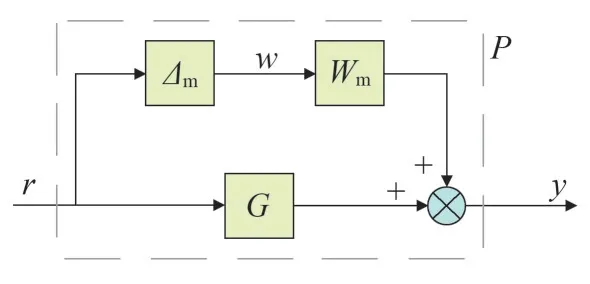
圖5 廣義被控對象

魯棒控制器的設計可以使廣義被控對象達到穩(wěn)定，并且具有較好的跟蹤性能［18］。其控制思想的核心是最小化干擾對輸出的影響。

2.1 模型的不確定性

由式（9）中的傳遞函數以及圖5 的模型辨識曲線可以看出，系統(tǒng)的真實物理特性在標稱模型上下波動，這是由于受參數攝動、傳感器靈敏度以及電力系統(tǒng)的擾動誤差等影響，通過正弦掃頻信號激勵儲能逆變器辨識得到的標稱模型不能完全描述系統(tǒng)真實的物理特性。因此，將儲能逆變電路的外界干擾和建模誤差看作模型的不確定性，則儲能逆變器的真實模型可以描述為

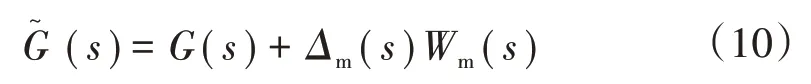
通過實驗確定逆變器工作系統(tǒng)的標稱模型G(s)與實際系統(tǒng)在頻率不同時的最大相對誤差，系統(tǒng)工作原理如圖6所示。在1～100 Hz的頻率范圍內選擇多個頻率的激勵信號rx，對逆變電路進行激勵，得到穩(wěn)態(tài)誤差的最大值ex。通過多次實驗，測得標稱系統(tǒng)在期望頻率范圍內的加性不確定性上界如圖7所示。

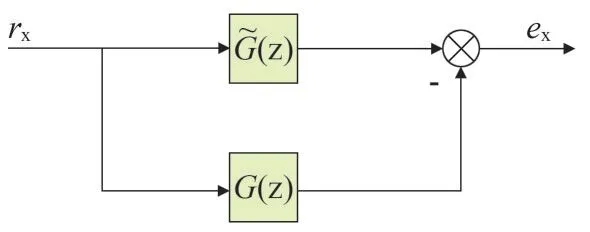
圖6 系統(tǒng)工作原理

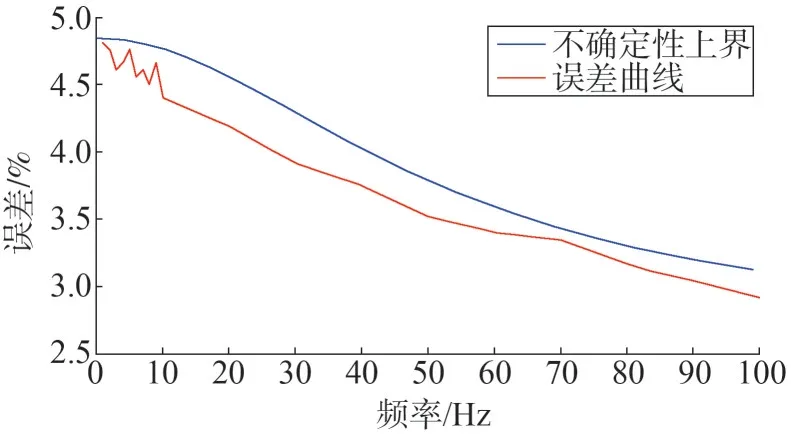
圖7 加性不確定性

通過對最大誤差進行估計，可以得到G(s)的一個一階不確定性上界Wm(s)如下所示。

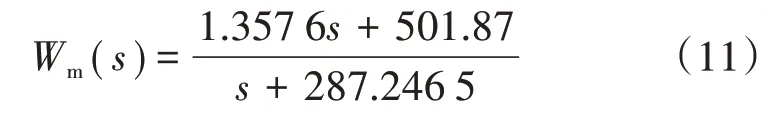
經過上述工作求得系統(tǒng)的不確定性之后，按圖8所示進行線性分式變換（Linear Fraction Transformation，LFT），其中輸入為Z=[r u w]T，輸出W=[y zwe]T，可以求得廣義被控對象P為

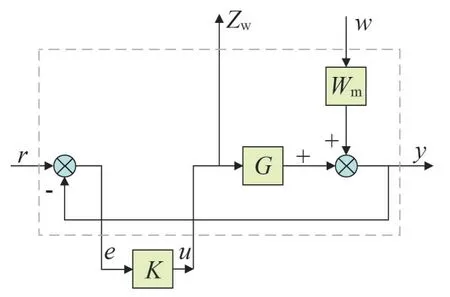
圖8 LFT變換

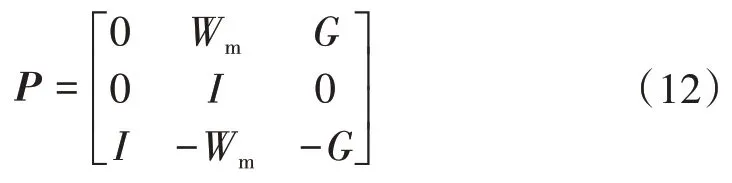
控制系統(tǒng)如圖9所示，其中w是模型不確定性的輸入，r為期望值即參考輸入。

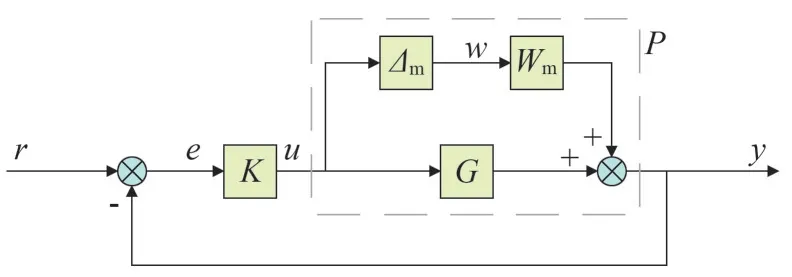
圖9 控制系統(tǒng)

經過上述LFT 變換，儲能逆變器輸出電壓的控制問題就轉化為標準的H∞魯棒控制問題［19］。

2.2 H∞魯棒控制器設計

H∞魯棒控制器的作用是當系統(tǒng)不確定性Δm(s)和外部干擾噪聲存在的時候，保證系統(tǒng)仍然能夠穩(wěn)定地運行，使系統(tǒng)的輸出能夠跟蹤期望輸入，并且能夠增強整個系統(tǒng)的抗干擾的性能，從而使儲能系統(tǒng)可以對電網進行高可靠供電。H∞魯棒控制系統(tǒng)的系統(tǒng)如圖9 所示。其中，r為期望值即參考輸入電壓udqref，y為輸出即母線電壓udq，G為建模得到的供電臺區(qū)儲能逆變器的標稱模型，Wm(s)為上面小節(jié)中通過實驗確定的模型加性不確定性上界，Δm(s)是規(guī)范化加性不確定性，K為待設計的魯棒控制器，u為控制器的輸出，e為期望值與實際值的誤差。

這樣，逆變器的輸出電壓的控制問題就可以變換為標準的H∞控制問題。標準的H∞控制框圖如圖10 所示，其中輸入為r=[udqref，Z]T；輸出為y=[udq，W]T，P為廣義被控對象，如圖9 所示的虛線框內所示；K為待設計的魯棒控制器。

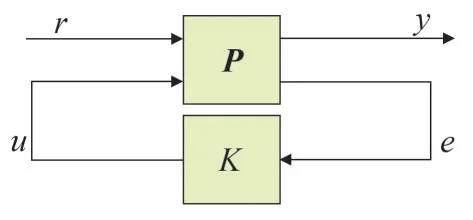
圖10 標準的H∞控制

于是有

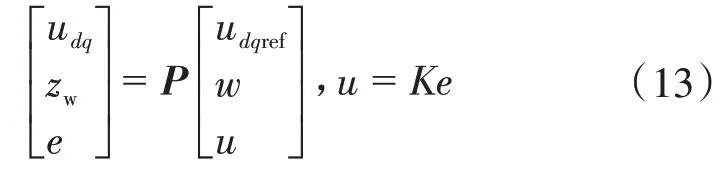
式中：zw為控制器的不確定性。因此，為保證供電臺區(qū)系統(tǒng)的魯棒穩(wěn)定性，并抑制Z對輸出的影響，要解決的抗干擾問題轉化為設計一個輸出反饋控制器K，使臺區(qū)中的逆變器輸出電壓閉環(huán)系統(tǒng)穩(wěn)定，并且使Pzω的H∞范數最小，即

根據標準的H∞魯棒控制器解法，并利用MATLAB 中的Hinfsyn 函數進行控制器的求解，得到四階魯棒控制器為

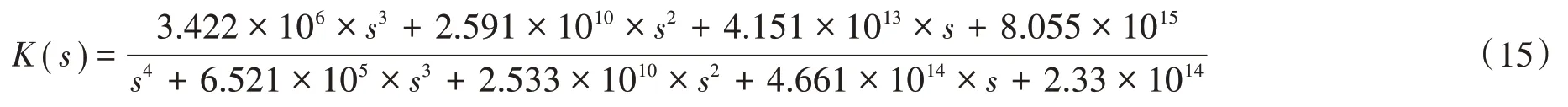
對加控制器的閉環(huán)系統(tǒng)進行頻域分析，得到閉環(huán)系統(tǒng)的波特圖［20］，并與開環(huán)系統(tǒng)的波特圖做比較，如圖11 所示。圖11 中G為開環(huán)傳遞函數，GC為閉環(huán)傳遞函數。

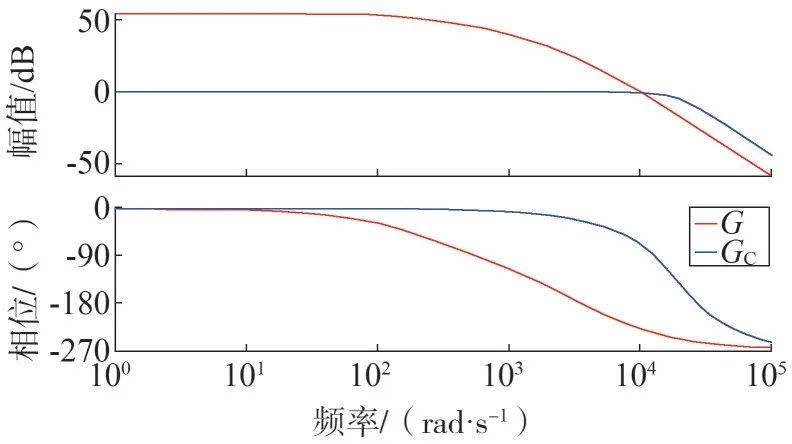
圖11 系統(tǒng)開環(huán)與閉環(huán)波特圖對比

3 仿真驗證

為驗證所提出的基于魯棒控制的儲能逆變器控制策略的可行性和正確性，在MATLAB/Simulink 仿真平臺中，根據圖1 中系統(tǒng)的基本結構框圖搭建了電壓源型逆變器下垂系統(tǒng)模型，仿真參數如表1 所示。儲能逆變器始終工作在孤島狀態(tài)，帶三相阻性負載，通過仿真驗證系統(tǒng)在突加或突減負載的情況下，系統(tǒng)的輸出電壓輸出頻率及輸出功率的變化，驗證儲能系統(tǒng)對電網調峰的需求，同時觀察系統(tǒng)參數變化時，電壓電流諧波含量相較于傳統(tǒng)控制策略的提升，滿足其調峰調壓調頻一體化要求。

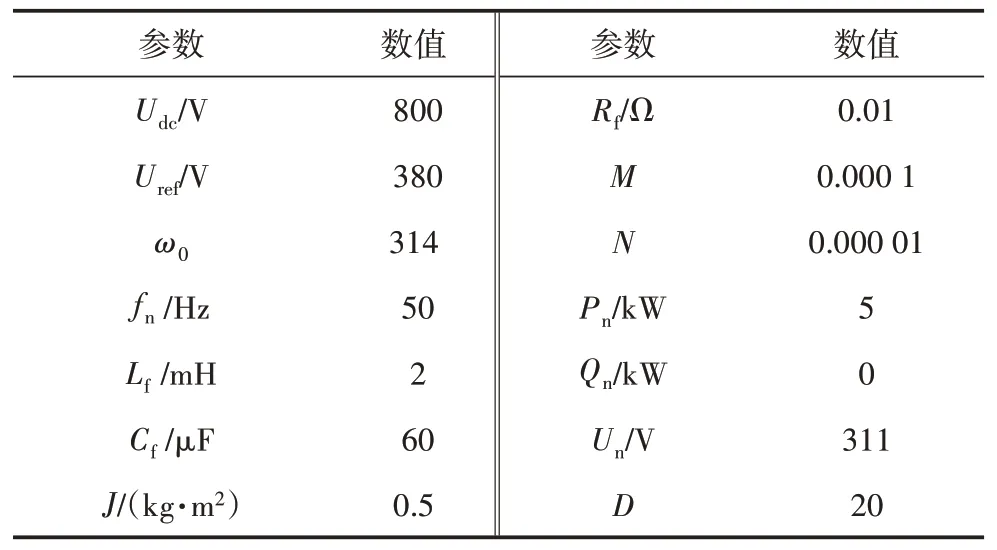
表1 系統(tǒng)仿真參數

本文的控制算法主要對系統(tǒng)輸出的三相電壓和頻率進行控制，為了簡化模型以突出對逆變器控制問題的突出討論。

3.1 負載投切工況對比

設置仿真時間為1.2 s，最初系統(tǒng)處于單機孤島運行狀態(tài)，帶一個有功功率為5 kW（380 V/50 Hz），無功功率為2 kvar（380 V/50 Hz）的三相對稱阻性負載，在0.4 s 時，系統(tǒng)突加一個有功功率2 kW，無功功率為2 kvar 的阻性負載，在0.8 s 時突減該負載。利用不同負載的投切模擬負載突變的情況。觀察系統(tǒng)的動態(tài)響應的暫態(tài)過程。整個過程，系統(tǒng)輸出的電壓波形和電流波形如圖12和圖13所示。

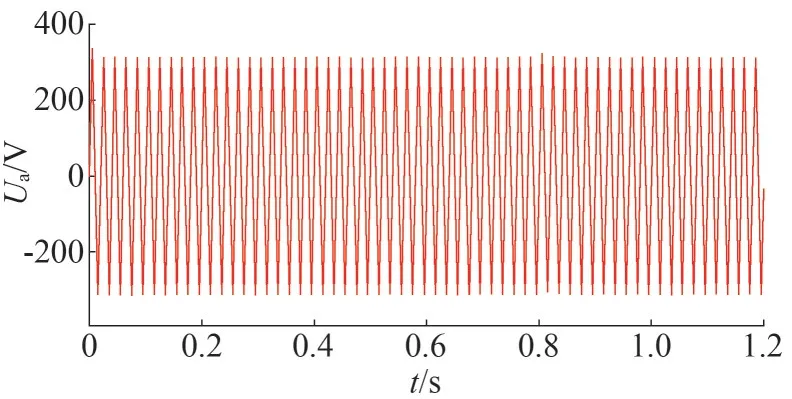
圖12 逆變器輸出電壓波形

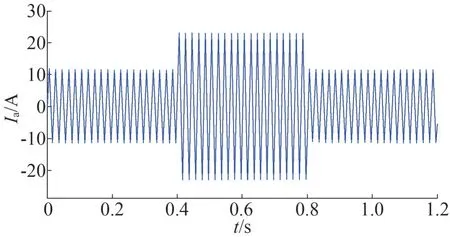
圖13 逆變器輸出電流波形

由圖12 可以看出，當負荷變化時，輸出電壓開始時經過小幅震蕩的暫態(tài)過程后，進入穩(wěn)態(tài)輸出波形無明顯大幅變化。由此可以驗證所選的加權不確定性函數對應的魯棒控制器具有較好的電壓波動抑制能力。圖13 中可以看出輸出電流的大小隨著負載的變化而變化，暫態(tài)響應時間短，且在負載變化時可以快速達到相應狀態(tài)。從而可以看出此控制方法具有良好的跟蹤特性。

采取傳統(tǒng)VSG 控制策略與采用的魯棒控制策略后系統(tǒng)輸出的有功功率對比，如圖14所示。兩種控制策略下系統(tǒng)輸出電壓的頻率變化如圖15所示。

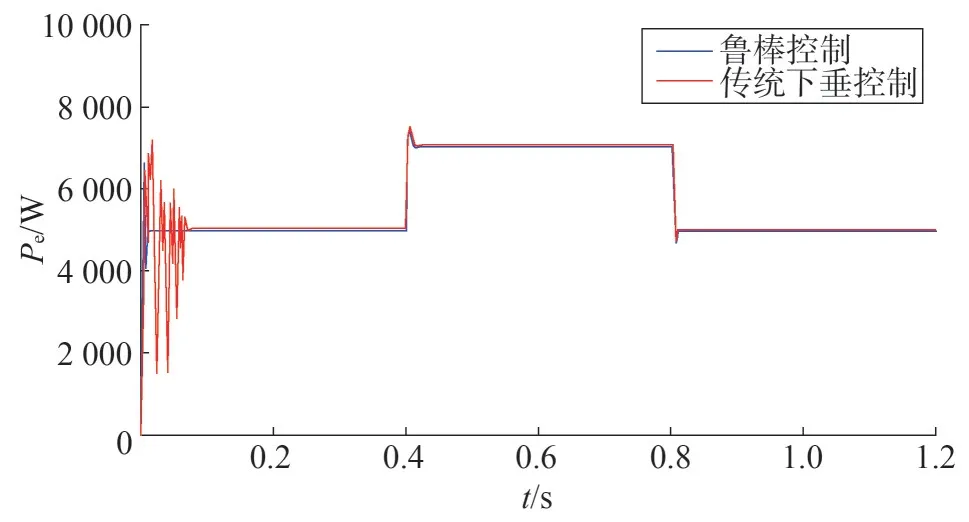
圖14 不同控制策略的輸出有功功率

由圖14 可以看出，傳統(tǒng)控制策略在剛開始接入負荷時，震蕩較明顯，超調量過大，且當負荷突變時，輸出的有功功率也瞬時突變。而采用魯棒控制器的輸出為較平滑的曲線，且在負荷變化時幾乎無超調。由圖15 可以明顯看出，采用傳統(tǒng)控制策略的頻率變化幅度更大，魯棒控制器可以恢復由負荷變動引起的頻率變化。

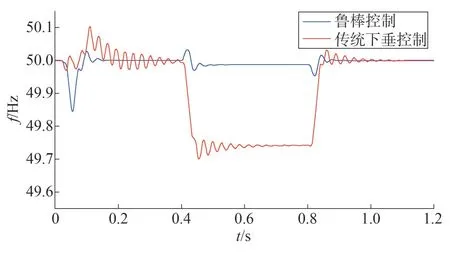
圖15 不同控制策略的頻率

3.2 參數變化工況對比

在仿真模型中，濾波器的電感和電阻中加入白噪聲，模擬參數在一定范圍內的無規(guī)律變化，分析系統(tǒng)輸出的跟蹤和適應能力，結果如圖16—圖19所示。

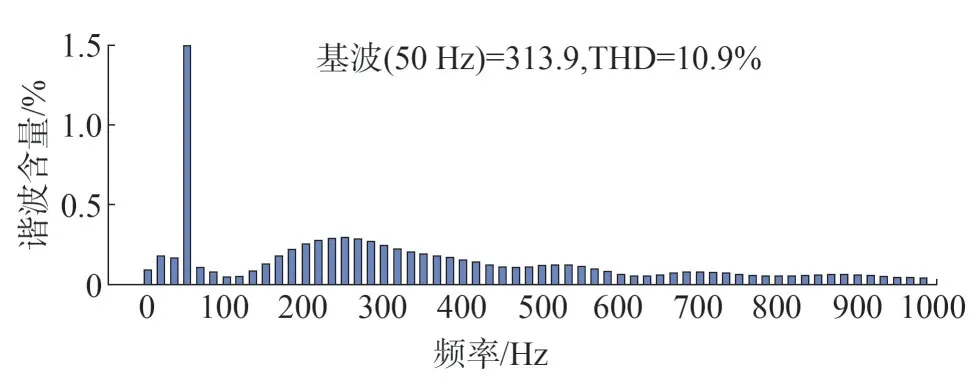
圖16 參數固定時傳統(tǒng)控制電壓諧波分析

圖17 參數固定時魯棒控制電壓諧波分析

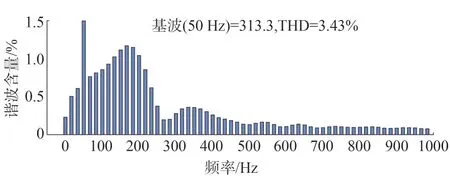
圖18 參數變化時傳統(tǒng)控制電壓諧波分析

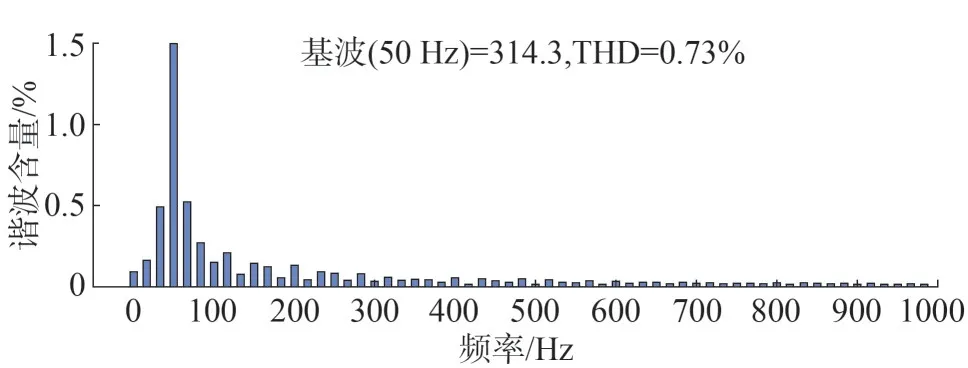
圖19 參數變化時傳統(tǒng)控制電壓諧波分析

由圖16 和圖17 中兩種控制方式電壓諧波分析可知，魯棒控制策略的三相電壓諧波含量（Total Harmonic Distortion，THD）為0.26%，傳統(tǒng)下垂控制策略的電壓諧波含量1.09%，傳統(tǒng)下垂控制雖在標準范圍內，但電能質量較魯棒控制相比明顯下滑。但當參數出現(xiàn)變化時，如圖18 和圖19 所示，傳統(tǒng)下垂控制的電壓諧波含量突增至3.43%，電能質量明顯下滑，采用本文所述的魯棒控制策略的電壓諧波含量僅增加了0.47%，電能質量得到明顯改善，由此可見其可以良好跟蹤系統(tǒng)輸入的特性。

4 結語

在電力系統(tǒng)中，一個供電臺區(qū)具有多元用戶對象，虛擬同步發(fā)電技術中的下垂策略作為儲能逆變器常用的控制策略，其控制策略的好壞決定了分布式電源接入供電臺區(qū)的穩(wěn)定性。傳統(tǒng)VSG 控制是在理想狀態(tài)下線路阻抗呈感性時得到的理想模型，實際控制中必然存在線路損耗與外界干擾。本文在下垂控制策略的基礎上，根據系統(tǒng)運行的輸入電壓與輸出電壓的實驗數據辨識得到系統(tǒng)的數學模型，加入H∞魯棒控制器以改進由傳統(tǒng)VSG 控制引起的電壓跌落，同時使系統(tǒng)頻率偏移量減小，根據系統(tǒng)干擾和誤差建立的不確定性加權函數，可以有效跟蹤系統(tǒng)輸入，提高系統(tǒng)抗干擾能力，從而滿足儲能系統(tǒng)有效參與電網削峰填谷、調頻調壓等功能中。