基于EMD-ARIMA組合模型的長江航運干散貨運價指數預測

楊銀花 金 雁 汪 敏* 張矢宇

(武漢理工大學船海與能源動力工程學院1) 武漢 430063) (武漢理工大學交通與物流工程學院2) 武漢 430063)

0 引 言

長江航運干散貨運價指數(Yangtze River bulk freight index，YBFI)是用來反映我國內河干散貨運輸市場貨運水平變動情況的重要航運經濟指標.由于內河干散貨市場的動態性和不穩定性都與沿海干散貨市場有較大差異，例如，內河運價指數樣本數據點少、周期性不明顯且比沿海相關指數更容易受到外界因素的干擾等，沿海干散貨相關預測分析方法不適用.現階段對內河航運干散貨運輸市場波動分析及預測的研究較少，國內外學者主要對中國沿海散貨運輸市場的CBFI、國際(波羅的海)干散貨運輸市場的BDI和中國集裝箱市場變化趨勢的CCFI等進行了研究.主流的研究方法有：GARCH模型、小波分析理論、支持向量機(SVM)等.GARCH模型能夠衡量波動的非均衡性，但精度無法保證；小波分析理論缺乏適應性，容易受到基函數選擇的約束；SVM等機器學習方法容易出現過擬合導致預測失效[1-2].EMD是一種經驗、直觀、自適應的數據處理方法，能很好地提取非線性和非平穩性數據的時間尺度特征，結合傳統預測方法從而克服單一方法的不足.

文中選取2009年5月—2021年4月YBFI月度數據為樣本，結合“分解-預測-重構”分析思路，將EMD分解后的數據作為樣本，從而降低數據噪聲和網絡復雜性，再對分解序列進行預測，綜合得出最終預測值，從而提高YBFI預測分析的準確性.

1 模型原理

1.1 YBFI序列預測思路

YBFI時間序列具有含噪聲、非線性、非平穩和多尺度性.現今對航運指數研究基本是單一算法預測或針對序列整體進行建模[3]，少有學者對數據的內在波動性出發進行預測研究.預測主要思想為“分解-預測-重構”[4].

采用EMD方法對YBFI序列進行降噪分解，得到不同頻率周期相對穩定的YBFI本征模態分量(intrinsic model function，IMF)和趨勢項(residual)；運用ARIMA模型或者Holt-Winters模型對子序列和趨勢項進行預測，將各個IMF的預測結果進行集成組合即得到最終的YBFI預測結果.YBFI預測模型構建流程見圖1.

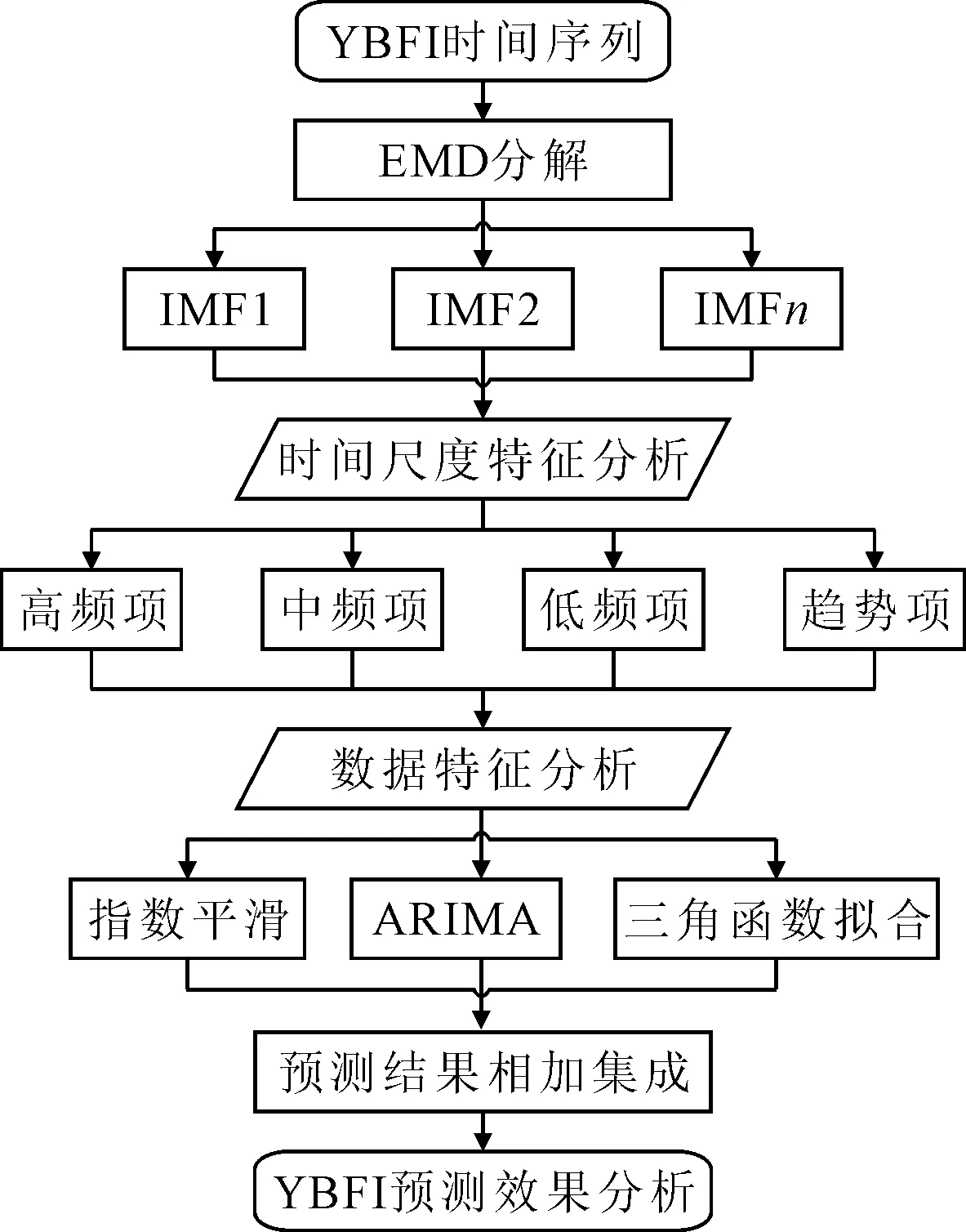
圖1 YBFI預測模型構建流程圖

1.2 經驗模態分解算法

經驗模態分解算法(empirical mode decomposition，EMD)是一種處理非線性、平穩時間序列的前沿時頻分析處理方法[5].分解得到不同波動時間尺度的IMF需同時滿足2個條件：①各分量的極值點確定的包絡線均值為0；②各分量通過極值點的個數與通過零點的個數不多于一個.具體建模步驟見圖2.

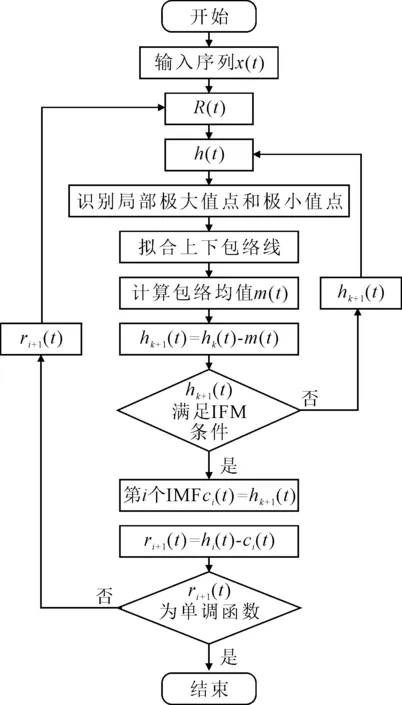
圖2 EMD分解過程

1.3 ARIMA模型

ARIMA模型是將自回歸過程(AR)與移動平均過程(MA)相結合的時間序列組合模型.其識別流程圖見圖3.

圖3 ARIMA模型識別流程圖

該模型的一般表示方式為：ARIMA(p，d，q)×(P，D，Q)S.其中：S為周期步長；d為非季節部分提取趨勢信息所用的差分階數；D為季節部分提取趨勢信息所用的差分階數.乘法模型的實質是通過差分將原始序列化為平穩序列，再對其進行擬合，其模型結構為

式中：{εt}為白噪聲序列；Θ(B)為q階移動平均系數多項式；Φ(B)為p階自回歸系數多項式；▽為差分算子；B為滯后算子.在ARIMA建模過程中，建模的重點在于確定(p，d，q)、(P，D，Q)的值.建模的主要思路[6]為：分析數據特征，對數據進行相應變換，直到通過ADF檢驗獲得平穩時間序列為止，這是ARIMA建模的前提條件；根據ACF/PACF圖形的峰值個數確定模型的參數，根據參數建模預測并對預測結果進行評估.

1.4 預測結果誤差評估標準

根據統計學誤差分析規則，選擇下列7個指標作誤差評價，見表1.

表1 誤差評估指標

2 實證過程

2.1 數據來源及樣本

由于2008年1月—2009年4月數據振幅較大，初步預測結果與現實情況不符.為了準確預測長江航運干散貨2021—2030年的運價指數數據，選取交通運輸部長江航務管理局官網公布的從2009年5月—2021年4月共144個樣本數據.對數據進行初步調整并繪制時序圖，見圖4.

圖4 長江航運干散貨運價指數(YBFI)時序圖

2.2 YBFI序列的非線性、非平穩性檢驗

由圖4可知：數據呈現出較明顯的季節性和波動性，具有明顯的非線性特征.在Eviews軟件中進行ADF非平穩性檢驗，見表2.t統計量(-2.893 456)大于不同顯著水平下的臨界值，在10%置信水平下不拒絕存在單位根的假設，P值(0.167 8)大于0.05，故YBFI序列是非平穩序列.

表2 ADF非平穩性檢驗結果

2.3 EMD分解

EMD方法相比傳統的小波分析、傅里葉分解方法存在一定的優勢，EMD脫離了預定好的基函數的約束，能夠最大程度保留時間序列自身的特性.YBFI序列經EMD分解后得到三個IMF分量和一個趨勢項Residual，見圖5.

圖5 EMD分解結果

由圖5可知：IMF1的波動頻率最高，并依次遞減，平均振幅也從大到小變動，表現出YBFI序列的內在多尺度波動特性.從周期性角度看，IMF1的周期最小，初步分析是市場基礎經濟要素對YBFI序列的影響；IMF2、IMF3依次變大，初步分析IMF2是政府宏觀調控，定期出臺的政策規定對YBFI的影響，而IMF3則可能是航運市場重大事件影響，例如2008年金融危機、2020年新冠疫情等.趨勢項自2008年(根據官網數據可得)便呈現緩慢下降趨勢，到2014年末2015年初達到谷值，之后開始緩慢增長，查閱有關資料，航運市場中周期為10～15年[7]，這與趨勢項展示的規律一致.

2.4 預測和重構

通過EMD分解將YBFI序列分解為相對平穩的IMF分量，將三個IMF分量運用ARIMA模型或Holt-Winters指數平滑法進行比較、預測、分析，此類分析主要在SPSS和Eviews軟件中實現.趨勢項Residual數列采用曲線擬合方法，根據其分布特征和干散貨運輸市場的周期波動特性，運用MATLAB 2018a實驗平臺進行擬合研究，通過訓練，發現三角函數對Residual數列的擬合效果較好.

1) IMF1擬合模型 通過擬合發現ARIMA(2,0,10)×(2,0,0)12能夠很好的反映IMF1序列的波動特性.其擬合優度R2為0.483(接近0.5，擬合較好)，均方根誤差RMSE僅為21.093；DW統計量為2.032；AIC值為9.034.

2) IMF2擬合模型 通過比較ARIMA模型、指數平滑模型以及專家建模結果，發現ARMA(4,7)能對IMF2的周期、波動特性進行很好的預測.其R2達到了一般線性擬合模型R2，為0.996，接近1；均方根誤差RMSE僅為1.257；平均絕對誤差MAE僅為0.803；DW值為1.672；AIC值為3.102.

3) IMF3擬合模型 通過比較擬合發現ARMA(6,1)能對IMF3的特征數列進行較好的擬合.在該模型擬合過程中，R2為0.998，幾乎等于1；均方根誤差RMSE與平均絕對誤差MAE均處于較低區間，DW值為1.912，說明擬合精度較優.

4) Residual擬合模型 趨勢項主要反映了YBFI序列在發展過程中的整體趨勢和變化周期.經過在MATLAB實驗平臺中反復驗算，調參，最終確定該序列的較優擬合、預測模型方程式為

Residual-PREt=778.2+14.49×

cos(t×0.027 86)-95.89×sin(t×0.027 86)+

24.64×cos(2×t×0.027 86)+

22.71×sin(2×t×0.027 86)-3.695×

cos(3×t×0.027 86)+0.497 1×

sin(3×t×0.027 86)

式中：Residual_PREt為第t期趨勢項Residual的預測值；t為時間序號，記2009年5月為t=1；依次往后t=2，3，…，n.

圖6為Residual的擬合預測模型效果和殘差分析圖.

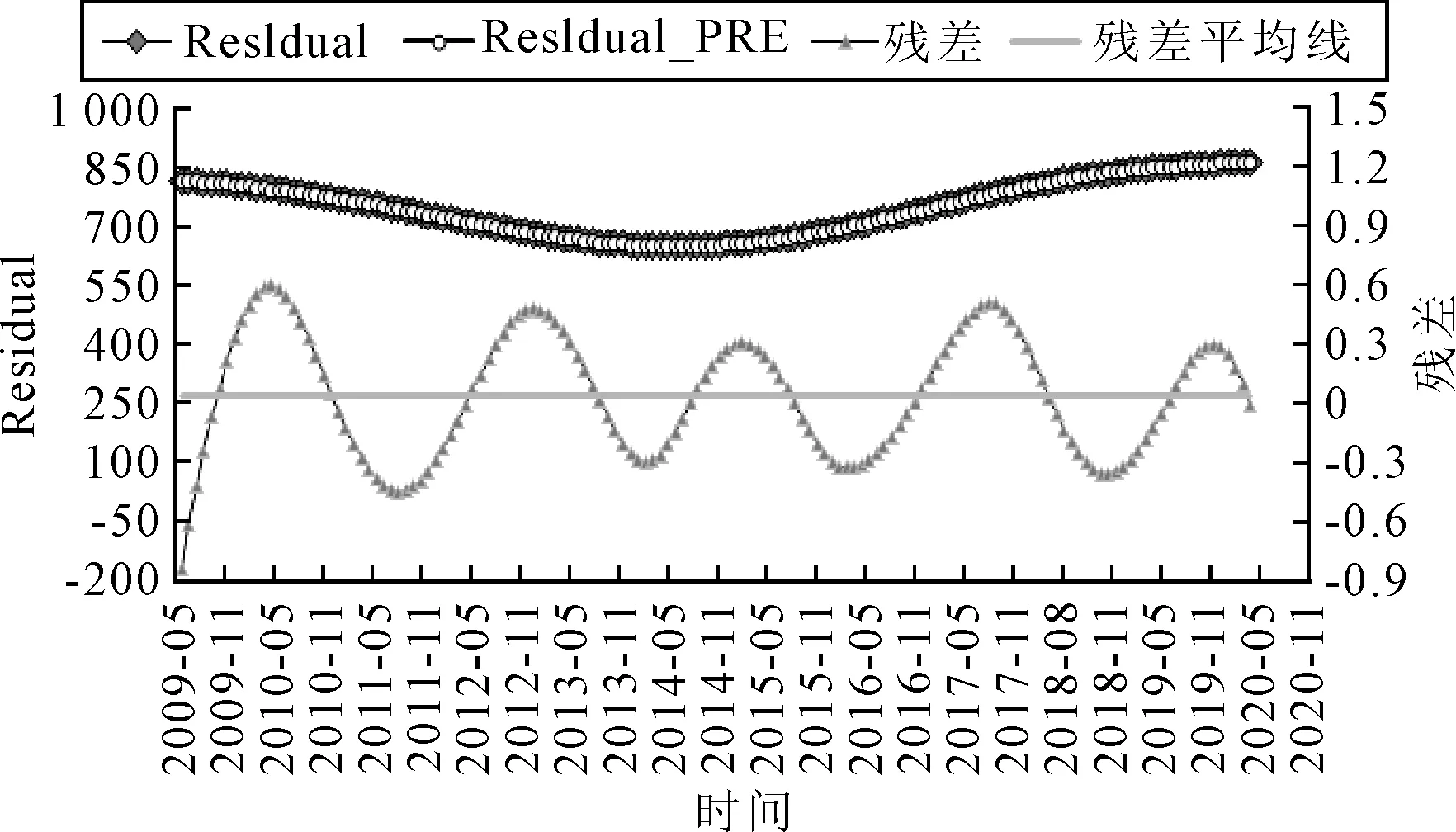
圖6 Residual擬合與殘差分布

從殘差分布曲線，發現擬合效果較好，殘差基本在[-0.95，0.60]之間，且平均殘差僅為0.036 09，與0無明顯差異.

5) YBFI預測結果 由式(1)，將上述經驗模態分量和趨勢項求和即可得到相應年份YBFI預測結果，見圖7.

圖7 YBFI擬合效果圖

預測值略有滯后，但基本能夠反映樣本波動規律和變化趨勢.通過計算，得到殘差均值僅為0.312 8(與0無明顯差異)，說明總體誤差水平較低；均方根誤差RMSE為20.317，若以基期1 000點算，均方根誤差僅為2%，說明高值部分預測效果較好；平均相對誤差絕對值MAPE為1.62%，在10%范圍內，表明平穩部分預測效果較好；平均絕對誤差MAE=12.184；相對誤差RE中僅有五組數據超過5%，2組數據超過10%，占樣本總數的比例分別為0.034 7、0.013 9，可忽略不計，故可判斷整體誤差較低；R2為0.973 5，說明該模型對YBFI序列的預測效果較準確.

2.5 結果分析

將EMD-ARIMA組合模型相關參數與傳統、單一的季節性預測方法[8]進行對比，見表3.

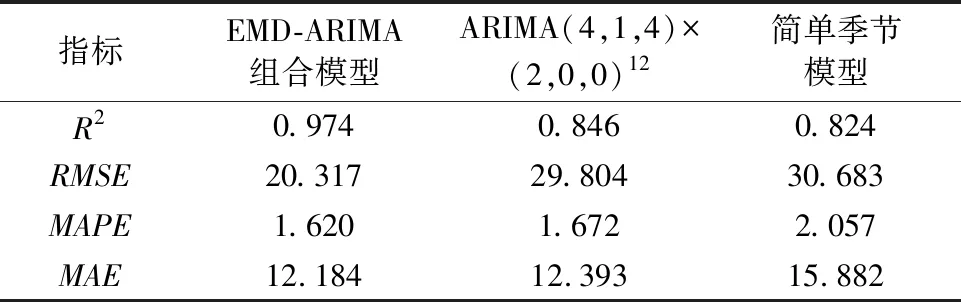
表3 EMD-ARIMA組合模型及其對比模型預測誤差比較

總體來看，相比ARIMA模型和簡單季節模型，EMD-ARIMA組合模型對YBFI序列的預測表現更優，說明EMD分解能有效提取含噪聲、非線性、非平穩性數據的時間尺度特征，通過對本征模態變量IMF和趨勢項Residual的預測結果進行重新組合，可以得到準確的YBFI預測結果.

該模型對未來年份YBFI預測結果(部分)見表4.

表4 未來年份預測結果

由表4可知：2022—2023年，YBFI將達到一個較高水平，之后又緩慢下跌，在不考慮“通貨膨脹”等因素的情況下，預計2030年的YBFI將處于一個較低的水平.根據我國內河運輸的長期發展現狀來看，在未來很長一段時間內，若沒有較大的技術突破，干散貨航運市場將維持原來的周期波動規律，整體略有上漲趨勢.

3 結 論

1) EMD模型能有效分解YBFI序列，在保留數據自身的內在波動特性的同時對不同波動頻率數據進行分解，為后續預測操作提供周期較穩定的分解序列.

2) EMD-ARIMA組合模型的相對誤差RE中超過5%的樣本僅占樣本總數的0.0347，其整體誤差水平基本在5%內.

3) EMD-ARIMA組合模型預測效果和精度均優于傳統單一的時間序列預測方法.在預測精度和擬合優度方面提高了將近15%，平穩部分和中高值預測效果均得到較大幅度提升，其RMSE、MAPE、MAE值(相比單一ARIMA模型)分別下降了31.83%、3.11%、1.69%.

本方法可利用有限數量樣本，較好模擬出長江干散貨運價指數周期性不明顯、非線性、非平穩的波動特性，為長江干線散貨運輸市場發展態勢預測提供支持.