不受姿態誤差影響的慣性/磁感應融合定位方法

李新年，李清華，王常虹，鄭元勛，王振桓，夏子權

（1.哈爾濱工業大學 空間控制與慣性技術研究中心，哈爾濱 150001；2.中國兵器工業集團航空彈藥研究院，哈爾濱 150030）

科技的高速發展在便捷人類生活、拓展人類生存空間的同時，對現有技術提出了更高的功能與指標。導航定位技術作為一種基礎技術，在物聯、機器人等新興研究領域中起著重要的作用[1,2]，然而由于室內等復雜場景存在非視距、多徑等影響因素，現有GPS、UWB等技術難以實現無累積誤差的高精度定位服務。根據電磁信號的波粒二象性可知，磁場穿透能力與頻率成反比，因此基于高穿透低頻磁場的定位方法是實現室內場景高精度定位的有效方案之一[3-5]。低頻磁場定位信號一般由通電螺線管、旋轉永磁體等人工磁信標產生，經分析，其在空間的磁場分布與相對位置存在確定性數值關系，基于此，本文提出了一種磁感應室內定位方法。

基于人工磁信標的磁感應定位方法主要圍繞磁感應強度、磁感應矢量[6-17]兩個角度開展研究。磁感應強度所提供的定位信息少于磁感應矢量，因此基于磁感應矢量的人工磁信標定位系統的復雜度通常要低于基于磁感應強度的定位系統。然而基于磁場矢量的磁信標定位系統受傳感器姿態影響，通常需要結合其它輔助信息來獲取姿態信息，進一步解算目標位置。基于慣性傳感器[6-11]、多磁信標/傳感器的幾何信息[12-17]常被用來輔助磁信標定位系統，如Pasku等人[9]利用磁強計與慣性傳感器設計了一種組合導航系統，慣性傳感器通過敏感姿態數據輔助磁傳感器轉換磁感應矢量，并結合磁場分布模型與空間幾何構型建立磁信標定位模型，實現對目標位置的估計；鄭元勛等人[12-14]采用多個位置姿態已知的人工磁信標構建出具有明確幾何信息的磁感應定位系統，達到對目標位置姿態的估計。然而輔助信息源的設計不僅增加了系統的復雜度，而且直接從其它信息源獲取的姿態信息被用來轉換磁感應矢量時，其姿態誤差會對磁感應定位精度造成影響。

為解決磁信標定位系統受傳感器姿態誤差影響的問題，本文建立了一種與傳感器姿態無關的磁信標定位模型；并基于此，結合慣導模型提出了一種改進的慣性/磁感應的定位方法，通過無跡卡爾曼濾波[18-20]（Unscented Kalman Filter,UKF）算法和磁信標磁場數據實現了對慣導一步預測結果的修正，提高了定位精度、定位結果的輸出速度和穩定性。

1 磁感應定位模型

1.1 雙軸磁信標定位模型

人工磁信標系統主要由磁源、傳感器與導航解算單元三部分構成，而由磁源產生的低頻磁場又是定位信息的傳播媒介，其分布規律是分析定位方法的理論基礎。本節將結合畢奧-薩伐爾定律與磁偶極子模型對雙軸磁信標的磁場分布進行理論分析。依據磁偶極子模型將通電螺線管視為圓形載流回路，當環境中的磁導率為0μ，通電螺線管的激勵電流幅值為I，信號頻率為ω，線圈匝數為N，則根據畢奧-薩伐爾定律，磁偶極子磁矩指向與信標坐標系中z軸的指向相同時，空間中任意一點處P（x,y,z）單軸螺線管的磁感應矢量的表達式為：

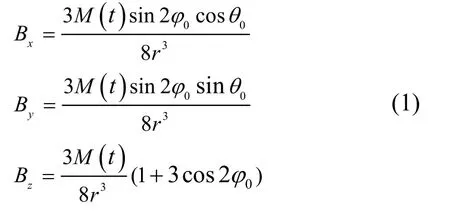
其中r為目標點P到坐標原點O的相對距離，為俯仰角，為相對方位角[5]，為通電螺線管磁矩，人工磁信標與目標點之間的相對位置如圖1所示。

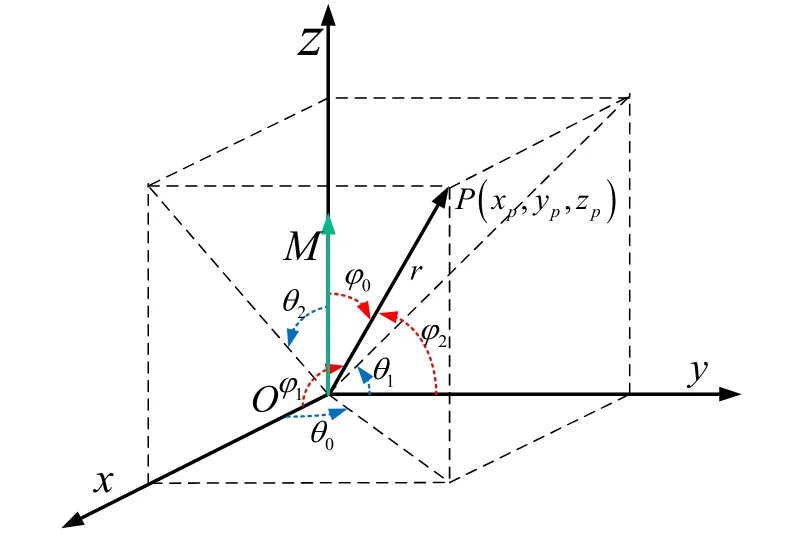
圖1 信標中心與目標點之間的相對方位Fig.1 Relative position from center of beacon to the target

圖中1φ、2φ、0φ分別為磁信標與目標點之間相對于x軸、y軸、z軸的俯仰角，1θ、2θ、0θ分別為磁信標與目標點之間相對于x軸、y軸、z軸的偏航角，根據長方體中的邊角關系，可以獲得如下轉換關系：

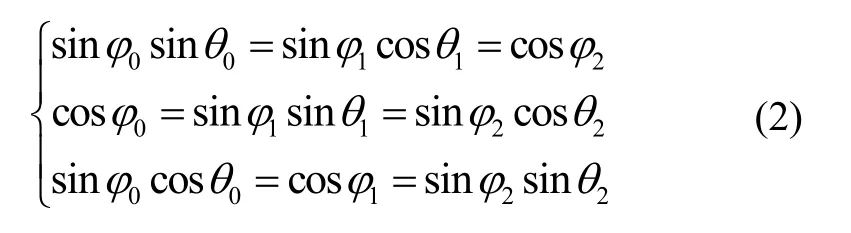
根據螺線管軸數，常見的磁信標可以分為單軸磁信標、雙軸磁信標和三軸磁信標；基于磁場矢量的單軸磁信標不足以實現定位，而三軸磁信標存在成本高、空間結構復雜等缺點，因此本系統采用雙軸正交螺線管磁信標作為磁源，其空間結構如圖2所示。

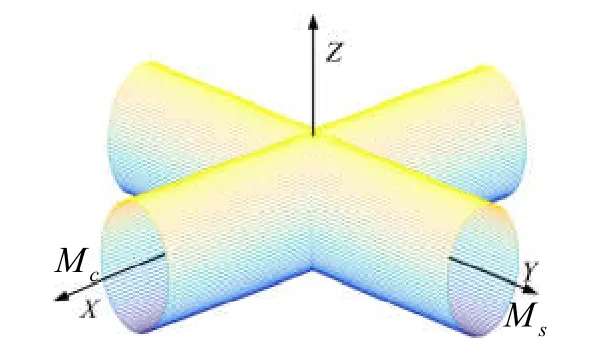
圖2 雙軸磁信標結構形式Fig.2 The structure of dual-axis magnetic beacon

基于單軸螺線管的磁感應矢量表達式(1)、相對方位角之間的轉換式(2)以及雙軸磁信標結構形式，雙軸磁信標中兩個通電螺線管在空間中點產生的磁場可以分別表示為：

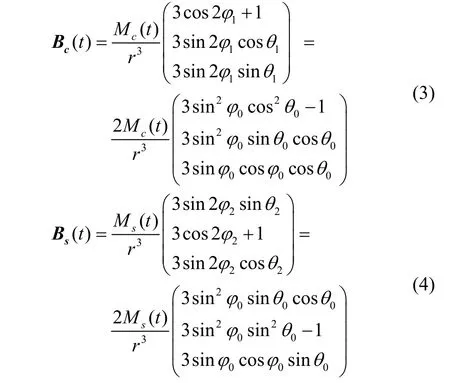
依據雙軸磁信標在空間中任意一點的磁場矢量表達式和高維空間中橢圓的基本方程可以分析出，空間中任意一點的磁場矢量隨時間呈橢圓平面變化，該橢圓平面具有唯一方向不變的特征矢量，該特征矢量可以通過式(5)進行提取。

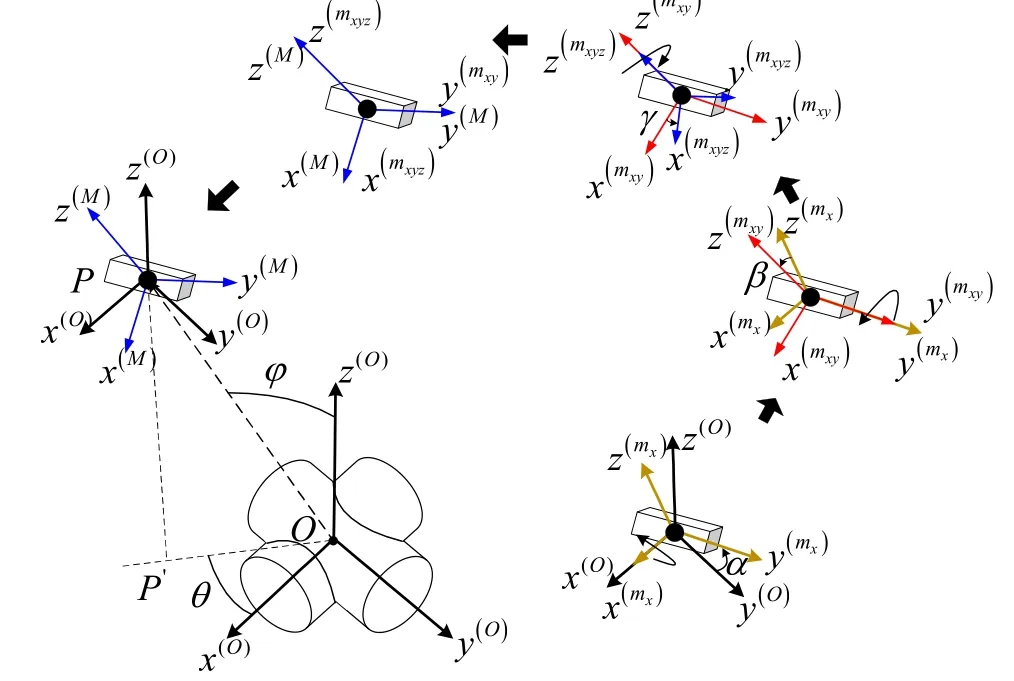
圖3 傳感器坐標轉換過程Fig.3 Process of magnetic sensor attitude translation

為避免傳感器載體坐標系與信標坐標系不一致對定位精度的影響，根據幾何理論中矢量內積相關知識，可以得到如下不受影響的磁場矢量與位置相關表達式：

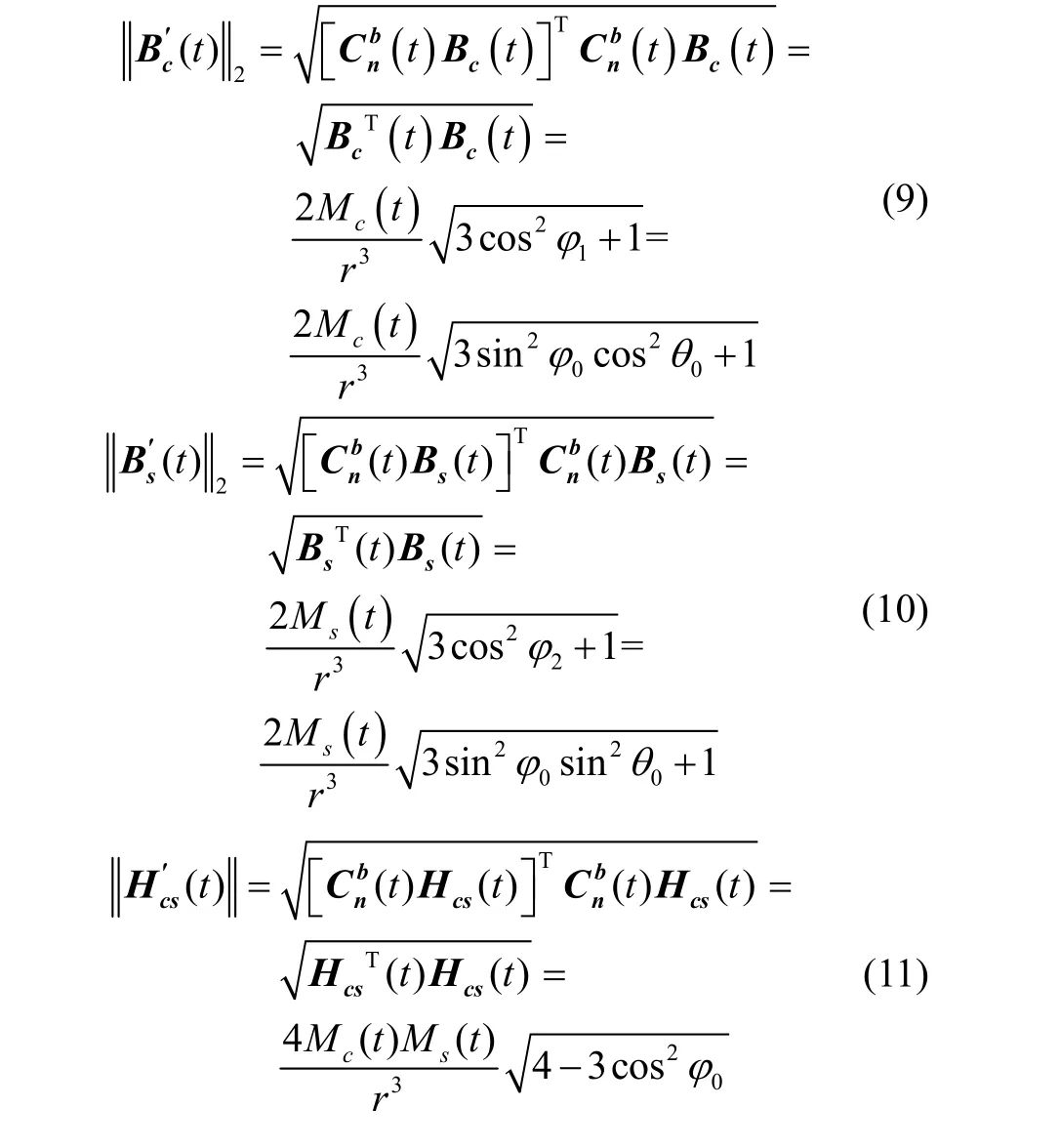
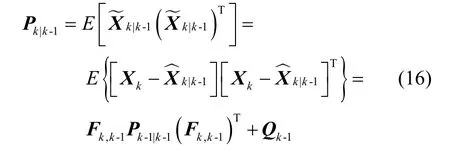
根據磁場傳播特性，式(9)-(11)可以簡化為雙對數表達式：

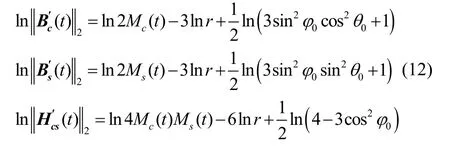
基于式(12)，可以構建如下定位模型：

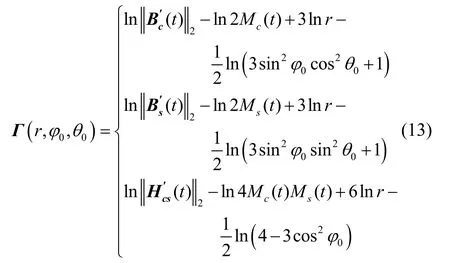
1.2 基于UKF的慣性/磁感應定位

基于磁場分布規律，本文在1.1節分析了一種不受傳感器姿態影響的雙軸磁信標定位模型，能夠以較高的精度實現對靜態目標位置的估計，然而磁信標定位方法往往需要整周期的磁場數據解算目標位置，輸出速度不能滿足動態目標需求，因此本文基于無跡卡爾曼濾波算法提出了一種融合慣性數據和磁感應矢量的定位方法，慣性/磁感應定位模型可以表示為：

改進的慣性/磁感應定位模型是一種不存在累計誤差的定位模型，慣性元件的一步預測誤差是由器件自身的零偏、隨機游走、標定誤差等因素造成的，是一種隨時間逐漸增加的累計誤差。短時間內，慣性元件的一步預測結果接近真實位置，能夠為磁感應定位方法求解目標位置提供參考值，而低頻磁場定位模型能夠實現對慣性元件的一步預測結果的修正，二者的融合使慣性/磁感應定位方法的誤差在一定范圍上下波動。

根據式(14)可以分析出，利用慣性/磁感應技術對動態目標進行定位的過程可以被建模成典型的非線性動態模型。EKF、UKF及智能優化（群智能）算法是解決非線性動態系統問題的主流方法，EKF是一種利用函數近似的思路進行非線性濾波的方法，由于EKF對非線性強度高的系統濾波存在較大模型誤差；智能優化算法是利用多個智能體的自身狀態與目標狀態之間的差距不斷調整、優化自身以實現對目標狀態進行最優估計的一種搜索方法，存在尋優速度較慢，每一次尋優需要遍歷所有智能體后才能完成，計算資源需求高等問題。UKF是一種對后驗概率密度進行近似的次優濾波算法，降低了系統模型誤差，且能夠以較少的計算資源和較高的計算效率逼近非線性系統的結果。因此，采用UKF算法對慣性/磁感應模型進行濾波估計，在保證定位精度的同時，提升計算效率。

根據慣性/磁感應定位模型(14)，系統狀態噪聲kV與量測噪聲kW無關，且為零均值高斯白噪聲，則一步預測誤差協方差為：

進行Sigma采樣，并對磁感應矢量進行一步預測：

磁感應矢量的一步預測均值、量測預測誤差協方差以及狀態預測誤差和量測預測誤差的互協方差為：

基于UKF的慣性/磁感應定位方法流程圖如圖4所示。

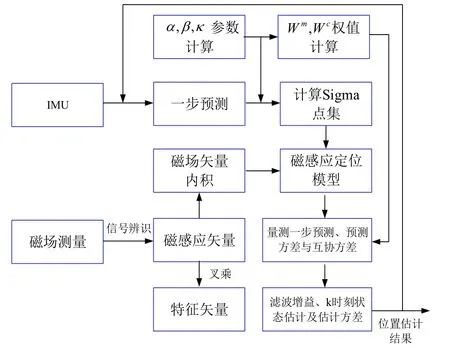
圖4 慣性/磁感應定位流程圖Fig.4 Inertial magneto-i nductivepositioning flow chart

2 實驗驗證

不受傳感器姿態影響的磁感應定位模型與基于UKF的慣性/磁感應融合定位方法為本文的兩個主要研究目標，本節將通過實驗的方式對磁感應定位模型有效性和精度進行驗證，由于實際測試過程中目標的真實動態軌跡很難給出，因此本節將采用數值仿真的方式對慣性/磁感應定位方法進行仿真驗證，將文獻[9]中IMU解算的姿態輔助磁信標定位方法與本文提出的改進慣性/磁感應定位方法對動態目標的運動軌跡估計結果與真實軌跡進行對比，從而達到驗證基于UKF的慣性/磁感應定位方法精度的目的。

2.1 磁感應定位模型實驗驗證

本節將利用如圖5所示的雙軸磁信標實驗系統測試磁感應定位模型，整個系統由信號生成單元、線性功率放大器、雙軸磁信標、磁傳感器探頭與數據處理模塊、定位解算計算機5部分構成，激勵電流幅值均為4 A、頻率均為20Hz，相位相差90°，磁傳感器感知范圍為0.1 nT-10000 nT，磁信標軸線長度為35cm，螺線管直徑為15cm。系統導航坐標系以磁信標幾何中心為原點，磁信標坐標系與全局坐標系重合，磁傳感器在全局坐標系第一象限內，坐標系指向與圖5中坐標軸一致。實驗過程中磁信標底面與傳感器之間的高度相差0.82m，傳感器位置每次向x軸或y軸移動0.6m，在同一位置處傳感器采集3次磁場矢量，磁傳感器所在的坐標系與磁信標所在坐標系的偏航角分別成0°、60°和120°角度，輸入定位解算計算機中進行解算，以測試不受傳感器姿態影響的磁感應定位模型有效性與定位效果。

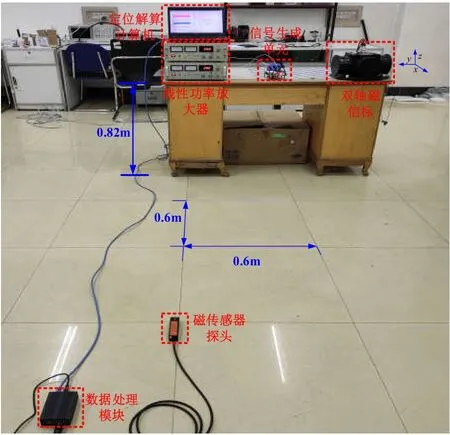
圖5 實驗系統Fig.5 Experimental system

根據式(13)的非線性磁感應定位模型對磁傳感器位置進行估計，利用Levenberg-Marquardt方法通過迭代的方式估計非線性方程組最優解，實驗結果如圖6所示，第1組磁場矢量解算結果為傳感器坐標系與信標坐標系一致時（即偏航角夾角為0°）的位置估計，第2、3組為傳感器坐標系與磁信標坐標系夾角分別為60°和120°時的估計結果。根據以上實驗的結果可以看出，利用磁感應定位模型能夠準確地估計出傳感器與磁信標之間的相對位置，且位置估計結果不受傳感器姿態的影響。

圖6 靜態目標定位結果Fig.6 Positioning resultsof static tar get

2.2 慣性/磁感應定位方法數值仿真驗證

在前一節實驗中驗證了本文提出的磁感應定位模型的可行性，本節將通過數值仿真的方式驗證基于UKF的慣性/磁感應定位方法。設IMU和磁傳感器是坐標系一致的剛性連接，兩者之間質心重合，磁場數據包括磁信標磁場、地磁場和環境中干擾磁場，磁信標磁場數據由磁偶極子模型和估計的雙軸螺線管磁矩參數產生，短時間內磁場數據可以視為常值，根據實驗室測量地磁場強度約為40000 nT，干擾磁場可視為白噪聲約為0.5 nT，磁傳感器信號采樣率為1000 Hz，慣性元件指標為：（1）加速度計的零偏不穩定性為9.8 ×10-2m/s2；（2）陀螺儀的零偏不穩定性為8 °/h；（3）慣導數據輸出速率為1000 Hz。依據上述數據模型和相關參數，以給出的實際路徑為基礎生成磁場數據和慣性導航系統數據。該仿真將文獻[9]中的傳統慣性/磁感應定位方法，即通過IMU解算的姿態信息對磁場矢量進行轉換再進行融合定位的方法，與本文提出的不受傳感器姿態影響的改進慣性/磁感應定位方法進行對比分析，以達到驗證磁感應定位模型有效性和測試慣性/磁感應定位方法性能的目的。

仿真結果表明，結果輸出速度方面：由于僅依靠磁感應定位方法需要整周期的磁場數據進行位置解算，位置結果的輸出頻率低于20 Hz；本文提出的慣性/磁感應定位方法結果解算時間低于8 ms，即輸出頻率高于125 Hz，慣性/磁感應融合定位方法提高了磁感應定位方法的位置估計結果輸出速度。定位精度方面：數值仿真誤差如圖7所示，兩種定位方法誤差的累積概率分布如圖8所示。

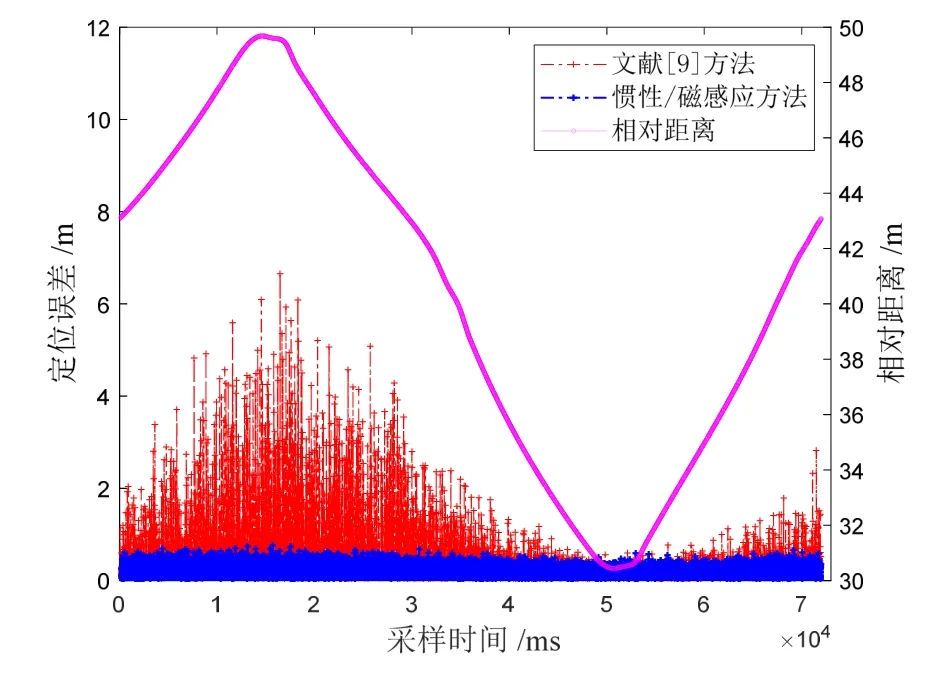
圖7 動態目標定位誤差Fig.7 Positioning errors of moving target

動態目標定位誤差和誤差累積概率分布的結果表明，慣性/磁感應融合定位方法能夠避免累計誤差，且本文提出的改進慣性/磁感應定位方法與文獻[9]采用的傳統慣性/磁感應定位方法相比，傳統的慣性/磁感應融合方法定位誤差隨著相對距離的增加而增大，由式(13)分析可得出：隨著距離的增長，磁場信號信噪比降低，姿態解算誤差對磁信標定位方法的影響增大。在磁信標有效作用域內，本文提出的方法定位性能優于傳統慣性/磁感應方法，不會受傳感器姿態解算誤差的影響，定位結果在一定范圍內成上下波動的變化。誤差累積概率分布如圖8所示。

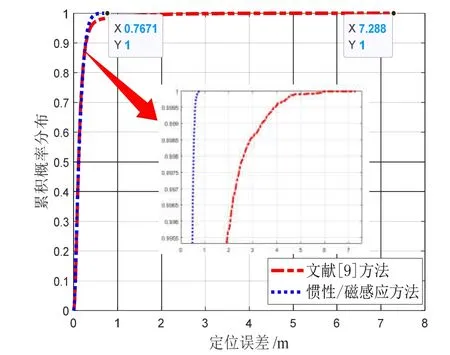
圖8 動態目標定位誤差累積概率分布Fig.8 The cumulative probability distribution of moving target positioning errors

文獻[9]和本文提出方法的定位誤差低于0.5 m的

概率為95%，文獻[9]方法最大估計誤差為7.3 m，本文提出的基于UKF慣性/磁感應融合方法的最大估計誤差為0.77 m。由此看出在磁場信號信噪比低于一定程度時，傳感器姿態誤差對磁信標定位方法造成的影響增大，而本文提出的慣性/磁感應定位方法一方面避免了傳感器姿態對系統定位的影響，另一方面實現了慣導數據與磁感應數據的融合，提升了系統定位性能。

3 結論

針對基于磁感應矢量的電磁信標定位系統定位精度受限于傳感器姿態的問題，本文提出了一種改進的慣性/磁感應定位方法，有效避免了傳感器姿態誤差對磁信標定位系統造成的影響，并通過實驗與仿真結合的方式驗證了方法的有效性。主要內容如下：

（1）基于磁信標的磁場分布規律和特征矢量建立了不受傳感器姿態影響的磁感應模型，給出了該模型的詳細分析過程，并通過實驗驗證了模型的有效性。

（2）提出了一種基于UKF的改進慣性/磁感應融合定位方法，實現了慣導數據與磁感應數據的融合，提升了系統估計目標位置的速率和定位性能，并通過仿真驗證了方法的性能。

本文提出的改進慣性/磁感應定位方法實現了慣性導航與磁感應定位的優勢互補，為室內等復雜場景的高精度定位系統的開發提供了思路。