基于PCA-VMD-CNN的輸電線路覆冰重量預測模型*

李 波，李 鵬，高 蓮，楊家全，包慧琪

(1.云南大學 信息學院，云南 昆明 650500；2.云南省高校物聯網技術及應用重點實驗室，云南 昆明 650500；3.云南省電網有限責任公司，云南 昆明 650217；4.云南大學 軟件學院，云南 昆明 650500)

0 引言

覆冰作為1種自然現象，給世界各地輸電線路造成嚴重破壞，其可以引起導線舞動、金具破壞、跳閘停電、電桿倒、導線折斷等事故。因覆冰負荷超限造成高壓輸電線路倒(桿)、線路拉斷等事故時有發生[1-3]。

目前國內外已開展大量研究工作并取得了較大進展。文獻[3]從空氣動力學和熱力學角度出發提出最優時間步長模型，然而需要大量微觀參數才能保證預測精度；文獻[4-5]基于傳統時間序列分析的方法構建預測模型，模型對處理平穩的覆冰過程效果尚可，但對非平穩狀態下的覆冰過程預測效果欠佳，抗干擾能力差；文獻[6-10]基于影響覆冰負荷的氣象因素建立機器學習回歸模型，然而氣象數據的采集誤差較大[11]，只用氣象數據建立的回歸模型預測精度有限。

因此，本文建立1種基于PCA-VMD-CNN的輸電線路覆冰短期的預測模型。首先對氣象因素進行主成分分析(Principal Component Analysis,PCA)，降低數據維度，然后對覆冰歷史重量進行變分模態分解(Variational Modal Decomposition,VMD)，將原始覆冰重量分解為不同變化趨勢的分量[12-13]，并根據每個分量建立卷積神經網絡(Convolutional Neural Network， CNN)模型分別進行預測，再將各分量分別預測的結果疊加組合得到預測的最終值。本文模型既考慮影響導線覆冰重量的氣象因素，又考慮歷史覆冰的影響以及覆冰過程的非平穩態，以期為電力系統的安全可靠運行提供更可靠的覆冰預警。

1 基本原理

1.1 主成分分析

主成分分析是處理高維數據的1種統計學習方法，對數據矩陣的協方差矩陣進行特征值分解，達到降維的目的。PCA主要分為4個步驟。

原始數據矩陣如式(1)所示：

(1)

式中：n為數據個數；p為特征數。

1)數據標準化(中心化)的矩陣X*表示如式(2)：

(2)

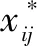
2)計算標準化后的協方差矩陣R，如式(3)所示：

(3)

3)求R的特征值和特征向量。

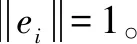
4)計算主成分貢獻率及累計貢獻率。貢獻率計算如式(4)，累計貢獻率計算如式(5)所示：

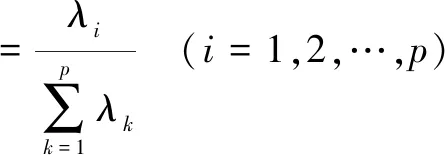
(4)

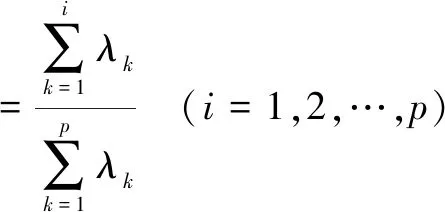
(5)

選取累積方差貢獻率在75%～95% 時，對應的前q個主成分包含原始p個變量所能提供的絕大部分信息。

1.2 變分模態分解

變分模態分解算法(VMD)由Dragomiretskiy提出，是1種自適應而且通過迭代搜索的信號分解技術。VMD可以將原始信號f(t)分解為具有不同中心頻率和帶寬的子信號，每1個子信號都是原始數據的1個本征模態函數(IMF)。每1個IMF表示原始信號在不同尺度下的變化趨勢。對于信號f(t)的約束變分模型如式(6)所示：

(6)

式中：uk為第k個IMF分量；wk為第k個IMF分量的中心頻率；dt為函數時間導數；δ(t)為單位沖激函數；j為虛數單位；t為時間變量；?為卷積運算。

引入懲罰因子α和拉格朗日懲罰算子λ，約束變分問題就轉為非約束性變分問題，如式(7)所示：

(7)

VMD求解過程如下：

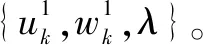
2)采用乘子交替算法更新{uk},{wk},λ。

3)給定精度ε，若滿足精度則停止更新，如式(8)所示；否則繼續更新。

(8)

1.3 卷積神經網絡

卷積神經網絡(CNN)是1種前饋網絡，由卷積層、池化層、全連接層和輸出層組成，圖1為CNN結構模型。

圖1 卷積神經網絡模型Fig.1 Model of convolutional neural network

卷積層是CNN的核心，在卷積層上，卷積核通過設定的移動步長完成對各輸入特征圖的卷積濾波，提取局部特征，輸出特征圖。運算公式如式(9)所示：

Y=Relu(W?X+B)

(9)

式中：X為輸入特征；W為卷積核；?為卷積運算；B為偏置；Relu為激活函數:Relu(x)=max(0,x)。

卷積運算過后對特征圖進行池化操作，在一定范圍取最大值或平均值，池化可以減少模型參數，防止過擬合。

在全連接層上,把從輸入點展開的一維特征矢量經過加權求和，使用激活函數計算得到，如式(10)所示：

yk=Rule(ωkxk-1+bk)

(10)

式中：yk為輸出；k為第k層全連接層；ωk為連接權重；xk-1為展開的一維圖；bk為偏置。

CNN采用梯度下降法來更新ω，b使損失函數達到最小，損失函數選擇均方差損失函數如式(11)所示：

(11)

式中：N為樣本數量；y為樣本標簽；Relu(ωx+b)為通過全連接層的輸出值。

2 輸電線路覆冰重量預測模型

本文預測模型的基本思想是通過覆冰歷史重量及當下氣象數據來預測覆冰數據，可分為以下5個部分：

1)數據預處理。

2)氣象數據主成分分析。

3)將歷史數據通過VMD分解為多個IMF分量。

4)將氣象數據和歷史覆冰重量各個IMF組合為新的輸入矩陣。

5)將輸入矩陣輸入到CNN模型，將每個分量的預測結果相加。

具體流程如圖2所示。

圖2 VMD-CNN覆冰預測流程Fig.2 Flow chart of ice coating prediction by VMD-CNN

2.1 數據預處理

為降低異常數據對預測的干擾以及避免不同特征之間數值差距太大，提高收斂速度，本文對數據進行以下處理。首先，輸電線路結冰的基本條件是溫度<0 ℃，相對濕度>80%等，根據此依據剔除異常數據[8]；其次，進行數據歸一化。

本文將數據歸一化到(0,1)之間，如式(12)所示:

(12)

式中：yg為歸一化后得到的數據；y為歸一化的原始數據；ymax為原始數據的最大值；ymin為原始數據的最小值。

2.2 構造輸入矩陣

設提取的主成分為W=[w1,w2,…,wq]，q為提取的主成分個數。設輸入的N個歷史覆冰重量T=[t1,t2,…,tn]。將前n個歷史數據和第n+1時刻的氣象數據構造為輸入矩陣預測第n+1時刻的覆冰重量。輸入矩陣如式(13)所示：

(13)

由于卷積神經網絡的優點在輸入圖像時表現的更為明顯，因此將輸入構造為二維矩陣輸入到卷積神經網絡里進行訓練和預測，經實驗證明，構造為二維矩陣可以提高預測精度。

2.3 多步長預測

多步長預測是建立在15 min的單步預測基礎上，假設天氣因素不變，將前一步長預測中得到的覆冰重量預測值作為實際值代入，圖3為多步長預測流程。

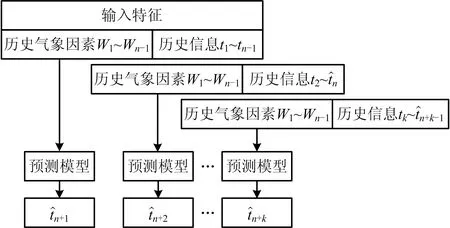
圖3 多步長預測流程Fig.3 Flow chart of multiple step size prediction

2.4 評價指標

本文采用均方根誤差RMSE、平均絕對誤差MAE和決定系數R2對模型進行評價。RMSE和MAE越小越好，R2表示模型的擬合效果，越接近于1，擬合效果越好[14]。

均方根誤差(RMSE)計算如式(14)所示：

(14)

平均絕對誤差(MAE)計算如式(15)所示：

(15)

決定系數(R2)計算如式(16)所示：

(16)

3 實例分析

3.1 數據來源

為驗證模型的有效性和可行性，本文選取某電網公司輸電線路在線監測系統采集的覆冰過程中數據進行模型驗證，如圖4所示。本文數據采樣間隔時間均為15 min， 圖4～6、圖8～9橫坐標數字表示采樣次數，即第x個15 min。

3.2 光照強度處理

由于光照強度的特殊性(夜晚會驟降到0)，直接代入模型會影響光照和覆冰之間的相關性，因此對光照強度應取1天的平均值來代替原始值。圖5為光照強度處理前后對比結果。

圖4 覆冰過程Fig.4 Process of ice coating

3.3 主成分提取

將6個氣象因素進行主成分分析。得到6個變量的協方差矩陣以及主成分累計貢獻率如表1所示。

圖5 光照強度處理結果Fig.5 Processing results of light intensity

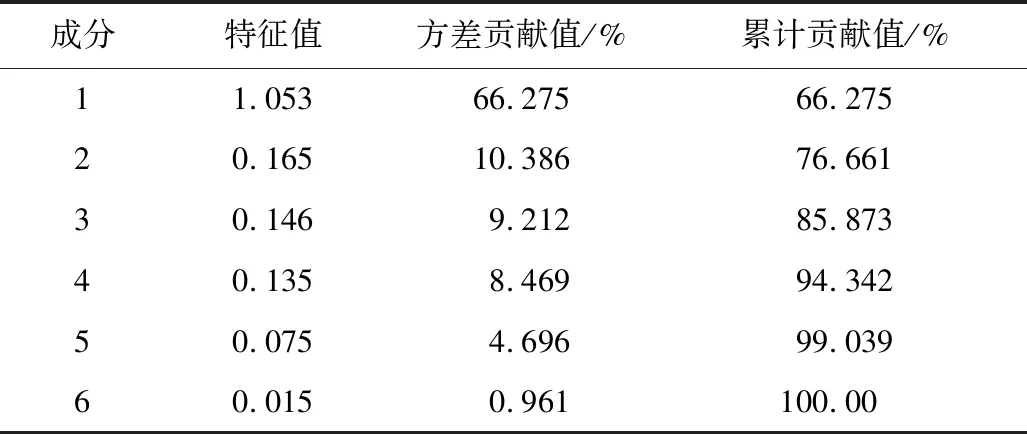
表1 6個變量協方差特征值Table 1 Covariance eigenvalues of six variables

由表1可知，前4個主成分的貢獻率達到94%，可以解釋原始數據絕大部分信息，因此提取前4個主成分作為模型輸入。

3.4 VMD分解

將歷史覆冰數重量分解為6個IMF分量，圖6為原始數據與分解結果。

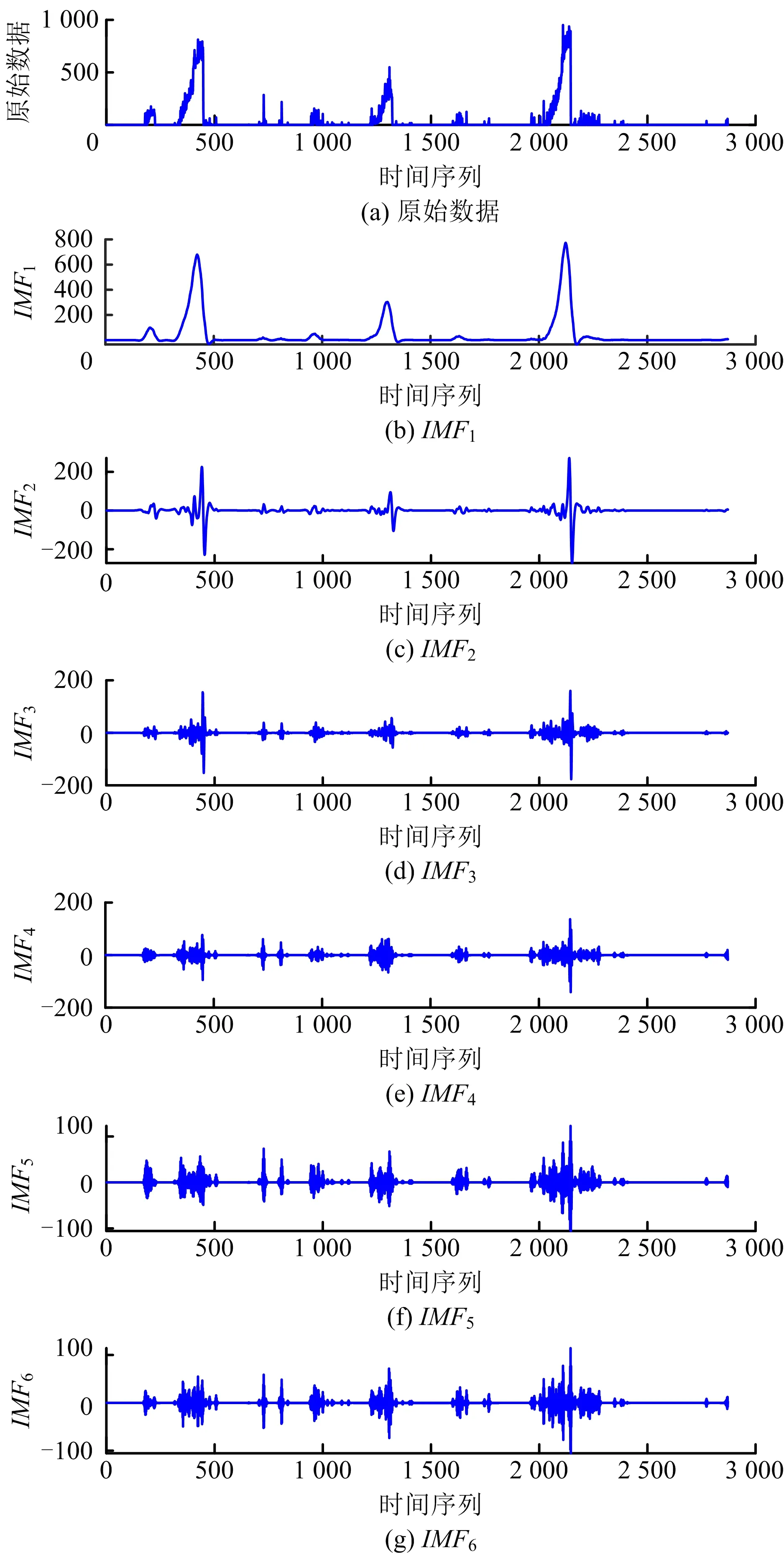
圖6 原始數據與VMD分解結果Fig.6 Original data and results of VMD decomposition

3.5 卷積神經網絡參數的設置

如上文所述，本文利用前n個歷史覆冰重量和第n+1時刻的氣象數據作為模型輸入，第n+1時刻的覆冰重量作為期望值與模型預測值進行誤差比較。為尋找最佳n的值，采用均方根誤差作為評價指標，即RMSE越小，訓練效果越好。圖7為不同n值下的訓練集的RMSE的大小。由圖7可以看出，當n為6時，訓練集均方根誤差最小。

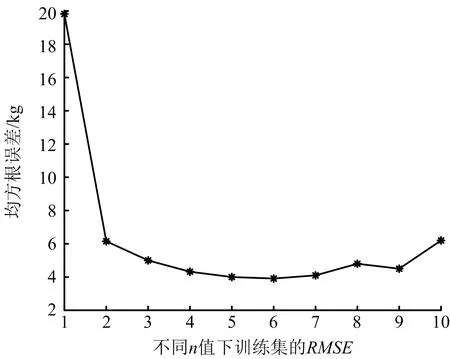
圖7 不同n值下訓練集的RMSEFig.7 RMSE of training sets under different n values

卷積神經網絡的輸入為十維(前6個時刻的覆冰重量加上4個主成分)，通過式(13)構造為10×10輸入矩陣。因此，輸入層大小為10×10，卷積核大小選為3×3×16(16為卷積核層數)，池化層大小為2×2，通過簡單計算，輸入通過卷積層化之后的大小為4×4×16，展開為256×1的向量輸入到全連接層，全連接層的隱藏層神經元第1層選取16個，第2層選取4個，輸出層神經元個數為1。

3.6 預測結果對比

為分析本文模型的優勢，選取LSTM(長短期記憶人工神經網絡)，LSSVM(最小二乘支持向量機)[8，15]，WNN(小波神經網絡)[6]，CNN與本文模型進行對比。由圖4可知，數據的第2 022到2 162之間覆冰最嚴重，所以本文選取1到2021個數據為訓練集，2 022到2 162個數據為測試集進行單步和多步預測。

單步長預測結果如圖8所示。表2為6種模型單步長評價指標對比。表3～5分別為6種模型的多步長預測評價指標對比結果，圖9為模型單步長絕對值誤差對比結果。

由圖8可知，當預測步長為1時，6種模型的預測曲線與實際值基本一致，基本可以反映實際覆冰重量。由表2可以看出，本文模型明顯降低了誤差，提高預測精度，對比圖9的誤差曲線不難看出，WNN,LSSVM,LSTM模型的前85個測試樣本絕對值誤差在100 kg上下浮動，CNN在50 kg左右浮動，而本文模型僅在20 kg上下浮動。測試集數據中，WNN,LSSVM,LSTM,CNN 4種模型最大絕對值誤差均超過200 kg，本文模型(二維)絕對值誤差僅為46 kg；并且，在對覆冰最大值進行預測時，其他4種模型絕對值誤差均超過30 kg，本文模型僅為6 kg。

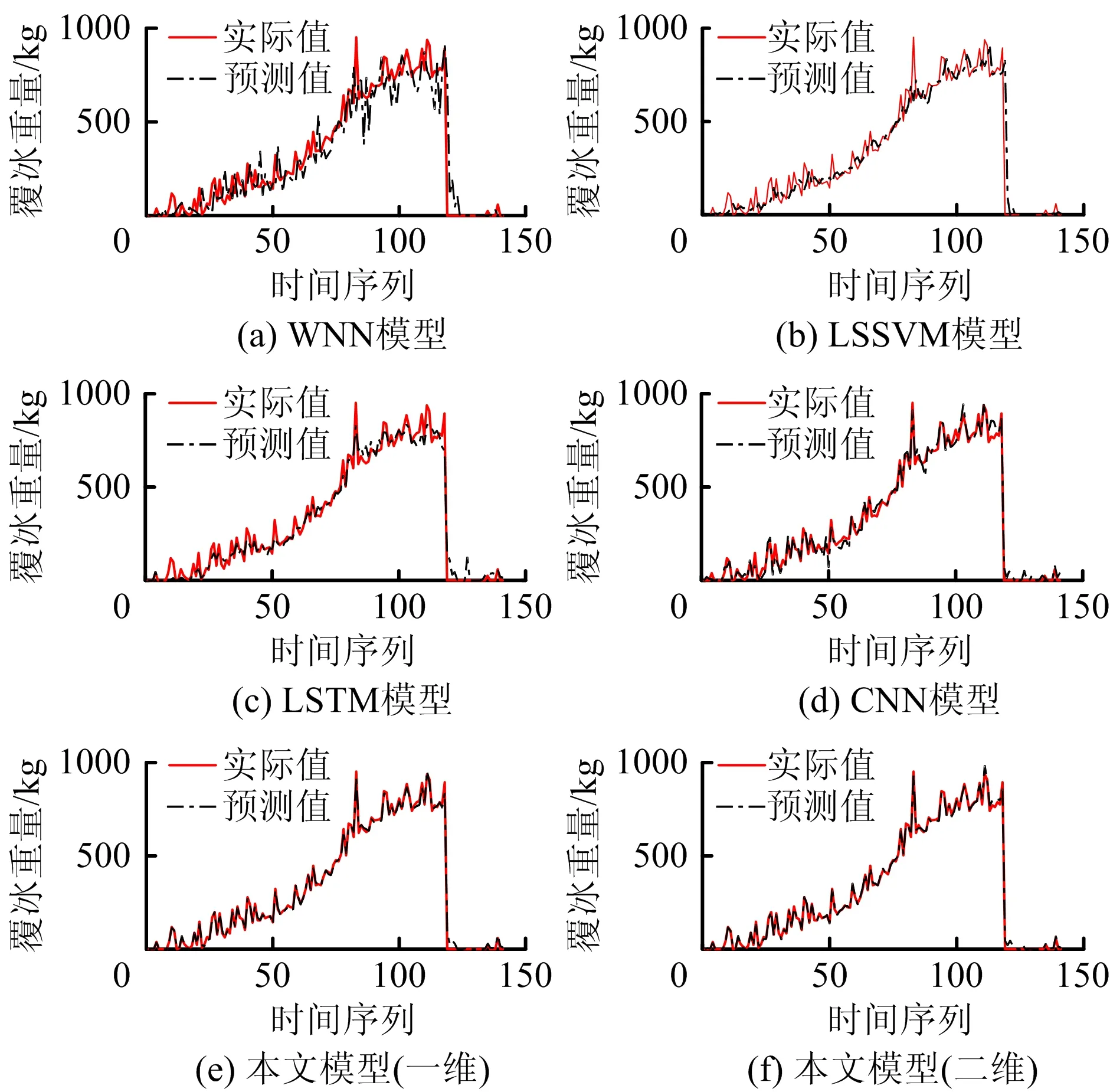
圖8 模型單步長預測結果對比Fig.8 Comparison on prediction results of different methods

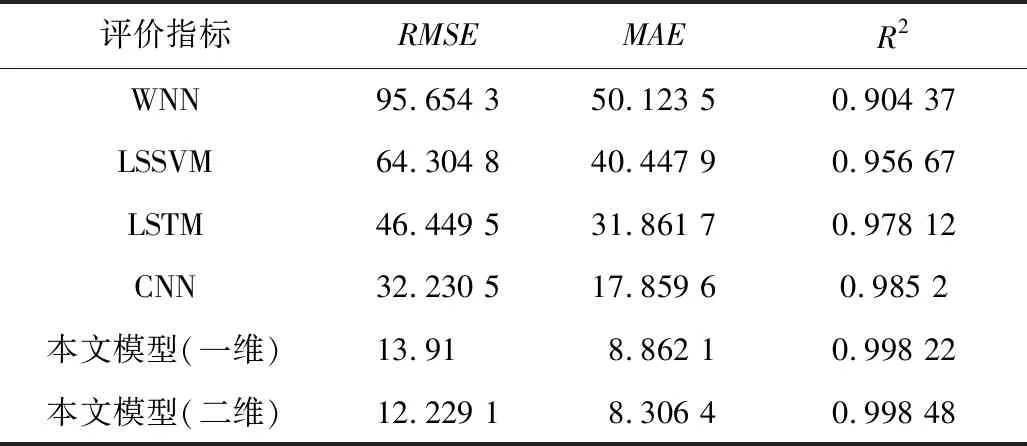
表2 單步長結果對比Table 2 Comparison of single step size results

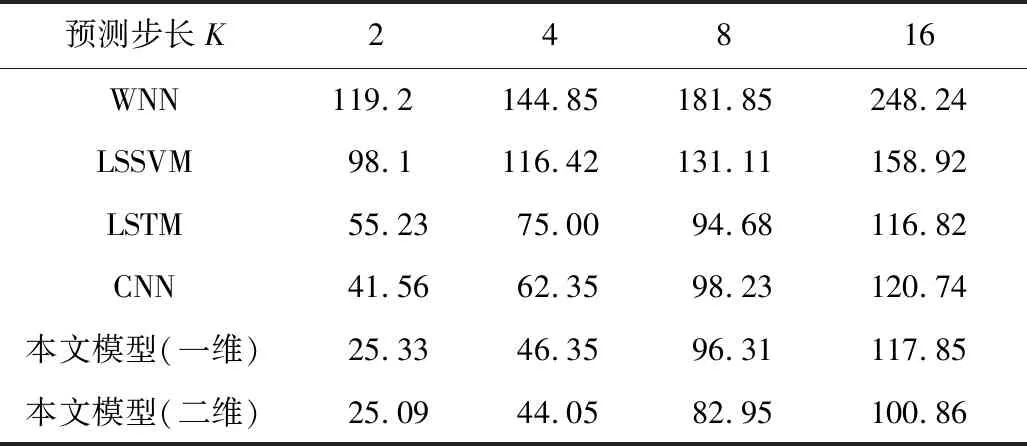
表3 多步長預測值RMSE對比Table 3 Comparison of multiple step size prediction value RMSE

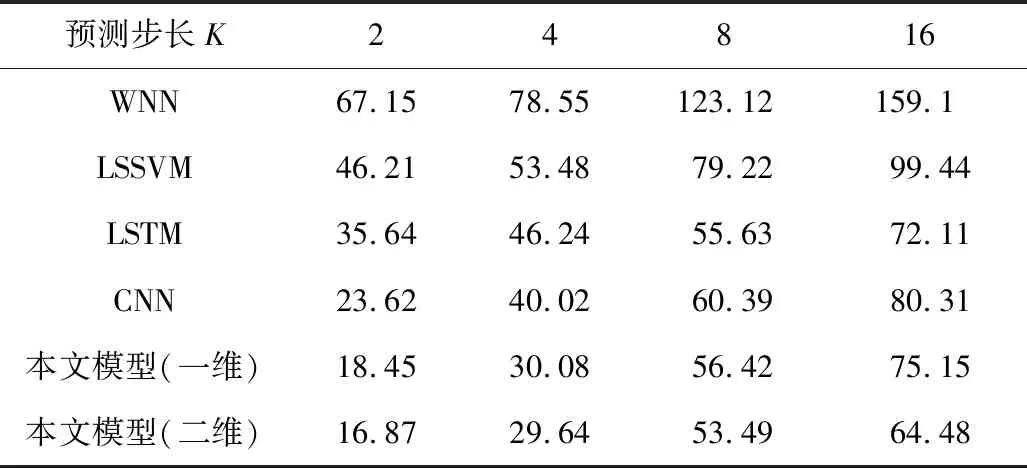
表4 多步長預測值MAE對比Table 4 Comparison of multi step predicted value MAE

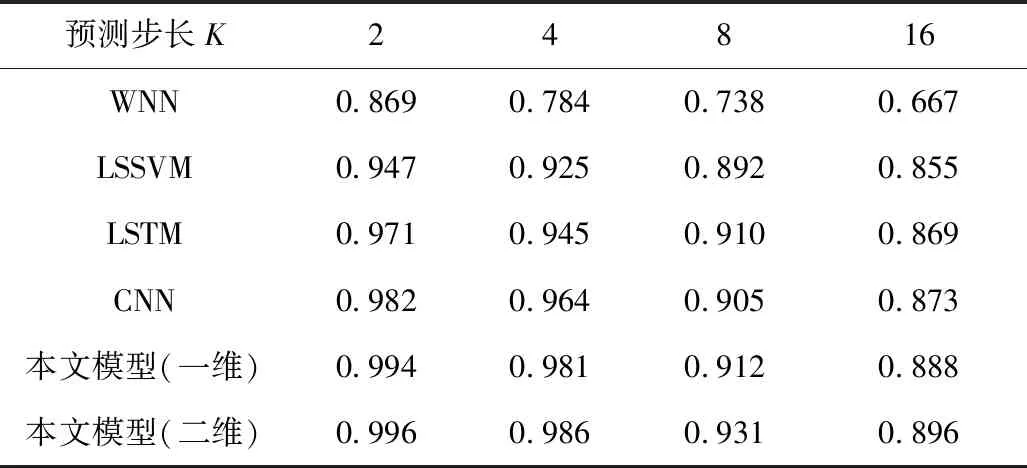
表5 多步長預測值R2對比 Table 5 Comparison of multiple step size prediction value R2

圖9 模型單步長絕對值誤差對比Fig.9 Comparison on absolute value error of single step size in model

當K=2,4時，對比表3～5，本文模型具有明顯優勢。然而當K=8,16時，本文模型(一維)并沒有什么優勢，由此利用卷積神經網絡的優勢，將一維數據構造為二維矩陣，對單步長預測和多步長預測精度有明顯的提升。可以看出，在大多數情況，本文預測模型優于其他模型，從而證明本文模型的可行性和優越性。

4 結論

1)架空輸電線路覆冰負荷與地理環境、宏觀氣象因子之間存在非常復雜的多層依賴關系，單純依靠氣象信息誤差大、精度低。本文將氣象數據與歷史覆冰相結合建立預測模型，通過實驗證明，本文所構建的預測模型安全性更高、可靠性更強，對單步長和多步長、平穩態和非平穩態覆冰過程都有著很好的預測效果，具有重要工程實踐意義。

2)架空輸電線路覆冰時間序列具有多尺度特性、非平穩性。如果對原始序列直接預測精度低，通過VMD將非平穩的隨機線路覆冰負荷序列數據自適應分解為若干個具有不同尺度特征的IMF分量，對每個分量分別預測，通過實驗分析，VMD分解能夠有效提高預測精度。

3)深度學習網絡具有淺層神經網絡沒有的優勢，可以更好地表示復雜的函數，而卷積神經網絡對二維數據的特征提取能力很強，因此本文利用這一特性將歷史覆冰數據重構為二維數據，進一步提高預測，然而深度學習參數的選擇只能通過經驗選擇，可解釋性差，未來可進一步開展研究。