基于改進權函數的探地雷達和無網格模擬檢測混凝土結構空洞缺陷工程中的數學問題

張冠軍，余 聰，黃 山，舒志樂，劉保縣，吳海寬*

（1.四川建筑職業技術學院，四川德陽 618000；2.成都農業科技職業學院，四川成都 611130；3.成都工業學院，四川成都 611730；4.西華大學應急管理學院，四川成都 610039）

1 研究現狀

無網格計算方法（也稱為無單元方法）最早出現于1977 年。無網格方法具有計算精度高、自適應能力強和靈活性高等特點[1]，這些方法包括光滑粒子流體動力學（SPH）方法[2]、擴散單元（DE）方法[3]、無網格伽遼金（EFG）方法[4]，單位有限元（PUFE）方法[5]、h-p 云方法[6]和再生核粒子（RKP）方法[7]。

在這些無網格方法中，EFG 方法是最流行的方法之一，并在許多工程領域中使用。通過前人的工作可以發現，基于不同權函數的無網格方法應用于不同的工程領域，但很少用于探地雷達無損檢測領域。因此，將基于改進法向權函數的無網格方法應用于探地雷達的無損檢測。在無網格法中引入了改進的權函數。權重函數可以提高無網格方法的計算速度和精度。采用無網格法，結合電磁波理論和透射吸收邊界條件，模擬了混凝土結構內部無損探地雷達探測到的損傷信號。

2 實驗和模擬方法

2.1 實驗和測試方法

混凝土結構空隙模型的設計示意圖和制作見圖1。模型由C30 混凝土制成，細骨料為砂，粗骨料由大米和石頭制成。水泥標記為32.5R。水泥：砂：礫石：水的比例=300:680:1260:160（所有單位均為kg/m3）。中空形狀由膠合板形成。為了確定空腔的位置，將試塊分為三層進行澆注。澆筑第一層以放置空腔模型的截面，澆筑第二層以淹沒空腔的中心截面，并在設計頂部澆筑第三層。澆筑后28 d 澆水和維護后，拆除模板。

圖1 混凝土結構空腔模型示意及制作圖（mm）

模型采用美國探地雷達SIR3000 探測，混凝土結構模型采用900 MHz 天線測量。在測線布置方面，當測線數量較大時，實際工程中測線過多會造成巨大工作量，不符合實際工程情況。當測線太少時，最終檢測結果的準確性會受到影響，無法準確反映內腔疾病的真實情況。可以看出，不同距離的測量線對測試有不同的影響。因此，綜合考慮，選擇43 條測線分別布置在坐標的X 和Y 方向，測線之間的距離為2.5 cm。檢測范圍為105 cm×105 cm，在模型上精確繪制測量線，為后續檢測測試做準備。測試方法使用距離模式。距離模式通過安裝在天線上的固定輪的旋轉來檢測，以觸發天線發射電磁波。在使用距離測量之前，需要校準車輪。校準后，可以精確測量車輪行駛的距離，從而有效定位目標。

2.2 改進的正態權函數

鑒于形狀函數的連續性受無網格方法中權函數的連續影響，選擇合適的權函數在無網格方法非常重要，可以顯著提高計算速度的精度和收斂性。

權重函數表示為兩點之間距離的函數，

其中ri=||x-xi||是x 和xi之前的距離

（1） 如果權函數是非奇異的，則權函數相對于坐標x，y，z 的偏導數可以通過以下方式發生，假設ωi（1）如果k 是一個正整數，則ωi有相對于x，y，z 的第次偏導數。

（2） 如果k 不是一個正整數, 但是k＞n/2，則ωi至少有n 關于x，y，z 的偏導數。

常見的標準函數如下

設t1=ρcosθ，t2=ρsinθ 則t12+t12+ρ2和ρ ∈（0，+∞），θ∈（0，2π）

則等式（4）可以寫成

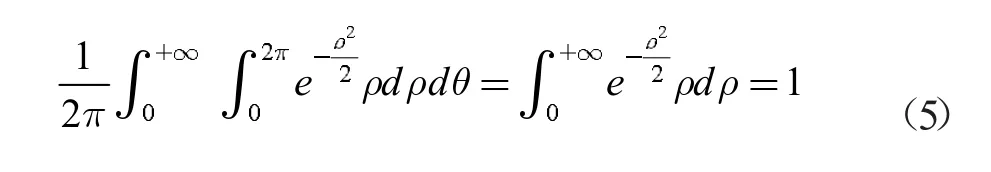
對數正態函數可以表示為

等式（6）是大于零的函數。

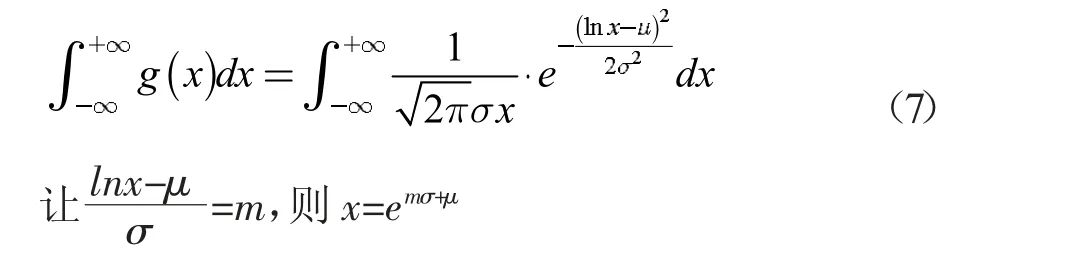
等式（7）可以通過將上述替換為

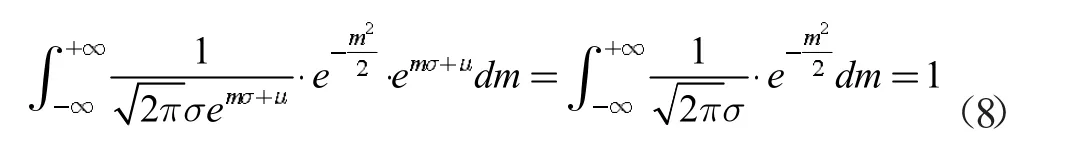
根據權函數的定義，對數正態函數可以用作權函數。設r=lnx-μ 則改進的法向權函數為

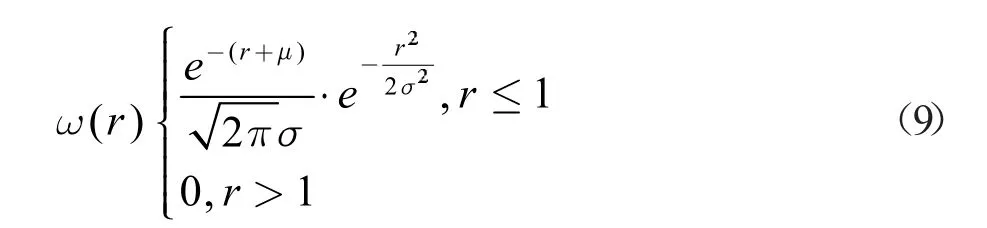
其中σ 和μ 根據正常函數定義。圖2 是改進的正常權函數的示意圖。可以看出，μ 在一定條件下，σ 的值盡可能小。

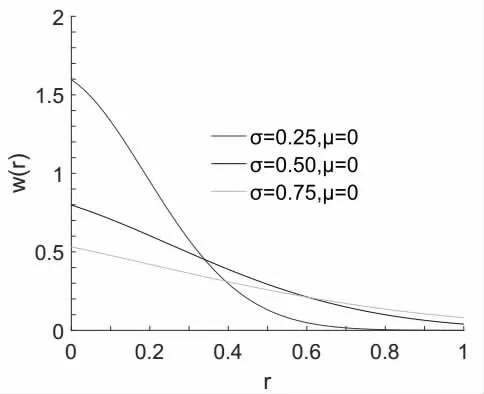
圖2 改進的權函數曲線

一般工程應用中常用的權函數包括指數權函數、高斯權函數、三次樣條權函數和正交樣條權函數。函數公式如下

（1） 指數權函數

（2） 三次樣條權函數

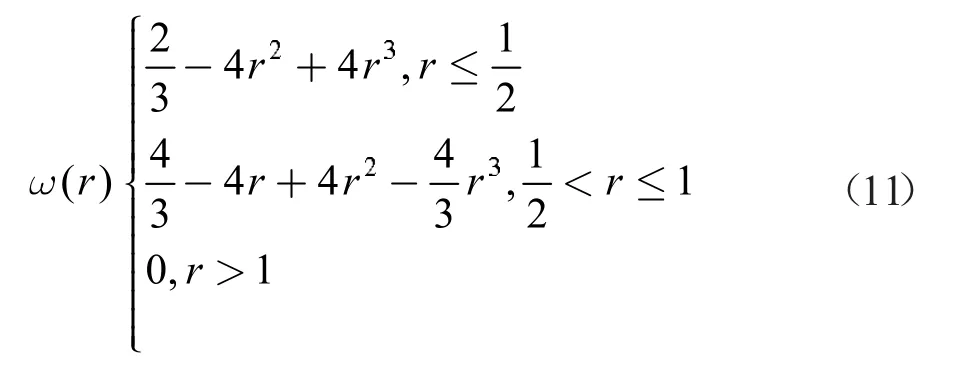
（3） 正交樣條權函數

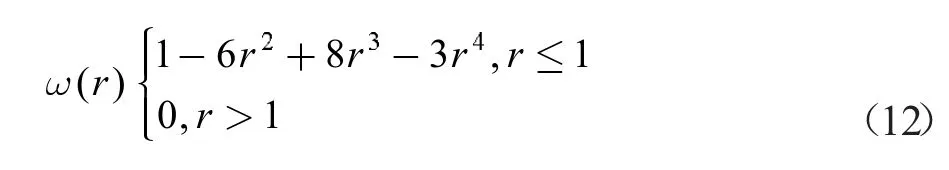
（4） 高斯權函數

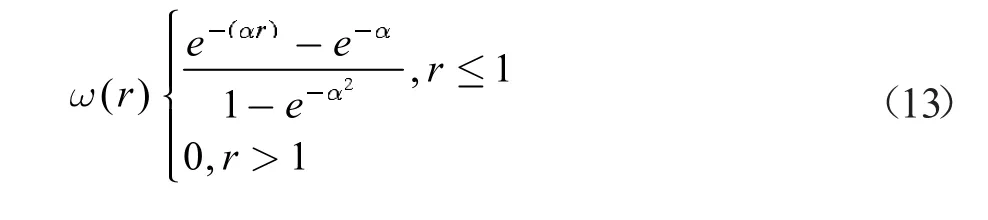
3 結果和分析

3.1 探地雷達探測結果

檢測結果的二維濾波圖像和三維切片圖像見圖3和圖4。

圖3 探地雷達檢測二維FIR 濾波圖像

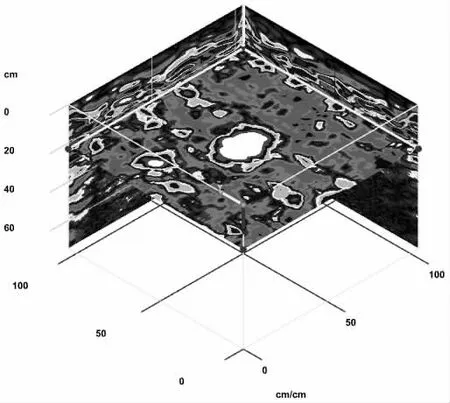
圖4 探地雷達探測的3D 切片圖像

3.2 模擬結果

數字模擬采取的空腔模型為1 m×0.5 m 的矩形，空腔為菱形。菱形腔的對角線長度為20 cm，中心點位于整個模型的中心。混凝土的相對介電常數為10，空腔中介質的相對介電常數為1，混凝土的電導率為0.005 s/m。背景網格間距為0.1 m×0.1 m，共設置100×50 個背景網格，高斯積分階數為4。使用MATLAB 軟件編制相應程序，模擬模型的無網格方法（圖5）和不同時間的波場強度。

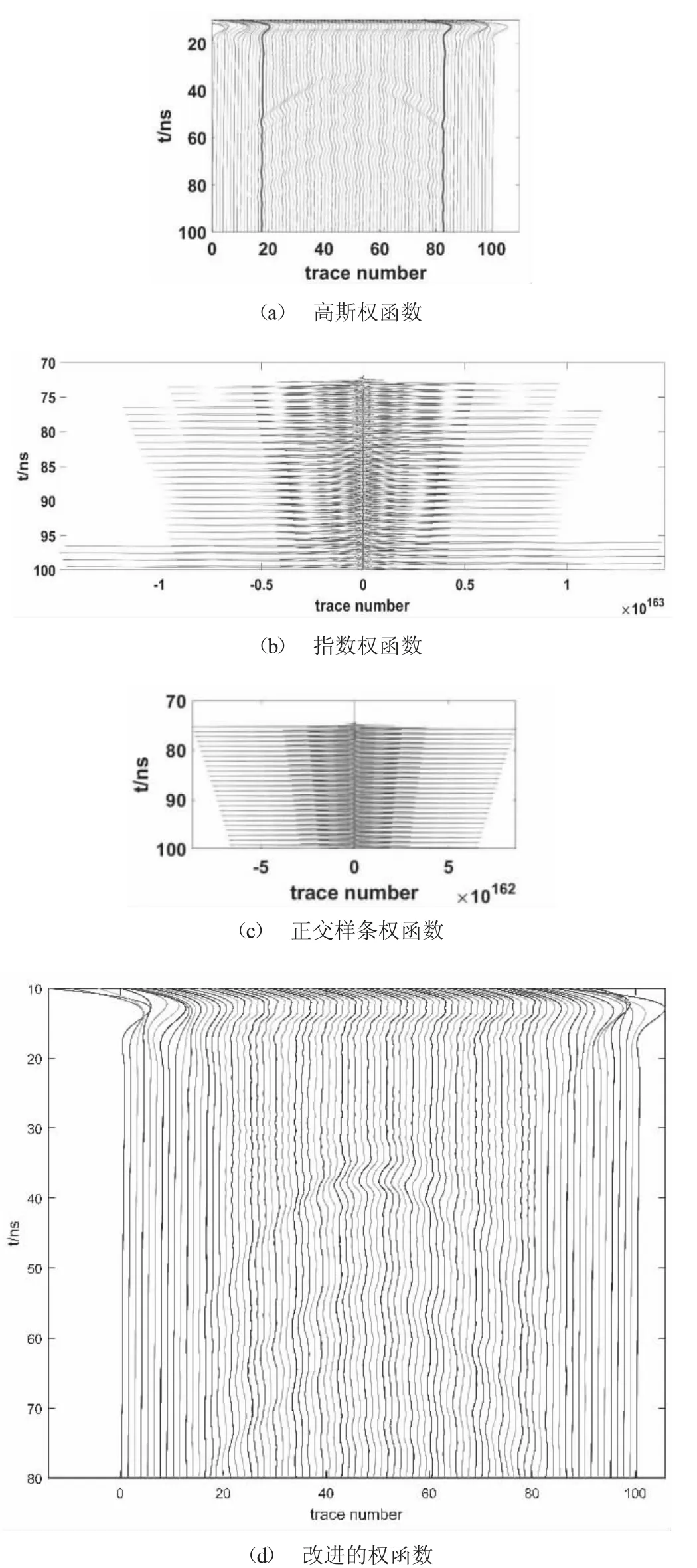
圖5 數值模擬示意圖

3.3 分析

在選擇合適的權函數時，應考慮權函數的收斂性和準確性，并減少計算工作量。

在靈敏度方面，改進的權函數、指數權函數和高斯權函數隨參數變化顯著，表明它們對參數高度敏感。不同的參數選擇導致不同的權重。因此，可以通過調整參數使權重函數更具適應性。三次樣條函數的權函數類似于正交樣條的權函數。由于三次樣條的權函數和正交樣條函數的權函數不包括附加參數，因此不會出現參數敏感性問題。因此，三次樣條的權函數和正交樣條權函數的擬合度較差。

在收斂性方面，改進的權函數、指數權函數和高斯權函數具有與參數選擇相關的收斂性。隨著σ 的減小，改進權函數的收斂速度加快，收斂效果良好。隨著α 的增加，指數權函數和高斯權函數的收斂速度逐漸加快，收斂效果逐漸改善。然而，高斯權函數只有在α 大于1 后才逐漸顯示出改進的收斂性能。三次樣條和正交樣條權函數的收斂性是固定的，因為沒有附加參數，并且三次樣條權函數的聚合性優于正交樣條線權函數。

在相同CPU 和計算機的程序計算方面，每個權重函數的計算時間明顯不同。其中，改進權函數、高斯權函數、指數權函數、正交樣條權函數和三次樣條權函數的計算時間分別為0.106 733 s、0.112 047 s、0.112 874 s、0.130 706 s 和0.114 216 s。計算時間順序為：改進權函數<高斯權函數<指數權函數<三次樣條權函數<正交樣條權函數。可以看出，改進權函數排名最低，而正交樣條權函數排名最高。

從收斂性、靈敏度和計算時間的分析可以發現，改進權函數比其他權函數具有一定的優勢，包括靈敏度更高、收斂更明顯和計算時間相對較小。因此，將改進權函數應用于無網格方法可以提高模擬的收斂性和精度，并減少計算時間。

圖3 和圖4 顯示了探地雷達的二維和三維檢測結果。2D 檢測結果表明，X 方向和y 方向FIR 濾波圖像。如圖3 所示，不同方向的結果也不同。雙曲線圖像由x 方向上的檢測結果表示。在y 方向上檢測到黑色區域。三維檢測結果表明，一定深度切片圖像的探地雷達檢測。混凝土結構的內部缺陷反映在圖4 中水平面的白色區域中。

混凝土結構內部缺陷的無網格法模擬結果見圖5。對于空腔缺陷，弧形曲線反映在圖中。該弧形曲線兩側的能量較弱，因此曲線逐漸變薄。在中間，能量最強，曲線最厚。由于吸收不良，在雜波中會出現一些圖形。模擬不同時間的波場強度。0-20 ns、0-40 ns、0-60 ns、0-80 ns、0-100 ns 表示電磁波場逐漸增大的規律。從模擬結果可以看出，電磁波在傳輸過程中波場強度明顯增強，而在缺陷外部時波場強度減弱。

4 結論

通過對權函數、無網格法和實驗的分析，得出以下結論。

（1） 引入了一種新的改進權函數，并證明了其適用性。在參數選擇方面，μ 選擇了某個值，同時σ值較小。在收斂性、精度和計算時間消耗方面，改進權函數比其他權函數具有更多的優勢。

（2） 將改進權函數應用于無網格計算方法。結果表明，基于改進權函數的無網格法正演模擬與實驗觀測基本一致。正演模擬程序具有良好的適用性，并說明了理論分析的正確性。

（3） 波場強度的模擬結果反映了探地雷達在混凝土缺陷中電磁波傳播的基本規律。當電磁波在傳輸過程中，波場強度明顯增強，而當電磁波位于缺陷外部時波場強度減弱。