點源反演問題的神經網絡方法研究

張平，孟品超，尹偉石

（長春理工大學 數學與統計學院，長春 130022）

反源問題是指通過遠場數據識別未知點源的某些參數，如位置和強度等，目前已成為醫學成像、環境污染、層析成像和天線合成等領域中的重要問題［1-2］。

研究單頻反源問題的一個難點是解的不唯一性，為此，人們通常需要對源施加額外的約束［3］。文獻［4］和其中的參考文獻給出了反源問題的穩定性估計。目前求解單頻反源問題的方法主要有迭代法、直接采樣方法和貝葉斯方法等［5-6］。傳統方法在求解反演點源位置的問題時往往會限制點源之間距離［7-8］。此外，對于單頻的反源問題，在許多實際應用中往往只能在有限孔徑情況下觀測點源位置［9］。

近年來，神經網絡方法發展迅猛，能夠彌補信息的缺失，對非線性映射有著較好的逼近效果，一些學者將其用以求解反問題［10-12］。本文針對單頻聲波反源問題，構建基于神經網絡和門控思想的點源位置參數反演模型，利用單頻遠場數據，確定點源位置信息。

1 聲波反源問題

考慮在如下Helmholtz系統中通過遠場模式u∞反演點源S的問題：

其中，δ表示Dirac分布，且N表示單極源的個數，為正整數；zj是單極源S的位置，這里，點源位置zj是互不相同的；λj表示單極源的強度，是一個標量。反源問題是：給定單極源S的強度和固定頻率的遠場數據u∞，確定單極源S的位置。

2 神經網絡模型

建立求解均勻介質中固定頻率聲波點源位置反演問題的神經網絡模型。首先給出以下假設和定義：

假 設1：觀測方向d=(c os(α),sin(α))，觀 測角α均勻分布于觀測孔徑(α1,α2)，即：

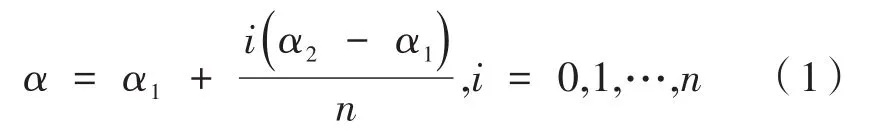
其中，n為觀測方向個數。

因此，給定n個觀測方向，得到遠場數據：X=(x1,x2,...,xn)。為方便計算，將每個遠場數據xt=at+i·bt改寫成xt=(at,bt)T,t=1,2,...,n。這里i表示虛數單位。

定義1：假設點源的位置有如下形式：

其中，M=2N表示位置參數的個數。于是，可將利用均勻介質中固定頻率的遠場數據u∞反演點源位置zj轉化為反演位置參數y=(y1,y2,…,yM)的問題。

定義 2：令A=(aij)為n×m維的矩陣，且B=(bij)為一個p×m矩陣，則矩陣運算[A;B]表示矩陣拼接：

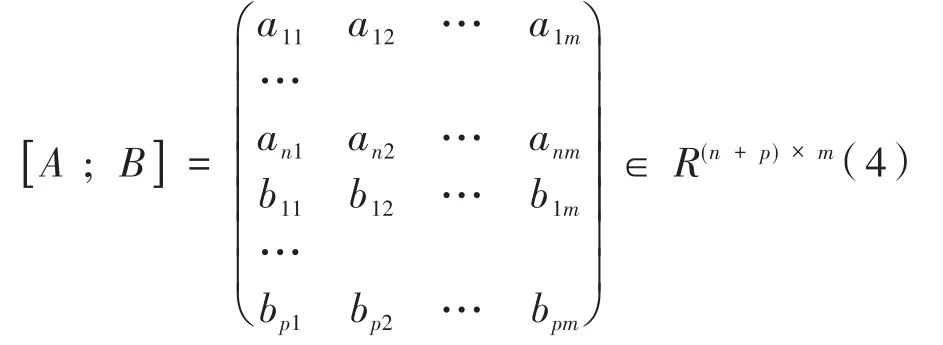
定義3：令A=(aij)，B=(bij)為n×m維矩陣，則定義：

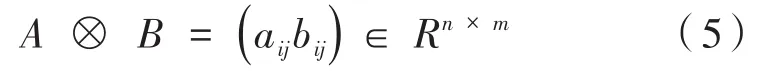
定義4：令F為激活函數，A=(a1,a2,…,am)T為m維向量，則F(A)為一個m維向量：

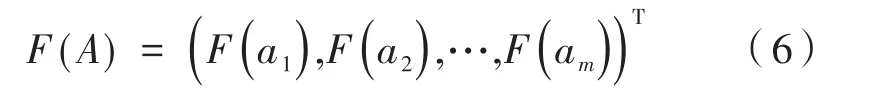
下面利用可在時間維度上傳播信息且具有“記憶”功能的神經網絡，構建位置參數反演模型，反演點源的位置參數y=(y1,y2,…,yM)。

2.1 構建模型

構建一個位置參數反演模型，其結構如圖1所示，分為特征提取和參數反演兩部分。

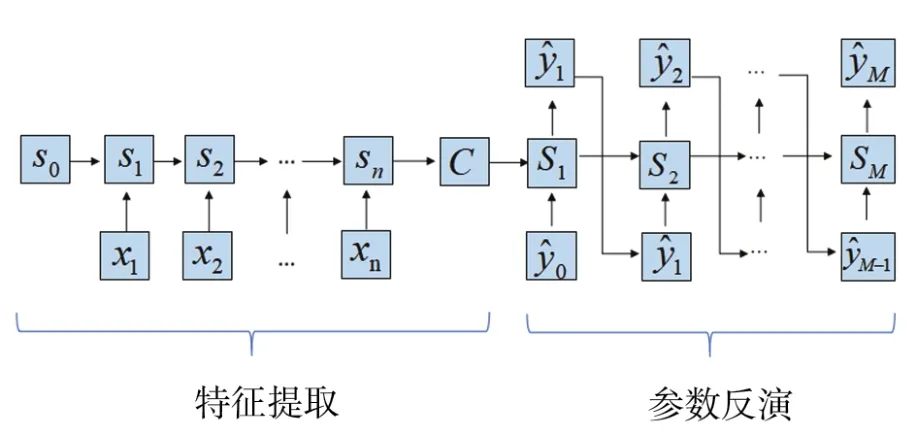
圖1 位置參數反演模型

用st表示t時刻提取的遠場特征，t=1,2,...,n，隨機初始化s0。構造映射F:Rm×2×R2→Rm×2，對st-1和xt進行特征提取，并將其記作st=F(st-1,xt),t=1,2,…,n。其中st=(ht,ct),ht=(h1t,h2t,…,hmt)T，ct=(c1t,c2t,…,cmt)T，ht為t時的短時遠場特征，ct為t時的長期遠場特征，經過n個時間步后可得X的遠場特征：C=sn。

圖2給出了映射F中變量之間的關系，為方便描述，本文令偏置為零向量，即b=(0 ,0,…,0)T。

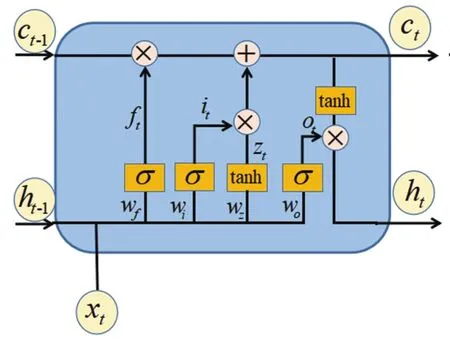
圖2 映射F中的變量關系

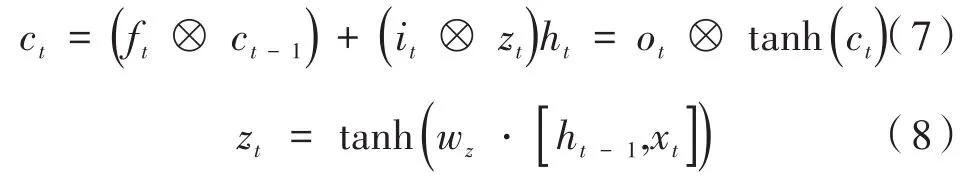
其中，ft=σ(wf·[ht-1,xt])為遺忘門，決定保留多少ct-1中的信息并使其繼續傳播。類似的，輸入門it=σ(wi·[ht-1,xt]),決定zt中有多少信息保存到長期遠場特征ct，輸出門ot=σ(wo·[ht-1,xt]),決定ct中有多少信息輸出到ht。tanh表示雙曲正切函數，σ為Sigmoid函數。wf,wi,wo,wz∈Rm×(m+2)分別表示遺忘門、輸入門、輸出門和候選向量的權重，[ht-1,xt]∈Rm+2，ot,ft,it,zt∈Rm。

至此，模型提取了遠場特征C=sn=(hn,cn)，下面進行參數反演。

與特征提取階段相似，在圖1參數反演階段，用ST=(HT,CT),表示T時的參數特征，T=1,2,…,M，其中HT∈Rm為短時參數特征，CT∈Rm為長期遠場特征。初始化0=0，構造映射L:Rm×2×R→Rm×2，將ST-1=(HT-1,CT-1)和位置參數T-1映射成，其計算過程如下：

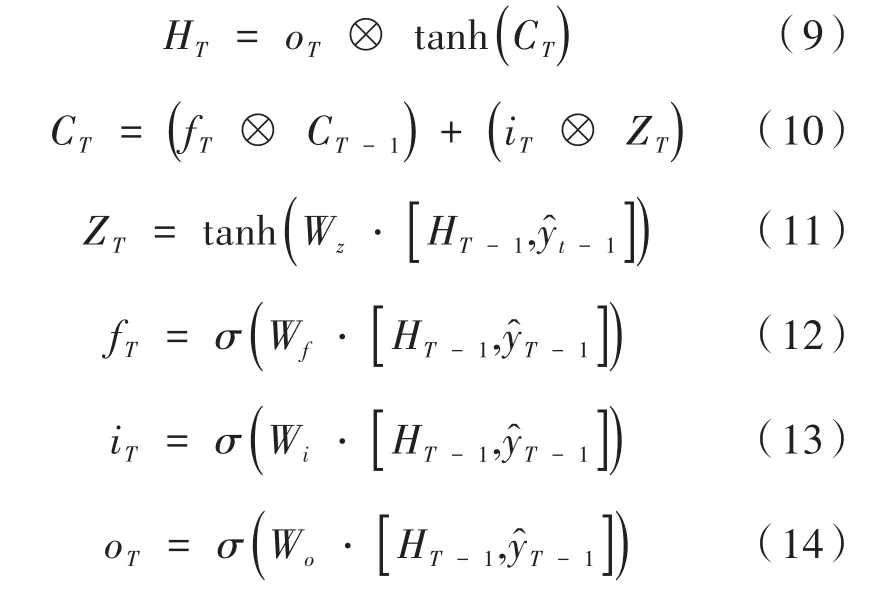
因為HT∈Rm，且∈R，因此本文通過一個輸出維度為1的全連接將HT反演為第T個位置參數=WDT·HT，其中WD∈Rm為與時間步T對應的全連接權重。經過M個時間步，可反演出全部M個位置參數。

2.2 模型參數更新方法

由于每個位置參數∈R，即“連續”，因此本文使用均方誤差作為損失函數E。

定義 3：令Yj為模型的真實輸出，為模型的預測輸出，定義損失函數為：

式中，J為樣本總數。

更新模型就是更新模型中的權重和偏置，用W表示模型中的權重wo,wf,wi,wz,Wo,Wf,Wi,Wz,WD，這里隨機初始化權重W(0)，然后利用Adam算法更新權重W(l)，l=1,2,…,n。更新規則如下：

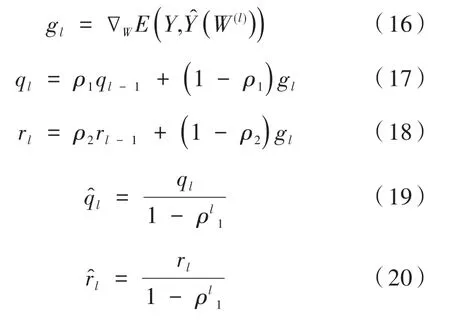
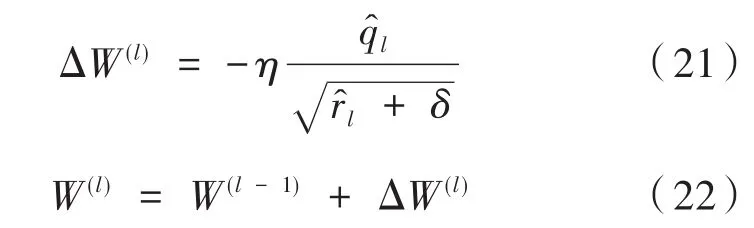
其中，gl為損失函數相對于權重W的梯度矩陣；ql和rl分別為gl的一階和二階有偏矩估計，且q0,r0均初始化為零向量；ρ1，ρ2∈ [0,1)為矩估計的指數衰減速率；和l分別為修正的一階和二階矩估計；η為學習率；δ為數值穩定常數。本文令ρ1=0.9，ρ2=0.999，η=10-2，注意在計算ΔW(l)時需對矩陣l和l逐個元素執行相應運算，即。

至此，本文構建了反演點源位置參數的神經網絡模型，下面進行數值實驗說明該模型的有效性。

3 數值實驗

通過數值例子說明位置參數反演模型能夠解決有限孔徑和點源之間距離較小等限制的反源問題。

3.1 實驗設置

對于點源位置表達式：

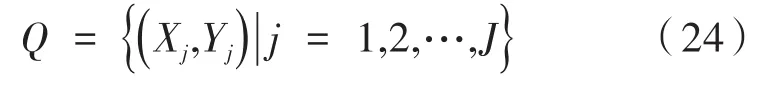
將數據集劃分為訓練集與測試集，其中測試集中樣本數據量固定為l=100，在測試集中隨機選取測試樣本。在模型訓練過程中進行批量訓練，批量大小滿足1＜v＜J。

表1給出了模型所用超參數，這些參數是通過多次實驗得到的。

表1 模型超參數

3.2 模型的魯棒性

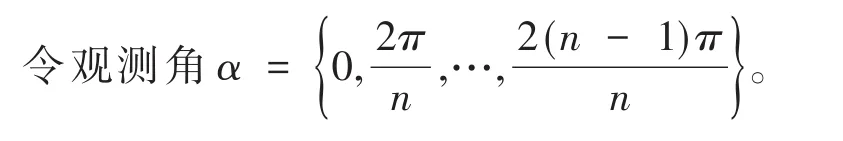
實驗一：遠場數據不加噪聲。

點源個數N=2時，令n=8，10和12，遠場數據無噪聲。為了比較位置反演的精度，表2列出了精確和預測的數據。反演位置參數的均方誤差如表3所示。

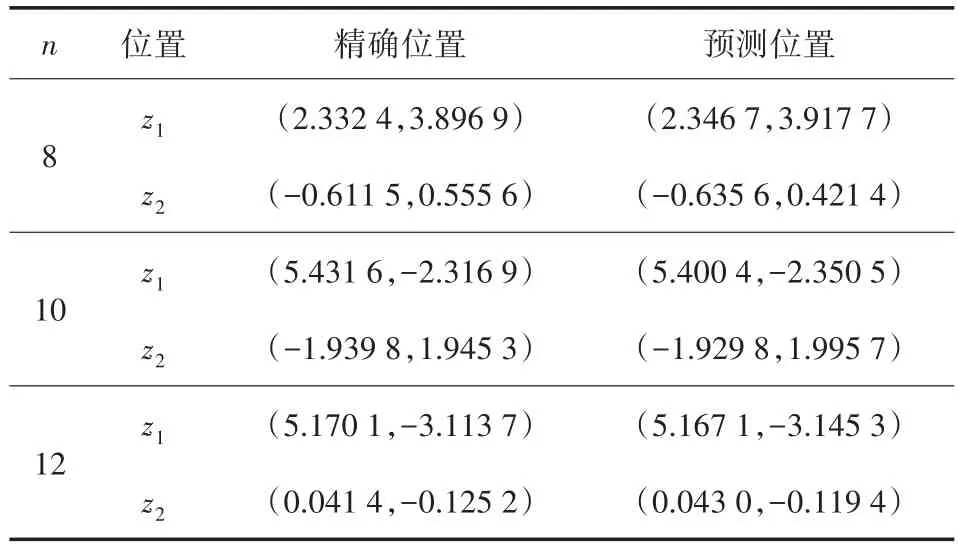
表2 兩個點源的位置反演效果

表3 參數反演的均方誤差

表2和表3說明：隨著觀測方向的增加，獲得的遠場信息增多，損失函數減小，點源位置的反演效果提升。

點源個數N=3時，令n=15，16和 17，遠場數據無噪聲。為了比較位置反演的精度，表4列出了精確和預測的數據。反演位置參數的均方誤差如表5所示。

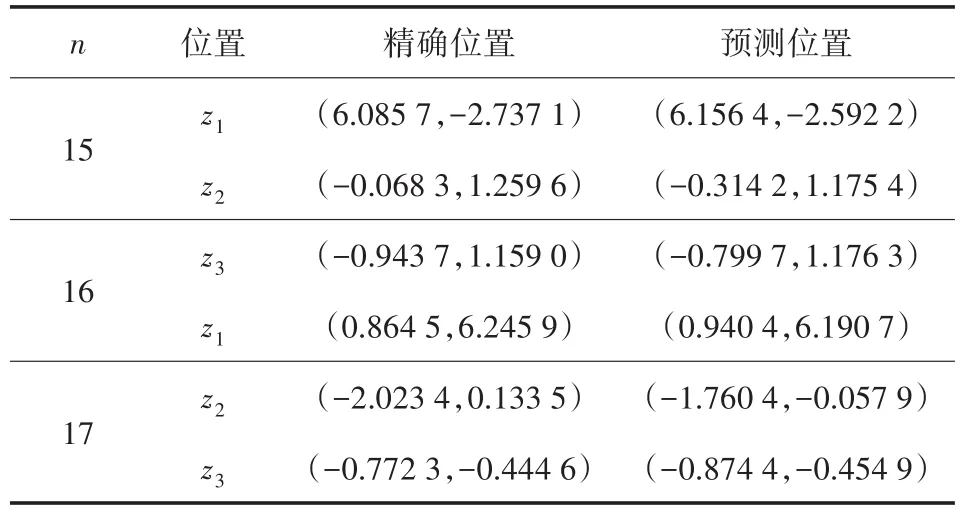
表4 三個點源的位置反演效果

表5 參數反演的均方誤差

表4和表5同樣說明：隨著觀測方向的增加，獲得的遠場信息增多，損失函數減小，點源位置的反演效果提升。

實驗二：遠場數據加噪聲。

在實際測量中遠場數據經常含有一定的測量誤差，為說明模型在此種情形下的反演效果，本實驗以兩個點源為例，取觀測點n=12，遠場數據含不同水平的高斯噪聲ε。為了比較位置反演的精度，表6列出了精確和預測的數據。反演位置參數的均方誤差如表7所示。

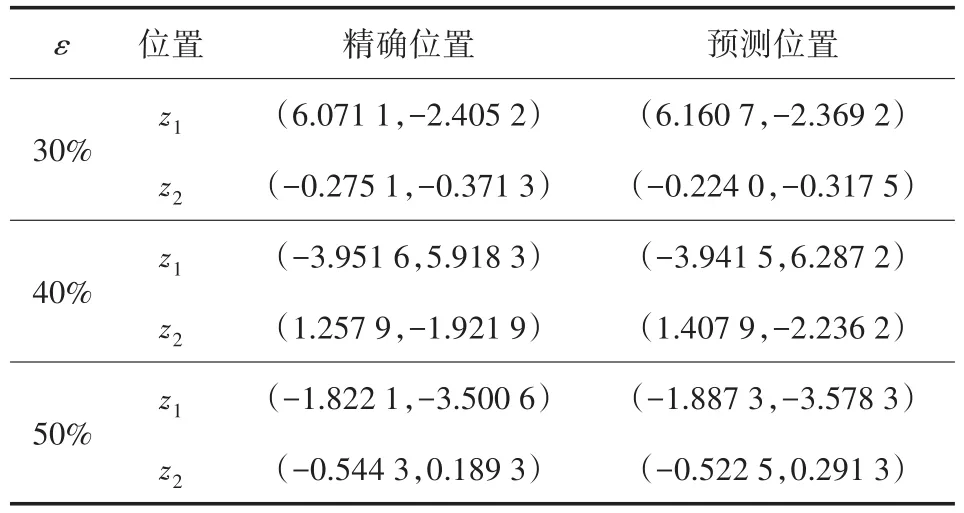
表6 遠場數據加噪聲的點源位置反演效果

表7 參數反演的均方誤差

由表6和表7可知，在使用含有乘性高斯噪聲的測量數據反演點源位置參數時，模型可較好地反演點源位置參數，這是因為該方法使用含測量誤差的遠場數據與真實位置參數進行訓練，逼近了二者之間的映射，進而降低了測量誤差對反演效果的影響，該實驗說明模型具有一定的魯棒性。

3.3 有限觀測孔徑

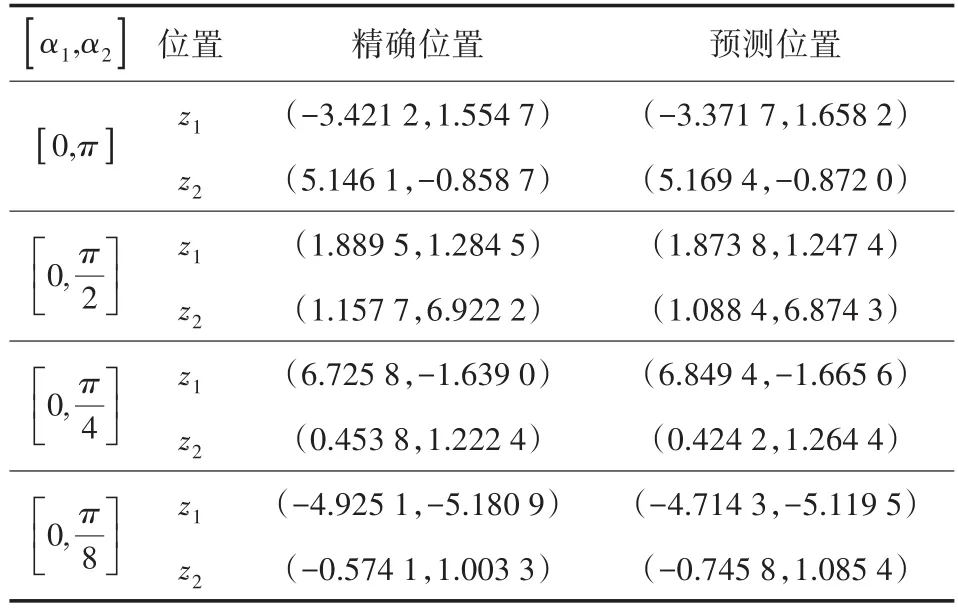
表8 有限觀測孔徑下的點源位置反演效果

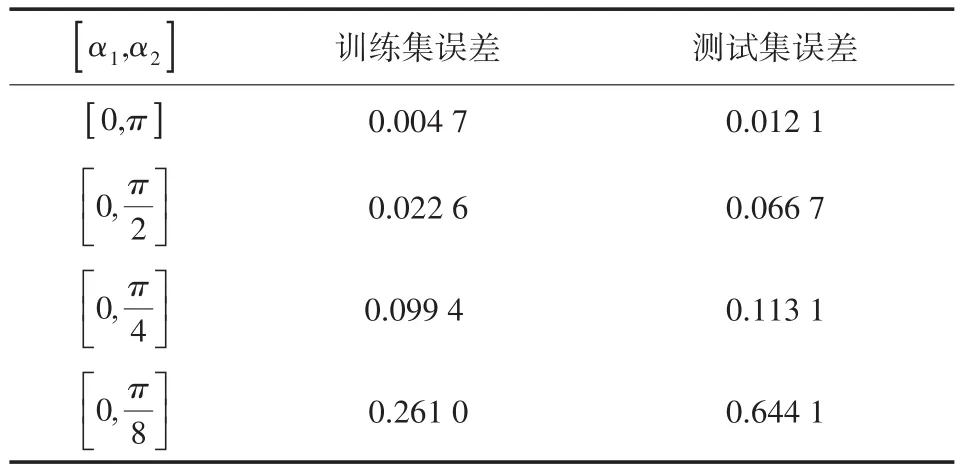
表9 參數反演的均方誤差

由表8和表9可知：當觀測方向數目不變時，隨著觀測孔徑的逐步縮小，觀測方向間的夾角減小，觀測到的遠場數據相似度上升，導致從遠場數據中獲得的點源位置信息減弱，使得位置參數的反演誤差增大，反演效果下降。

3.4 點源間距有限

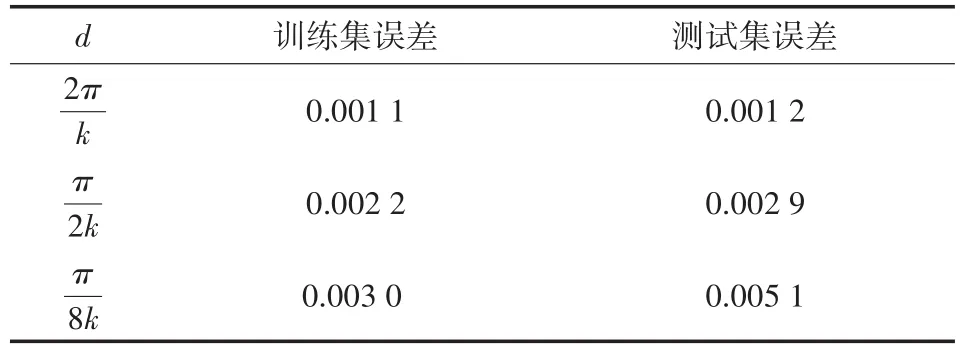
表10 參數反演的均方誤差

4 結論

本文針對單頻遠場信息反演點源位置的聲波反源問題，構建了基于神經網絡和門控思想的位置參數反演模型，反演點源的位置。實驗結果表明該模型反演效果良好，在噪聲干擾下模型具有一定的魯棒性和泛化性，點源之間距離的大小對該模型的反演結果影響較為微弱。三維立體空間中移動點源位置的反演，是更有現實意義的問題，而近場問題涉及到精確度與更微觀層面的問題，這將是下一步的工作。