函數性質中的數學抽象在問題解決與設計中的應用

201299 上海市新川中學 姚志青

2017年版《普通高中數學課程標準》給出了普通高中數學學科的核心素養要求，包括數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析六個方面.數學發展所依賴的思想在本質上有三個，即抽象、推理、模型，其中抽象是核心.數學抽象作為一種數學思想滲透在數學學科的各個知識點之中，筆者對如何在函數性質中體現數學抽象以及如何應用數學抽象進行問題設計展開實踐與研究.

一、 數學抽象在函數性質中的體現

函數是貫穿高中數學的一條主線，數學抽象在函數問題中的應用非常廣泛，以2021年上海高考的數學壓軸題為例.

原題如果對于任意的x1,x2∈R，當x1-x2∈S時，恒有f(x1)-f(x2)∈S成立，則稱f(x)是S關聯.

(1)判斷并證明f(x)=2x-1是否是[0,+∞)關聯？是否是[0,1]關聯？

(2)已知f(x)是{3}關聯，且x∈[0,3)時，f(x)=x2-2x，解不等式2≤f(x)≤3.

(3)求證：“f(x)是{1}關聯，且是[0,+∞)關聯”的充要條件是“f(x)是[1,2]關聯”.

這個問題是一個函數的定義型問題，它定義了“f(x)是集合S關聯的概念”，通過函數性質的應用考查學生的數學核心素養.函數性質的應用體現了其源于教材中的形式，需要將函數的性質在文字語言、符號語言、圖像表述三個方面進行內化，以理解函數性質的本質特征.這個內化的過程可以體現在數學抽象方面，所謂數學抽象就是能夠根據一類數學對象抽取或歸納出其本質特征的思維過程.筆者結合上述具體的步驟，分析問題中涉及數學抽象的三個方面.

小問(1)解：由f(x)=2x-1，得f(x1)-f(x2)=2(x1-x2).

當x1-x2∈[0，+∞)時，f(x1)-f(x2)∈[0,+∞)，所以f(x)是[0,+∞)關聯；當x1-x2∈[0,1]時，f(x1)-f(x2)∈[0,2]，所以f(x)不是[0,1]關聯.

(一)數學抽象需要類比抽象

由題中f(x1)-f(x2)的形式容易類比聯想到教材中的形式，在函數單調性中，通過f(x1)-f(x2)來作差比較f(x1)，f(x2)大小，從而確定f(x)的單調性.解題過程中“由f(x)=2x-1得到f(x1)-f(x2)=2(x1-x2)，則當x1-x2∈[0，+∞)時，f(x1)-f(x2)∈[0,+∞)”的本質就是“當x1≥x2時，都有f(x1)≥f(x2)”，類比聯想到函數的單調遞增的性質(非嚴格單調)，所以可以通過類比的方法抽象得到f(x1),f(x2)的性質.類比抽象就是通過類比的方法抽象出數學對象的形式或性質，它包括兩個方面，一個是類比，一個是抽象.類比本身是非常重要的數學思想方法，數學中的類比是基于對兩類數學對象的共性比較得出它們可能具有的其他形式或者性質的方法.

小問(2)解：f(x)是{3}關聯，所以當x1-x2=3時，恒有f(x1)-f(x2)=3成立.

由f(x1)-f(x2)=x1-x2，得f(x1)-x1=f(x2)-x2，令F(x)=f(x)-x，有F(x1)=F(x2)，得到F(x2+3)=F(x2)，即對任意x∈R，都有F(x+3)=F(x).

故F(x)是一個周期為3的函數，且x∈[0,3)時，F(x)=x2-3x.

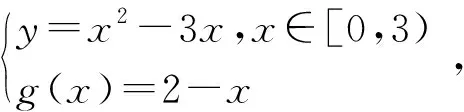
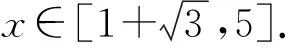
圖1

(二)數學抽象需要表征抽象

表征抽象就是以數學對象的呈現特征抽象構建出其形象化的特征結構.譬如由f(x1)-x1=f(x2)-x2的呈現特征，令F(x)=f(x)-x，為使f(x)-x的性質表征更加明顯，需要抽象構建出函數.解不等式2-x≤F(x)≤3-x的過程中，代數方法解決不等式問題比較復雜，利用數形結合的思想，可以用幾何圖像解決不等式問題，作出F(x)=x2-3x，g(x)=2-x，h(x)=3-x的圖像滿足F(x)在g(x)，h(x)之間的部分.對于表征抽象而言，關鍵在于結構特征的研究和歸納表述.對于同一個問題，表征抽象的觀察點不同，抽象得到的性質特征也會不同，譬如上述“當x1-x2=3時，恒有f(x1)-f(x2)=3成立”還可以抽象到“對任意的實數x∈R，恒有f(x+3)=f(x)+3成立”.

小問(3)解：

必要性：已知f(x)是{1}關聯，且是[0,+∞)關聯，

由f(x)是{1}關聯知f(x+1)-f(x)=1，即f(x+1)=f(x)+1，

由f(x)是[0,+∞)關聯,可知對任意x1-x2≥0，都有f(x1)-f(x2)≥0，即x1≥x2時，都有f(x1)≥f(x2)，所以，當x1-x2≥1時,x1≥x2+1,f(x1)≥f(x2+1),則有f(x1)≥f(x2)+1，f(x1)-f(x2)≥1.

當x1-x2≤2時，x1≤x2+2，有f(x1)≤f(x2+2)，則f(x1)≤f(x2+1)+1=f(x2)+2，f(x1)-f(x2)≤2.

因此，當x1-x2∈[1,2]時，都有f(x1)-f(x2)∈[1,2]，即f(x)是[1,2]關聯.

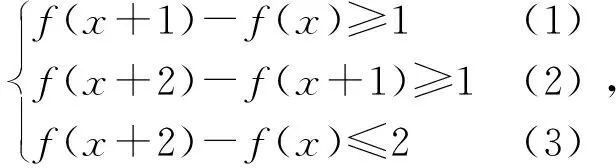
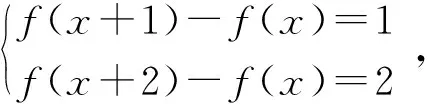
(三)數學抽象需要強、弱抽象

上述解題過程中將“f(x)是{1}關聯推出對任意的x1-x2=1，都有f(x1)-f(x2)=1”理解為當自變量相差1的時候都有相應的函數值也相差1，這樣的表述雖然弱化了對于定義描述的嚴謹性，但便于記憶表述.在應用過程中，又可以進一步加強為“對于任意的實數x，都有f(x+1)-f(x)=1”，這樣的描述是嚴謹的，而且便于理解表述.在概念教學中，數學抽象需要體現出不拘于形式的內化理解，這個內化理解根據實際情況的需要可以對研究對象進行弱化或強化的表述，也就是強抽象和弱抽象.滬教版新教材中關于增函數的定義為：“對于定義在D上的函數y=f(x)，設區間I是D的一個子集，對于區間I上的任意給定的兩個自變量的值x1,x2，當x10都有f(x+ε)>f(x)成立，則稱函數f(x)在區間I上為嚴格增函數”.用強抽象可以將上述圖形特征抽象為“函數f(x)圖像上的任意兩個不同的點，都有右邊的點高于左邊的點，則函數f(x)圖像為嚴格增函數圖像”.強抽象即通過在原型中引入新特征，使原型內涵增加，結構變強，從數學對象的關鍵屬性或特征中強化其特征屬性.

二、 應用數學抽象進行問題設計

從顯性來看，數學抽象是學生在觀察、思考、表達三個方面的能力，通過數學抽象進行問題設計是幫助學生實現問題解決和提升數學抽象能力的有效途徑.在高三函數性質的復習課中，根據數學學科核心素養的培養要求，筆者對如何通過數學抽象進行問題設計展開教學實踐的研究和分析(如圖2所示).

圖2

問題設計1對于任意的x1,x2∈R，當x1-x2∈S時，恒有f(x1)-f(x2)∈S成立，則稱f(x)是S關聯.求證:如果f(x)是{1}關聯，那么f(x)是{2}關聯.

解題反饋1學生解題情況統計結果顯示，參加解題的十位學生都不能給出完整的證明過程，但是證明過程中的第一步基本都能表述出來，即寫到如下證明步驟后證明思路就戛然而止.

解：由f(x)是{1}關聯，則對任意的x1,x2∈R，當x1-x2=1時，都有f(x1)-f(x2)=1.

解題難點分析：由“對任意的x1,x2∈R，當x1-x2=1時，都有f(x1)-f(x2)=1”推理得到“對任意的x1,x2∈R，當x1-x2=2時，都有f(x1)-f(x2)=2”的邏輯關系缺乏直觀想象，而且推出關系的表述存在較大困難.在教材中，經常用一個變量x的特征形式來表示函數f(x)的性質，學生對于理解x1-x2=1中兩個變量x1,x2之間的關系存在一定的困難.

難點突破策略：通過數學抽象，在保持函數性質不變的前提下，可以將問題抽象轉化為熟悉的形式.譬如，將“對任意的x1-x2=1，都有f(x1)-f(x2)=1”進行適當的強、弱抽象.通過弱抽象表述為“當自變量增大1個單位時，函數值增大1個單位”，通過強抽象表述為“對任意的x∈R,都有f(x+1)-f(x)=1”.通過數學抽象之后，將問題進行再設計.

問題設計2對于任意的x1,x2∈R，當x1-x2∈S時，恒有f(x1)-f(x2)∈S成立，則稱f(x)是S關聯.

(1)求證：如果f(x)是{1}關聯，那么對任意的x∈R，都有f(x+1)-f(x)=1.

(2)求證：如果f(x)是{1}關聯，那么f(x)是{2}關聯.

解題反饋2學生解題情況統計結果顯示，參加解題的十位學生都能完成小問(1)的證明，完成小問(2)證明的學生只有五位.對比問題設計1中的解題情況反饋，通過數學抽象得到“任意的x∈R，都有f(x+1)-f(x)=1”的形式后，學生可以明顯體會到數學抽象的思想和方法，由表征抽象將“f(x1),f(x2)的關系”抽象到“f(x+1),f(x)的關系”.對于小問(2)，有五位學生能夠獨立應用表征抽象將“f(x1),f(x2)的關系”抽象到“f(x+2),f(x)的關系”后得到f(x)是{2}的關聯，這五位學生在這個問題中表現出已經逐步達到了應用數學抽象解決問題的素養要求.完成全部證明過程學生的解題過程歸納如下.

小問(1)解：由f(x)是{1}關聯，則對任意的x1,x2∈R，當x1-x2=1時，都有f(x1)-f(x2)=1.由x1-x2=1，得x1=x2+1，代入f(x1)-f(x2)=1得f(x2+1)-f(x2)=1，故f(x2+1)=f(x2)+1，即f(x+1)-f(x)=1.

小問(2)解：由小問(1)得對任意的x∈R,都有f(x+1)-f(x)=1，同理f(x+2)-f(x+1)=1，上述兩式相加得f(x+2)-f(x)=2，即f(x)是{2}關聯.

解題難點分析：小問(2)中，“f(x)是{2}關聯”的充要條件為“對任意的x1,x2∈R，當x1-x2=2時，都有f(x1)-f(x2)=2”，需要繼續通過數學抽象表述為“對任意的x∈R，都有f(x+2)-f(x)=2”，數學抽象是邏輯推理和表述過程的前提.

難點突破策略：通過數學抽象的表征抽象將“f(x)是{2}關聯”抽象為“f(x+2)-f(x)=2”.

問題設計3對于任意的x1,x2∈R，當x1-x2∈S時，恒有f(x1)-f(x2)∈S成立，則稱f(x)是S關聯.

(1)求證：如果f(x)是{1}關聯，那么對任意的x∈R，都有f(x+1)-f(x)=1.

(2)如果任意的x∈R，都有f(x+1)-f(x)=1，求證：f(x+2)-f(x)=2.

(3)求證：如果f(x)是{1}關聯，那么f(x)是N*關聯.

解題反饋3問題設計3中的小問(2)是主要針對在問題設計2中沒能完成解答的五位學生進行的教學對比實驗，其主要變化是將原先的條件“f(x)是{2}關聯”替換為“f(x+2)-f(x)=2”.統計結果顯示這五位學生對小問(2)都給出了正確的證明，還有學生對小問(3)進行了嘗試證明.對小問(3)的解題過程歸納如下.

小問(3)解：由f(x)是{1}關聯，可知對任意的x∈R，都有f(x+1)-f(x)=1，f(x+1)=f(x)+1，所以對n∈N*，有f(x+n)=f(x+n-1)+1=f(x+n-2)+2=…=f(x)+n，即f(x+n)-f(x)=n，所以f(x)是N*關聯.

解題難點分析：小問(3)的問題設計是由“f(x)是{1}關聯”的特征類比抽象到“f(x)是{2}關聯”，進而由特殊到一般的思想，繼續通過類比抽象得到問題“f(x)是N*關聯”.由問題中的數字運算拓展到字母運算，其難點在于邏輯關系的導出與描述.

難點突破策略：通過由“f(x)是{1}關聯”推理出“f(x)是{2}關聯”的邏輯關系，不難得出“f(x)是{3}關聯，{4}關聯……”類比這樣的遞推關系，可以聯系到數列中的遞推關系，因此可以通過類比抽象的思想，應用數列中遞推關系的表述方法來證明f(x)是N*關聯.

在函數的性質中，函數的奇偶性、單調性、周期性等性質都可以嘗試通過數學抽象達到理解內化的過程.以函數的奇偶性為例，關于偶函數定義中“對于任意的x∈D，都有f(-x)=f(x)”的理解，通過弱抽象可以表述為“定義域內的任意兩個互為相反數的自變量，它們對應的函數值相等”，通過強抽象可以表述為“對于任意的x1,x2∈D，當x1+x2=0時，都有f(x1)=f(x2)”，這種抽象到x1,x2來定義的形式，可以與函數單調性的定義形式統一起來.用相同的x1,x2來定義不同的函數性質可以幫助學生體會這些性質的共性以及本質特征，啟發學生的抽象思維.函數的性質本質上是由自變量和因變量的變化特征所體現出來，所以在表征抽象之后可以通過弱抽象幫助學生理解函數的本質，通過強抽象幫助學生用不同方式嚴謹而準確地表述函數性質.學生對于學習內容掌握的關鍵在于能夠將所要研究的數學對象抽象到能夠理解內化的文字語言、符號語言和圖像語言.關于數學抽象、邏輯推理和數學建模，史寧中教授給出這樣的理解：通過抽象，在現實生活中得到數學的概念和運算法則，通過推理得到數學的發展，然后通過模型建立數學與外部世界的聯系.可以看出，無論是由現實生活到數學概念的抽象，還是在數學問題解決過程中的數學抽象思維，都體現了數學抽象作為數學素養的核心價值.