扁平微槽道熱管蒸發冷凝極限模型

周 豪，孫志堅，龐逸晨，俞自濤，2

（1.浙江大學 能源工程學院 熱工與動力系統研究所，浙江 杭州 310027；2.浙江大學 能源清潔利用國家重點實驗室，浙江 杭州 310027）

0 引 言

強化傳熱同時減小熱管理系統的尺寸和體積一直是學者們深入研究的內容[1]。 目前已經開發了很多新型微冷卻技術，其中，微熱管技術自從1984 年被Cotter[2]首次提出后，是目前行之有效的方法之一。 熱管利用工質的蒸發和冷凝進行傳熱，由于一般情況下相變潛熱遠大于顯熱，因此不需要在熱源和冷源之間存在較大的溫差，即可使熱管具有較好的傳熱性能[3]。 此外，在一定飽和壓力下相變發生時飽和溫度是恒定的，因此熱管還具有較好的均溫性能[4]；同時，熱管借助相變的原理省去了單相冷卻技術所需的高泵浦功率要求[5]，不需額外的外部能耗。

在目前已經開發的多種新型微冷卻技術中，扁平微槽道熱管由于其優異的傳熱性能、良好的均溫性、簡便的加工方法等優勢在電子器件冷卻[6，7]等領域得到廣泛的應用。 但熱管的傳熱性能容易受到各種運行參數[8]和結構參數[9-11]的影響。 不同的應用場景對應著不同的運行參數，有不同的散熱需求，針對特定的運行參數應選取合適的結構參數，如充液率[12]，使熱管發揮最大傳熱能力。 而通過實驗優化熱管結構參數不但成本高，而且十分耗費時間和精力，因此，通過建立理論模型探究熱管的傳熱極限具有十分重要的意義。

目前學者們主要開發了兩類方法計算熱管的傳熱極限。 第一類方法是根據傳熱極限的產生機制，建立經驗關聯式，分別描述冷凝傳熱極限、粘滯極限、冷凍啟動極限、連續流動極限、聲速極限、攜帶極限、毛細極限和沸騰極限[13-16]。 這一類方法簡便直接，容易操作，但是由于熱管的種類和形式過于繁多，關聯式僅能提供基本的定性預測功能，并不能針對不同種類的熱管均給出相對準確的傳熱極限預測結果。

針對扁平微槽道熱管的多項研究表明，毛細極限是其主要傳熱極限[17，18]，因此，學者們建立了基于熱管流動模型的毛細極限計算模型[17，19]。 該方法主要基于質量守恒、動量守恒Young-Laplace方程，具有較高的精度且能從本質上描述熱管發生傳熱極限的機理，因而具有較大的工程應用和理論指導價值。 但在這類方法中，學者們普遍僅考慮了由于蒸發段蒸干導致的毛細極限，而沒有考慮隨著充液率或加熱功率的增加，冷凝段出現液堵所導致的毛細極限[20]，這是需要改進的地方。

本文提出了一種基于一維流動模型的鋁—丙酮扁平微槽道熱管毛細極限模型，同時考慮了由于蒸發段蒸干導致的蒸發極限和由于冷凝段液堵導致的冷凝極限，在液堵段考慮了接觸角的變化。針對一維流動模型、蒸發極限模型和冷凝極限模型三部分分別給出求解算法，并以此探究充液率對熱管性能的影響。 文中給出了流場參數、蒸發極限和冷凝極限隨充液率變化的計算結果并進行相應討論。

1 模型建立

1.1 一維流動模型建立

本文所研究的扁平微槽道熱管單一槽道如圖1（a）所示，槽道形狀為梯形，槽道截面尺寸如圖1（b）所示。 扁平微槽道熱管的蒸發和冷凝極限模型是建立在流動模型的基礎上，由于槽道的軸向尺寸比截面尺寸要大的多，同時考慮到熱管的對稱性，僅需要對一條槽道建立一維模型[21]。提出如下假設：（1）汽液兩相均不可壓縮；（2）工質的熱物性不沿熱管軸向變化；（3）流動為層流；（4）彎液面的軸向曲率半徑為無窮大；（5）熱管水平放置，忽略重力影響。

圖1 槽道形狀與截面尺寸

質量守恒關系如圖2（a）所示，質量守恒方程為：

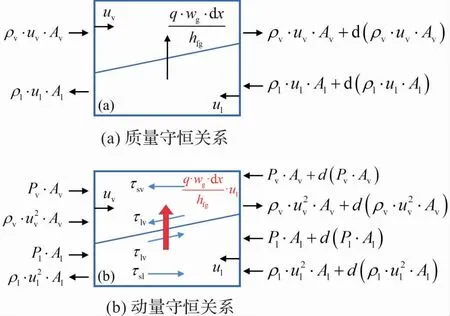
圖2 質量與動量守恒關系

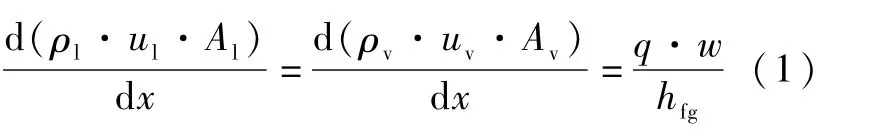
式中，下標l和v分別表示液相和氣相，ρ為密度，u為速度，A為截面積，w為單個槽道的寬度，hfg為汽化潛熱，x為軸向坐標，q為熱流密度，由式（2）計算。

式中，下標e和c分別表示蒸發段和冷凝段，l為長度，Qin為蒸發段的加熱功率，本文僅考慮蒸發段均勻加熱的情況，且為了簡便計算，假定冷凝段也為均勻熱流邊界條件，同時本文研究熱管的穩態，假定冷凝段總換熱功率等于蒸發段的加熱功率Qin。

以蒸發段為例的動量守恒關系如圖2（b）所示，絕熱段和冷凝段同理，其中，控制體內由于相變導致的動量變化被考慮在內，液相和氣相的動量守恒方程分別為

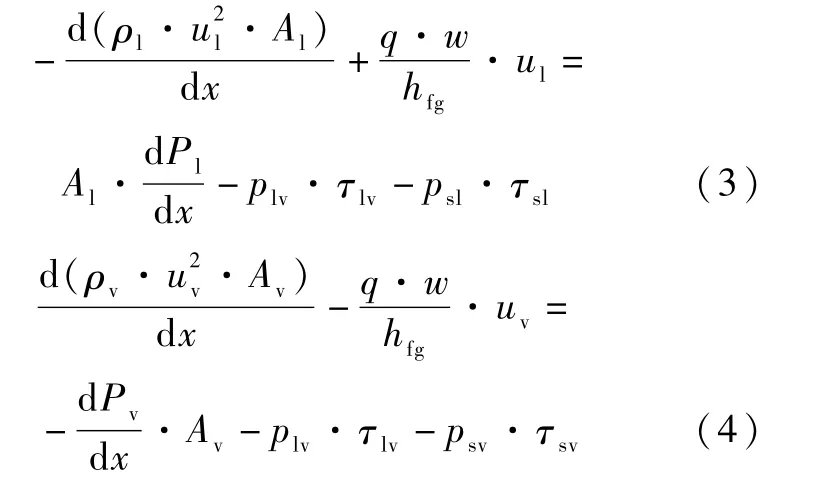
式中，下標s表示固相，P為壓力，p為界面長度，τ為剪切應力。

在扁平微槽道熱管中，有表面張力產生的毛細壓力是驅動冷凝段液化工質回流的主要驅動力，毛細現象由Laplace-Young方程描述，如式（5）所示。

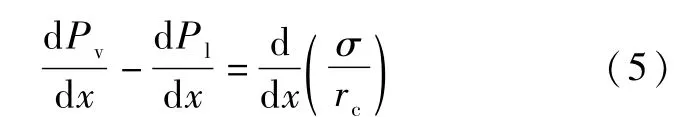
式中，σ為表面張力，rc為截面上彎月面半徑。

由于已經假定流動為層流，所以對氣液兩相均有

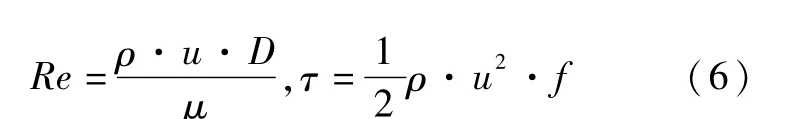
式中，Re為雷諾數，D為槽道當量直徑計算方法如式（7）所示，μ為工質動力粘度，f為摩擦系數。摩擦系數f和雷諾數Re的乘積為泊肅葉數Po，泊肅葉數Po是僅取決于幾何結構的無量綱數，在本文中，液相和氣相的泊肅葉數Po分別取值14.2 和24[17]。 此外，由于氣相速度和液相速度相差很大，氣液界面處的剪切應力計算可以假設液相靜止。

式中，θ為彎月面對應圓心角，δ為液膜厚度，其余幾何參數于圖1（b）中標出。

1.2 蒸發極限模型建立

蒸發極限模型已經被學者們廣泛研究，本文僅做簡要介紹。 隨著加熱功率的提高，蒸發段的工質不斷蒸發并流向冷凝段，如果槽道表面提供的毛細力不足以將冷凝段液化的工質及時輸運回蒸發段，就會產生蒸發段蒸干的現象，此時，熱管的總熱阻會迅速增加，蒸發段表面的溫度會急速上升，達到蒸發極限。 判定熱管達到毛細極限的標準為蒸發段初始處彎月面半徑達到最小值，如式（14）所示，此時彎月面底部接觸槽道底部。 此類情況在熱管充液率較低時更容易發生，具體求解算法請參見本文2.2 節。

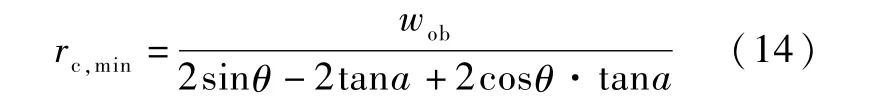
式中，a 為槽道傾斜角。

1.3 冷凝極限模型建立

除蒸發段蒸干可能導致扁平微槽道熱管達到毛細極限之外，對于充液率較大的熱管，冷凝段的液堵也是使熱管達到毛細極限的條件之一，而這一問題往往被學者們忽略。

液堵段液膜分布如圖3 所示。 在未出現液堵時，冷凝段末端的液膜位于1 位置，彎月面上沿尚未接觸到槽道的頂角處。 隨著加熱功率的提升，冷凝段末端的液膜位置逐漸上移，首先達到2 位置，此時彎月面上沿剛好接觸槽道的頂角處。 此前的多項研究均認為此時熱管達到了毛細極限，其實并非如此。 由于表面張力的存在，隨著加熱功率繼續增加，液膜后續并不會溢出槽道，而是會有一個液膜逐漸變平、接觸角逐漸變大的過程，液膜形狀會從形狀2 逐漸向形狀5 過渡，而液膜形狀為2 的位置會從冷凝段末端向蒸發段的方向逐漸移動。 在本文中約定，液膜形狀為2 的位置到冷凝段末端之間的部分為液堵段。

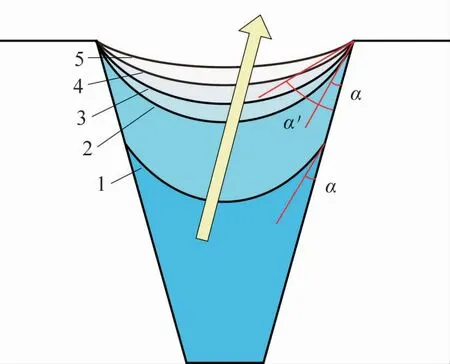
圖3 液堵段液膜變化示意圖

在液堵段，工質的接觸角會沿熱管軸向發生變化，接觸角和彎月面半徑之間的關系如式（15）所示。 在求解過程中，只需要把式（8） ～式（13）中的θ用θx進行替換，就可以照常計算，不會增加新的變量。

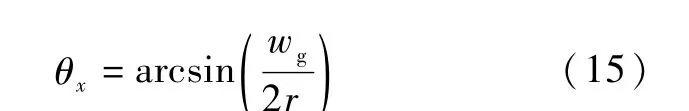
根據液堵段的定義，冷凝段末端的彎月面半徑可以趨于無窮大，且液堵段的長度可以等于熱管的總長度，這明顯是不合理的，因此，本文假定，當液堵段的長度等于冷凝段的長度時，熱管達到冷凝極限，此時冷凝段初始位置的彎月面頂部恰好上升至槽道頂部，此處彎月面半徑值如式（16）所示。

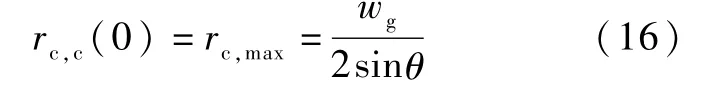
2 模型求解算法

2.1 一維流動模型求解

在一維流動模型中，式（1）、式（3） ～式（5）共同構成了二階常微分方程組，共五個方程，含有ul、uv、Pl、Pv、rc五個變量，可以使用四階龍格庫塔方法進行求解，只需要指定迭代初值和迭代步長。 在本文中，迭代初值如式所示，迭代步長選取為0.001 m。

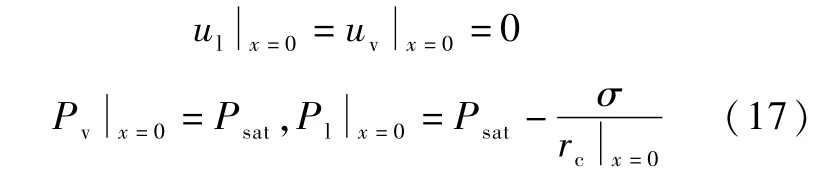
式中，Psat表示工作溫度所對應的飽和壓力，工作溫度為事先設定值，此外，彎月面半徑rc的初值選取與求解的過程有關，具體請參見本文2.2 節和2.3 節。

本文所研究熱管工質為丙酮，管殼材質為鋁，工質的物性參數根據工作溫度值進行差值選取，物性數據庫選用Nist數據庫，差值方法為MATLAB R2019b 保型三段插值法。 本文所研究扁平微槽道熱管的幾何參數如表1 所示。 本文所有程序通過MATLAB R2019b 實現。

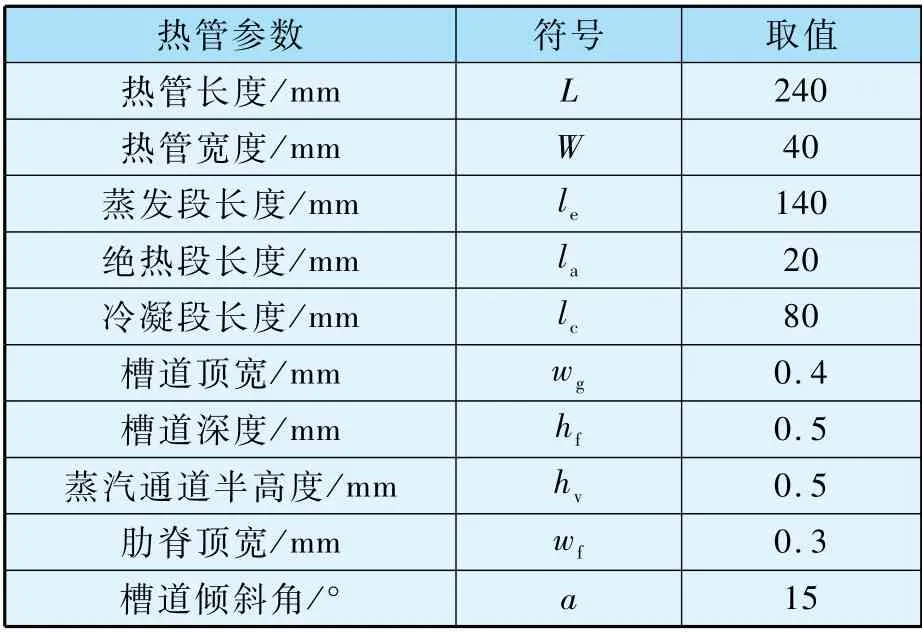
表1 扁平微槽道熱管幾何結構參數

2.2 蒸發極限模型求解

本小節提出了求解給定扁平微槽道熱管蒸發極限計算的方法。 對于給定的扁平微槽道熱管，充液率是確定，而充液率并不在模型的輸入參數中，只能通過模型輸出的液膜分布來核算，因此需要使用迭代求解的方法去逼近所給定的充液率值。

首先需要求解流動模型，迭代初值由式（14）和式（17）確定，然后假設加熱功率，求解流動模型得到液膜分布進而得到充液率的計算值，充液率被定義為熱管內的工質在液相時的體積占槽道體積之比，其計算方法如式（18）所示。 通過不斷迭代調整加熱功率的值，當計算充液率與設定充液率之差小于給定誤差時，認為模型收斂，熱管達到蒸發極限。 其中，由于熱管被分為蒸發段、絕熱段和冷凝段三部分，每一部分控制方程并不相同，因此每一部分末端的計算結果為下一部分的計算初值。 算法流程圖如圖4 所示。

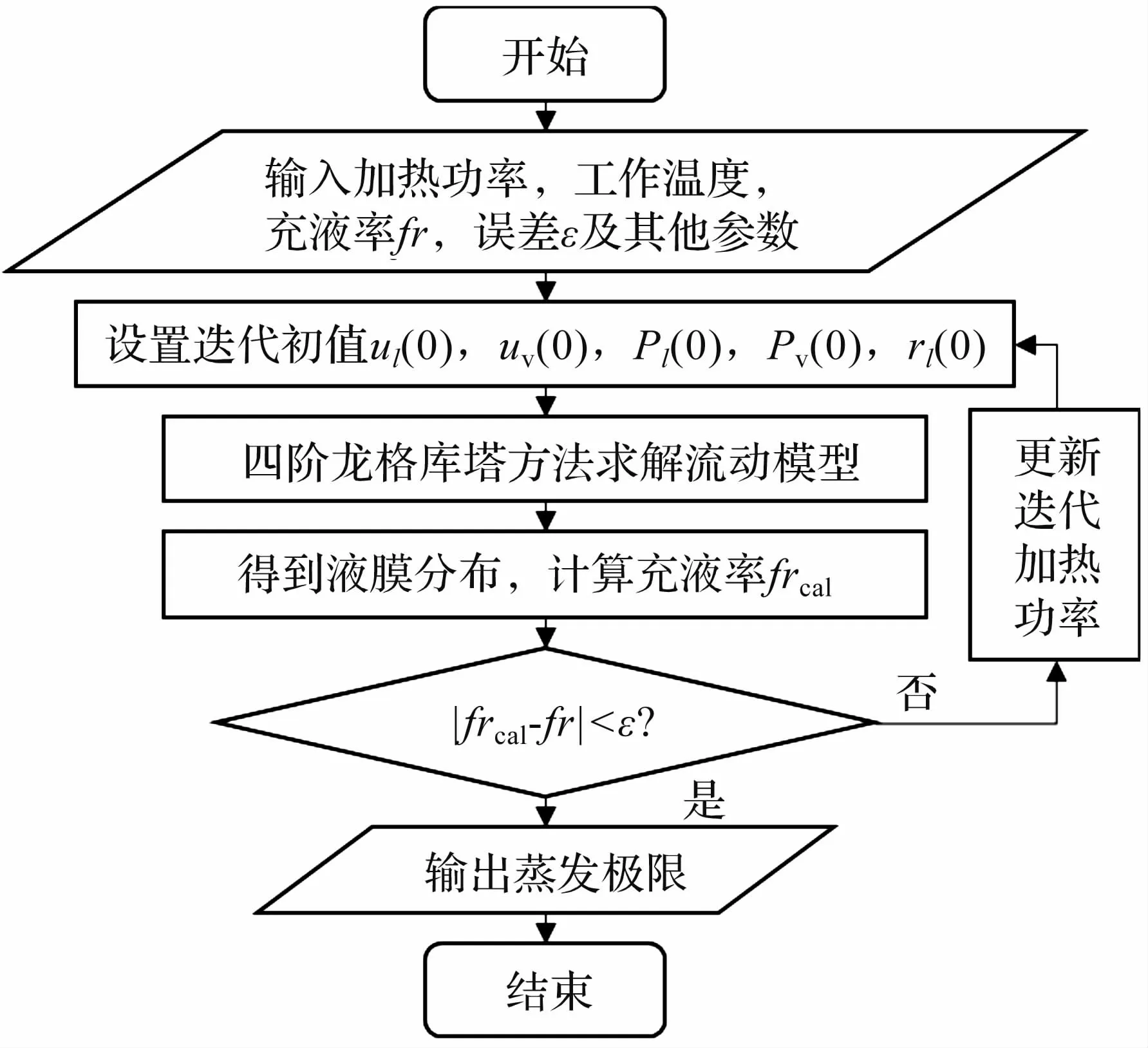
圖4 蒸發極限計算流程圖

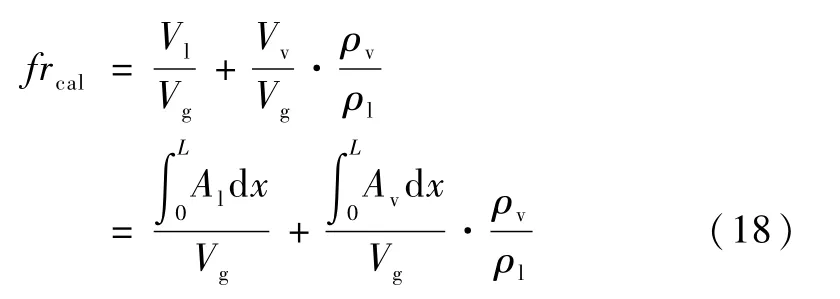
2.3 冷凝極限模型求解

本小節給出求解扁平微槽道熱管冷凝極限的計算方法。 與蒸發極限的計算不同，冷凝極限需要求解含液堵段的方程組，由于本文認為液堵段長度等于冷凝段時，熱管達到冷凝極限，因此，熱管被分為蒸發段、絕熱段和液堵段三部分。

我們無法確定在事先假定的加熱功率下，熱管是否會發生液堵，且液堵段長度等于冷凝段長度，因此，需要先求解不含液堵段的方程，確定液堵段長度，通過迭代加熱功率使液堵段長度等于冷凝段長度，再求解含液堵段的方程組求得此冷凝極限所對應的液膜分布和充液率。

此外，冷凝極限是由于充液率過多導致冷凝段出現液堵，此時蒸發段不一定出現蒸干現象，因此蒸發段初始位置彎月面半徑是未知的，不可能像求解蒸發極限時通過迭代調整加熱功率來匹配充液率那樣進行計算。

為克服上述困難，本文提出了一種遍歷對比的方法求解冷凝極限，即針對一系列的彎月面半徑迭代初值進行求解，得到一系列充液率和加熱功率的對應組，然后針對相同充液率所得的所有加熱功率取最小值作為其冷凝極限。 具體算法流程圖如圖5 所示。 需要指出的是，最后一步的判斷計算充液率是否小于0.8 并無特殊意義，只是當充液率過大時，毛細極限較小，失去了計算的意義，因此選擇較大的充液率值0.8 作為計算停止的條件。

3 結果與討論

3.1 一維流動模型求解結果與討論

圖6 -圖10 給出了一維流動模型在加熱功率為5 W，充液率為20%、23%和26%時的計算結果，分別展示了鋁—丙酮扁平微槽道熱管液相速度、氣相速度、液相壓力、氣相壓力和彎月面半徑沿熱管軸向的變化。

從圖6 可以看出，液相速度的最大值隨著充液率的提升逐漸降低，這是由于充液率的增加導致液相體積增加，固液界面增加，使得剪切應力增加，從而使液相所能增加到的最大速度減小。 從圖8 可以看出，隨著充液率的增加，相同位置的液相壓力逐漸增加，且沿軸向的總液相壓力損失逐漸減小。 這是由于隨著充液率的增加，液面逐漸平緩，使得熱管初末位置的彎月面半徑相差變小，由于氣相壓力基本保持恒定，根據Young-Laplace方程可知，液相壓力沿軸向變化逐漸減小。 相同的趨勢也可以從圖10 中看出。

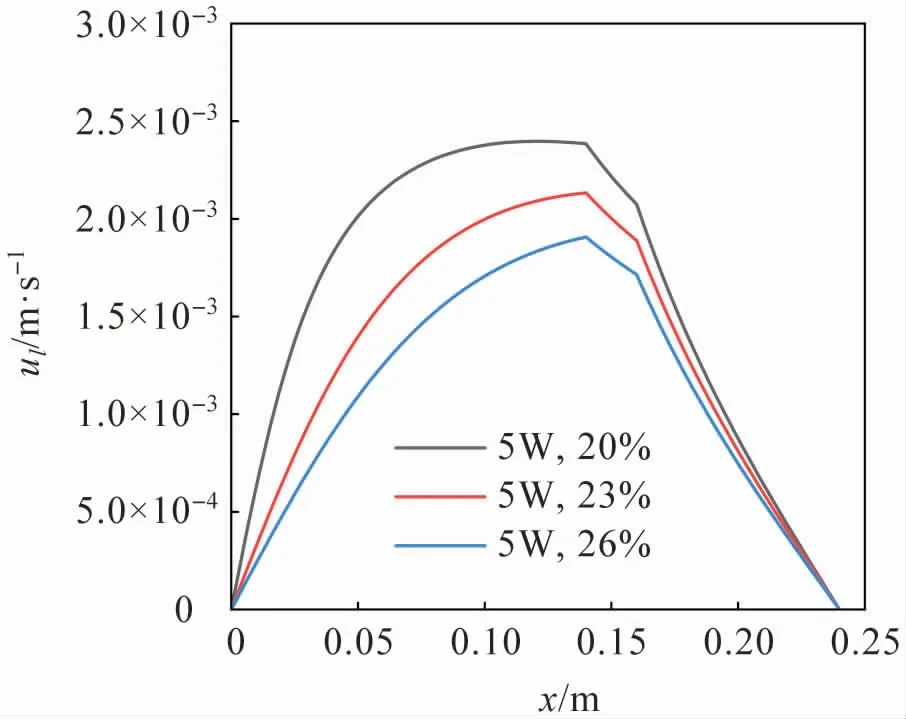
圖6 液相速度沿熱管軸向變化

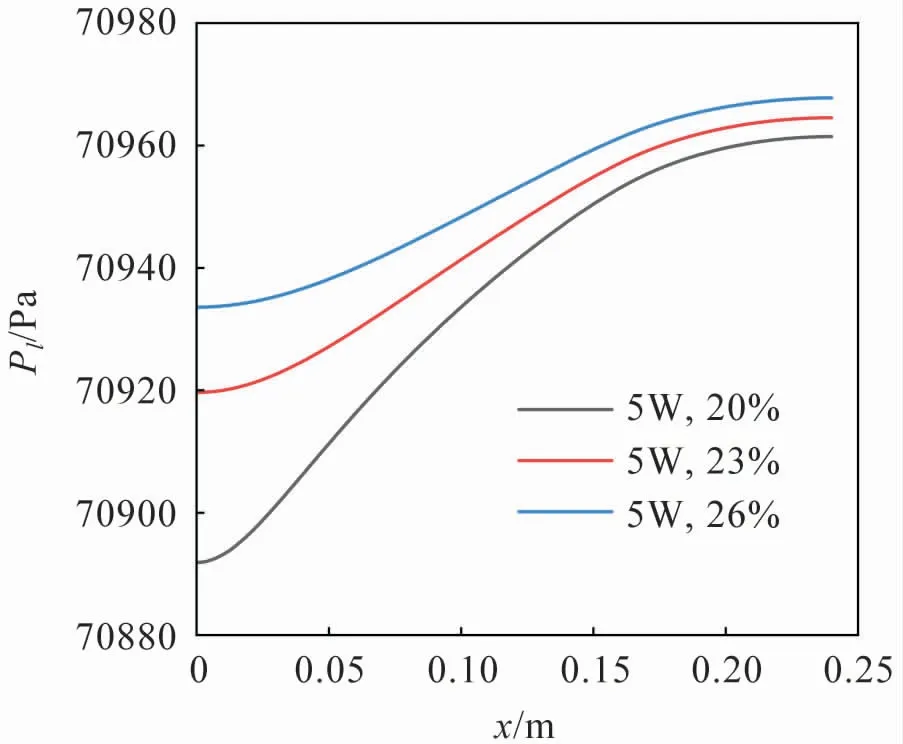
圖8 液相壓力沿熱管軸向變化

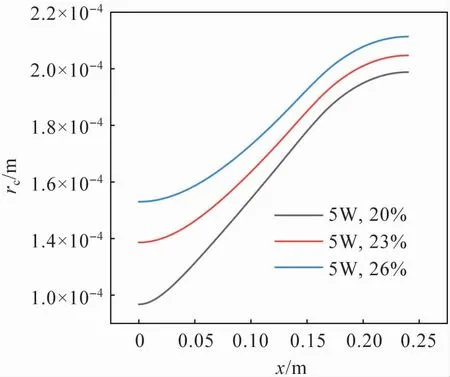
圖10 彎月面半徑沿熱管軸向變化

圖7 和圖9 給出氣相速度和壓力隨熱管軸向距離的變化，可以看出，在同一加熱功率下，氣相參數隨充液率的變化較小，這是因為在相同的加熱功率下，熱管的工作溫度是基本相同的，這使得氣相工質在相近的飽和溫度下具有相近的飽和壓力，進而具有相近的物性參數，得到相近的速度分布。

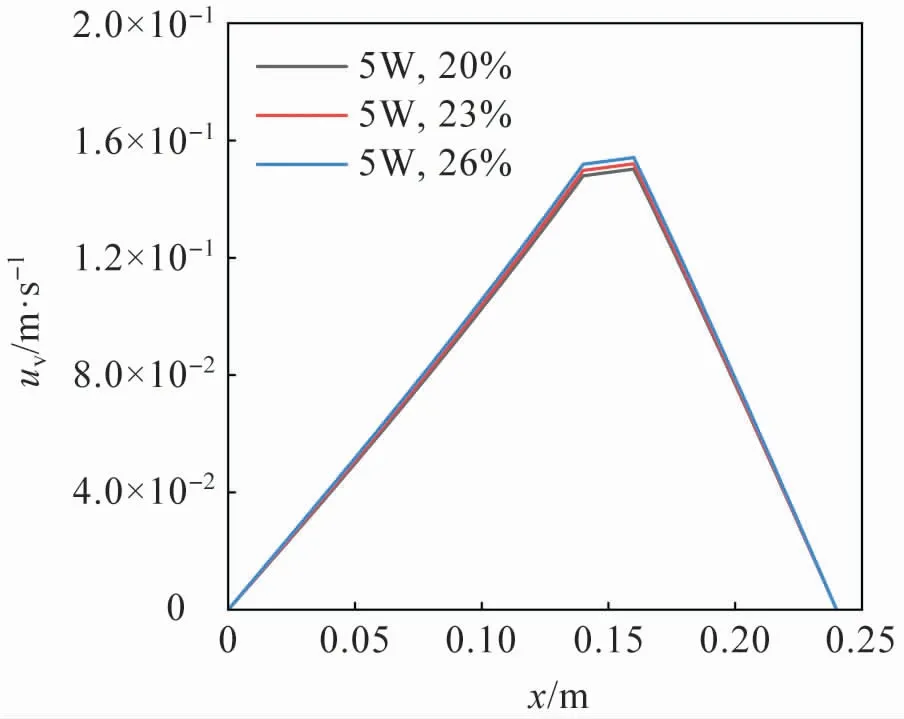
圖7 氣相速度沿熱管軸向變化

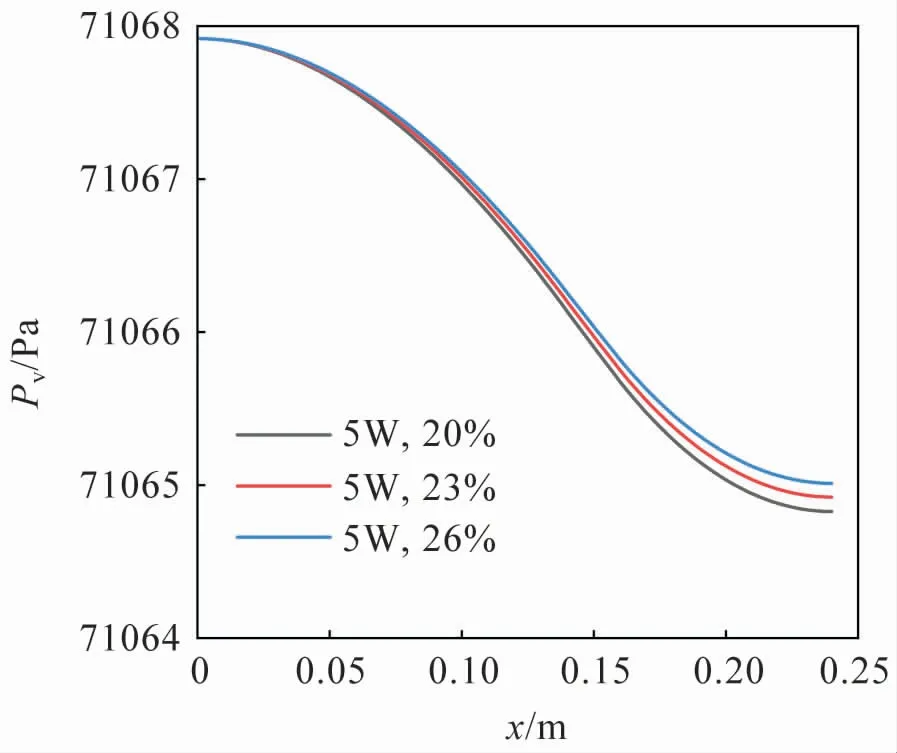
圖9 氣相壓力沿熱管軸向變化

3.2 蒸發極限模型求解結果與討論

圖11 給出了所研究扁平微槽道熱管蒸發極限隨充液率的變化情況，可以看出，隨著充液率的增加，蒸發極限逐漸增加，這是由于熱管的蒸發段中含有更多的工質進行蒸發，可以帶走更多的熱量，避免蒸干現象的出現，進而提高熱管的蒸發極限。

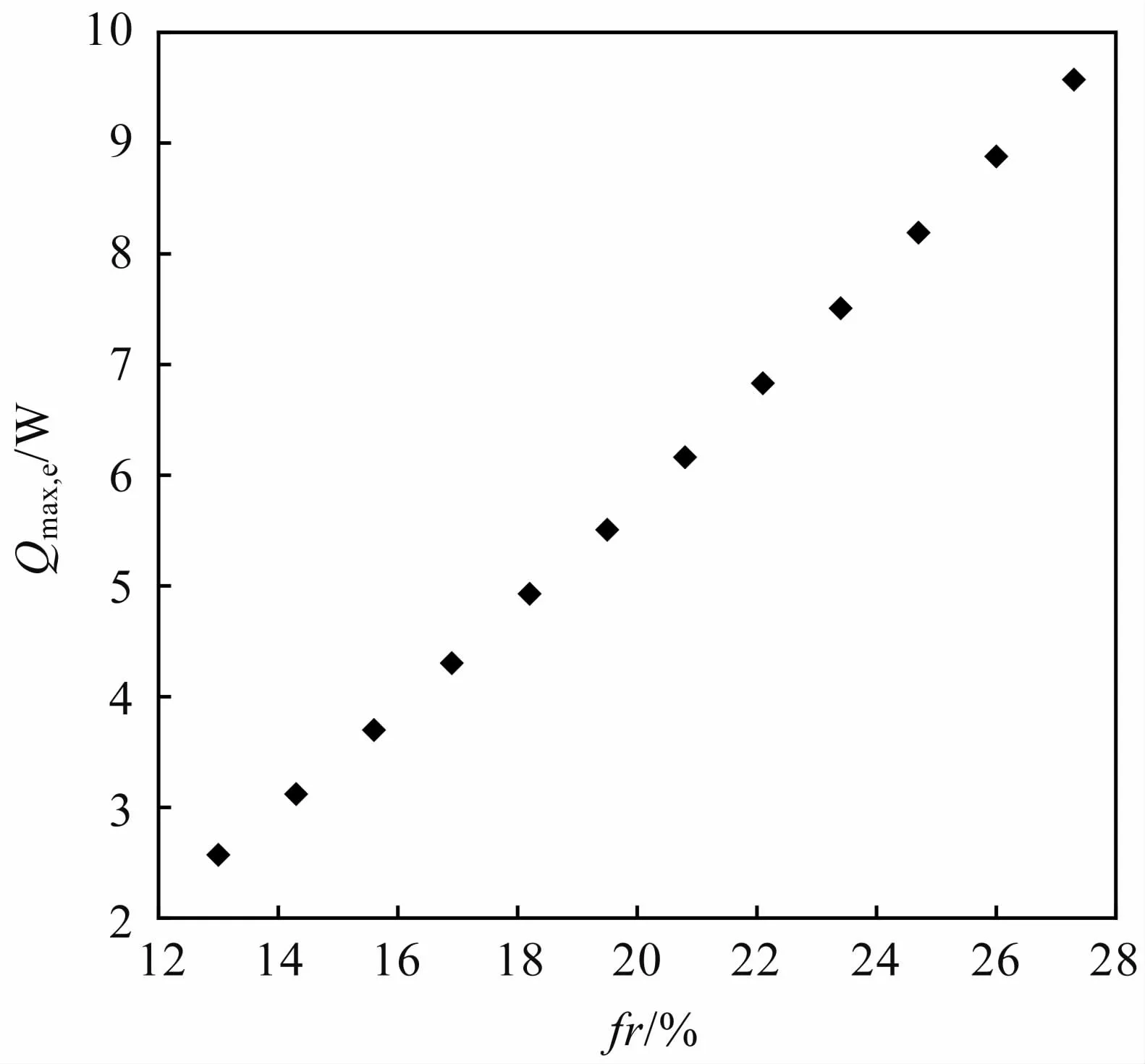
圖11 蒸發極限隨充液率變化

3.3 冷凝極限模型求解結果與討論

圖12 給出了所研究扁平微槽道熱管冷凝極限隨充液率的變化情況，可以看出，隨著充液率的增加，冷凝極限逐漸降低，這是由于隨著充液率的增加，冷凝段積累了更多的液相工質，液膜的增厚導致其導熱熱阻增加，進而使得熱管整體熱阻增加，傳熱性能下降。

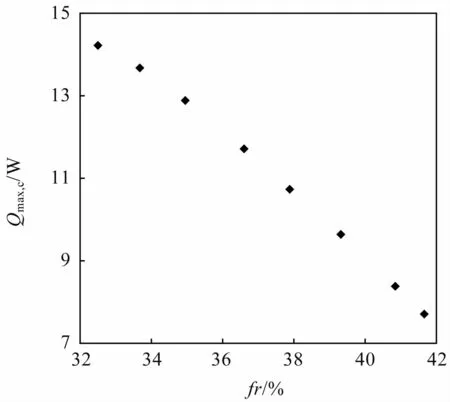
圖12 冷凝極限隨充液率變化

對比圖11 和圖12 可以發現，蒸發極限和冷凝極限的最大值之間有4W 左右的差距，且充液率之間也有8%左右的差別，這是因為該模型沒有考慮冷凝段出現部分液堵段時的蒸發極限。 該極限的獲得需要通過事先求解不含液堵段的方程確定液堵段長度，然后求解包含液堵段在內的四段方程組來獲得，這將是今后的工作內容。 目前的模型可以說明，在現行結構下，扁平微槽道熱管的最佳充液率在27% ～32%之間。

對于任意類似結構的扁平微槽道熱管，均可以使用該模型對其充液率進行優化，得到熱管最佳充液率，或者其對應的毛細極限，這對于特定工況下選擇適當熱管具有重要指導意義。

4 結 論

本文提出了一種基于一維流動模型的鋁—丙酮扁平微槽道熱管毛細極限模型，同時考慮了由于蒸發段蒸干導致的蒸發極限和由于冷凝段液堵導致的冷凝極限，在液堵段考慮了接觸角的變化，并以此探究充液率對熱管性能的影響。 計算結果表明：

（1）在相同加熱功率下，隨著充液率的增加，液相流動損失增加，液相回流最大速度減小，彎月面趨于平緩，充液率對氣相參數影響較小；

（2）隨著充液率的增加，蒸發極限逐漸增加；

（3）隨著充液率繼續增加，蒸發極限不會達到，冷凝開始下降；

（4）所探究熱管毛細極限在14 W 左右，相應的最佳充液率在27% ～32%之間。