基于格子Boltzmann方法的曲面接觸熱阻模擬

繆紅林，張 良

（浙江大學 熱工與動力系統研究所，浙江 杭州 310027）

0 引 言

接觸熱阻作為制約傳熱過程的關鍵熱阻之一，在航天[1]、微電子[2-3]、超導[4]、能源[5]等領域的熱設計和熱管理中具有重要影響。 準確預測和分析導熱材料間的接觸熱阻形成機理和規律，并實現對接觸熱阻特征的主動控制，對于傳熱器件散熱結構的優化設計，提升傳熱性能和能效水平具有重要的意義。

現有研究表明，材料的性質，接觸面的形貌特征，間隙介質、接觸面載荷及環境等是影響接觸熱阻的主要因素[6]。 目前大量有關接觸熱阻的理論研究[7-8]和實驗研究[9-12]工作得以開展，其中，實驗研究主要圍繞具體材料在不同溫度、壓力條件下的接觸熱阻特征進行測量。 實驗測量法大致可以分為適用于測量較厚材料的穩態測量法[9]和適合測量薄膜材料的瞬態測量法[10]。 如馮飆等[11-12]提出的改進版穩態測量法，可用于測量亞毫米厚度材料間的接觸熱阻，并將測量誤差控制在5%以內。

相較于實驗研究，部分研究者致力于采用數值方法對不同因素的影響規律進行更為系統和深入的分析，以期望實現接觸熱阻的準確預測：Xiang等[13]采用非平衡的分子動力學方法模擬接觸熱阻，Gou 等[14]將材料真實物理形貌導入ANSYS 軟件，使用有限元方法求解接觸熱阻。 其中，在數值模擬方法中，由于介觀尺度的格子Boltzmann 方法在處理具有復雜邊界的傳熱模型上具有一定的優勢[15]，因此采用該方法對接觸截面上的具有復雜形貌特征的接觸熱阻的計算更為有效。 在基于格子Boltzmann 方法的研究中，根據模型中熱阻值是否已知，可以將之分為兩類。 一種是在已知接觸熱阻值的情況下，在模型的接觸面處添加接觸熱阻影響的部分反彈法[16-17]和粒子圖像法[18]，這兩種方法都可以在傳熱模型中便捷地添加接觸熱阻的影響。 另一種則是考慮到接觸面形貌，形變模型和傳熱模型的建模方法：崔騰飛等[19]使用多尺度方法研究高斯表面間的接觸熱阻，在接觸面加密網格并使用格子Boltzmann方法求解傳熱問題，非接觸面則使用有限差分法加速計算；方文振等[20]提出的多重網格模擬方法，在接觸面加密網格捕捉平直面上的分形形貌，研究平直面間接觸熱阻的變化規律。 與此同時，當前有關接觸熱阻的研究主要針對的是常見的平面上的接觸熱阻，而對于曲面間的接觸熱阻的研究鮮有報道，而曲面熱阻在以內嵌管式換熱器[21]為代表的傳熱元件中普遍存在。 準確預測固體曲面間的接觸熱阻，理清曲面熱阻與平面熱阻的共性規律與差異，對于相關傳熱元件的傳熱過程理解與優化具有重要的科學和工程意義。

因此，本文建立基于格子Boltzmann 方法的單松弛數值模型對固-固曲面間的接觸熱阻特征進行數值計算，并研究了溫度、壓力、材料和表面粗糙度四種因素對曲面接觸熱阻特征的影響。

1 數值模型

1.1 物理模型

本文采用格子Boltzmann 方法對兩個緊密接觸的等壁厚圓環在恒溫邊界下（Tin，Tout）的傳熱過程模擬計算來研究固—固曲面間的接觸熱阻特性。 其中，外圓半徑rout為2000 μm，內圓半徑rin為1500 μm，兩個圓環不相互接觸壁面設為絕對光滑。 該問題的計算域可以簡化為如圖1 所示的四分之一緊密接觸的扇形，扇形內外壁面為恒溫，兩端為絕熱。

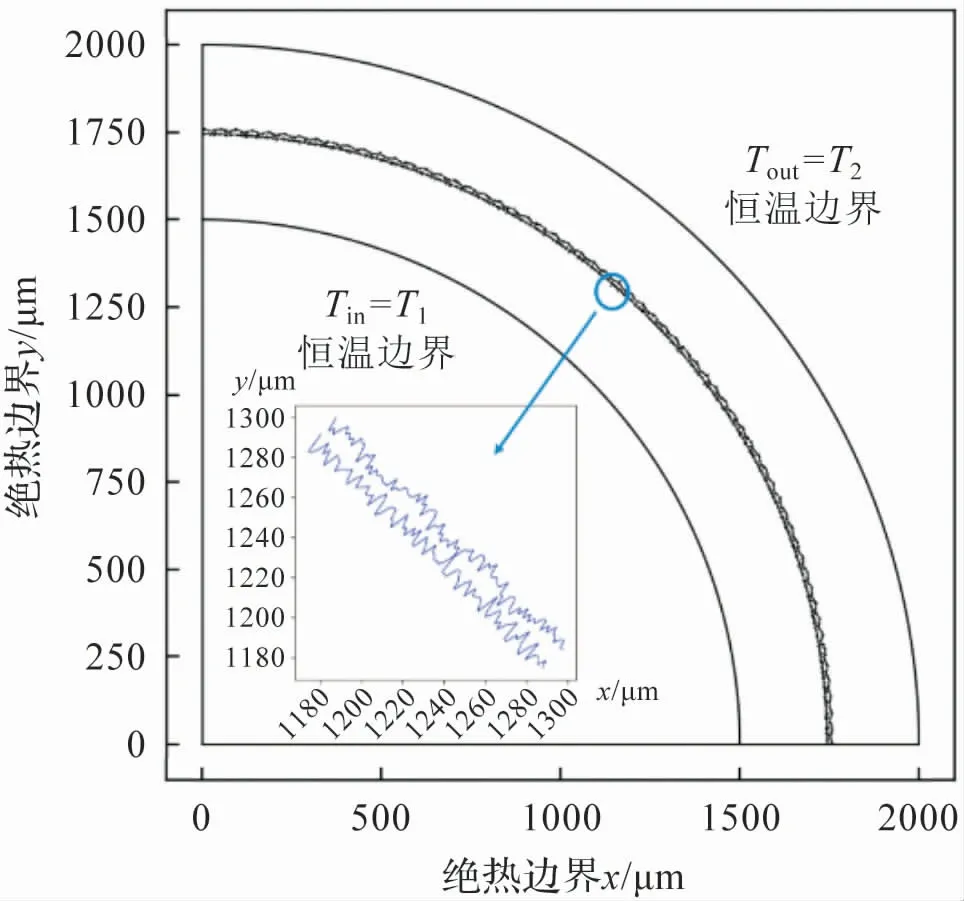
圖1 接觸熱阻模型示意圖

兩個圓環相接觸的圓弧表面形貌特征采用基于分形理論的W-M函數[22]進行描述，使用曲面上均勻遞增的弧長作為W-M函數的參數：

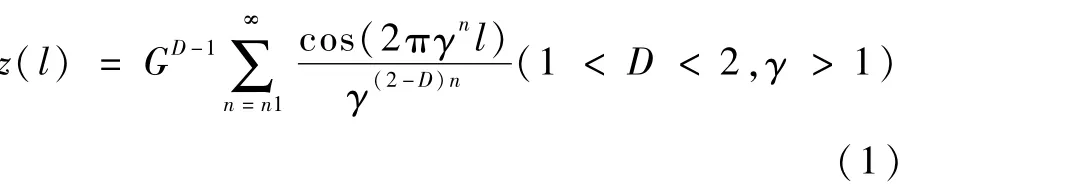
式中：z為分形形貌在曲面法線方向偏離曲面的高度；l為曲面均勻遞增的弧長；G為影響特征曲面高度的分形特征尺度系數；D為影響表面復雜度的分形維數；γ為常數（對于正態分布的隨機輪廓，一般取γ=1.5）；n 為自然序列。本文中選取D=1.4，G=1.0 ×10-9，n =20 ～40 生成表面形貌[23]。

接觸面的粗糙度使用算術平均高度Ra表征：

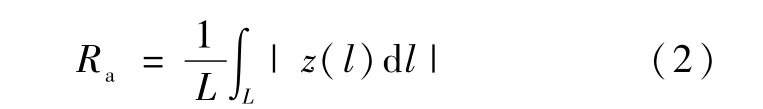
式中：L 為積分總弧長；l為積分微元；z為表面高度。

為了進一步考慮接觸面上的形變特征，在接觸點的形變模型上，使用CMYTCR接觸模型[24]進行描述。 該模型假設接觸形變是純塑性形變，接觸點的受力平衡方程為：

式中：Ar為實際接觸面積；Aa為名義接觸總面積；Hc為材料的微觀硬度。 在模型中由于實際接觸面積占總面積之比很少，因此不考慮塑性形變部分的體積變化。 故壓力的計算方法：

1.2 格子Boltzmann 方法求解

根據上述物理模型及邊界條件特征，其接觸熱阻Rtcr的表達式為：

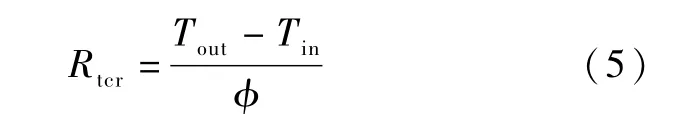
式中：?為曲面上的熱通量（采用二維模管，熱通量單位為W/m）。 為了求得熱通量，需要建立格子Boltzmann 方法對如下二維熱擴散方程進行求解：

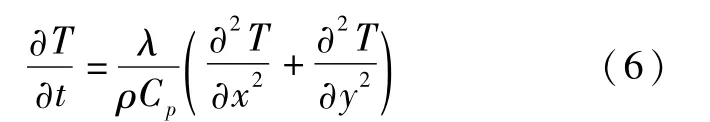
式中：T為溫度；t為時間；λ為材料的導熱系數；ρCp為體積比熱。

本文采用單松弛的格子Boltzmann 方法求解溫度擴散問題的演化方程[25]如下：

如圖2 所示，速度離散使用D2Q5[26]的離散方法。 離散后的速度矢量c為：

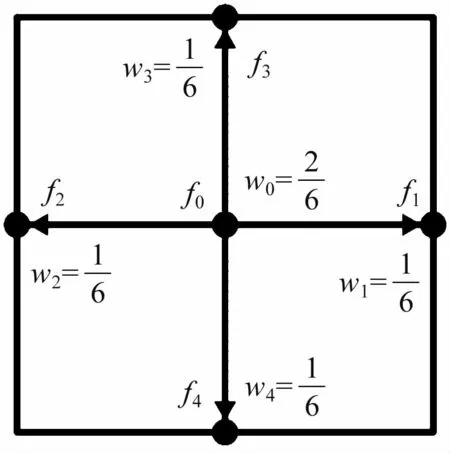
圖2 D2Q5 模型

式中：q1與q2為沿分布函數遷移方向的已知熱流密度，γ和β 分別為兩已知熱流密度與法向熱流密度之間的夾角。

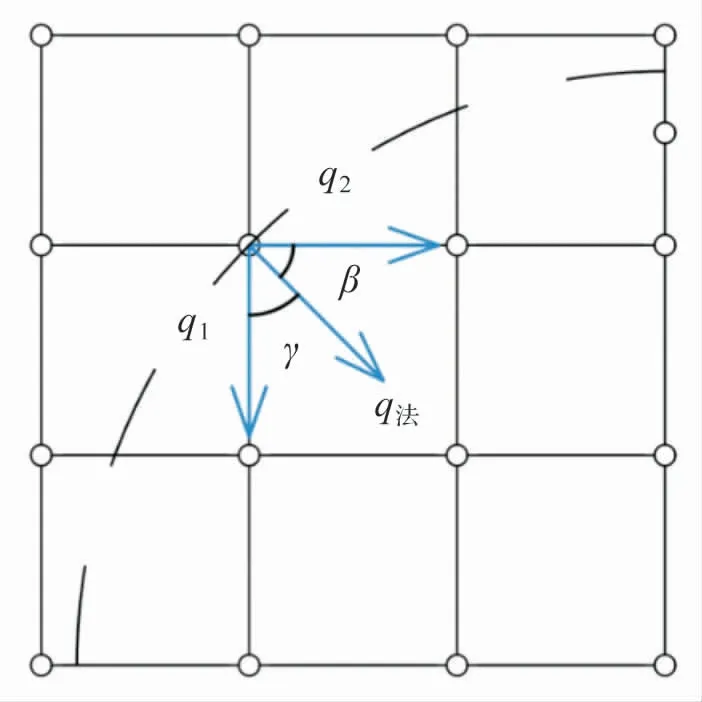
圖3 熱流密度示意圖

在接觸面間的傳熱過程中，以分形曲線為邊界，將空間中的點劃分為固體材料的點與間隙介質的點，熱流需要經過固體材料，流經間隙介質到另一邊的固體材料。 為保證溫度與熱流密度在耦合界面連續，需假設間隙介質與固體材料的體積比熱相等[27]，即：

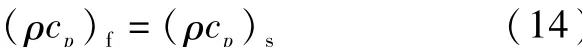
其中，（ρCp）f為間隙介質的體積比熱，（ρCp）s為固體材料的體積比熱。 上述假設，并不影響最終穩態的溫度場。

1.3 曲面邊界的處理

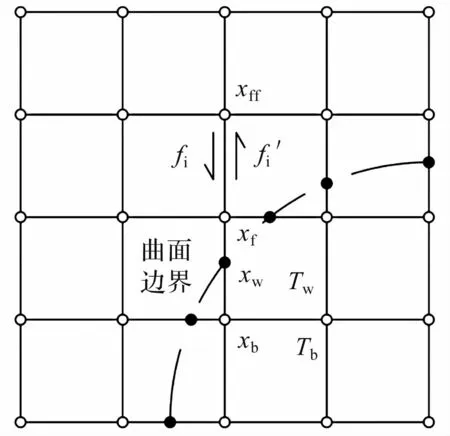
圖4 曲邊邊界示意圖

2 模型驗證

為了驗證本文建立的格子Boltzmann 模型計算曲面上接觸熱阻的可靠性，本文通過對圖1 中的表面粗糙度進行理想光滑處理后進行模擬計算。 其中接觸間隙取20 μm，外壁面與內壁面溫度分別取303 K和293 K。 材料和間隙介質的導熱系數分別取210 W/（m·K）和10 W/（m·K）。其中，熱阻理論解可由以下公式直接求得：

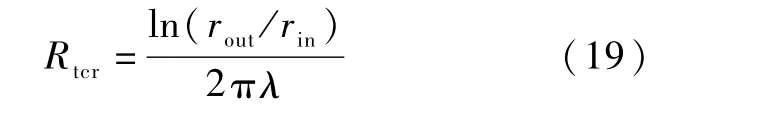
不同網格分辨率的計算結果與理論解之間的誤差如表1 所示。 而且，隨著網格分辨率提高，網格對計算結果的準確性影響遞減。 表明本文建立的格子Boltzmann 模型能夠準確求解曲面邊界的傳熱問題。

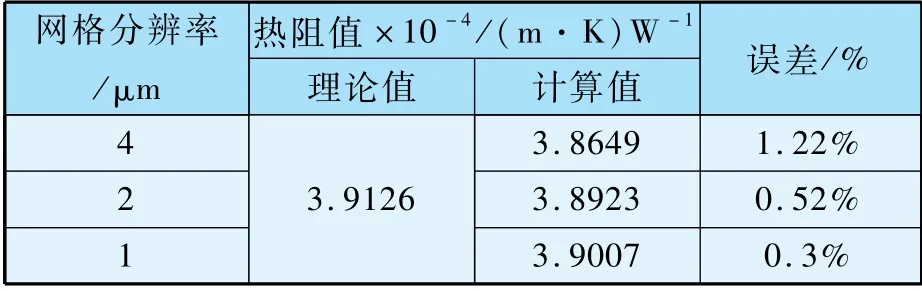
表1 理想光滑間隙下不同網格分辨率的計算模型準確性驗證

與此同時，如表1 所示，隨著網格分辨率的增加，計算誤差越小。 因此，為了進一步驗證實際模型中的網格無關性，本文對圖1 中初始條件下（選取D=1.4，G=1.0 ×10-9，n =20 ～40 生成表面形貌）的粗糙表面下的接觸熱阻計算的網格無關性進行驗證，固體材料為內外壁溫分別為293 K和303 K的不銹鋼圓環，其結果如表2 所示。

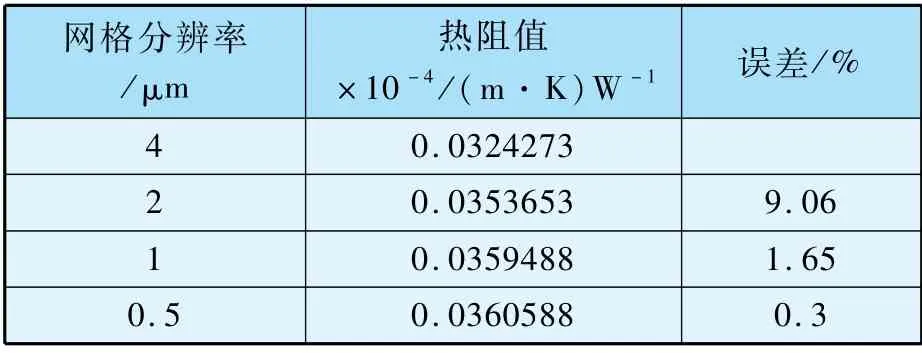
表2 分形形貌下網格分辨率測試

從表2 中可以看出，當網格分辨率從4 μm降低至2 μm時，接觸熱阻提高了9.06%。 而當分辨率從1 μm降低至0.5 μm時，熱阻值僅提高0.3%。 網格對計算結構的影響可以忽略。 考慮計算效率，最優網格分辨率為1 μm。

3 結果與討論

3.1 溫度的影響

如圖5 所示為，內外壁溫分別為293 K和303 K不銹鋼圓環，選取D=1.4，G=1.0 ×10-9，n =20 ～40生成粗糙接觸面，在18.3 MPa壓力下，穩態條件下得到的溫度分布云圖。 通過局部放大可以看出，在接觸間隙附近存在較大的溫度梯度。 這是由于間隙介質空氣的導熱系數遠小于接觸材料，是主要傳熱熱阻，顯著抑制接觸界面間的傳熱。

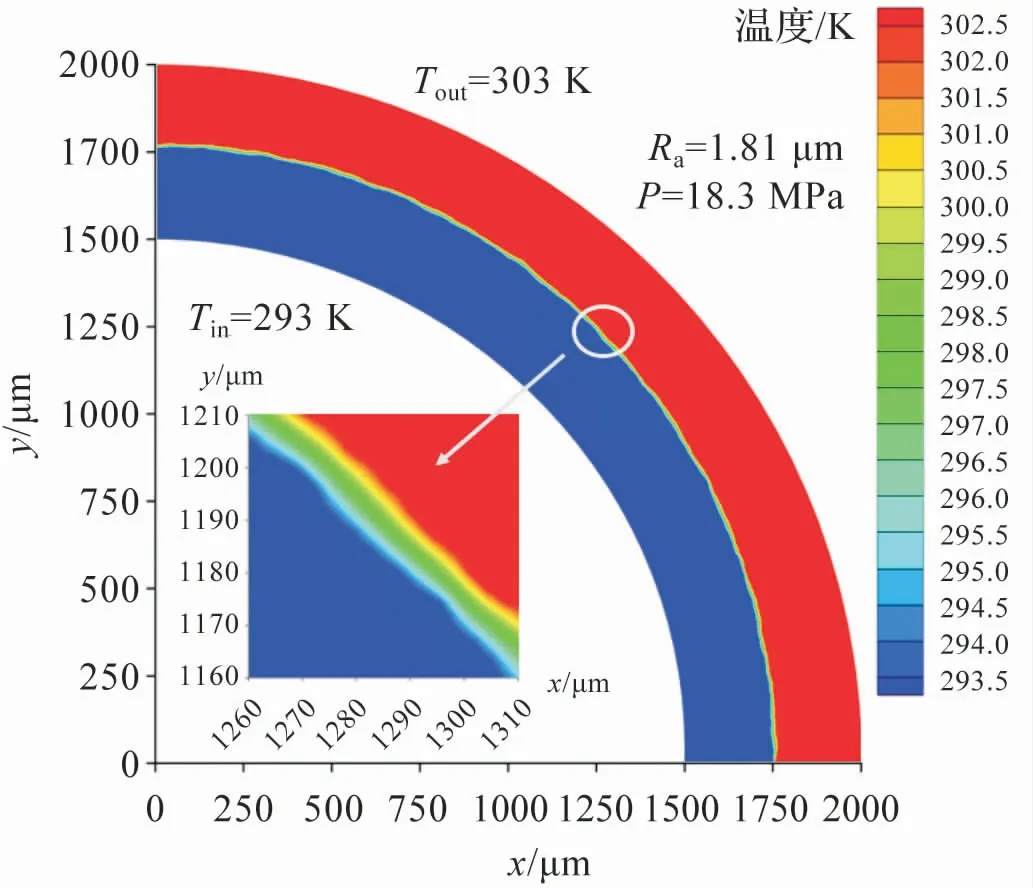
圖5 接觸熱阻的溫度分布云圖

圖6 為不銹鋼接觸熱阻值隨溫度（上下壁面溫度的平均值，其中上下壁面溫差為10 K）的變化規律，接觸熱阻值單調降低，這是因為間隙介質空氣的導熱系數隨著溫度的升高而升高。

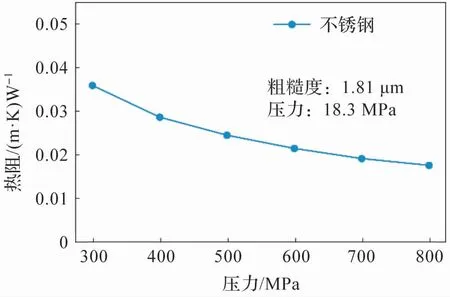
圖6 接觸熱阻隨溫度的變化

上述模擬結果表明，接觸界面區域的傳熱過程主要受間隙介質的導熱系數抑制。

3.2 接觸壓力及接觸材料的影響

如圖7 所示，分別計算了鋁和不銹鋼兩種固體材料環形曲面在特征粗糙度為1.81 μm（選取D=1.4，G=1.0 ×10-9，n =20 ～40 生成表面形貌）的具有分形特征的接觸表面下接觸熱阻隨壓力的變化特征。 從圖中可以看出，兩種材料的接觸熱阻隨壓力的變化規律表現一致，即隨著壓力的增大接觸熱阻呈現出降低的趨勢，且其降低速率逐漸趨于緩和。

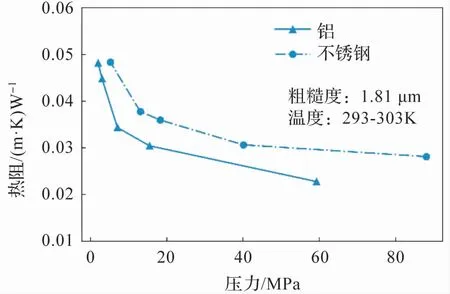
圖7 接觸熱阻隨壓力的變化

為了進一步定量分析壓力對接觸面積影響，本文對不銹鋼材料的接觸面上間隙介質節點數隨壓力的變化特征進行了統計分析，其結果如表3所示。 當壓力從0.8 MPa提高至13 MPa時，間隙介質點平均每兆帕減少898.52 個。 而壓力從40 MPa提高到88 MPa，間隙介質點平均每兆帕減少57.29 個。 對應的，其接觸面的接觸特征如圖8所示，可以看出間隙寬度隨著壓力升高明顯減小。這表明隨著接觸面間的壓力增加，微觀接觸面積會增加，且其增加速率會逐漸變小，壓力對接觸熱阻的影響變得不再明顯。 這一結果與平面下的結論較為一致[21]。 此外，由于不同材料的硬度特征不一樣，導致在同一壓力下其接觸面積不一致，從而導致其接觸熱阻的絕對值上存在差異。 如圖7所示，高硬度的不銹鋼，在同樣壓力工況下，接觸熱阻略大于鋁。

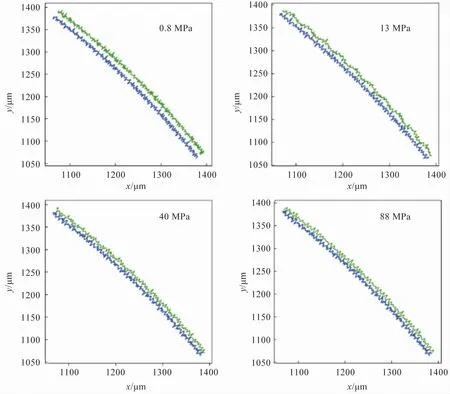
圖8 不同壓力下粗糙表面的接觸情況

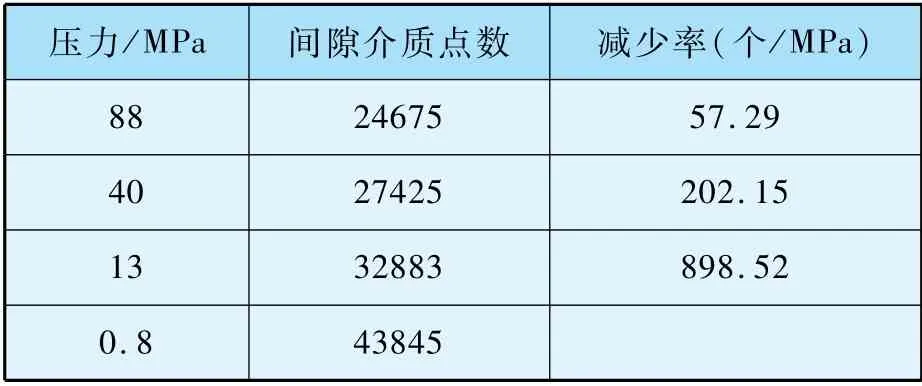
表3 不同壓力下間隙介質厚度量化分析

3.3 表面粗糙度的影響

為研究表面粗糙度對曲面間接觸熱阻的影響規律，本文選取內外壁面溫度為293 K與303 K，間隙介質為空氣，接觸材料為不銹鋼，選取D=1.4，n =20 ～40 生成分形表面形貌，并通過改變分形特征尺度系數G來控制材料表面粗糙度，分別計算幾種粗糙度下不同壓力工況的接觸熱阻，具體模擬參數如表4 所示。

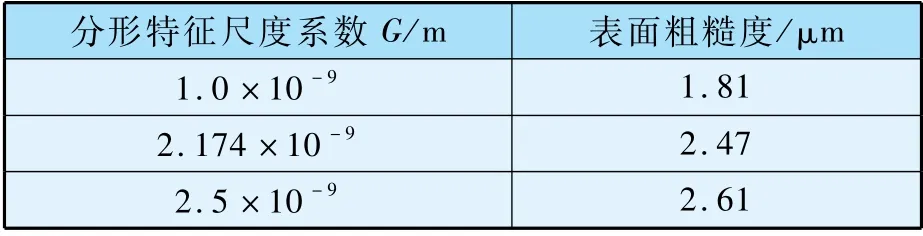
表4 分形特征尺度系數與表面粗糙度

接觸熱阻隨表面粗糙度的變化規律如圖9 所示。 對于三種不同形貌的表面，接觸熱阻均隨壓力的增加而降低，并且降低速率變小，這與3.2 節的模擬結果吻合。 與此同時，接觸熱阻值在各壓力工況下，均隨表面粗糙度的增加而增加，可見高表面粗糙度是接觸熱阻存在的重要原因。

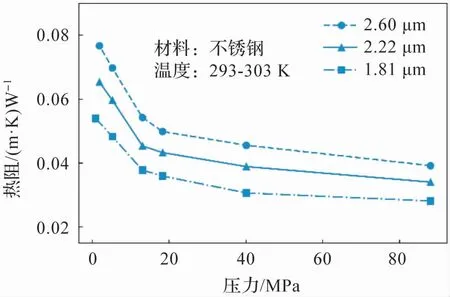
圖9 粗糙度對接觸熱阻的影響

4 結 論

（1）本文提出一種基于格子Boltzmann 方法預測曲面間接觸熱阻的模型。 本模型使用曲面坐標作為W-M 函數的參數生成接觸面分形形貌，使用塑性形變模型分析接觸面的形變特征，使用插值方法處理曲面邊界。 在計算有解析解的理想光滑曲面間隙熱阻模型時，得到較為準確的計算結果。

（2）研究結果表明：不同影響因子主要通過改變接觸面的間隙特征與間隙介質的導熱系數最終影響接觸熱阻的大小。 其中溫度主要影響間隙介質的導熱系數，壓力、材料和粗糙度影響接觸面的接觸特征。

（3）當間隙介質為空氣時，接觸熱阻隨溫度的升高緩緩降低。 高壓力，低硬度且表面光滑的材料，接觸更充分，接觸面間隙更小，其接觸熱阻往往更小。