求解機組組合問題的分段線性近似方法

全 然，張幼毅

（河南工業大學 理學院，鄭州 450001）

在電力系統中，機組組合(Unit commitment，UC)問題是一類重要的經濟調度問題，其數學模型是一類復雜的大規模混合整數非線性規劃（Mixed integer nonlinear programming，MINLP）問題[1]。該問題的主要目標是在滿足系統的功率需求和發電機組的技術要求條件下，使發電機組在計劃時間范圍內的總運行成本最低。

幾十年來，國內外專家學者在UC問題上已經提出了許多經典的求解方法，大致可分為兩類。第一類為數學優化算法，主要包括優先順序法(Priority list，PL)[2-3]、動態規劃法(Dynamic programming，DP)[4-5]、拉格朗日松弛算法(Lagrangian relaxation，LR)[6-7]、交替方向乘子 法(Alternating direction method of multipliers，ADMM)[8-9]、混合整數線性規劃法(Mixed integer linear programming，MILP)[10-12]等。第二類為智能優化算法，主要包括粒子群算法(Particle swarm optimization，PSO)[13-14]、模擬退火算法(Simulated annealing，SA)[15-16]、人工神經網絡算法(Artificial neural network，ANN)[17]等。數學優化算法屬于求解UC問題的經典算法，多年來在UC問題的求解上已得到廣泛應用。其中，DP法通過搜索機組的啟停狀態所形成的解空間以求解UC問題，能夠獲得中等規模UC問題的全局最優解；LR法將UC問題分解為一系列容易求解的子問題，能夠加快求解速度；MILP法是將UC問題近似為MILP模型進行求解，可在合理的時間內獲得高質量的次優解。智能優化方法也被廣泛應用于UC問題的求解，得到了較好的效果。然而，其有時容易出現早熟現象，導致解的質量不高。

MILP法已成為解決UC問題的主流方法，這主要歸功于MILP求解器算力的顯著改進。Carrión和Arroyo在文獻[10]中提出了UC問題的混合整數線性模型，需要較少的二進制變量和約束來減少計算負擔，獲得了良好的計算結果。在文獻[11]中，利用透視割平面逼近二次目標函數，所提MILP方法可在短時間內獲得高質量的解。文獻[12]通過引入一類新的有效不等式，對發電機的可行運行計劃給出了更緊的描述，從而顯著縮短了整體求解時間。文獻[18]提出了一種外內逼近（Outer-inner approximation，OIA）方法來求解UC問題。在這種OIA方法中，UC問題被分解為更緊的外逼近子問題和內逼近子問題，提供了更好的上下界。

分段線性近似（Piecewise linear approximation，PLA）是將非線性函數在其討論區間內用多段線性函數進行近似[19]。容易知道，增加斷點的數量將提高近似的精度，但會導致問題規模的增長，因此斷點數并不是越多越好；同時，斷點的選擇方法對求解的結果也有影響。文獻[19]通過對變量域進行不均勻劃分來選擇斷點，結果優于相同斷點數的均勻劃分。

本文利用PLA方法并對區域進行非均勻取點，將UC問題的MIQP模型轉化為MILP問題求解。仿真結果表明，與MIQP和區域均勻劃分取點的兩種方法相比，本文提出的方法能夠在一定程度上節約生產費用和計算時間，是一種有效的方法。

1 UC問題的數學模型

通常情況下，UC問題的數學模型為一個MIQP問題，具體如下。

（Ⅰ）目標函數

目標函數是使火電機組總燃料費用最小：

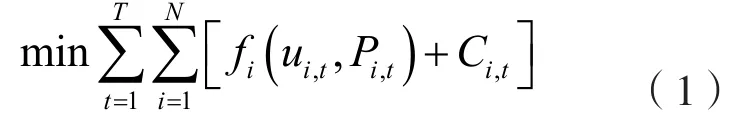
（Ⅱ）約束條件

（a）機組出力約束

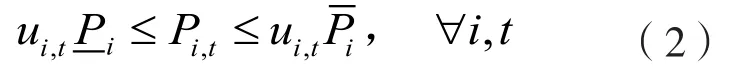
（b）系統的功率平衡約束

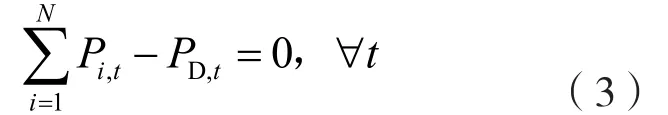
式中，PD,t為常數項，表示第t時段的功率總需求。

（c）系統的旋轉備用約束

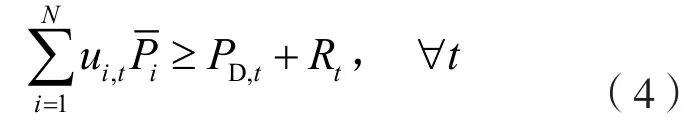
式中，Rt表示t時段的旋轉備用。

（d）機組的最小啟停時間約束

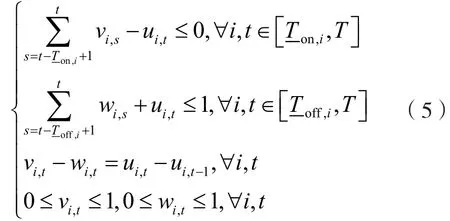
式中，vi,t，wi,t都是狀態轉移變量，如果機組i在t時段開機，則vi,t取值為1，否則值為0。與vi,t相反，機組i在t時段關機，wi,t取值為1，否則值為0。分別表示機組false的最小開機和停機時間。

（e）啟動費用約束

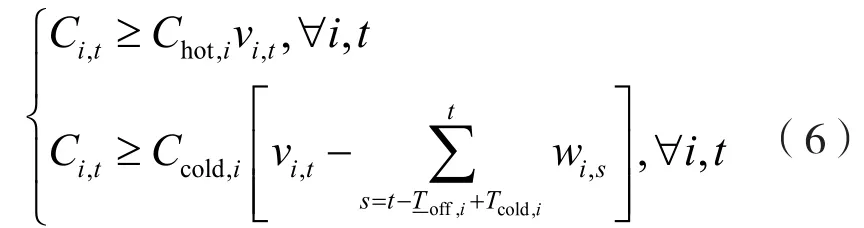
式中，Chot,i與Ccold,i分別表示機組i的熱啟動費用和冷啟動費用，Tcold,i表示機組i的冷啟動時間。

（f）機組出力的爬坡約束

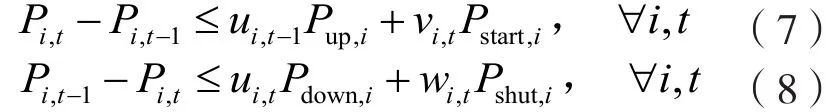
式中，Pup,i與Pdown,i分別表示機組i的功率上升速率限制和功率下降速率限制。Pstart,i與Pshut,i分別表示機組i的啟動功率速率限制和停機功率速率限制。

由前述可知，UC問題的數學模型為一個MIQP問題，具體為：

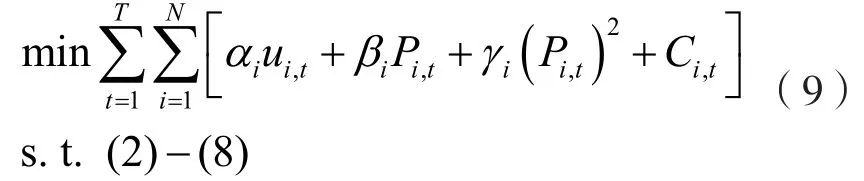
引入輔助變量ηi,t，則上述問題等價于

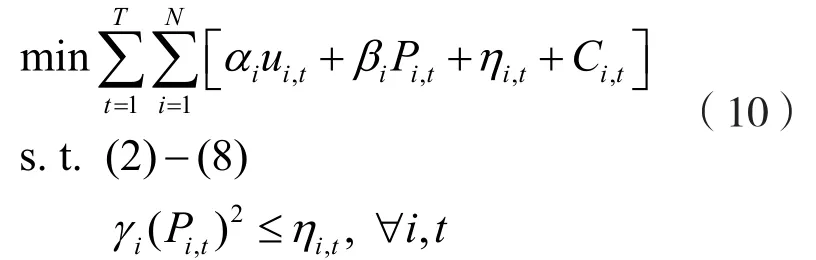
2 求解UC問題的PLA算法

下面介紹PLA的算法思想。設非線性函數f（x）在區間[xl, xu]上有定義，在[xl, xu]內插入 n-1 個斷點 x1, x2,…, xn-1，使得 x0= xl＜ x1＜x2＜…＜xn= xu，這 n-1個斷點將區間[xl, xu]分成 n個小區間 [xi, xi+1]，i=0,1,…,n-1。令 yi=f（xi）,i=0,1,…,n，則連接點（xi+1, yi+1）與（xi,yi）的線性函數構成了f（x）的分段線性近似，如圖1所示。

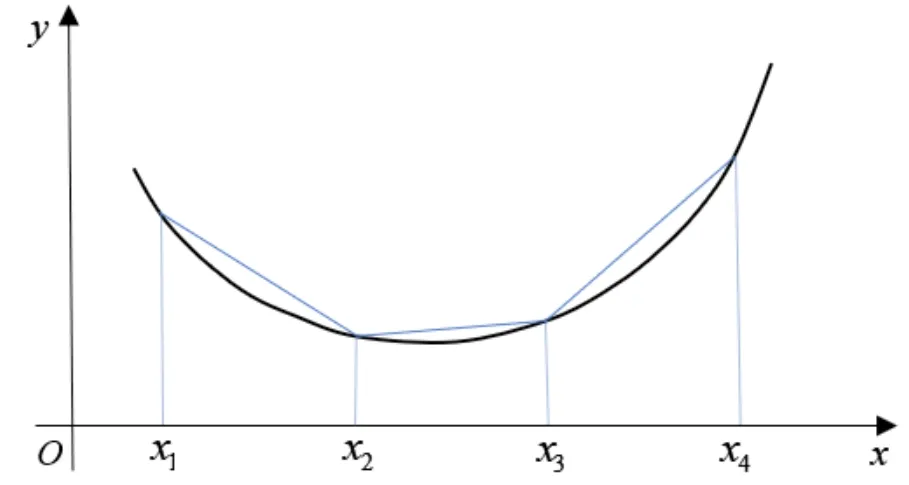
圖1 分段線性近似

容易知道，增加斷點的數量將提高PLA的近似精度，但也會導致問題規模的增長，這會給問題求解帶來一定的難度。為了提高近似精度，并控制問題的規模，本文采用區域的非均勻劃分方法[19]，具體方法如下。假設變量x∈[l,u]的局部解為x*，則可在區間[x*, u ]內或在[ l, x*]內選取斷點，本文采用文獻[19]中的非均勻斷點選取方法，即斷點取為：

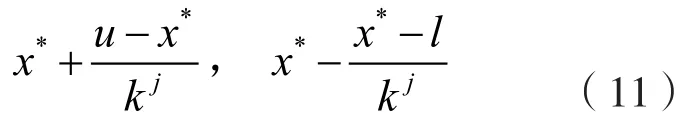
其中k取1到2之間的值，j=1,2,...。

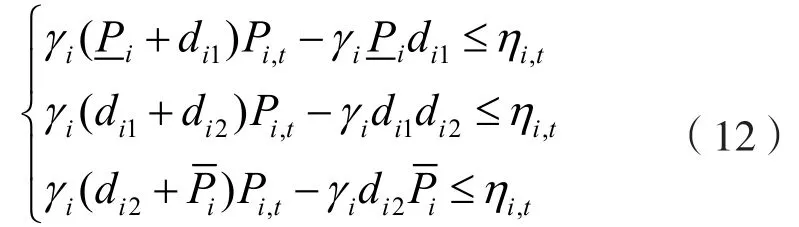
結合式，可得到UC問題的PLA模型：

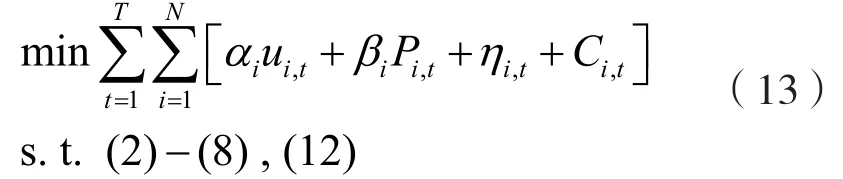
顯然，式是UC問題的一個MILP近似。

3 數值結果分析

3.1 參數設置

在MATLAB R2020a環境下進行編程，調用CPLEX 12.5對計算過程中涉及到的MILP、MIQP和二次規劃問題進行求解，MILP和MIQP的求解精度設置為10-3。計算機配置為：Intel(R)Core(TM) i5-7200U CPU @ 2.50 GHz 2.70 GHz。

本文在求解UC問題時，仿真的系統以10機組24時段系統為基礎，通過對此10個機組的數據復制可得到10個以上機組系統的數據。旋轉備用取系統總負荷的10%，即Rt= 0.1PD,t。計算時，考慮以下兩種情形的爬坡約束限制：情形一，爬坡出力速率限制和滑坡出力速率限制均取機組最大出力限制的20%，即；開機出力速率限制和停機出力速率限制均取機組最大出力限制，即。情形二，。

3.2 UC問題的計算結果

表1給出第一種情形下所提方法與另外兩種方法的計算結果比較。其中，OIA為外內逼近算法[18]，DEA為微分進化算法[20]。從表1可以看出，對于所有機組系統，所提方法均在一定程度上優于文獻中OIA和DEA這兩種計算方法。

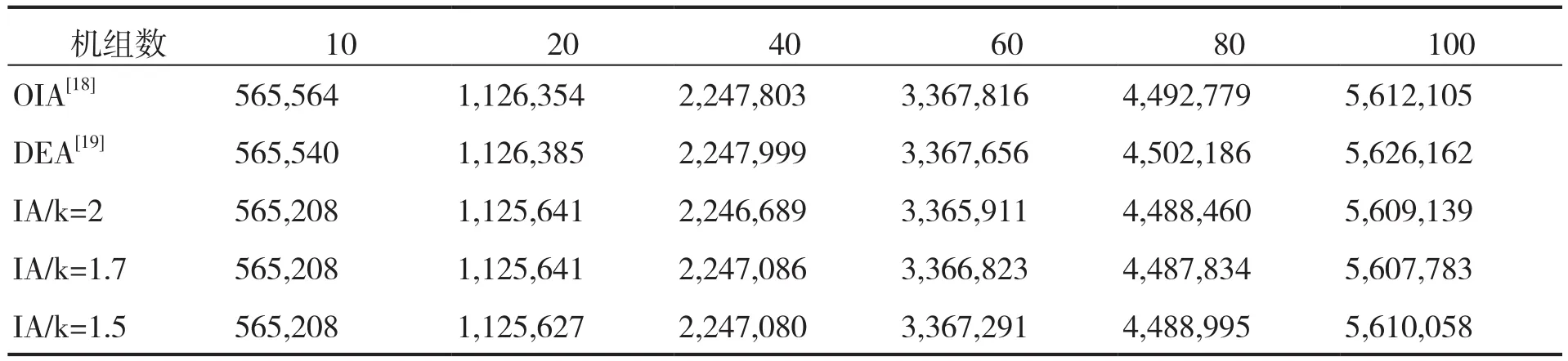
表1 不同算法總費用比較($)

表2為第一種情形下所提方法與均勻劃分的計算結果比較，第2列到第4列表示本文非均勻劃分的計算結果，第5列表示均勻劃分的計算結果。從表中可以看出，機組數為20、40、100時，非均勻劃分的次優值結果均在一定程度上優于均勻劃分。對于10機組系統，非均勻劃分與均勻劃分的次優值相等。對于60和80機組系統，均勻劃分和非均勻劃分的次優值各有優劣，但相差不大。對于計算時間，兩種劃分各有優劣，但對于k=2時的非均勻劃分，80和100機組系統用時較多。

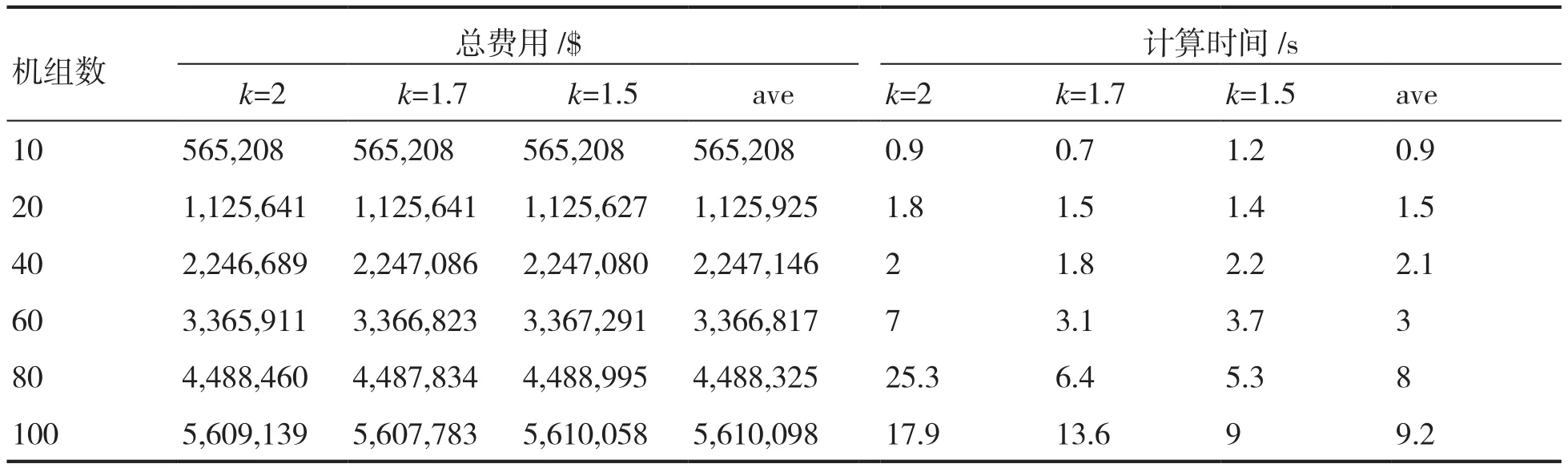
表2 情形一中本文方法與均勻劃分的計算結果比較

表3為第一種情形下所提方法與MIQP方法的計算結果比較。從表3可以看出，在次優值方面，兩種方法相差不大；但對于計算時間，所提方法明顯占優。

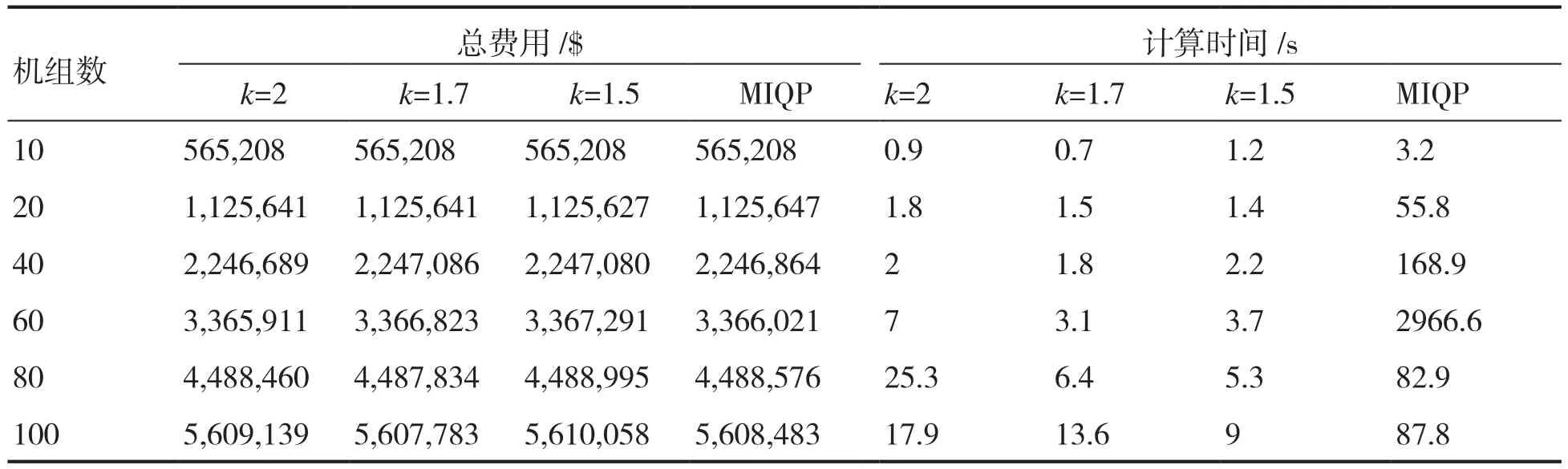
表3 情形一中本文方法與MIQP的數值結果比較

表4為第二種情形下所提方法與均勻劃分的計算結果比較。

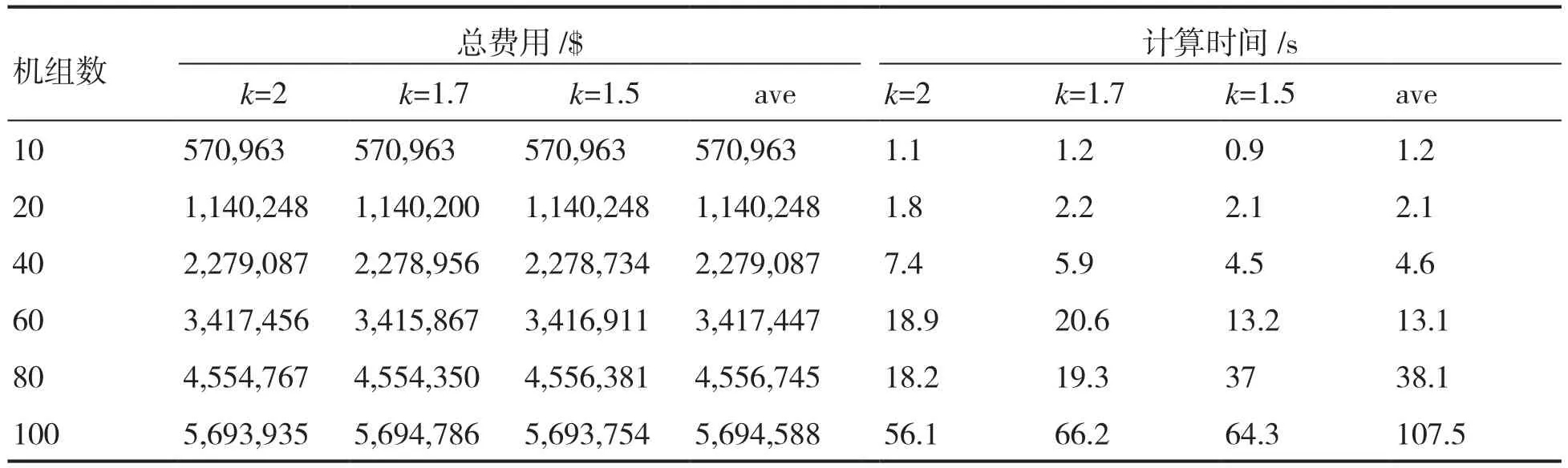
表4 情形二中本文方法與均勻劃分的計算結果比較

從表中可以看出，對于k=1.7時的非均勻劃分，20到80機組系統的次優值結果均優于均勻劃分。對于k=1.5時的非均勻劃分，當機組系統增加到40以上時，次優值結果均優于均勻劃分。對于10機組系統，非均勻劃分與均勻劃分的次優值相等。當k=2時，對于10到40機組系統，非均勻劃分和均勻劃分的次優值相等，對于60機組系統次優值相差不大，但對于80和100機組系統非均勻劃分的次優值優于均勻劃分。計算時間方面，對于10到60機組系統，非均勻劃分和均勻劃分兩者相差不大，但對于80和100機組系統，非均勻劃分的時間明顯占優。

表5為第二種情形下所提方法與MIQP方法的計算結果比較。對于60、80和100機組系統，所提方法在次優值方面比MIQP方法占有優勢，但兩種方法整體相差不大。對于計算時間，所提方法明顯占優。

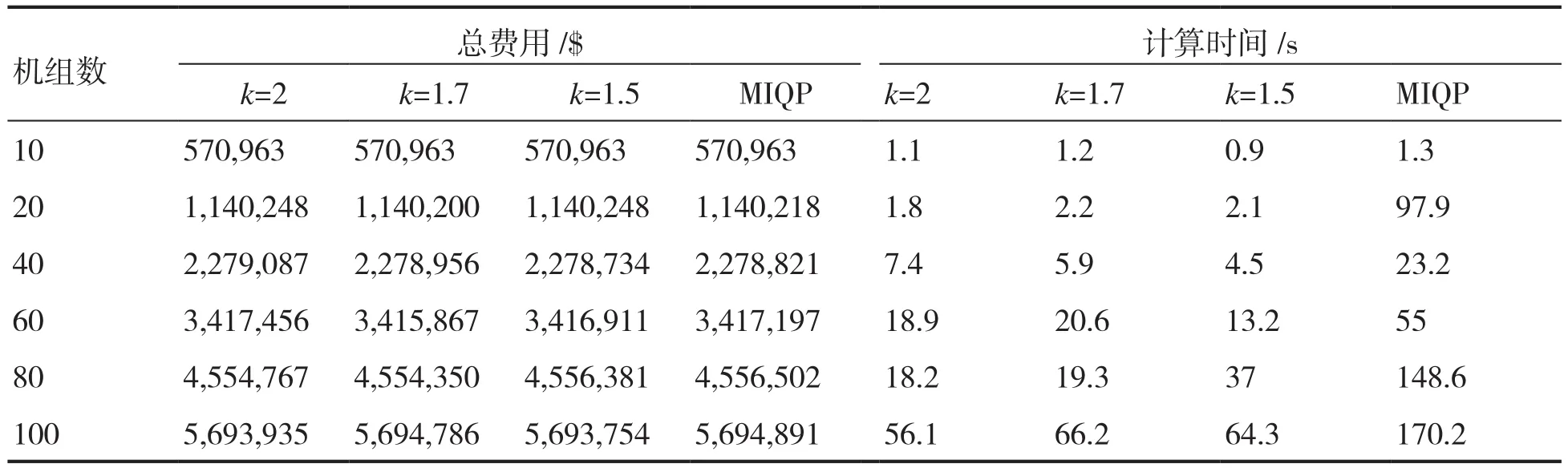
表5 情形二中本文方法與MIQP的數值結果比較

4 結論

本文利用PLA方法對區域進行非均勻取點，將UC問題轉化為MILP問題求解。數值結果表明，與MIQP方法和均勻取點方法相比，本文提出的方法能夠在一定程度上節約生產費用和計算時間，尤其是計算時間，具有良好的性能。