一道高考題的解法探究和問題深化
257051 山東省東營市勝利第二中學 王建敏 劉吉存
解析幾何中的定值問題歷來是高考的熱點、難點,它能有效考查學生的數學思維品質、關鍵能力和數學核心素養.如2021年全國新高考Ⅰ卷第21題就是一道背景新穎、內涵豐富的試題.筆者對這道題進行多角度探究.
1 試題呈現

(1)求C的方程;
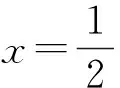
分析:本題以雙曲線為背景,考查定值問題.小問(1)是求有限制條件的雙曲線標準方程問題,比較基礎.小問(2)是在線段等積式條件下,求兩直線的斜率之和,是求隱含斜率和為定值的問題.幾何背景是圓錐曲線的四點共圓,結論是所成四邊形的對邊(不平行時)或兩對角線所在直線的傾斜角互補,當斜率均存在時,所在直線的斜率互為相反數,是直線與雙曲線的綜合題.本題主要考查了雙曲線的簡單性質及方程思想,還考查了計算能力及轉化思想、推理論證能力,考查學生的數學抽象、邏輯推理、數學運算、直觀想象、數學建模的核心素養.
2 解法探究
以下解法略去小問(1),只研究小問(2).


注:這是一種常規解法,利用弦長公式,借助韋達定理將線段問題轉化為直線斜率問題.求定值問題的常見方法有以下兩種.
(1)從特殊入手,求出定值,再證明這個值與變量無關.
(2)直接推理、計算,并在計算、推理的過程中消去變量,從而得到定值.
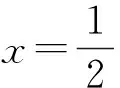
這里的二次項系數一定不為0,否則直線與雙曲線的漸近線平行,不可能與雙曲線有兩個交點.關于t的二次方程的判別式大于0?直線AB和直線PQ與雙曲線各有兩個交點?直線AB和直線PQ的斜率之和為0.
注:對于分點弦問題,基本的解題策略是利用直線參數方程中參數的幾何意義,理解|TA|,|TB|與t1,t2的關系,利用參數的幾何意義進行轉化并轉化為三角函數值進行計算,解答過程簡潔.

注:利用曲線系和四點共圓,再根據圓的方程的特征更快捷地得到結論.
3 問題深化
本試題源于人教版高中數學教材選修4-4第38頁例4:“AB,CD是中心為點O的橢圓的兩條相交弦,交點為P,兩弦AB,CD與橢圓長軸的夾角分別為∠1、∠2,且∠1=∠2.求證|PA|·|PB|=|PC|·|PD|.”此題所考查的實質就是圓錐曲線的四點共圓問題,是圓冪定理的逆定理的應用.
3.1 四點共圓的判定
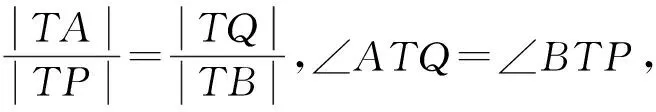

圖1圖2
3.2 m范圍的探討
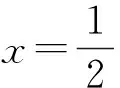
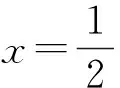

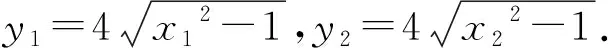
綜上所述,當且僅當點T的縱坐標m∈(-2,2)時,A,B,P,Q四點均存在,此時直線AB與直線PQ斜率之和為0.
3.3 一般化
3.3.1 問題拓展

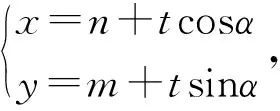
綜上所述,直線AB與直線PQ的斜率之和為0.反之,當直線AB與直線PQ的斜率之和為0時,借助同樣的思路可以證明|TA|·|TB|=|TP|·|TQ|.其中m,n只需滿足Δ=(32ncosα-2msinα)2-4(16cos2α-sin2α)(16n2-m2-16)>0即可,即m2-2mntanα+(n2-1)tan2α+16>0.

3.3.2 圓錐曲線上四點共圓的一般性結論與統一證明
定理若兩條直線y=kix+bi(i=1,2)與圓錐曲線ax2+by2+cx+dy+e=0(a≠b)有四個交點,則四個交點共圓的充要條件是k1+k2=0.
證明:兩條直線組成的曲線方程為(k1x+b1-y)·(k2x+b2-y)=0,則過四個交點的曲線方程可以設為(k1x+b1-y)·(k2x+b2-y)+λ(ax2+by2+cx+dy+e)=0 ①.
必要性若四點共圓,則方程①表示圓,則①式左邊展開式中xy項的系數為0,即k1+k2=0.

方程②的幾何意義是如下三種情形之一:表示一個圓、表示一個點、無軌跡.由題設知四個交點在方程②所表示的曲線上,故方程②表示圓.
注:(1)方程ax2+by2+cx+dy+e=0(a≠b)是對稱軸平行于坐標軸的圓錐曲線(圓除外)的統一形式,統一的證明必須有統一的表現形
式.從統一的思想高度來思考問題,必須求大同存小異,考慮共性的特征,否則,會陷入細枝末節中而不能自拔.本證法是數學形式化與數學本質的完美結合,證法簡潔、大氣,體現了數學的形式美、簡潔美與和諧統一之美.
(2)k1+k2=0是四點共圓的充要條件,λ是一個與k1,k2相伴隨的待定常數,只要存在這樣的常數使方程①表示圓即可.
上述定理用文字表述即為:斜率均存在的兩條直線與圓錐曲線有四個交點,則四個交點共圓的充要條件是兩直線的斜率互為相反數.這是一個非常簡潔的充要條件,運用這個定理可簡潔解決圓錐曲線上四點共圓的高考難題和數學問題.

