基于混沌序列的電力系統(tǒng)短期負荷預測

傅興吉，申艷偉，尹照洪，羅沖

（云南電網有限責任公司昆明供電局，云南 昆明 650000）

0 前言

對電力負荷進行準確預測關乎國家的穩(wěn)步發(fā)展和人民的幸福生活。本文以混沌理論和混沌預測方法等方面的內容作為主要的架構進行分析和研究，希望找到適應性和可靠性較好的短期負荷預測算法，從而獲得更好的預測精度和穩(wěn)定性，為制定電力計劃提供可靠的基礎數據。混沌主要是指存在于確定性系統(tǒng)中的無規(guī)則運動，只有具備相關特點的非線性系統(tǒng)才能產生混沌。利用混沌理論進行預測的主要思路就是將時間序列嵌入到重構的相空間中，從而讓新的狀態(tài)軌跡保留這原來的主要特征。利用混沌理論進行預測，只需要通過相空間重構就可以近似恢復原來的多維非線性混沌系統(tǒng)[1]，避免了其它多種繁瑣預測模型的建立，也不需要了解各種負荷與相應影響因素之間的任何關系。混沌理論預測一般包含時間序列混沌特性的判別、確定延遲時間與嵌入維數、重構相空間和預測4 個基本流程。

本文利用混沌相關理論對短期負荷進行預測，其主要思想結合歷史日負荷數據的混沌特性建立預測模型。大體思路如下：在獲取到一系列實際歷史負荷數據，并完成對負荷數據的處理后，對歷史負荷數據序列內部相關參數進行求解，從而完成混沌特性識別，同時根據求得的相關參數數據對相空間進行重構，最后，建立基于最大Lyapunov 指數預測模型，實現負荷預測。

1 混沌時間序列及相空間重構概念

1.1 混沌時間序列

時間序列是對連續(xù)時間信號進行采樣后得到的離散結果，混沌時間序列是一種特別的時間序列，它是由混沌的模型所產生的，具有與混沌一樣的類似隨機性，其動力學系統(tǒng)通常由系數確定的各類方程來描述。對于一個系統(tǒng)，我們必須對其是否混沌進行判斷。

系統(tǒng)中任何一個變量的時間演化都包含了它的其他變量長期演化的信息，因此，我們分析系統(tǒng)的混沌行為時可以將該單變量時間序列作為基礎。系統(tǒng)混沌時間序列中常用的幾個特征量及其對應的表征作用如下：關聯(lián)維反映了系統(tǒng)的復雜程度，Kolmogorov 熵反映了系統(tǒng)的混沌水平，Lyapunov 指數是系統(tǒng)混沌與否的關鍵，結合該指數的約束條件可以確定運動各階段的相關特性。

1.2 相空間重構理論

一個系統(tǒng)在某一時刻的狀態(tài)稱為相，決定狀態(tài)的狀態(tài)變量構成的幾何空間，稱為相空間[2]。系統(tǒng)中任意一個分量的演化都是由與之相互作用的其它分量所決定的，因此這些相關其它分量的信息就隱含在該任一分量的發(fā)展過程中[3]。只要將這一個分量在某些固定的時間延遲點上的測量作為新維處理，以之確定某個多維狀態(tài)空間中的一點，從而重構等價的狀態(tài)空間。經過不斷重復上述過程并測量各延遲時間的一個觀察量，經過正確的處理過程，就可以重構出原動力系統(tǒng)的模型。如下從數學上對Takens 定理進行介紹：

定義1：設(N,ρ)，(N1,ρ1)是兩個度量空間，如果存在映射φ:N→N1滿足：

1）φ滿射；

2）ρ(x,y)=ρ1(φ(x),φ(y))(Ax,y∈N)，則稱(N,ρ)，(N1,ρ1)是等距同構的。

定義2：如果(N1,ρ1)與另一度量空間(N2,ρ2)的子空間(N0,ρ2)是等距同構的，則稱(N1,ρ1)可以嵌入(N2,ρ2)。

Takens 定理：M是d維流形，φ:M→M，φ是一個光滑的微分同胚，y:M→R，y有二階連續(xù)導數，φ(x,y):M→R2d+1，其φ(x,y)=(y(x),y(φ(x)),y(φ2(x)),…,y(φ2d(x))，則φ(x,y)是M到R2d+1的一個嵌入。

按照Takens 定理就可以在拓撲等價意義下，對于某一個實測負荷數據時間序列{x(t),t=1,2,3,…,n}，根據選取的相關參量，就可以將時間序列對象拓展成如下m維相量：

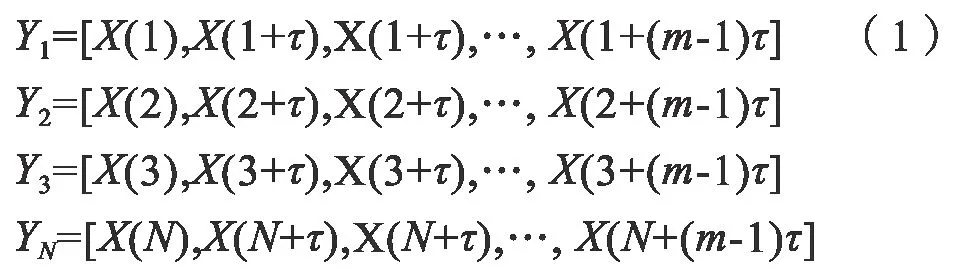
上式即為重構的相空間。其中，應當保證m≥2d+1，因為當嵌入維m＜2d+1 時，相空間就不能恢復原有性質；而當嵌入維數取值過大時，高維重構相空間將會包含過多的冗余信息，因此當嵌入維大于某個最大值時，預測精度會隨著嵌入維的增大而單調下降。而對于延遲時間的選取，當取值過小時，由于內部存在的一些原因將會使得信息不易顯露；當取值過大時，由于蝴蝶效應的影響，重構的相空間不能很好地反映整個系統(tǒng)的特性。相關基本參數延遲時間τ與嵌入維m的選取在重構相空間過程中非常重要，過大或過小都會使重構的相位空間無法顯示原始加載序列的動態(tài)。

2 短期電力負荷時間序列分析

2.1 整點負荷時間序列數據及預處理

本文獲取了某市電網20 個小時的整點電力系統(tǒng)負荷數據，序列長度為1460 個小時，如圖1 為該序列關于時間的二維曲線。本文用前1440 個整點負荷數據對后20 個整點負荷數據進行了預測。由獲取到的負荷時間序列可知在這1460 小時內，最大負荷為4953 MW，最小負荷為2828 MW。

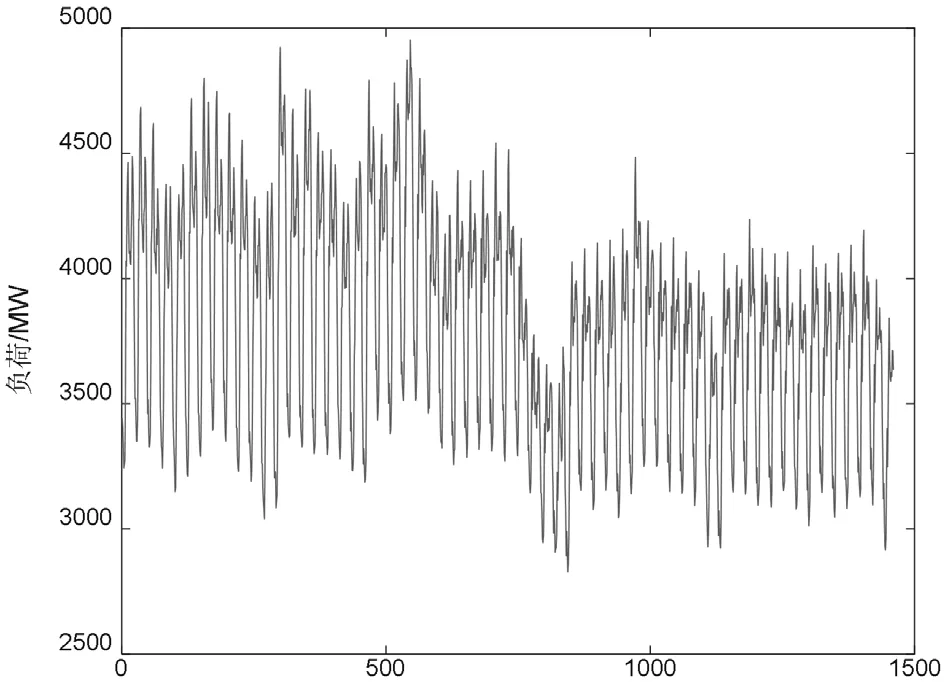
圖1 某市負荷時間序列曲線

在負荷預測中，數據的可靠性和易處理性是預測工作順利進行的關鍵，采用歸一化方法對獲取到的負荷時間序列數據進行預處理。

歸一化處理用到的公式如下：

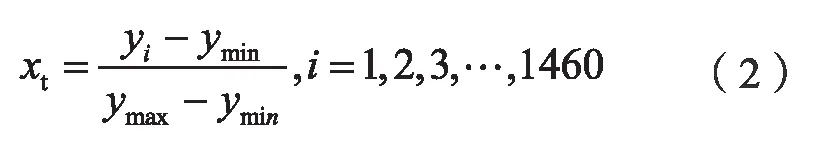
其中，通過查閱實際數據資料可知ymin=2828，ymax=4953，xt為負荷數據歸一化后的數據時間序列。對獲取到的數據進行歸一化處理后，得到的負荷時間二維圖形如圖2 所示：

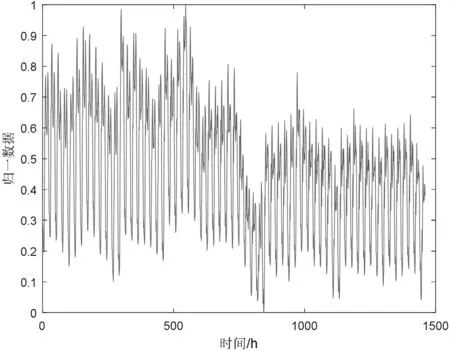
圖2 預處理后的序列曲線

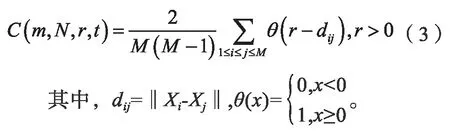
2.2 相空間延遲時間和嵌入維數選取

本文中，采用C-C 算法求延遲時間與嵌入維數：

設Xi=(xi,xi+τ,…,xi+(m-1)τ),Xi+∈Rm為重構的相空間，其中Xi(i=1,2,…,M)是重構相空間中的點，M=N-(m-1)τ，N為序列長度，m是嵌入維數，τ=t為延遲時間。定義該序列的關聯(lián)積分為[4]：

由于C-C 算法的研究與函數S(m,N,r,t)=C(m,N,r,t)-Cm(1,N,r,t)的值有關[5]。為了找到合適的延遲時間及更好的研究時間序列的動力學特性，需要先把整個時間序列分為t個子序列。如果t=1 時，為單個時間序列本身，而t=2 時為{x1,x3,…,xN-1}及{x2,x4,…,xN}，長度為N/2。對于一般的自然數有：

其中，N=tl，l=N/t是長度。對其它序列，將其分成t個不相交的子序列，然后將每個子序列的S(m,N,r,t)定義為：

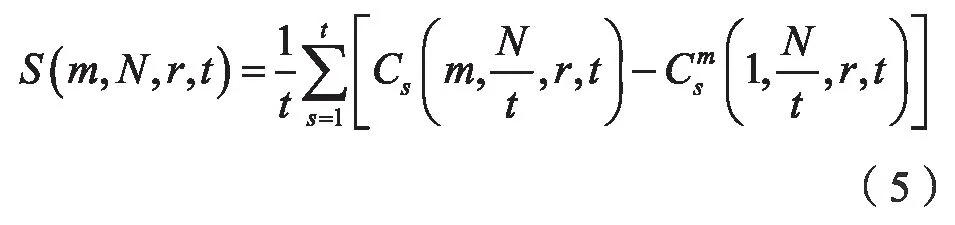
令N→∞，則有：

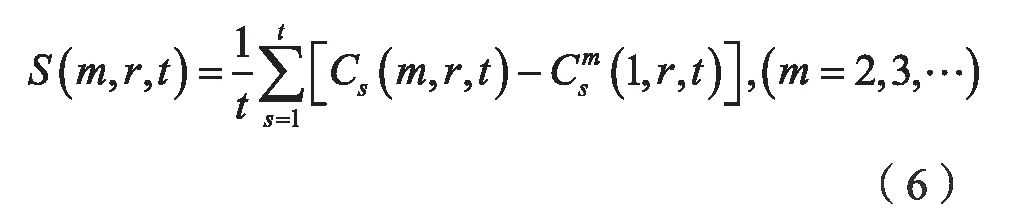
當N→∞時,對于所有的r,均有S(m,r,t)恒等于零。但實際的S(m,r,t)一般不等于零。這樣，局部最大時間間隔就可以取S(m,r,t)的零點或對所有的半徑r相互差別最小的時間點，因為這暗含著這些點幾乎是均勻分布的[6]。選擇對應值最大和最小半徑r,定義其差量為：

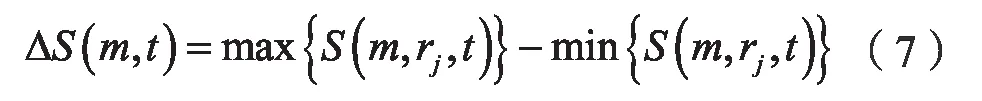
上式表示的是半徑的最大偏差。根據相關的統(tǒng)計結論，取m=2～5，ri=，i=1～4，通過計算以下3 式：

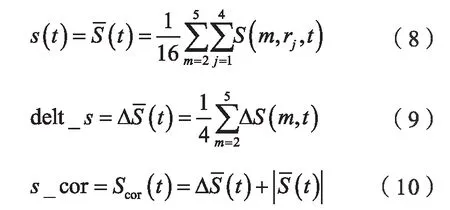
上式中，將s(t)的第一個零點對應的時間選為延遲時間τ，同時將s_cor 在時間區(qū)間中的最小值對應的時間作為時間序列的第一個整體最大時間窗口tw，然后就可以根據延遲時間與最大時間窗口的關系式tw=(m-1)*τ，從而確定嵌入維數m。

根據上述C-C 算法思想，用MATLAB 編程軟件進行編程調試，并將獲取到的負荷時間序列寫入程序中，運行C-C 算法程序后，得到的最大延時max_d與s(t)、delt_s、s_cor 三者之間的關系波形圖如圖3 所示。

圖3 C-C算法的輸出圖形

程序中最大延時max_d在1～18 之間取值。由圖可知s(t)的第一個零點對應的時間為3，因此將其選為延遲時間即τ=3，在相應時間區(qū)間內s_cor 取最小值時對應的時間為10 因此將其選為延時時間窗口即tw=10，延遲時間和最大時間窗口都確定以后，根據公式tw=(m-1)*τ，可以求得重構相空間的嵌入維數即得m=4.33，據相關資料顯示，重構相空間的最小嵌入維數一般向下取整，所以此處所取的嵌入維數為m=4。

2.3 最大Lyapunov指數

最大Lyapunov 指數不但是判斷系統(tǒng)混沌與否的重要條件，而且它還是確定可預測時長的關鍵參數。采用小數據量法，求解實測負荷數據序列的最大Lyapunov 指數。

假設混沌時間序列為x1,x2,…,xn，其他相關參數的符號表示方法與前面相同，則重構相空間可得到Y(ti)={x(ti),x(ti+τ),…,x(ti+(m-1)τ)}(i=1,2,…,N)，利用小數據量法計算最大Lyapunov 指數的具體思想如下：

1）利用C-C 算法同時算出嵌入維數m 和延遲時間τ。

2）根據實際所求得的重構參數，進行相空間重構后得{Yi|i=1,2,…,M}。

3）找到相空間中的每個點Yj和Yj，并進行限制短暫分離[15]，即：

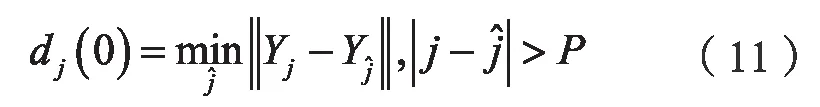
P為時間序列的平均周期[13]，本課題中我們獲取到的負荷時間序列，采用FFT 變換求得P=6。

4）對相空間中的每個點Yj，計算出該鄰點對的i個離散時間步后的距離dj(i)。

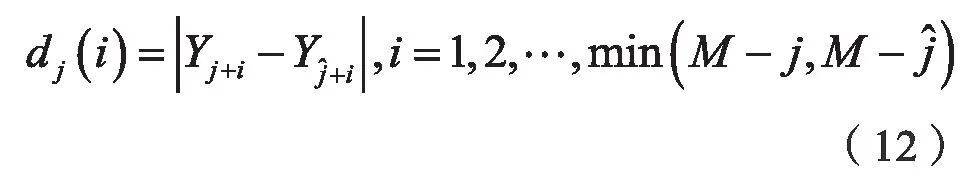
5）對每個i，求出所有j的lndj(i)平均y(i)，即：

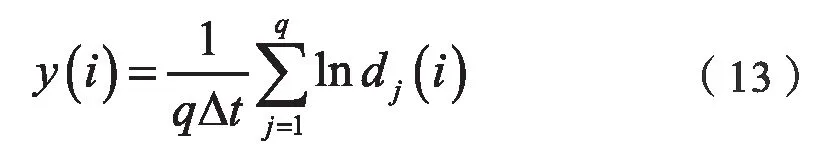
其中，q是非零dj(i)的數目，利用相關數學處理工具畫出其回歸直線，做出的回歸直線的斜率，小數據量法示意圖見圖4。

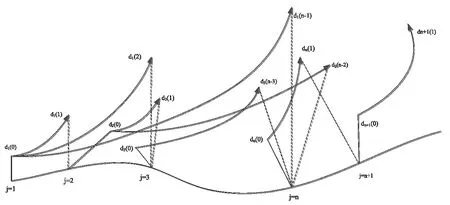
圖4 小數據量法示意圖

將2.2 中求得的相關參數τ=3、m=4，以及求得的時間序列的平均周期P=6 帶入到程序中，運行wolf 程序后，求得λ1=0.0506。由此，可以確定該負荷時間序列為混沌時間序列，同時可以確定最大可預測時間長度Tmax=1/λ1=19.763。

3 基于最大Lyapunov指數的預測模型構建

基于最大Lyapunov 指數建立模型的基本思想如下：對一維的混沌時間序列進行相空間重構后，設預測的中心點為XM，設Xk為XM在其相空間中的最鄰近點，二者的距離為dM(0)，其最大Lyapunov 指數為λ1，則：

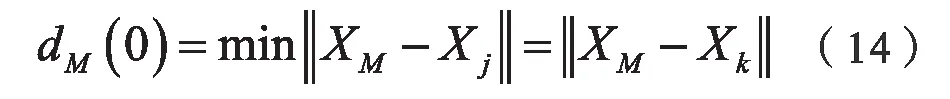
限制短暫分離，要求|M-j|＞P，其中P混沌時間序列的平均周期。結合如下最大Lyapunov 指數的定義

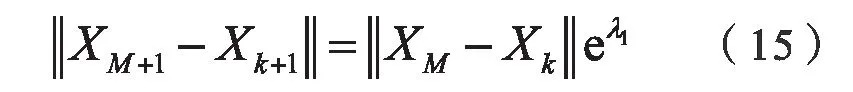
上式即為最大Lyapunov 指數預測模型[6]，該式子中，對于點XM+1只有最后一個元素分量未知，從數學方程求解來看是可求的，因此，未來一段時間的負荷是可以預測的。

該預測模型的具體算法思想如下[7]：

1）根據前文中求得的重構相空間的嵌入維數m和延遲時間τ，得到重構相空間：

2）結合前文，利用小數據量法計算各序列最大Lyapunov 指數λ1。

3）尋找中心點XM的鄰近狀態(tài)XK并計算d=‖XM-XK‖。

4）根據公式計算XM+1，并根據某種約定算法規(guī)則對根進行取舍。

5）將所得預測值帶入原序列中，重復上述步驟，直到預測完成。

3.1 預測模型可行性驗證

利用該預測模型對理論上的絕對混沌時間序列進行預測，從而判斷預測方法的可行性，分別采用Chen's 系統(tǒng)和Lorenz 系統(tǒng)的混沌時間序列進行驗證。

1）Chen's 系統(tǒng)驗證

Chen's 系統(tǒng)是一個經典的混沌系統(tǒng)[8]，其系統(tǒng)方程如下：

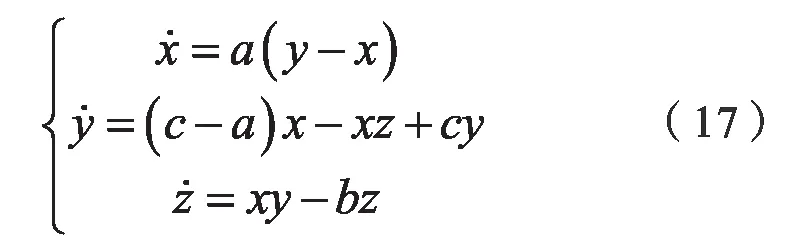
其中取a=35，b=3，c=28。

對于該混沌系統(tǒng)的x分量，用四階Runge-Kutta 法積分方程組，選擇積分步長T=0.001，參數延遲時間取10，嵌入維數取8，進行相空間的重構。利用本節(jié)提出的預測模型以前面4800個點對后面200 個點進行預測。其預測結果如圖5 所示，由預測結果曲線圖可知，該預測模型對Chen's 系統(tǒng)的混沌時間序列的預測效果良好。

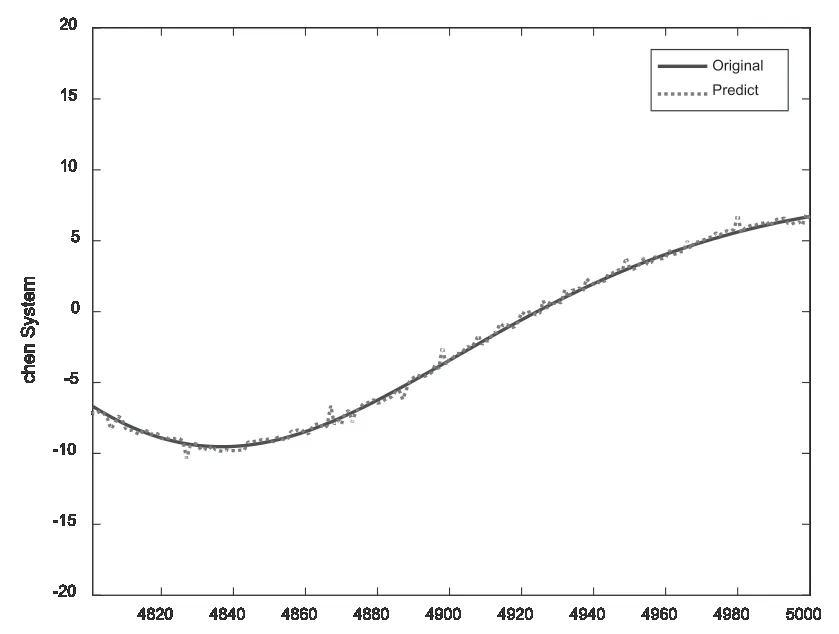
圖5 Chen's系統(tǒng)的混沌時間序列預測

2）Lorenz 系統(tǒng)驗證

Lorenz 系統(tǒng)方程如下：

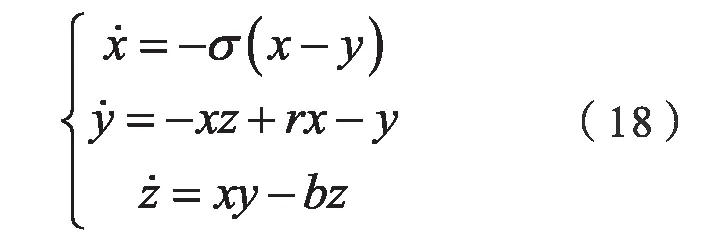
同樣，考察該混沌系統(tǒng)的x分量，用四階Runge-Kutta 法積分方程組，選擇積分步長T=0.001，參數延遲時間和嵌入維數分別取17和2，進行相空間重構后。利用最大Lyapunov指數的預測模型以前面4800 個點對后面200 個點進行預測。其預測結果如圖6 所示，由預測波形曲線圖可知，該預測模型對Lorenz 系統(tǒng)的混沌時間序列的預測效果良好。

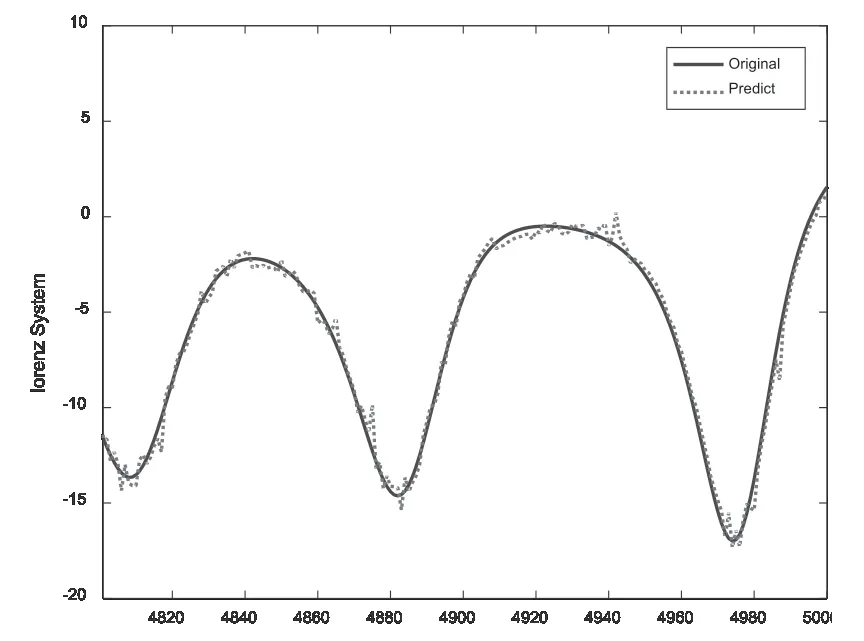
圖6 Lorenz系統(tǒng)的混沌時間序列預測

3.2 短期負荷預測模型仿真

Chen's 系統(tǒng)和Lorenz 系統(tǒng)兩者產生的混沌序列對最大Lyapunov 指數預測模型的驗證效果良好。利用該預測模型對鄭州市的整點電力負荷時間序列進行研究，時間序列一共1460 個數據，選取了某市2017 年3 月1 日到2017 年4 月30 日19 點的整點負荷，主要思路是以前1440 個數據為預測基準預測后面20 個點（即第1441 小時到1460 小時）的整點負荷進行預測。其中，相空間重構的參數先按照前述方法求得的，取τ=3，m=4，在程序中，對相關參數進行調試，直至找到最佳預測結果。運行程序后，得到的預測結果如圖7 所示。

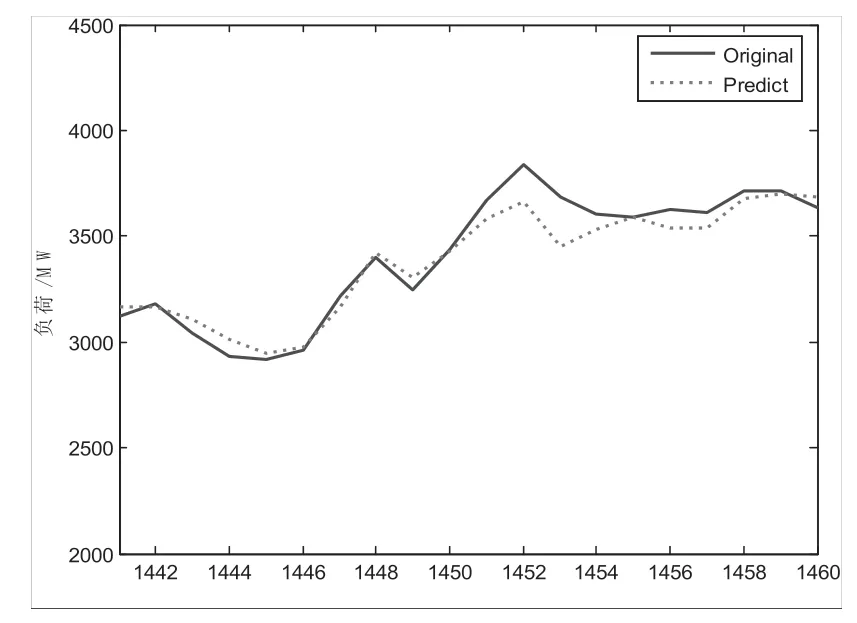
圖7 最大Lyapunov模型某市短期負荷預測

由預測曲線可以看出，基于最大Lyapunov指數的預測模型對鄭州市電網的短期負荷預測預測效果良好。另外，對于預測的誤差計算，我計算的是實際值與預測值二者之間的相對誤差，公式如下：

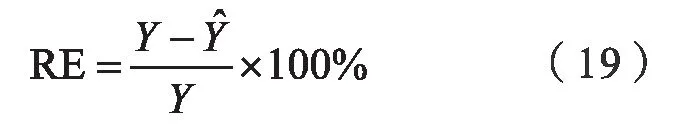
上式中，RE 為相對誤差，Y為實際值，為預測值。預測誤差曲線如圖8 所示。

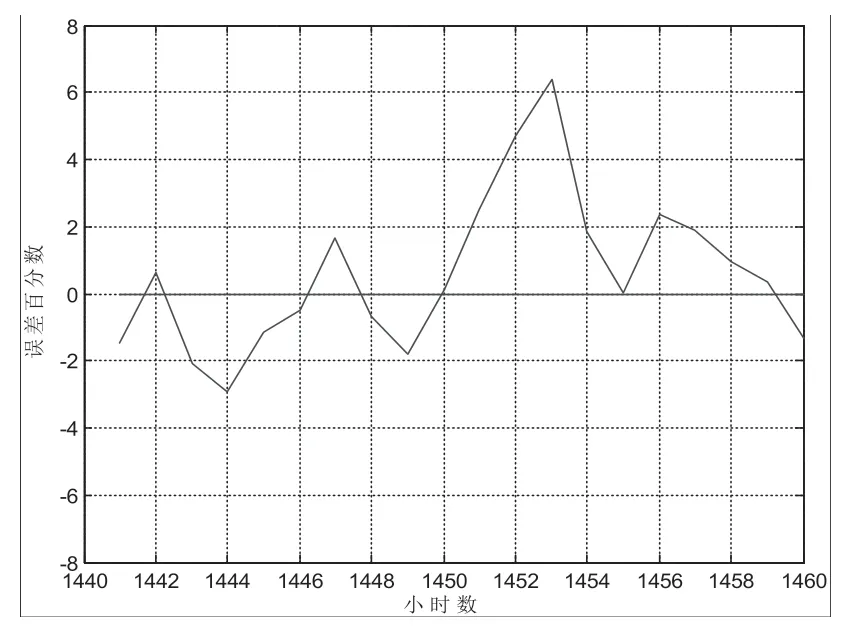
圖8 預測的相對誤差

由數據可知，預測誤差絕對值完全在7%以內，其中誤差在5% 以內的占95%，預測誤差的最大值為RE=6.374%，預測的最小誤差為RE=0.028%。由以上數據分析，可以看出這種預測模型預測出的數據基本滿足，預測精度很好。

4 結束語

本文基于混沌理論，采用C-C 算法對重構相空間的參數嵌入維數和延遲時間進行了求解，使用小數據量法求出最大Lyapunov 指數，最終建立了基于最大Lyapunov 指數預測模型，完成了對鄭州市2017 年4 月30 日0 點到19 點20 個整點負荷的預測，預測誤差絕對值都在7%以內。