問題驅(qū)動概念教學(xué)的實(shí)踐與反思
——以“等差數(shù)列前n項(xiàng)和”為例

丁永剛 (江蘇省徐州市第一中學(xué) 221140)

1 基本情況

1.1 授課對象

學(xué)生來自江蘇省四星級高中重點(diǎn)班，數(shù)學(xué)基礎(chǔ)較好，有一定的自學(xué)能力、邏輯推理能力和數(shù)學(xué)運(yùn)算能力．

1.2 課標(biāo)要求

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版)》(下稱《課標(biāo)2017》)指出：探索并掌握等差數(shù)列的前n項(xiàng)和公式，理解等差數(shù)列的通項(xiàng)公式與前n項(xiàng)和公式的關(guān)系；在數(shù)列教學(xué)過程中，可以組織學(xué)生閱讀數(shù)列方面的研究成果，尤其是我國古代的優(yōu)秀研究成果，感悟我國古代數(shù)學(xué)的輝煌成就．[1]

2 教學(xué)實(shí)踐

2.1 細(xì)心觀察，大膽猜想

問題1如何將下列古文“翻譯”成現(xiàn)代文？

今有與人錢，初一人與一錢，次一人與二錢，次一人與三錢，以次與之，轉(zhuǎn)多一錢，共有百人，問共與幾錢？——《張邱建算經(jīng)》

設(shè)計(jì)意圖通過中國北魏時期《張邱建算經(jīng)》中一道數(shù)學(xué)題導(dǎo)入所學(xué)內(nèi)容，引導(dǎo)學(xué)生通過觀察、討論、“翻譯”來發(fā)現(xiàn)問題中的等差數(shù)列，a1=1,a2=2,a3=3,…,a100=100，需求a1+a2+a3+…+a100．“翻譯”的過程滲透數(shù)學(xué)建模方法解決實(shí)際問題的思想，借此引出本節(jié)課的第一個概念：等差數(shù)列{an}前n項(xiàng)和定義：一般地，我們稱a1+a2+a3+…+an為等差數(shù)列{an}的前n項(xiàng)和，用Sn表示，即Sn=a1+a2+a3+…+an.回到古代的問題，轉(zhuǎn)化為數(shù)學(xué)語言，提出問題2．

問題2如何求1+2+3+…+100？

學(xué)生活動 分組討論首尾配對求和的原理和方法，討論高斯求和的精髓和局限性．

設(shè)計(jì)意圖適當(dāng)滲透數(shù)學(xué)史，了解數(shù)學(xué)家 的故事．高斯求和的精髓在于首尾配對，體現(xiàn)了消項(xiàng)的思想，下面利用高斯求和法研究一個實(shí)際問題．

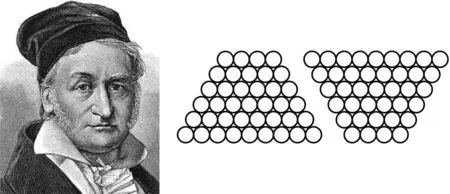
圖1 高斯 圖2

問題3怎樣計(jì)算圖2中鋼管的總數(shù)？

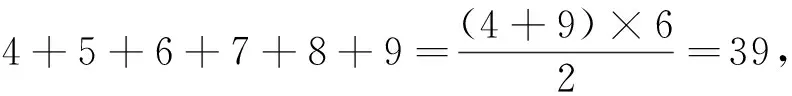
問題4如何求1+2+3+…+n？

學(xué)生活動 小組討論，如何求和？

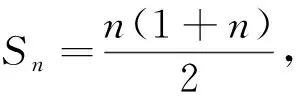
問題5猜想等差數(shù)列前n項(xiàng)和Sn=a1+a2+…+an的計(jì)算公式．

學(xué)生活動 思考并猜想結(jié)果能否與實(shí)際問題一致．

設(shè)計(jì)意圖由問題4類比推理問題5，引發(fā)學(xué)生合理猜想，接著肯定學(xué)生的猜想，猜想出的結(jié)論需經(jīng)過嚴(yán)格的證明，從而引出下一環(huán)節(jié)“合作探究，嚴(yán)格證明”．

2.2 合作探究，嚴(yán)格證明

問題6如何證明等差數(shù)列的前n項(xiàng)和公式？

學(xué)生活動 討論一般情況下的等差數(shù)列如何推導(dǎo)求和公式，嘗試總結(jié)公式的記憶方法．

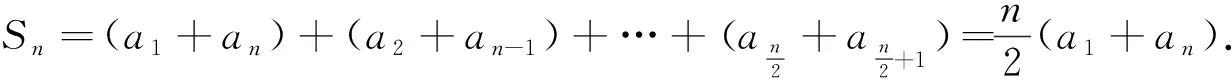
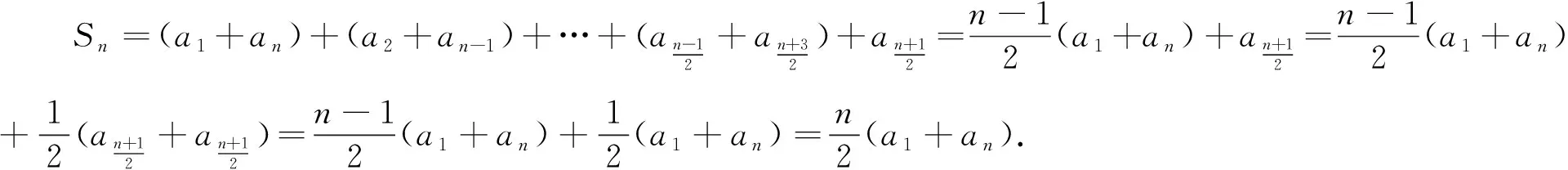
問題7審視問題3解法中兩幅圖與解法的關(guān)系，能否避開分類，重新證明問題6？

設(shè)計(jì)意圖為“倒序相加法”的出現(xiàn)做鋪墊．

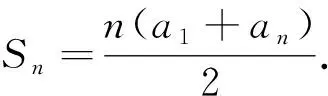
師：生2將數(shù)列中的每一項(xiàng)都用基本量首項(xiàng)a1、公差d表示，這是研究等差數(shù)列問題的通法，將數(shù)列通項(xiàng)的順序顛倒后相加實(shí)現(xiàn)等差數(shù)列的求和．

問題8如何改進(jìn)生2的證法，使之更簡潔？

設(shè)計(jì)意圖倒序相加已經(jīng)呈現(xiàn)，但需要再次簡化過程．

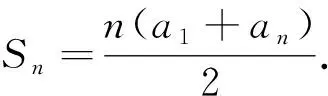
師：生3的證法更簡潔直觀，當(dāng)數(shù)列首末兩項(xiàng)的和a1+an為常數(shù)時，常用倒序相加法求數(shù)列的和，如何記憶此公式？

生4：借助梯形面積公式記憶更牢固.

設(shè)計(jì)意圖小組討論，學(xué)生多人合作終于完成證明過程，可以讓學(xué)生感受倒序相加法的形成過程和使用條件，學(xué)生總結(jié)公式的記憶方法，完成知識建構(gòu)．

2.3 新知初學(xué)，牛刀小試

問題9在等差數(shù)列{an}中，an=2n-1，求Sn．(結(jié)果用n表示)

學(xué)生活動 學(xué)生以搶答的方式進(jìn)行，口述解題過程與結(jié)果．

設(shè)計(jì)意圖讓學(xué)生體會公式的簡單運(yùn)用，小試牛刀，提升學(xué)習(xí)的熱情．

2.4 師生合作，公式運(yùn)用

問題10等差數(shù)列{an}中：

(1)已知a1=3，a50=101，求S50；

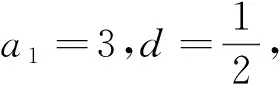
學(xué)生活動 學(xué)生回答解題思路與過程，教師黑板板演完整解題過程．

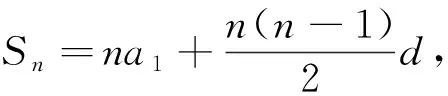
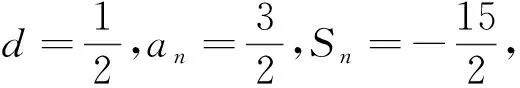
學(xué)生活動 學(xué)生在草稿紙上書寫解題過程，教師利用投屏技術(shù)，展示學(xué)生完整解題過程，讓學(xué)生講解思路，鼓勵學(xué)生一題多解．

設(shè)計(jì)意圖本題是等差數(shù)列求和公式的逆向運(yùn)用，訓(xùn)練學(xué)生逆向思維能力．

問題12已知等差數(shù)列{an}，填寫下表：

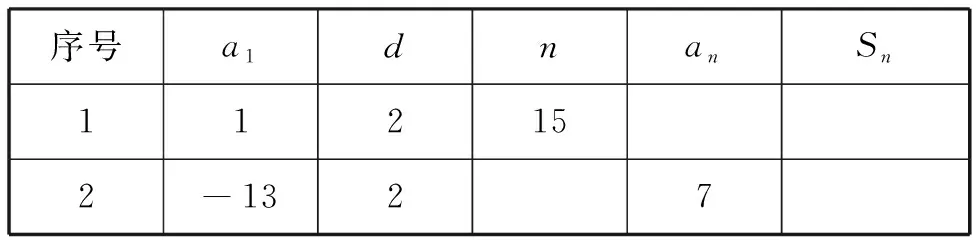
序號a1dnanSn112152-1327

學(xué)生活動 學(xué)生以小組為單位進(jìn)行搶答．

設(shè)計(jì)意圖此題是對于求和公式“知三求二”的鞏固練習(xí)．

問題13在等差數(shù)列{an}中，已知第1項(xiàng)到第10項(xiàng)的和為310，第11項(xiàng)到第20項(xiàng)的和為910，求第21項(xiàng)到第30項(xiàng)的和．

學(xué)生活動 學(xué)生先獨(dú)立完成，然后小組討論，利用投屏技術(shù)展示完整解法．引導(dǎo)學(xué)生深入思考：此題除了基本量法之外，還有別的解法嗎？

設(shè)計(jì)意圖此題是公式的靈活運(yùn)用，將題目條件化為基本量，這是解數(shù)列題的通法，強(qiáng)調(diào)通性通法.本題體現(xiàn)了化歸轉(zhuǎn)化思想，尊重學(xué)生思維發(fā)展的廣度，鼓勵創(chuàng)新解法．

2.5 課堂檢測，鞏固新知

問題14在等差數(shù)列{an}中，an=2n+3，Sn=an2+bn+c(a,b,c是常數(shù))，求a-b+c．

學(xué)生活動 通過抽簽抽取學(xué)生答題，小組內(nèi)部可提供幫助，10秒鐘內(nèi)若沒有思路則重新進(jìn)行抽簽．

設(shè)計(jì)意圖本環(huán)節(jié)為課堂檢測環(huán)節(jié)，通過控件抽簽器(利用Int函數(shù)，抽取隨機(jī)數(shù))抽取學(xué)生來答題，為求和公式性質(zhì)的學(xué)習(xí)做鋪墊，以此方式調(diào)動學(xué)生的學(xué)習(xí)興趣，提高課堂學(xué)習(xí)的效率．問題9讓學(xué)生初次體驗(yàn)計(jì)算成功的喜悅，問題10～12是公式的正用、逆用、變形用，層層推進(jìn)，讓學(xué)生感受數(shù)學(xué)解題中的變化．

2.6 小結(jié)提升，反思升華

問題15本節(jié)課你學(xué)到了哪些知識與技能、過程與方法？

3 教后反思

本課的授課對象整體水平較高，整個教學(xué)過程基本與課前預(yù)設(shè)一致，達(dá)到了預(yù)期的教學(xué)效果．

3.1 內(nèi)容響應(yīng)課標(biāo)，突出重點(diǎn)

《課標(biāo)2017》指出：在教學(xué)中可以組織學(xué)生收集、閱讀數(shù)列方面的研究成果，特別是我國古代的優(yōu)秀研究成果……感悟我國古代數(shù)學(xué)的輝煌成就．[1]本節(jié)課設(shè)計(jì)用到中國古代數(shù)學(xué)家張邱建的著作《張邱建算經(jīng)》與高斯求和等數(shù)學(xué)文化內(nèi)容，特別突出張邱建的研究，讓學(xué)生體驗(yàn)深厚的民族自豪感．教學(xué)設(shè)計(jì)凸顯數(shù)學(xué)建模、邏輯推理、數(shù)學(xué)運(yùn)算等數(shù)學(xué)學(xué)科素養(yǎng)的培養(yǎng)指向，在教學(xué)目標(biāo)達(dá)成的同時，傳遞給學(xué)生數(shù)學(xué)學(xué)習(xí)的必備品質(zhì)、學(xué)習(xí)能力和正確的價(jià)值觀念．

本節(jié)課的教學(xué)重點(diǎn)在于公式的推導(dǎo)，在問題3和問題4中讓學(xué)生充分感受高斯首尾配對算法的局限性，通過教材上的實(shí)例，感受倒序相加法的巧妙之處，從而在公式推導(dǎo)過程中自然呈現(xiàn)．本節(jié)課的教學(xué)難點(diǎn)在于公式的運(yùn)用，問題9到問題12均為對公式的運(yùn)用．在問題10第(2)題中，將通項(xiàng)公式代入求和公式，可引出本節(jié)課的第二個求和公式，通過對兩個公式與通項(xiàng)公式的分析，發(fā)現(xiàn)共有5個量，可“知三求二”．問題12為趣味競答環(huán)節(jié)，設(shè)置控件抽簽器，抽取學(xué)號，由學(xué)生現(xiàn)場抽題，激發(fā)了學(xué)生課堂學(xué)習(xí)的樂趣．

3.2 問題驅(qū)動探究，訓(xùn)練思維

數(shù)學(xué)是思維的科學(xué)，而問題是數(shù)學(xué)的心臟，語言是思維的外殼．布魯納說過：“教學(xué)過程是一種提出問題和解決問題持續(xù)不斷的活動，思維永遠(yuǎn)是從問題開始．”本節(jié)課共設(shè)計(jì)了15個問題組成問題串(有預(yù)設(shè)的問題，也有生成的問題，如問題7和問題8)，問題1讓學(xué)生對等差數(shù)列前n項(xiàng)和的概念產(chǎn)生直覺猜想，問題2解決問題1提出的問題，問題3是問題2的特殊情況，問題4是從問題2、問題3的特殊情況到一般情況，問題5是問題4的更一般情況，問題6到問題8是對問題5的證明過程的層層改進(jìn)，為引出“倒序相加求和法”做鋪墊，由此獲得對“倒序相加求和法”的本質(zhì)的認(rèn)識，可謂是精心設(shè)計(jì).問題13和問題14是公式的靈活應(yīng)用，體現(xiàn)了公式的應(yīng)用價(jià)值，問題15有效地促進(jìn)學(xué)生反思，在總結(jié)知識、升華內(nèi)容的同時，有效培養(yǎng)了學(xué)生的理性思考和概括能力.15個高質(zhì)量的問題驅(qū)動學(xué)生對等差數(shù)列前n項(xiàng)和的求和公式進(jìn)行了深入的探究，由此獲得對等差數(shù)列求和公式的本質(zhì)認(rèn)識，在問題串的驅(qū)動下，數(shù)學(xué)建構(gòu)、數(shù)學(xué)探究過程嚴(yán)謹(jǐn)而又流暢，在潛移默化中訓(xùn)練了學(xué)生的思維能力．

3.3 過程引領(lǐng)發(fā)展，提升素養(yǎng)

學(xué)生經(jīng)歷“觀察—猜想—證明—運(yùn)用”的探究過程，探究等差數(shù)列前n項(xiàng)和公式的多種證明方法，通過古代數(shù)學(xué)問題發(fā)現(xiàn)了數(shù)列求和，繼而提出如何求等差數(shù)列前n項(xiàng)和，通過小組合作，得出等差數(shù)列的前n項(xiàng)和公式.此過程中，學(xué)生發(fā)現(xiàn)問題、提出問題、分析問題、解決問題的能力得到培養(yǎng)，其從特殊到一般的邏輯推理能力得到訓(xùn)練，教師引領(lǐng)學(xué)生走上了科學(xué)研究的正確道路，提升了學(xué)生的學(xué)科核心素養(yǎng)．

3.4 知識表征多樣，促進(jìn)建構(gòu)

20世紀(jì)80年代美國數(shù)學(xué)教育學(xué)家杜賓斯基提出了一種關(guān)于數(shù)學(xué)概念教學(xué)的APOS理論，該理論的主要觀點(diǎn)是：學(xué)生學(xué)習(xí)數(shù)學(xué)概念就是心智結(jié)構(gòu)建構(gòu)的過程，具體可分為操作階段、過程階段、對象階段和圖式階段．以此理論為出發(fā)點(diǎn)，本節(jié)課在設(shè)計(jì)教學(xué)流程時重視如何使學(xué)生在心智建構(gòu)過程中發(fā)揮較好的主體作用．為此，筆者在設(shè)計(jì)教學(xué)過程時，向?qū)W生提供了圖形、文字、符號等多樣化的知識表征，創(chuàng)造出靈活變化的教學(xué)情境，激發(fā)學(xué)生的數(shù)學(xué)思考，給學(xué)生創(chuàng)造探索數(shù)學(xué)規(guī)律、發(fā)現(xiàn)數(shù)學(xué)本質(zhì)的機(jī)會，使教學(xué)活動開展得富有成效，從而將探究式學(xué)習(xí)得到落實(shí)與推進(jìn)[2]．

3.5 知識鼓勵應(yīng)用，升華思想

在引導(dǎo)學(xué)生探索并證明等差數(shù)列前n項(xiàng)和公式之后，筆者還啟發(fā)學(xué)生利用公式解決相關(guān)數(shù)學(xué)實(shí)際問題，體會和挖掘數(shù)學(xué)公式在解決實(shí)際問題中的作用．筆者一方面設(shè)計(jì)了配套的題組，使學(xué)生熟練掌握公式并加深對公式的理解；另一方面從形式上、結(jié)構(gòu)上引導(dǎo)學(xué)生思考除了“知三求二”還有哪些應(yīng)用與推廣，隨著后續(xù)章節(jié)的不斷推進(jìn)，學(xué)生會在后續(xù)學(xué)習(xí)中不斷領(lǐng)會知識應(yīng)用中滲透的相關(guān)數(shù)學(xué)思想[3]．