順“思”而為 借“思”而上
——三個數學案例的實錄、評析和思考*
章祥俊 (江蘇省蘇州吳縣中學 215129)
近年來,數學課堂的變化是巨大的,課堂教學過程中的問題驅動、活動引領、任務驅動、項目學習、單元設計等已經成為趨勢.課堂教學中,以學生為中心,關注學生動手實踐、自主探究、合作交流、問題解決等已經成為常態.[1]課堂教學中,我們應更多地關注學生的自主空間,關注學生的主動學習,關注學生的主體意識,實現學生的自我價值,激發學生的學習動力,順勢而為,借思而上,引導學生深度思考,促進學生學會學習.本文擬結合三個案例具體談一談.
1 順“思”而為,引發自主探究,促進學生主動學習
案例1求函數f(x)=x2-2x-3,x∈R的最小值.
生:因為f(x)=x2-2x-3=(x-1)2-4,所以函數f(x)的最小值為f(1)=-4.
設計問題 以二次函數為背景,請你命制一道求函數最值的題目.
生1:求函數f(x)=x2-2x-3,x∈[2,3]的最小值.
生2:求函數f(x)=x2-2x-3,x∈(2,3)的最小值.
生3:求函數f(x)=x2-2x-a,x∈[2,3],a∈R的最小值.
生4:求函數f(x)=x2-ax-3,x∈[2,3],a∈R的最小值.
生5:求函數f(x)=ax2-2x-3,x∈[2,3],a∈R的最小值.
生6:求函數f(x)=x2-2x-3,x∈[a-1,a+1],a∈R的最小值.
生7:求函數f(x)=ax2-2ax-3,x∈[2,3],a∈R的最小值.
生8:求函數f(x)=ax2-bx+c,x∈[m,n],a,b,c,m,n∈R的最小值.
評析和思考以二次函數為背景的函數最值問題是高一數學學習中一個重點內容.教師在進行教學設計時,將預設的題目變為引導學生自行研究、小組討論、解題和歸納的開放題,讓學生自己命制求函數最值的題目,順著第一個學生的思維,組織學生進行自編活動,共編制出8個變式題.通過這樣順“思”而為的活動引導學生主動思考與探究,思維層層遞進,將二次函數從“定軸定區間”的研究自然深入到“動軸定區間”“定軸動區間”“動軸動區間”的研究.在這樣的過程中,學生的思維因問題的開放性和探究性而激活,教學效果必然好很多,同時,這樣處理極大地調動了學生的積極性和主動性.從培養學生數學觀念的角度看,這樣的過程可以培養學生在一定的數學情境中抽象出數學概念、命題、方法和體系,積累從特殊到一般的活動經驗、從靜止到變化的函數思想方法,養成在日常學習和實踐中從一般性角度思考問題的習慣,把握事物的本質,以簡馭繁,運用數學思維思考并解決問題.順“思”而為激發了學生的主動學習,實現了學生的思維升華,提升了學生核心素養發展,促進了學生的主動學習.
2 借“思”而上,探究知識本質,促進學生樂于學習
案例2等比數列前n項和Sn=a1+a1q+a1q2+…+a1qn-1公式的推導.
生1:提取公因數a1.
生2:倒序加?倒序乘?
生3:特殊化,令Sn=1+2+22+…+2n-1,猜想Sn=qn-1.
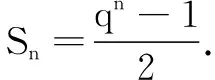
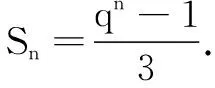
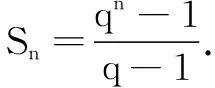

評析和思考很多教師在推導等比數列前n項和公式時將“錯位相減法”硬塞給學生,學生表面上聽懂了,但他們心中的“惑”由誰人來解?學生是在多次操練下似懂非懂地練“會”了,這是真的會了嗎?他們理解為什么這樣推導嗎?學生對錯位相減法的道理感覺云里霧里,整個學習處于被動的狀態.
在講授該內容時,筆者曾遇到這樣的情景:先問學生如何進行推導,得到的回復是“我不會”,也有回答“錯位相減法”的、再追問時得到的回答是“課本上就是這樣”,然后順著學生的回答講授該方法,學生也就被動地聽之.直到兩年前,同樣講授該內容時,遇到一個“固執”的學生追問“為何如此推導”,且有不達目的不罷休之勢,借著這位學生的“思”引導全班學生共同思考、探究,把順勢和借思的時間給足學生,終得上述案例2.
筆者曾做過多次調查,讓高三的學生證明課本中一些定理、公式時,能證明或推導出的學生寥寥無幾.課程改革致力于培養學生的核心素養、關鍵能力和終身學習的學習力,其出發點和根本目的是完全正確的,但是在教學實踐中很多教師還是“新瓶裝舊酒”,教學中僅僅關注“是什么”而忽視“為什么”,這不得不令人深思.實際教學中,我們完全可以把課堂真正讓給學生,把思考的時間和機會留給學生,讓學生借“思”而上.通過自己的理解和與同伴的交流討論,學生一定能理解“錯位相減法”的本質,其學習的興趣也就自然被激發出來了.
3 因“思”利導,提升思維品質,促進學生深度學習
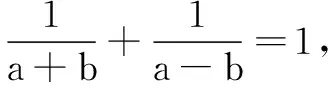
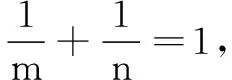

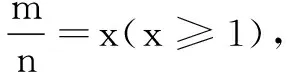
生5:也不對!因為當x=1時,m=n,即a+b=a-b,于是b=0,與已知條件矛盾.
生7:可以將題目改為求3a+2b的取值范圍.
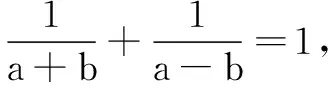
評析和思考在該案例中,從高考常考的多元最值問題出發,引導學生對問題進行多維的探究與反思,思維在交流碰撞中提升,真正理解了問題的處理方法.學生經歷由通性通法研究到錯誤引發的思維過程,再到找到原因、變式研究,有效地鞏固了數學知識、訓練了解題方法、提升了解題技能、滲透了數學思想方法、提高了探究能力,這就是培養學生核心素養和關鍵能力的有效途徑.高中數學知識方法千萬條,但數學理解是第一條.課堂教學應立足于學生的“最近發展區”,以學生的眼光組織開展數學教學,最大限度地促使學生學會數學思考,提高數學思維的參與度.[2]
4 結語
在課堂教學中,我們不能只“授業”,而不“解惑”;不能只訓練方法,而忽視能力的提升;不能只關注遠方,而忽略了腳下行走的路;不能只關注“正確的”,還要多關注那些“錯誤的”;不能“硬塞給”學生,而應該吸引他們“過來拿”;不能將“臺階”都鋪設好,而應該讓學生自己搭建階梯;不能只關注課前預設,更需要注重課堂生成,順“思”而為,借“思”而上,因“思”利導,真正促進學生學會學習.

