凸多面體外接球半徑問題的探究*
吳宣良 王先義 (四川省雙流中學 610200)
立體幾何是高中數學學習的重要版塊,是培養和考查學生數學建模、直觀想象和數學運算等數學素養的重要載體.凸多面體外接球半徑問題是立體幾何中的典型問題,也常出現在高考選填壓軸和高聯試題中,這類問題對學生的直觀想象和數學運算素養都有較高的要求.此前,許多研究者對此問題進行分類總結出諸多模型,但其模型種類復雜多樣,學生理解和掌握都較為困難.本文先從已有的凸多面體外接球模型出發,提煉問題模型,尋找通性通法,再通過幾何畫板獲得球體半徑確定的關鍵要素,并根據要素探究凸多面體外接球半徑的統一公式,最后對相關公式進行簡單應用,現整理成文,以饗讀者.
1 凸多面體外接球半徑研究緣由
筆者查閱了近年來研討外接球半徑求法問題的各類文獻,發現大多數文獻以分類討論為主,大體可以分為六種模型[1-4].
墻角模型:其特征是四面體某一頂點處的三條棱兩兩垂直,將四面體補為長方體求得外接球半徑(圖1).

圖1 圖2 圖3
垂面模型:其特征是四面體中存在一條直線垂直于一個平面,根據外接球球心位置及其線面垂直關系求得外接球半徑(圖2).
切瓜模型:其特征是四面體中存在兩個平面互相垂直,且其中一條棱為截面圓的直徑,利用截面圓直徑與外接球球心共面的特征求得外接球半徑(圖3).
折疊模型:其特征是由兩個等腰三角形拼接在一起而成的四面體,利用兩個三角形外接圓圓心確定球心,再利用勾股定理進行求解(圖4).
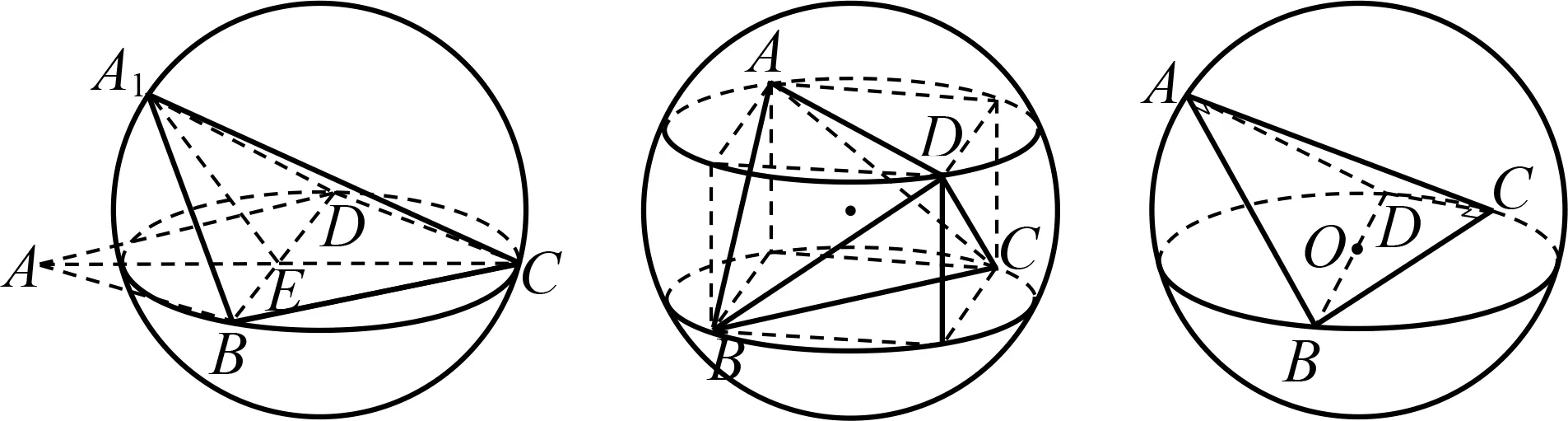
圖4 圖5 圖6
對棱相等模型:其特征是四面體三組對棱長度相等,通過構造長方體模型求解外接球半徑(圖5).
兩直角三角形拼接模型:其特征是由兩個斜邊相等的直角三角形相互拼接得到的四面體,根據幾何特征直接確定球心在兩直角三角斜邊中點處(圖6).
以上六種模型都是解決凸四面體的外接球半徑的常用模型.根據六種模型的特征,大致可以分為三類:第一類是四面體內存在兩個相互垂直的面,即前三種模型;第二類是四面體中有兩個三角形的外接圓半徑相等,即后三種模型.
此時,筆者產生了三個疑問:
問題1 對于任意的凸四面體外接球半徑問題,是否存在通性通法進行求解?
問題2 如果存在通性通法,是否存在完整統一的凸四面體外接球半徑公式呢?
問題3 如果一般的凸多面體存在外接球時,它的外接球半徑又該如何求解呢?
2 凸多面體外接球半徑統一公式
通過作圖分析發現,任意球體的半徑都與它球面上任意兩個不重合的相交截面圓的半徑和截面的二面角有關,這就是解決存在外接球的凸多面體外接球半徑問題的通性通法.
鑒于此,下面通過建模研究凸多面體的外接球半徑、外接球兩個相交截面圓的半徑、外接球兩相交截面圓交線長以及這兩個截面圓所在平面的二面角大小的代數關系,計算得到外接球半徑的統一公式,也即解決上述三個疑問,得到一般的命題如下:
命題設凸多面體外接球的兩個相交截面圓的半徑分別r1,r2(r1≥r2),這兩個截面交線長度為L,兩個截面所在平面構成的二面角大小為θ,則該凸多面體的外接球半徑R可以表示為:
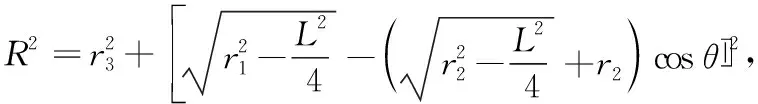
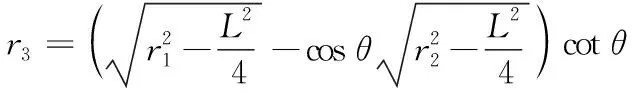
證明如圖7,圓O1與圓O2的半徑分別為r1,r2(r1≥r2),兩圓所在平面構成的二面角的平面角大小為θ,外接球半徑為R.設A,B兩點為圓O1與圓O2的兩個交點,連結AB,則AB=L.作半徑為r3的圓O3,使得圓O3所在的平面垂直于圓O1所在的平面,且圓O2與圓O3同過球上一點Q.設圓O3與圓O1交于C,D兩點,弦AB,CD的中點分別為M1,M2,直線OO1與M1Q的交點為E.
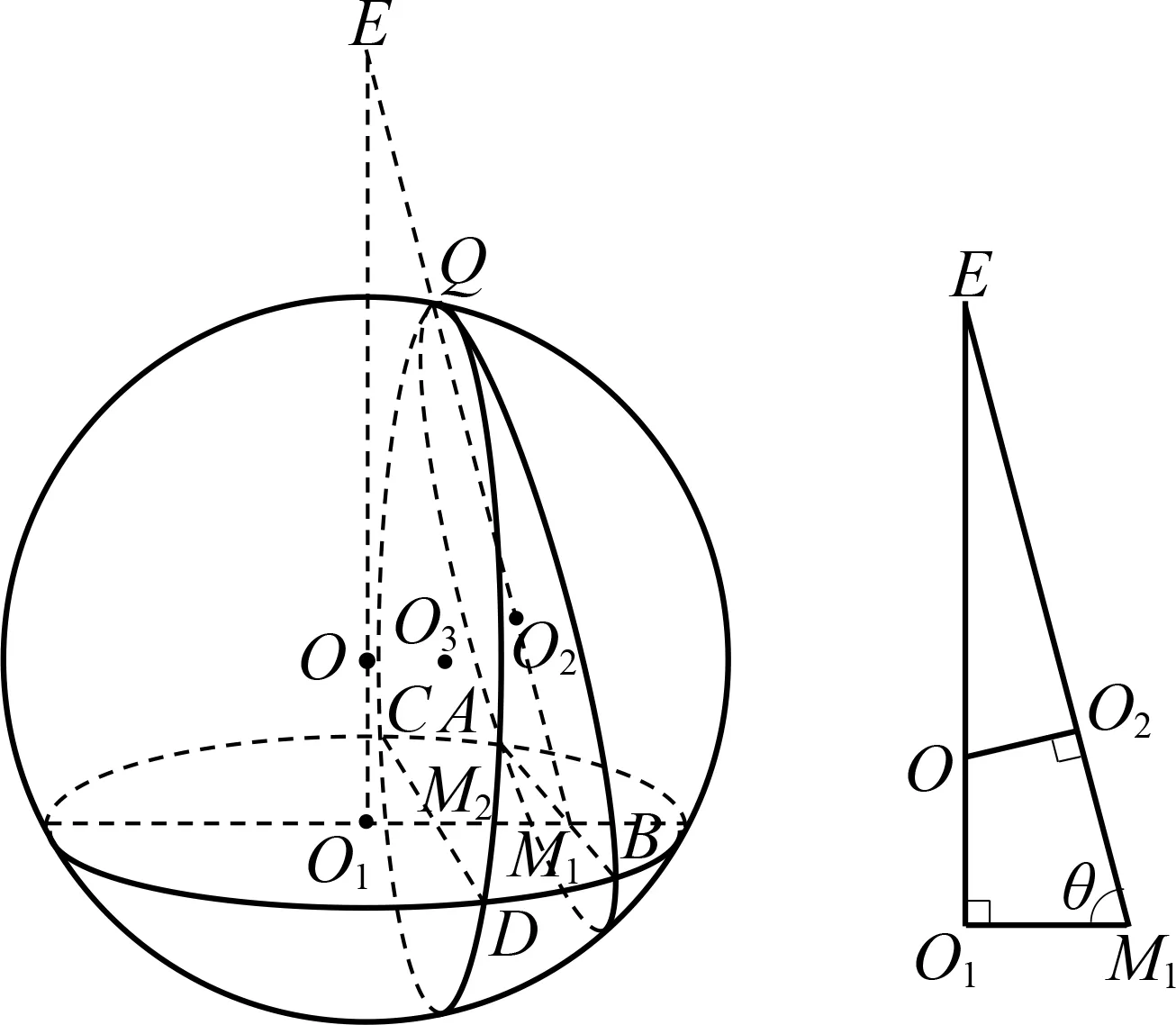
圖7
r3=O3Q=M2Q-O3M2=M2Q-O1O,M2Q=M1Qsinθ=(r2+O2M1)sinθ.
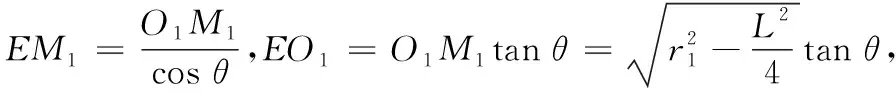



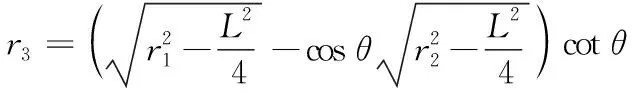
在命題的證明過程中,通過構造與圓O1所在的平面垂直的圓O3,再根據圓O1和圓O3的半徑、公共弦長與其外接球半徑的關系,推導出外接球半徑的統一公式,此公式是求解凸多面體外接球半徑的統一公式.下面將多面體條件特殊化,可得到更為簡潔的多面體外接球半徑公式.
3 兩類特殊的凸多面體外接球半徑公式
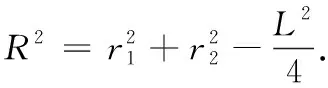
注:此公式即為文首中提到的前三種模型(墻角模型、垂面模型和切瓜模型)的外接球半徑公式.
如果外接球的兩個截面圓的半徑相等時,可以得到如下推論:

注:此公式即為文首中提到的后三種模型(折疊模型、對棱模型和拼接模型)的外接球半徑公式.
4 凸多面體外接球半徑統一公式簡單應用
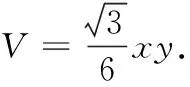
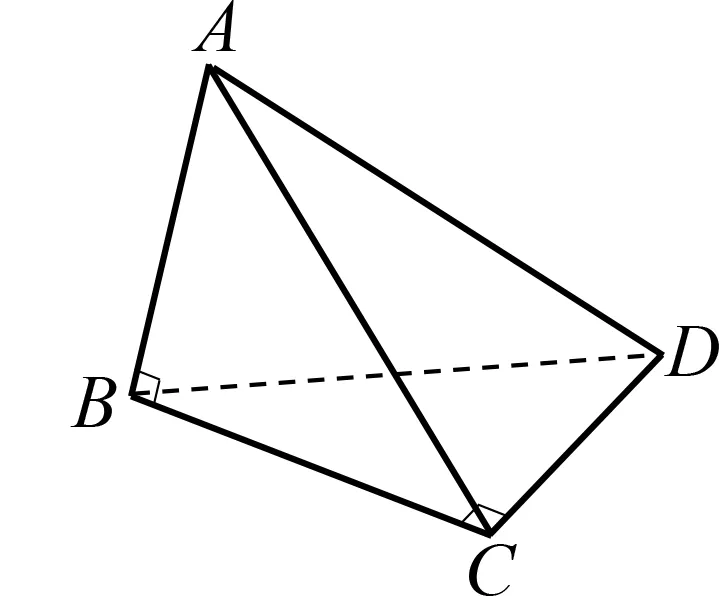
圖8
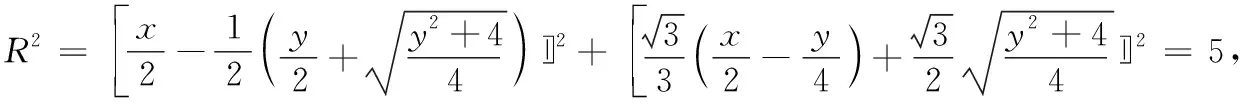
例2(2019陜西高中數學聯賽預賽)如圖9,在棱長為1的正四面體A-BCD中,G為△BCD的重心,M是線段AG的中點,則三棱錐M-BCD的外接球表面積為.
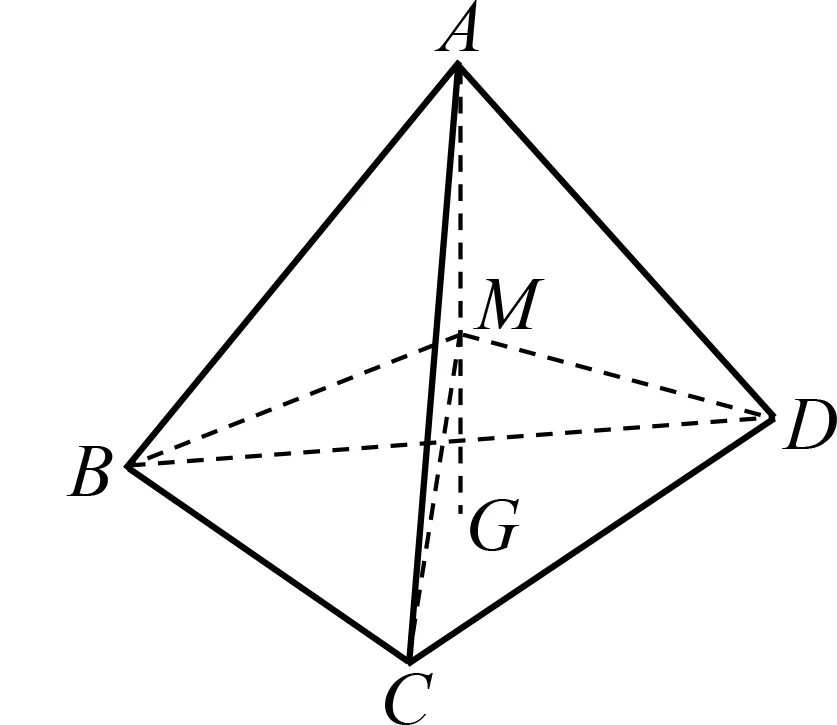
圖9
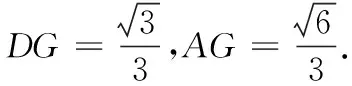
在△MBC中,MC2+MB2=BC2,所以∠BMC=90°.同理可得∠CMD=∠BMD=90°,所以平面BMC⊥平面CMD.
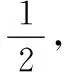
例3(2018山西高中數學聯賽預賽)在四面體A-BCD中,棱BC=3,其余各棱長均為2,則四面體A-BCD外接球半徑為.
解析如圖10,由題意得BC=3,AB=AC=AD=BD=CD=2.
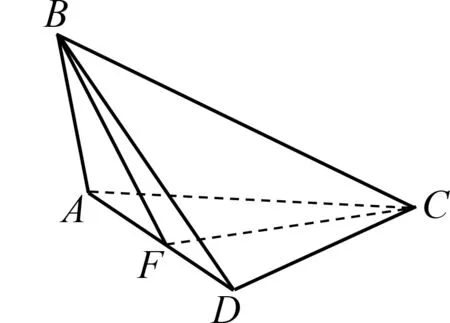
圖10


評注 例1、例2、例3均為高中數學聯賽試題,這三題也可以利用幾何法作出球心,再利用幾何關系計算外接球半徑,但對學生的邏輯推理和直觀想象素養要求較高.此處借助命題及其推論,可以降低作圖和計算難度,節約時間成本,提高思維的經濟效益.
凸多面體外接球半徑問題在高聯和高考中考查得非常廣泛,在2017年甘肅和福建高中數學聯賽中也進行了考查,在高考全國卷和地方卷對凸多面體外接球半徑進行了多次考查,限于篇幅原因,本文不一一列舉作答,有興趣的讀者可以嘗試利用凸多面體外接球半徑統一公式進行求解.
5 結束語
“通性通法”中,“通性”是概念所反映的數學基本性質,“通法”是概念所蘊含的思想方法.章建躍博士認為,在解題教學中要使學生逐步養成從基本概念、基本原理及其聯系性出發思考和解決問題的習慣,要注重大巧若拙的通性通法,而不是將學生的注意吸引到技巧上[5].本文探究了一種求解多面體外接球半徑的一般思路,力求“做一題,會一類,通一片”.在解題和教學的過程中,要避免就題論題,要有從特殊到一般的探索意識,歸納和總結問題的共性和特點,從而獲得問題的通法,提升能力并優化認知結構.

