基于粒子群算法的高溫高壓三軸試驗機控制系統優化

林 峰，孟巧榮，b，李亞軍，陳 濤，李 明

(太原理工大學 a.礦業工程學院，b.原位改性采礦教育部重點實驗室，太原 030024)

巖石力學的發展始終伴隨著試驗機的發展而逐漸發展、成長和成熟[1]。然而在巖體高溫高壓實驗過程中，隨著溫度的升高，巖體會發生物理化學變化，影響巖體的實際承壓狀況，另外，傳熱傳質也會使巖體溫度發生波動。因此，巖體高溫高壓實驗過程中，壓力和溫度隨時間的波動較大，對試驗機的溫度和壓力需要實時控制。試驗機控制系統的升級優化是必不可少的。巖石力學特性的不同，三軸加載液壓伺服系統對巖石壓力的影響而不同。每次試驗的巖石具有不同的負載質量和負載剛度，液壓系統的穩定性隨力學特性的不同而變化。三軸高溫高壓試驗系統是在實驗室環境里模擬巖石深部環境，再現深部巖體的軸壓、圍壓、地下水動力(水壓滲流)和地熱溫度的物理條件，對巖石的綜合物理力學性能進行研究而設計的一種機械系統[2]。電阻加熱爐主要是利用電流通過熱電阻絲或導電介質產生焦耳熱能，根據電阻加熱爐的加熱對象的不同，在工業生產過程中又可以分為直接加熱和間接加熱兩種形式[3]。由于間接加熱不要求被加熱物體為導體，故其適用范圍相對較廣[4]。目前大多數對液壓與溫度系統的控制一般使用傳統PID控制器進行調節。傳統PID控制器對于具有非線性、強干擾、不確定性特點的系統難以達到理想的控制效果[5-7]。PID的參數決定了PID控制器的控制效果。一般的 PID 參數整定方法過程較為復雜，在工作現場中常規方法往往因整定困難得不到非常有效的PID參數[8-10]。因此，PID參數整定問題愈發受到專家學者的重視。常規PID參數整定方法有ZN(Ziegler-Nicholes)[11-13]、CC(Cohen-Coon)方法[14]、內部模型控制(internal model control，IMC)[15-17].盧彬彬等[18]應用人工蜂群(ABC)算法實現了對航空發動機PID控制器的優化；顧冬華等[19]應用模糊神經網絡控制方法，與無菌包裝預熱系統的PID控制器結合，實現了對PID參數的有效整定；宋娟[20]應用混合果蠅算法實現了對PID參數的尋優設計；譚冠政等[21]應用蟻群算法對智能人工腿PID控制器進行了優化設計。馬麗楠等[22]提出IMC-PID控制器，建立濾波器參數與PID控制器參數之間的關系，解決了由于雙閉環獨立PID整定參數多且復雜的問題。隨著具有非線性行為、高階和長響應時間的工業系統復雜性的提升，進一步增加了PID參數設置的困難[23]。

呂紅芳等[24]應用了基于免疫粒子群算法對PID參數進行優化，并證明了該算法的有效性；孫言鍇等[25]應用了粒子群算法與模糊算法相結合的方法對PID參數進行了優化，解決了前驅體材料生產中反應釜中pH值控制。

粒子群算法對問題的維數相對敏感，將粒子群算法與其他算法相結合會因維數的增加而增加運算復雜度。本文為了確保試驗機控制系統的穩定性提出了基于粒子群算法的PID參數優化方法。該方法相較于其他PID參數控制策略具有算法簡單、搜索速度快、效率高等特點，使得試驗機在試驗過程中對外界環境及其巖石內部變化造成的干擾做出及時反應，并且迅速達到試驗條件設定值后趨于穩定狀態。

1 高溫高壓三軸試驗機及控制系統數學模型

圖1所示為高溫高壓三軸試驗機。試驗機由系統控制平臺、高溫三軸應力室、加熱系統組成[26]。為了研究粒子群算法優化PID控制器對試驗機控制系統的有效性，需要對試驗機控制系統建立數學模型，得出試驗機控制系統傳遞函數。文中對試驗機控制系統均采用機理建模法。

圖1 高溫高壓三軸試驗機

1.1 液壓控制系統及數學模型

高溫高壓三軸試驗機液壓控制系統圖如圖2所示，由油箱、液壓泵、濾油器、電液伺服換向閥、電機、溢流閥、復合液壓缸、壓力傳感器、控制器和伺服放大器等組成。

1-油箱；2-濾油器；3-電機；4-液壓泵；5，9-電液伺服換向閥；6-溢流閥

假定閥和液壓缸的連接管道對稱且短粗，管道動態與管中壓力損失可以忽略；液壓缸各工作腔內各處壓力相等，油溫、體積彈性模量是常數；液壓缸內、外泄漏均為層流流動[27]，可以得出：

電液伺服閥流量方程：

QL=kqxv-kcpL.

(1)

式中：QL為液壓缸進油輸入流量，m3/s；kq為伺服閥流量增益，L/(min·m)；xv為閥芯位移，m；kc為伺服閥的閥門壓力，MPa；pL為供油壓力，MPa.

液壓缸流量方程：

(2)

式中：Ap為液壓缸活塞有效工作面積，cm2；s為拉普拉斯變量；xp為液壓缸活塞位移，m；Cip為液壓缸總的泄露系數，L/(min·MPa)；Vt為系統總壓縮體積系數；βe為液壓油彈性模量，MPa.

液壓缸力平衡方程：

Fg=Mts2xp+Bpsxp+Ksxp+FL.

(3)

式中：Mt為液壓缸負載質量，kg；Bp為液壓缸負載阻尼系數，(N·S)/mm；Ks為液壓缸負載彈性剛度，N/m；FL為液壓缸所受外干擾力，N.

綜上(1)-(3)式可得出電液伺服閥控液壓缸的傳遞函數Gp(s)：

(4)

假設液壓系統無彈性負載，負載僅為慣性負載，負載彈性剛度為0，負載阻尼系數Bp以及總流量壓力系數kce很小，故忽略不計，且液壓缸所受外干擾力與負載質量的作用相對比相差的數量級較大，對液壓系統影響不大故忽略不計。因此(4)式可化簡為：

(5)

電液伺服閥傳遞函數：

在動態特性分析中，電液伺服閥為二階振蕩環節。

(6)

式中：ωSV為電液伺服閥固有頻率，Hz；KSV為電液伺服閥流量增益，L/(min·m)；ζSV為電液伺服閥阻尼比。

伺服放大器傳遞函數：

(7)

式中：I(s)為輸出電流，A；U(s)為輸入電壓，V.

壓力傳感器傳遞函數：

(8)

式中：U(s)為輸出電壓，V；Fg2為液壓缸的輸出壓力，N.

由(5)-(8)式可以得到高溫高壓三軸試驗機的液壓系統閉環傳遞函數框圖見圖3.

圖3 液壓系統閉環傳遞函數框圖

1.2 溫度控制系統及數學模型

通過分析電阻加熱內部機理，得知其是一維的關系結構表達式。高溫高壓三軸試驗機溫控系統圖如圖4所示。

圖4 高溫高壓三軸試驗機溫度控制系統

電阻加熱內部溫度與熱量方程：

(9)

式中：Q為電阻絲加熱的總熱量，J；G為加熱爐內控制重量，kg；Ca為空氣的比熱容；C為熱容。

熱能增量形式方程：

(10)

式中：R為熱阻，Ω；ΔQ為熱量增量，J；ΔTI為加熱爐內的溫度變化，℃；ΔTO為加熱爐外的溫度變化，℃.

對(10)式進行拉普拉斯變換得到：

(RCs+1)Tr(s)=RQ(s).

(11)

由式(9)-(11)得出電阻絲加熱系統傳遞函數：

(12)

式中：K為放大系數，K=R；T為慣性時間常數，T=RC.

對試件進行加熱時，電阻絲加熱爐的溫度不是循序漸進地增加，熱傳遞過程有一個從輸出到響應的延遲，存在一個漸變量。延遲的時間長短與加熱的容積有關。因此，考慮到外部環境的干擾，電阻絲加熱系統傳遞函數可改寫為：

(13)

式中：τ為延遲時間常數。

溫度傳感器熱電偶的傳遞函數：

(14)

由式(13)、(14)可以得出高溫高壓三軸試驗機溫度控制系統閉環傳遞函數框圖見圖5.

圖5 溫控系統閉環傳遞函數框圖

2 粒子群算法優化PID

2.1 粒子群算法概述

粒子群優化算法是一種基于群體智能理論的算法，由Kennedy和Eberhart于1955年提出，源于鳥群捕食的行為，通過種群粒子間的合作與競爭產生群體智能優化搜索[28]。

通俗地講，我們可以把粒子群想象為一群具有相互通訊的正在覓食的鳥群，然而每只鳥不清楚食物所在的具體位置，但是對于鳥類可以通過嗅覺判斷食物與自己的距離以及判斷自己在區域內的位置。鳥群中任意兩只鳥可以清楚對方離食物的距離以及對方的位置。在此假設，每一只鳥飛行都會有慣性，并且每只鳥都會判斷本身距離食物的距離和其它同類距離食物的距離以及它們的位置，然后選擇下一次飛行的方向。最后，鳥群通過相互通訊，匯聚在食物的地點。食物的位置也就是我們在工業應用中產生的最優解。

為了求得最優解(鳥群向食物飛行)，粒子群算法(PSO)提出速度，以此來對粒子群更新，速度反映出鳥兒當前所在的位置距離事物的方向和位移，并且決定鳥兒飛行的方向及位移。速度值是通過個體極值以及全局極值來確定，個體極值就是單個粒子尋找到的最優解，全局極值就是粒子群尋找到的最優解，對應鳥兒自身的飛行目標和同伴的飛行目標，憑借這兩點，鳥兒找到食物所在的位置及粒子群找到最優解。

vt+1=wvt+c1r1(Pt-xt)+c2r2(Gt-xt) .

(15)

xt+1=xt+vt+1.

(16)

式中：v表示粒子速度；x表示粒子的位置；w為慣性權重；c1、c2為加速度常數；r1、r2為[0,1]之間的隨機數；Pt是粒子當前尋找的最優位置；Gt是整個粒子群當前尋找的最優位置。

2.2 PID控制器

目前，工業上使用的控制器大多采用PID控制器，根據輸出值與給定值的差e(t)通過下列數學公式計算來控制輸出。

(17)

式中：Kp為比例系數；Ki為積分系數；Kd為微分系數。

PID控制器的靈敏度也是由這3個參數來確定的，但對于這3個參數通過人為的確定效果并不是很好，并沒有達到控制系統快速響應、穩定運行的狀態。

2.3 粒子群算法優化PID參數

利用粒子群算法(PSO)分別對溫度控制系統PID控制器的參數Kp、Ki、Kd，液壓(軸壓)控制系統PID控制器的參數Kp、Ki、Kd和液壓(圍壓)控制系統PID控制器的參數Kp、Ki、Kd，進行整定。選擇PID控制器中的Kp、Ki、Kd作為粒子群算法(PSO)的粒子，最終的參數優化目標是粒子速度趨于零。粒子群算法(PSO)優化PID參數的流程圖，如圖6.

圖6 粒子群算法(PSO)優化PID參數流程圖

粒子群算法優化PID參數過程：

1) 初始化。粒子群算法(PSO)中的參數，最大迭代次數100次，粒子群規模為100，c1、c2加速度常數為2，慣性權重w=4以及粒子空間搜索范圍。

2) 粒子群隨機產生每一個粒子的速度和位置，通過適應度函數J計算每一個粒子的適應值，確定Pt和Gt.適應度函數J如下：

(18)

3) 通過公式(15)和(16)更新粒子的速度與位置，計算新粒子的適應度，更新粒子最優的Pt和Gt.如果粒子達到預設的迭代次數和適應度下限值，則得出參數最優解結束算法，反之返回步驟2).

2.4 基于粒子群算法的高溫高壓三軸試驗機控制系統PID控制器結構

試驗機控制系統進行軸壓控制時，首先將軸壓信號輸入到PID控制算法中，得到軸壓控制輸出，計算軸壓的控制誤差，粒子群算法通過軸壓控制誤差反饋對PID控制參數進行調整，使軸壓控制誤差盡可能減小，提高軸壓的控制精度，控制結構圖如圖7所示。

圖7 軸壓控制系統結構圖

圍壓控制原理如圖8所示。首先將圍壓信號輸入到PID控制算法中，得到圍壓控制輸出，計算圍壓的控制誤差，粒子群算法通過圍壓控制誤差反饋對PID控制參數進行調整，使圍壓控制誤差盡可能減小，提高圍壓的控制精度。

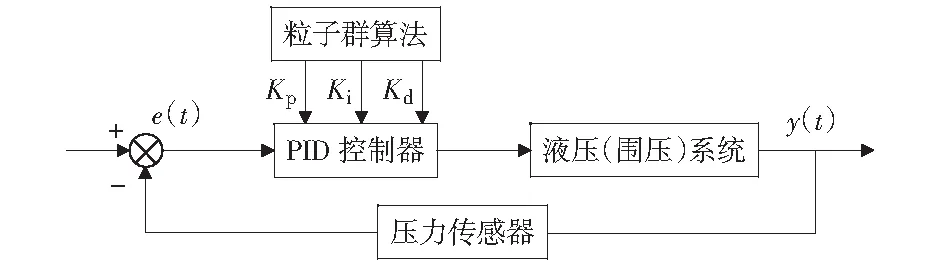
圖8 圍壓控制系統結構圖

溫度控制原理如圖9所示。首先將溫度信號輸入到PID控制算法中，得到溫度控制輸出，計算溫度的控制誤差，粒子群算法通過溫度控制誤差反饋對PID控制參數進行調整，使溫度控制誤差盡可能減小，提高溫度的控制精度。

圖9 溫控系統結構圖

3 仿真實驗分析

液壓系統在Simulink仿真過程中的參數：液壓油彈性模量Ee=700 MPa；液壓缸負載阻尼系數Bp=9 (N·S)/mm；液壓缸活塞有效工作面積(軸壓)Ap=0.20 dm2；液壓缸活塞有效工作面積(圍壓)Ap=0.59 dm2；液壓缸總的泄露系數Cip=1.3 L/(min·MPa)；伺服閥的閥門壓力kc=14 MPa；伺服閥流量增益kq=2 L/(min·m)；液壓缸負載質量Mt=20 kg；系統總壓縮體積系數Vt=7.16 dm3.溫控系統在Simulink仿真過程中的參數：K=8；T=3 360；τ=60.

分別利用傳統PID控制器和模糊PID控制器，粒子群算法優化PID控制器對試驗機的溫度壓力進行控制，通過仿真研究得到系統的階躍響應見圖10、圖11和圖12.

圖10 溫度控制系統階躍響應

圖11 液壓(圍壓)控制系統階躍響應

圖12 液壓(軸壓)控制系統階躍響應

由圖10可知，粒子群算法優化PID控制器超調量要比模糊PID控制器縮小約0.1，比傳統PID控制器縮小約0.2.粒子群算法優化下的PID控制器穩態響應時間比模糊PID控制器縮短約10 s，比傳統PID縮短約22 s.系統的穩定性和動態性均得到了很大的改善。

由圖11可知，粒子群算法優化PID控制器超調量要比模糊PID控制器縮小約0.125，比傳統PID控制器縮小約0.275.粒子群算法優化下的PID控制器穩態響應時間比模糊PID控制器縮短約2 s，比傳統PID縮短約8 s.

由圖12可知，粒子群算法優化PID控制器超調量要比模糊PID控制器縮小約0.075，比傳統PID控制器縮小約0.235.粒子群算法優化下的PID控制器穩態響應時間比模糊PID控制器縮短約6 s，比傳統PID縮短約18 s.

4 結論

本文通過分析試驗機控制系統的工作原理與控制機理，提出基于粒子群算法的PID控制器對試驗機的溫度壓力進行實時控制，通過仿真實驗驗證，結論如下：

1) 對于具有大滯后大延遲的電阻加熱溫控系統，經過粒子群算法整定后的PID控制器相較于模糊PID超調量縮小約8%，穩態響應時間加快約11%，相較于傳統PID超調量縮小約16%，穩態響應時間加快約20%.

2) 對于液壓(圍壓、軸壓)系統經過粒子群算法整定后的PID控制器相較于模糊PID超調量分別縮小約10%和6%，穩態響應時間加快約50%和75%。相較于傳統PID超調量分別縮小約21%和18%，穩態響應時間加快約75%和90%.

因此，基于粒子群算法的PID控制器可以大大提高試驗機的穩定性和動態響應性能，提高試驗機對環境和巖樣加熱加壓的擾動控制。