融合混沌對立和分組學習的海洋捕食者算法

馬 馳，曾國輝，黃 勃，劉 瑾

上海工程技術大學 電子電氣工程學院，上海 201600

隨著人工智能技術的發展，優化求解問題越來越復雜，導致了相當大的計算成本。傳統的牛頓法、梯度下降法等局部搜索方法效率低下，容易陷入局部最優，已不能滿足實際需求[1-2]。元啟發式群智能優化算法的核心思想主要源于動物行為或者物理現象，其核心環節是探索和開發，探索用于在解空間中尋找新的解，以獲得全局最優值并避免陷入局部收斂。該算法根據全局最優值進行局部搜索，得到最優解，其簡單易行，對初始值不敏感，運行時間短，近年來得到了廣泛重視[3-4]。群智能算法能夠有效解決人工智能領域中許多復雜且具有挑戰性的優化問題，主要應用于組合優化、特征選擇、圖像處理、生產制造與調度[5]等領域。近年來提出的元啟發式算法包括粒子群算法（particle swarm optimization，PSO）、灰狼優化算法（gray wolf optimization，GWO）、飛蛾撲火算法（moth flame optimization，MFO）、鯨魚優化算法（whale optimization algorithm，WOA）、蝴蝶優化算法（butterfly optimization algorithm，BOA）、海洋捕食者算法（marine predator algorithm，MPA）、多元宇宙優化算法（multi-verse optimizer，MVO）、原子搜索算法（atom search optimization，ASO）等。

MPA算法是2020年由Faramarzi等提出的模擬海洋捕獵行為的元啟發式算法，該算法的靈感來自于海洋捕食者和獵物的運動方式。其尋優過程分為三個階段，捕食者和獵物在這三個階段中按照萊維運動或者布朗運動進行位置更新[6]。同時，獵物在被捕食的同時也充當捕食者身份，使得算法更具有動態特性。且MPA算法獨有的海洋記憶存儲階段與海洋漩渦影響階段，可以進一步提高更新后的種群質量，相對粒子群、差分進化等經典算法以及上述多數算法，具有更快的收斂速度和收斂精度。

雖然基本MPA算法在優化問題方面具有顯著的優勢，但是仍然存在著群智能算法容易陷入局部最優、收斂速度較慢的問題，仍需進行改進以提高其優化性能。Elaziz等人提出了一種混合MPA和MFO的MPAMFO算法[7]，用MFO代替了MPA的局部搜索方法，提高了MPA的開發能力，但是收斂速度仍有待提高。Abdel等人提出了一種改進的MPA（improved marine predator algorithm，IMPA）[8]。該算法引入了基于排序的多樣性減少策略，以最佳個體位置直接替換適應度持續不良的搜索個體的位置，提高了MPA的性能并加快了收斂，但是種群多樣性的減少，可能進一步增加陷入局部最優的風險，使算法的可靠性降低。Fan等人提出了基于新的位置更新規則、慣性權重系數和非線性步長控制參數策略的改進MPA（modified MPA，MMPA）[9]。MMPA表現出優越的性能，在精度、收斂速度和穩定性方面得到了有效的提升，但是改進的位置更新規則在捕食者和獵物的每個運動階段均需按照概率分成兩段，分段匹配正余弦函數，規則過于繁瑣。Elaziz等人提出了一種增強型MPA（enhanced marine predator algorithm，MPA）[10]，將差分進化算子（DE）引入MPA算法中，利用差分進化算子加強MPA的探索階段，以便于高效地發現搜索空間，降低陷入局部最優的概率，算法結構簡單，但是通過文中實驗測試對比可知，該EMPA算法對尋優精度的提升十分有限。

為了更好地提升MPA算法尋優精度和收斂速度，本文將混沌對立初始化與分組維度學習策略結合，同時引入t分布變異算子，提出了一種多策略改進的MPA算法（improved MPA for multi-strategy，MSIMPA），使算法同時獲得了尋優精度和收斂速度上的顯著提升。

1 海洋捕食者算法

海洋捕食者算法（MPA）是一種模擬海洋獵物和捕食者在自然界中生物行為的元啟發式算法。獵物位置初始化在解決空間上均勻分布，適應度最佳的作為頂級捕食者用于構造精英矩陣，矩陣定義為：其中，每一行均為頂級捕食者的位置向量，n是種群數量，d是個體維度值。捕食者和獵物均被認為是搜索個體，因為每一個個體在捕食的時候，也同樣面臨著被捕食的可能。在每次迭代結束時，如果頂級捕食者被更好的捕食者取代，精英將被更新。

另一個是獵物矩陣，捕食者基于這個矩陣更新它們的位置。因此，初始化創建了最初的獵物，其中最合適的一個獵物（捕食者）構建了精英。獵物矩陣如式（2）所示。

MPA通過三個階段模擬海洋捕食者及其獵物的生活，總結如下：

階段1獵物比捕食者移動得快或在高速比時(v≥10)。這個階段發生于迭代初期。捕食者的最佳策略是根本不移動，該階段數學模型表述如下：

其中，RB表示布朗運動隨機向量，P是等于0.5的常數，R表示[0，1]之間的隨機均勻分布值。Iter表示當前迭代次數，MaxIter描述最大迭代數，RB與獵物的點乘模擬了獵物的運動。

階段2獵物和捕食者以相接近的速度或單位速度比移動(v=1)。該策略發生在迭代中期，種群被分為兩部分，一部分被指定用于探索，另一部分用于開發。這時，捕食者做布朗運動，獵物做萊維運動。該階段數學模型表述如下：

其中，RL表示萊維運動隨機向量，CF表示控制捕食者移動步長的自適應參數。

階段3捕食者比獵物移動得快或在低速比時(v=0.1)。該階段發生在迭代時期，該階段主要與局部高開發能力相關，此時捕食者的最佳策略為萊維運動，該階段數學模型表述如下：

其中，RL與精英矩陣的點乘模擬了捕食者的萊維運動，并通過增加精英的步長，將捕食者的運動模擬為獵物位置的更新。

除了上述階段之外，渦流的形成和魚類聚集裝置（fish aggregating devices，FADs）對捕食者也有影響，該階段數學模型表述如下：

其中，pf=0.2表示優化過程中受FADs影響的概率，U是通過在[0，1]中生成一個隨機向量來構造的，表示包含0和1的二進制向量數組。如果數組小于0.2，則將數組更改為0，如果大于0.2，則更改為1。r是[0，1]中的均勻隨機數，r1和r2下標表示獵物矩陣的隨機索引。MPA算法具有海洋記憶功能，其本質類似于貪婪策略，在算法迭代開始和位置更新結束都需要進行適應度對比，將更好的解替換先前的解。

2 改進海洋捕食者算法MSIMPA

2.1 加入混沌對立學習策略

2.1.1 Tent混沌映射

混沌映射是一種非線性理論，具有非線性、普適性、遍歷性和隨機性的特點，可以按自身的特性在一定范圍內不重復地遍歷所有狀態，在智能算法優化中能幫助生成新的解，增加種群多樣性，因而被廣泛應用[11]。Tent映射迭代速度快，混沌序列在[0，1]之間均勻分布，其表達式如下：

其中，λt是第t次迭代時產生的混沌數，T是最大迭代次數，α是介于[0，1]的常數，本文選取α=0.7。

圖1為Tent映射迭代500次，劃分20個區間時的序列分布直方圖。由圖1可以看出，Tent映射在0～1之間均勻分布。

2.1.2 對立學習

在解決問題的時候，考慮到無效解決方案的對立側可能存在更好的解決方案，Tizhoosh提出了對立學習策略（opposition-based learning，OBL）[12]。近年來OBL已經有效地應用于各種群智能算法中。在群智能算法初始化種群的過程中，隨機生成的部分個體往往會分布在遠離最優解的無效區域和邊緣區域，進而降低了種群的搜索效率。采用OBL策略，在種群初始化中引入一個隨機解及其對立解要比引入兩個獨立的隨機解更能提高初始種群的質量。假設某個d維個體位置為：

設其個體位置的下界和上界分別為lb、ub，則其對立側位置可以表示為：

但是，在目標函數上下界限對稱的時候，由式（16）可看出，所生成的反向解為原來解的完全鏡像（取負），對部分具有偶函數特性的函數，完全鏡像解與原解目標值一致，不適合將兩個種群做適應度排序，無法有效獲得高質量種群。

2.1.3 混沌對立策略

本文將Tent混沌映射與OBL相結合，提出了一種新的TOBL（Tent and opposition-based learning）機制。TOBL的數學模型如下：

其中，為第i個獵物對立位置的第j維分量。

TOBL策略相當于以目標函數上下界限的和為中心，利用Tent的均勻變化，來動態壓縮原初始種群的分布范圍，并在壓縮的同時盡量讓種群均勻。

圖2為不同策略下30個個體在[-20,20]的二維平面初始化分布圖，由圖2（a）、（b）可以看出，兩種方式的初始化分布呈現完全的中心對稱，這種鏡像現象會制約對立解的有效性。圖2（c）的TOBL初始化分布雖然不如圖2（a）中的個體分布均勻，但是兩種方式的初始化分布差異很大，更適合將兩者合并，然后按照適應度將個體排序，擇優選取與原來相同數量的個體，作為新的初始化種群，進而提高初始化種群的質量。

假設海洋捕食者（獵物）種群數量為n，該策略的具體步驟為：首先通過隨機分布生成n個位置，再通過TOBL生成n個混沌對立位置，這些對立位置很有可能更加接近于目標獵物，最后將這2n個位置按照適應度排序，取適應度最佳的前n個獵物位置，作為初始化種群。

2.2 加入自適應t分布

t分布又稱為學生分布[13]，它的分布函數曲線形狀與其自由度n密切相關。

圖3為自由度為5的t分布、標準正態分布和標準柯西分布的函數分布圖像對比。由圖3可知，t分布大致介于標準正態分布和標準柯西分布之間，其自由度n越小，曲線的雙尾就翹得越高，中間峰值越小，整體越加平滑。當n=1時，t分布變為標準柯西分布。反之，自由度n越大，中間峰值越大，整體越加陡峭。當n趨于無窮時，t分布變為標準正態分布。

基本MPA中，獵物更新完位置以后，需要檢測和更新頂級捕食者的位置，并進行一次海洋記憶存儲，接下來再考慮FADs的影響，對獵物的位置做進一步更新。

為了保證此次記憶存儲更加有效，引入自適應t分布算子，在模擬FADs的影響之前，對獵物的位置進行變異，如果變異后的位置更佳，則代替原來的位置。數學模型如下：

其中，Xi′為第i個獵物變異后的位置，t(Iter)為以當前迭代次數為自由度的t分布。在迭代初期，迭代次數較少，t分布近似于柯西分布，分布得更加平滑。此時，t分布算子在大概率上取到較大值，位置變異所采取的步長較大，算法具有良好的全局探索能力，與MPA第一階段的全局搜索特性形成正反饋；在迭代中期，一半的捕食者用于全局探索，另一半的捕食者用于局部開發，而此時t分布介于柯西分布和正態分布之間，t分布算子在大概率上取值相對折中，同時兼顧了MPA第二階段的全局搜索和局部開發，使捕食者更容易返回到獵物豐富的地區并成功覓食，進而對算法性能形成正反饋；在迭代后期，t分布近似于標準正態分布，分布得更加集中，t分布算子在大概率上取較小值，致變異所采取的步長較小，兼顧了MPA第三階段的局部開發特性。

2.3 加入分組維度學習策略

在算法迭代過程中，有些獵物位置的某些維度實際上可能早已達到了最優維度，由于其中個別維度的影響，使得這些獵物位置的適應度變差[14]。為了能在海洋里生存下去，位置差的獵物（捕食者）需要向位置好的獵物（捕食者）學習捕食本領，基于這個思想，提出了一種分組維度學習的策略。將FADs影響后的獵物按照適應度排序平均分成兩組，適應度好的一組稱為精英組，適應度差的一組稱為學習組[15]。

2.3.1 學習組維度交叉策略

因為精英組的維度各有優劣，所以將精英組的位置維度取平均值，學習組的每一個獵物都向精英組平均維度進行學習。該策略將學習組每個獵物的每一維度同精英組平均維度值做差，按照絕對差異大的優先交叉原則，取絕對差異大的前H1個對應維度逐一交叉，如果交叉后獵物的適應度更好，則交叉對應維度，反之則不交叉。該策略的數學模型為：

其中，XL,i表示學習組第i個獵物位置，Xk,crossL,i表示與精英組平均維度值第k維交叉后的第i個獵物位置，ΔXkL,i表示學習組第i個獵物第k維和精英組平均維度第k維的絕對差異，XkJAVG表示精英組平均值的第k維。圖4為H1=2時學習組維度交叉示意圖。

以圖4學習組第2個個體為例，其第1維交叉以后適應度更好，交叉成功。第3維交叉后適應度變差，故交叉失敗。當H1取值越大，所交叉的維度就越多，對學習組個體而言，會使得學習組的個體大程度上接近精英組平均值，減小了學習組個體之間的差異。此時，雖然種群平均適應度減小，加快了收斂速度，但是個體差異性的減少會帶來陷入局部最優的風險，即使收斂精度相比原算法有提升，但仍有一定概率使改進算法尋優精度降低。當H1取值越小，交叉次數越少，相比于未交叉之前的個體差異微小。雖然個體多樣性得到保持，但是較少維度的交叉大大減弱了改進算法跳出局部最優的能力，同樣有陷入局部最優的風險。而且交叉過少，個體之間得不到很好的學習，會降低收斂速度，因此，H1的選取要折中考慮。經過大量仿真測試，選取個體維度一半左右進行交叉效率最高，本文實驗中，選取H1等于個體維度數的一半。

學習組向精英組平均值進行維度學習的過程中，質量較差的學習組個體就不至于跨越太大的步長，以免越過全局最優點及其鄰域。因此，學習組的平均維度學習會大大減少該部分個體向最優值迭代的次數，提升了收斂速度。

2.3.2 精英組維度交叉策略

精英組整體離全局最優點相對較近，因此不適合全部維度的擾動變異，這樣會導致精英在最優解附近徘徊，影響收斂精度。令精英組的獵物相互之間取長補短，在保留自己優勢維度的前提下，向相鄰的獵物進行學習。該策略交叉原則和學習組獵物交叉原則相同，只是將交叉對象，由精英組平均維度值更換為與該獵物相鄰的前一個獵物。設精英組每個獵物取絕對差異大的前H2個相鄰對應維度逐一交叉，圖5為H2=4時精英組維度交叉示意圖。

以圖5精英組第3個個體為例，其第1、5維和倒數第2維交叉以后適應度更好，交叉成功。第7維交叉后適應度變差，故交叉失敗。有關H2的選取規則，同理于H1的選取規則。本文實驗中，選取H2等于個體維度數的一半。

該策略相當于原來質量較高的個體，僅朝著所交叉的維度方向步進，仍保留其他優勢維度。相比于整個個體的變異，這種策略的擇優性更強，可以有效增強算法維度的縱深挖掘性能，提高原算法的收斂精度。

2.4 MSIMPA算法實現步驟

步驟1由式（14）～（17）對獵物的位置進行混沌對立初始化，并設置種群規模、最大迭代次數、FADs等相關參數。

步驟2計算每個獵物適應度值，并將適應度值進行比較、替換，由最佳獵物構成頂級捕食者矩陣，并進行海洋記憶存儲。

步驟3由式（3）～（11）更新獵物位置和移動步長。

步驟4由式（18）的t分布變異算子進行位置擾動更新，并保留最佳位置。

步驟5重新計算每個獵物適應度值，并將適應度值進行比較、替換，由最佳獵物構成頂級捕食者矩陣，并進行海洋記憶存儲。

步驟6考慮FADs和漩渦的影響，由式（12）進一步更新位置，并保留最佳位置。

步驟7將更新后的種群按照適應度優劣均分成學習組和精英組，由式（19）～（20）進行維度交叉，交叉后適應度變好則交叉對應維度，反之則不交叉。

步驟8判斷算法是否滿足迭代條件，若滿足，則算法終止，否則轉至步驟2。

2.5 MSIMPA復雜度分析

算法的復雜度主要取決于算法語句的重復執行次數，MPA中循環次數主要受最大迭代次數T、種群規模N和個體維度D的影響[16]。根據上節步驟分析MISMAP：步驟1混沌對立初始化種群數量翻倍，增加O(N×D)運算量，但復雜度仍為O(N×D)；步驟2和步驟5搜尋頂級捕食者以及海洋記憶存儲的復雜度為O(N×T)；步驟3位置更新復雜度為O(N×D×T)；步驟4對每個個體位置擾動，復雜度為O(N×T)；步驟6對整體位置統一增加一個步長，復雜度為O(T)；步驟7對每個個體的一半維度進行維度學習，復雜度為O(N×D×T)。綜上，略去低次項，原算法復雜度為O(N×D×T)，MSIMPA復雜度增加體現在步驟1、步驟4和步驟7，運算量雖然稍有增加，但是總體復雜度不變，不影響算法執行效率。

2.6 MSIMPA收斂性分析

原始海洋捕食者算法按照迭代次數分為三個尋優階段。階段2為階段1和階段3的整合，其局部開發遵循階段1的收斂性，全局搜索階段遵循階段3的收斂性，故無需對其單獨分析。文獻[17]中，算法的提出者已經詳細證明了階段1和階段3的收斂性，下面僅給出結論。在階段1，原算法收斂性取決于φ1：

由上式可知，當φ1＜1時，MPA在階段1收斂，否則發散。而階段1原本就是用來全局搜索，因此它按概率發散也無關緊要。

在階段3，MPA收斂，且收斂于頂級捕食者構成的精英矩陣E，即全局最優位置：

綜上，MPA在整個迭代過程中，最終是呈現出收斂的。在MSIMPA中，主要加入了三個策略。其中，混沌對立策略僅參與一次初始化種群，不參與算法的迭代過程，不對算法收斂性造成影響，無需單獨分析。自適應t分布以及分組學習，本質上都是引入隨機變異，來對原來的種群進行擾動，然后遵循貪心策略保留精英。

根據數列基本定理，有：

定理1單調不升且存在下界的數列{}fn必收斂于其極限inf{fn}，即inf{fn}。

文獻[17]對混合優化算法的全局收斂性進行了詳細的分析，證明得出如下定理：

定理2如果某種算法同時具備以下兩個條件，則該算法最優序列依概率1全局收斂。

條件1在迭代最優解時，采用貪心策略保留精英，即：

其中，fBestk為比較k次后的最優適應度，X為第k+1次迭代后用來與fBestk比較的解。

條件2從任意一個非全局最優點X′轉移到與之對應的水平集L(Xr)={X|f(X)＜f(Xr),X∈S}的概率不為0，S表示整個搜索空間。

假設MSIMPA的目標函數f為求極小值，隨機采樣序列為，采樣點最優序列為，全局最優點為fBest。

證明MSIMPA不論原算法還是改進后的策略均遵循貪心策略，滿足定理2的條件1。

由定理1可知fkBest有極限，設nBest=inf{fBestk}≠fBest,則有fBestn＞fBest,且?k∈Z+,fBestk≥fBestn。因為原算法MPA最后收斂于頂級捕食者構成的精英矩陣，所以當X取值到精英周圍足夠小的鄰域時，必有P{L(X′)}=P{X|f(X)＜f(X′),X∈S}≠0（此處P{}·表示概率），故滿足條件2。

綜上，MSIMPA算法依概率1全局收斂，即P{Best}=1。其收斂速度受t分布隨機取值以及維度交叉有效性的影響，有效性越高收斂越快。

3 函數測試與數值分析

3.1 函數測試

為了檢驗本文提出的MSIMPA算法的有效性，選取了15個測試函數與MPA、MVO、PSO、MFO、WOA、GWO、ASO這7種算法進行求極小值仿真對比。測試函數中含有6個多維單峰函數F1～F6、6個多維多峰函數F7～F12和3個固定維度多峰函數，具體函數信息見表1。所有算法迭代次數均設置為500次，種群數量均為30個。多維測試函數維度為30、50維，固定維度函數F13為2維，F14、F15為4維。將8種算法分別獨立運行30次，分別計算30次運行的平均最佳適應度值和最佳適應度值的方差。優先根據平均適應度值（尋優精度）對算法性能進行排序，如果平均適應度相同，再根據方差和收斂速度排序。

表1測試函數Table 1 Test functions

本文繪制出50維時8種算法在5個單峰測試函數、5個多峰函測試數和2個固定維度測試函數下的迭代收斂曲線圖，見圖6。

如圖6所示，在求解F6、F8、F10、F11等函數時，MSIMPA的初始適應度更佳，表明混沌對立初始化可以有效提高初始種群質量。在求解多維函數F1、F2、F4、F7、F8和F10時都達到最優，精度顯著提升。其中F11具有多個局部最優峰值，且波谷內較為平緩，大多數算法很難找到其全局最小值，MPA算法雖然相對于其他幾種算法有略微優勢，但是尋優精度不夠，可見原算法考慮FADs的位置擾動并不能滿足需求。而MSIMPA在迭代開始階段，t分布變異含有全局搜索成分，收斂曲線迅速下降，迭代到90次左右時，結合和分組維度學習的作用，迭代曲線迅速收斂。由F8可知，MPA和WOA雖然也達到理論最小值，但是收斂速度明顯不如MSIMPA。F14～F15是固定維度函數，最優值非0，MSIMPA和MPA平均適應度均為最佳，但收斂速度上MSIMPA更快。同樣，在F9上也能進一步明顯體現出MSIMPA尋優精度高、收斂速度快的優勢。

3.2 數據分析

表2為30維時F1～F12的最終測試結果，表3為50維時F1～F12和固定維度時F13～F15的最終測試結果。通過表2和表3數據分析可知，無論是30維還是50維的情況下，MSIMPA算法的方差和平均適應度指標相較其他算法具有明顯優勢。

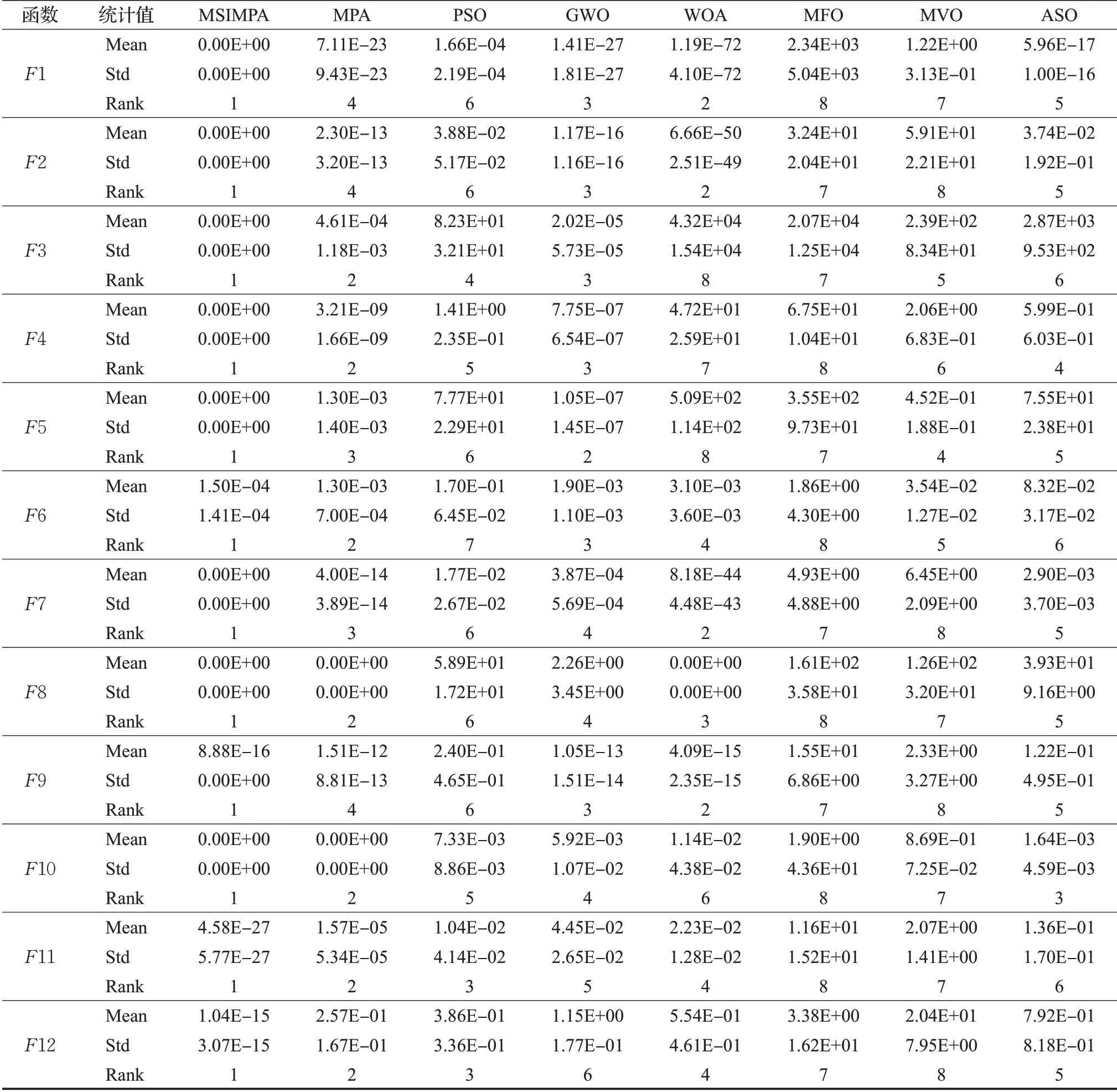
表2 30維函數測試數據Table 2 Test data of 30 dimensional functions

表3 50維及固定維度函數測試數據Table 3 Test data of 50 dimensional functions

表3 （續）

維度由30維提升到50維時，其余7種算法整體尋優性能均相對變差，而對于MSIMPA算法，維度變高以后，分組維度學習范圍也按比例變寬，在較大程度上可以減弱高維帶來的影響，在F1～F5、F7～F8和F10上依然可以達到理論極小值0，尋優精度遠高于MPA。雖然在少數幾個函數上，升高到50維時的MSIMPA尋優精度也有所降低，但仍然要優于其他對比算法。標準差體現出算法在求解中的穩定性，算法GWO、ASO隨著求解維度的增高，標準差明顯增加，說明這兩個算法求解高維度問題時穩定性較差。而MISCSA算法標準差相較于MPA、PSO、WOA等都低，說明算法的穩定性更好。

在30維和50維情況下，各算法排名差異不大，保持在前列的為MSIMPA、MPA、GWO，性能較差的為MVO、MFO。為了更直觀地分析各算法的尋優能力，繪制出圖7的排序雷達圖，算法性能曲線越靠近中間，則性能越優越。

由圖7可知，忽略MSIMPA算法，MPA算法在F1、F2、F5、F7、F9、F12、F13上分別被不同的算法超越，排名在2～4之間，可見原MPA算法雖然性能較佳，但仍存在一定的不足，而MSIMPA算法在15個測試函數中性能均為最佳。值得一提的是MVO在F13上表現出色，尋到了理論最優值，且收斂速度排在了第2位，方差排在第3位。

3.3 統計檢驗

Derrac等人在文獻[18]中指出，僅依靠平均值和標準差來比較算法的差異不夠嚴謹。獨立運行得到的平均適應度值和標準差，仍有一定概率出現較好的數據，從而影響算法之間的性能比較。想要對改進算法性能做評估，需要在統計學層面上來判斷不同算法整體指標的顯著性區別。因此，將8種算法分別在15個測試函數上獨立測試30次的結果作為樣本，在0.05的顯著性水平下分別對30維和50維以及固定維度函數的測試結果進行Wilcoxon統計檢驗，判斷7個對比算法的結果與MSIMPA的結果的顯著性區別。檢驗結果見表4和表5。

根據文獻[18]，當P＜0.05時可以被認為是拒絕零假設的有力驗證，說明所對比的兩種算法具有顯著性差異，P＞0.05則說明兩種算法的尋優結果在整體上是相同的。根據表4和表5中的結果，因為MPA求解函數F8、F10以及WOA求解函數F8，均與MSIMPA同時搜索到全局最小值0，所以該統計檢驗不適用，記為“NaN”。其中，50維情況下，MSIMPA與WOA只有在求解F10時可以認為無明顯差異，求解其余測試函數時均與其余所有對比算法有顯著區別。30維情況下，MSIMPA的P全部小于0.05，表明了算法的優越性在統計上是顯著的。

表4 30維時Wilcoxon統計檢驗結果Table 4 Wilcoxon statistical test results in 30 dimensions

表5 50維及固定維度時Wilcoxon統計檢驗結果Table 5 Wilcoxon statistical test results of 50 dimensions and fixed dimensions

4 MSIMPA優化無線傳感器網絡覆蓋

假設在邊長分別為L1和L2的矩形無線傳感器WSN檢測范圍內，隨機分布N個同構傳感器的節點，假設節點Zi的位置坐標為，每個節點的感知范圍是以該節點為中心，Rs為半徑的圓形區域，則將該圓形區域稱感知圓盤，Rs稱為感知半徑。為了便于建模計算，將感知圓盤離散為m×n個待覆蓋的目標點，目標點Cj的位置坐標為( )xj,yj，則目標點和傳感器節點的距離定義為：

若存在某個節點與目標點的距離小于或等于感知半徑Rs，則代表目標點已被傳感網絡覆蓋。基于0/1模型，將目標點被傳感器節點Zi感知的概率定義為[19]：

其中，Re為節點感知誤差；λ為感知衰減系數。當目標點被多個傳感器感知，則目標點的聯合檢測概率為：

該區域的覆蓋率為全部節點所覆蓋的目標點總數與區域內目標點總數的比值，定義為：

通過函數測試對比，MSIMPA和MPA算法的綜合能力領先于其他對比算法，且考慮到本文主要測試MPA算法的改進性能，故本文的WSN覆蓋優化只選擇MSIMPA和MPA算法進行對比。具體的實施步驟與第2.4節算法實施步驟基本相似，將覆蓋區域邊界長度設置為第2.4節算法中的尋優邊界，設種群中的個體維度為2N,則種群中的每個個體位置構成N個二維平面坐標，代表N個傳感器節點。算法邏輯上為搜尋最小值，欲求最大覆蓋率，將式（28）改為：

選取式（29）作為適應度函數，捕食者在搜尋獵物的時候不斷更新自己的位置，并在位置更新以后采用分組維度學習的方式對位置維度取長補短，可以較大程度上提升最優個體的位置精度。算法迭代結束后，得到式（29）的最小值，即可反向求出傳感器節點的最大覆蓋率。實驗參數設置如表6。

表6 參數設置Table 6 Parameter setting

當傳感器節點為30個時，MSIMPA和MPA的初始化覆蓋情況如圖8，紅點代表節點，圓圈代表感知圓盤。MPA采用隨機分布初始化，初始覆蓋率為53.92%，而MSIMPA算法采用混沌對立初始化，初始覆蓋率為65.23%，提高了約11個百分點，反映出混沌對立初始化的種群質量更高。

算法優化后的傳感器區域覆蓋結果如圖9所示。圖9（a）、（b）為30個節點時的覆蓋情況，MPA算法優化的覆蓋率為81.15%，MSIMPA算法優化的覆蓋率為87.03%。從圖9（a）中可以清楚地看到，MPA優化時覆蓋區域的邊緣和中心部位都有明顯的空缺，各個節點感知范圍重疊較為密集，圖9（b）中MSIMPA優化覆蓋的區域則更加均勻。圖9（c）、（d）為40個節點時傳感器區域的覆蓋情況，此時圖9（c）中MPA優化后的覆蓋率為90.61%，原點附近仍有較大盲區且重疊部分略多，圖9（d）中MSIMPA優化后的覆蓋率為96.55%，重疊部分有所改善且無明顯盲區。

為了使實驗更加準確，算法分別獨立運行30次，平均覆蓋率見表7。通過表7可知，MSIMPA的覆蓋率和初始覆蓋率都高于MPA。

表7 平均覆蓋率Table 7 Average coverage 單位：%

迭代曲線如圖10所示。圖10（a）中30個節點時，MSIMPA由于初始化質量更高，迭代曲線起點高且迅速上升，在120代時趨于穩定，MPA迭代曲線還處于上升階段，此時覆蓋率相差最大。在迭代到400代時，MSIMPA優化精度略微提高后再次穩定，這時處于迭代后期，t分布變異著重于局部開發，配合個體之間的維度學習，使得尋優精度進一步提高。40個節點時，相當于個體維度增加，MSIMPA的分組維度學習策略依然有效，無論是收斂速度還是覆蓋范圍，均明顯高于MPA算法的優化效果。

綜上所述，通過與不同節點在同等測試條件下的實驗結果對比，MSIMPA算法實現了更高的平均覆蓋率，節點分布更加均勻，覆蓋盲區和感知范圍重疊區面積更少，驗證了所提出改進策略的有效性。

5 結束語

為了進一步改進海洋捕食者算法的尋優性能，本文提出了MSIMPA算法。首先，在MPA算法中加入了混沌對立初始化，提高了初始種群質量。其次，加入了自適應t分布變異算子，增加算法逃逸出局部最優的能力。最后，對位置更新完畢的種群進行分組維度學習，增加算法的收斂速度和精度。將MSIMPA與其他7種算法在15個測試函數上測試對比，MSIMPA在求解高維單峰和多峰函數以及固定維度函數時，求解精度與收斂速度均有明顯優勢。并將MSIMPA在WSN覆蓋優化問題上與MPA算法進行對比，實驗結果進一步驗證了所提出改進策略的有效性。