物與信息混合驅動的帶返修生產系統性能分析
陳文沖 阮淵鵬 李建國 齊二石
1.杭州電子科技大學管理學院,杭州,310018 2.天津大學管理與經濟學部,天津,300072
0 引言
生產系統建模主要借助抽象化的數學模型、模型語言來描述生產系統的行為特征與變化規律,以識別瓶頸工序、在制品庫存等關鍵屬性,從而為優化和改善制造系統的性能、制定更加有效的生產控制與調度策略提供指導[1-2]。HUDSON等[3]基于ProModel仿真軟件構建了面向異步生產系統性能的分析模型。JIA等[4]應用分解和聚合算法構建了不可靠生產系統的性能分析模型。仿真模型能對復雜生產系統進行較好的建模與性能分析,但存在模型運行時間長的問題;數學模型則能有效避免仿真模型的缺點。有學者針對以實物流為核心的生產系統性能分析問題,建立了Flow models[5]、Markov Chain模型[4]。
隨著越來越多專業化信息工具的使用,以實物流為主的生產系統向以信息流與實物流(以下簡稱“兩流”)為核心的自動化、數字化、智能化生產系統轉變[6-8]。這種轉變提高了系統的精準決策能力,但也提高了系統的不確定性。基于自動化制造系統構建的CPS架構[9]和以數字孿生技術為核心的制造車間分層管控模式[10]對構建信息作用下的現代化生產決策與管控平臺具有重要作用,但它們難以識別系統運行過程中存在的問題,并制定相應的生產改善與控制策略來提高性能。
針對兩流混合驅動的數字化生產系統性能分析問題,本文以含返修閉環異步串聯生產系統為對象,研究建立系統穩態性能分析數學模型。首先,利用重疊分解法[11-12]將兩流混合驅動的串聯生產系統拆分成3個子裝配系統和1個混合生產系統(含裝配和拆卸兩類過程)。而后,通過前向遞歸和反向遞歸方法對4個子系統中的關鍵參數進行迭代分析,確定穩態條件下的生產系統總體性能,并通過數值實驗驗證模型的有效性。最后,以工業縫紉機自動化生產線為實例,進一步驗證模型的有效性,并識別生產系統瓶頸、不確定生產要素對系統生產率的影響等關鍵屬性。
1 問題描述
兩流混合驅動的含返修閉環異步串聯生產系統被廣泛用于玻璃、鋼鐵、芯片、裝配等領域[1,13]。該系統包括一條串聯生產線(主生產線)、一條或多條返修閉環線,以及多種類型的信息控制設備。主生產線包含檢驗工位或檢驗設備,不合格產品經過返修閉環后再次進入主生產線的前工序進行加工;返修線可有效地提高生產系統的總生產率,降低系統因工件廢棄造成的浪費,但提高了生產信息采集、分析與執行的復雜度。該生產系統主要存在兩類信息流:①根據歷史生產數據和需求數據,制定合理的生產計劃,生成實時的生產指令以自動控制生產系統的運行,控制關鍵設備的生產率,避免過量生產或產生大量的在制品庫存[14];②通過感知實時的工件質量數據,生成實時的返修指令以控制相應工序或設備對工件進行返修。復雜的生產系統結構和信息控制過程使面向該類生產系統的建模分析變得異常困難。
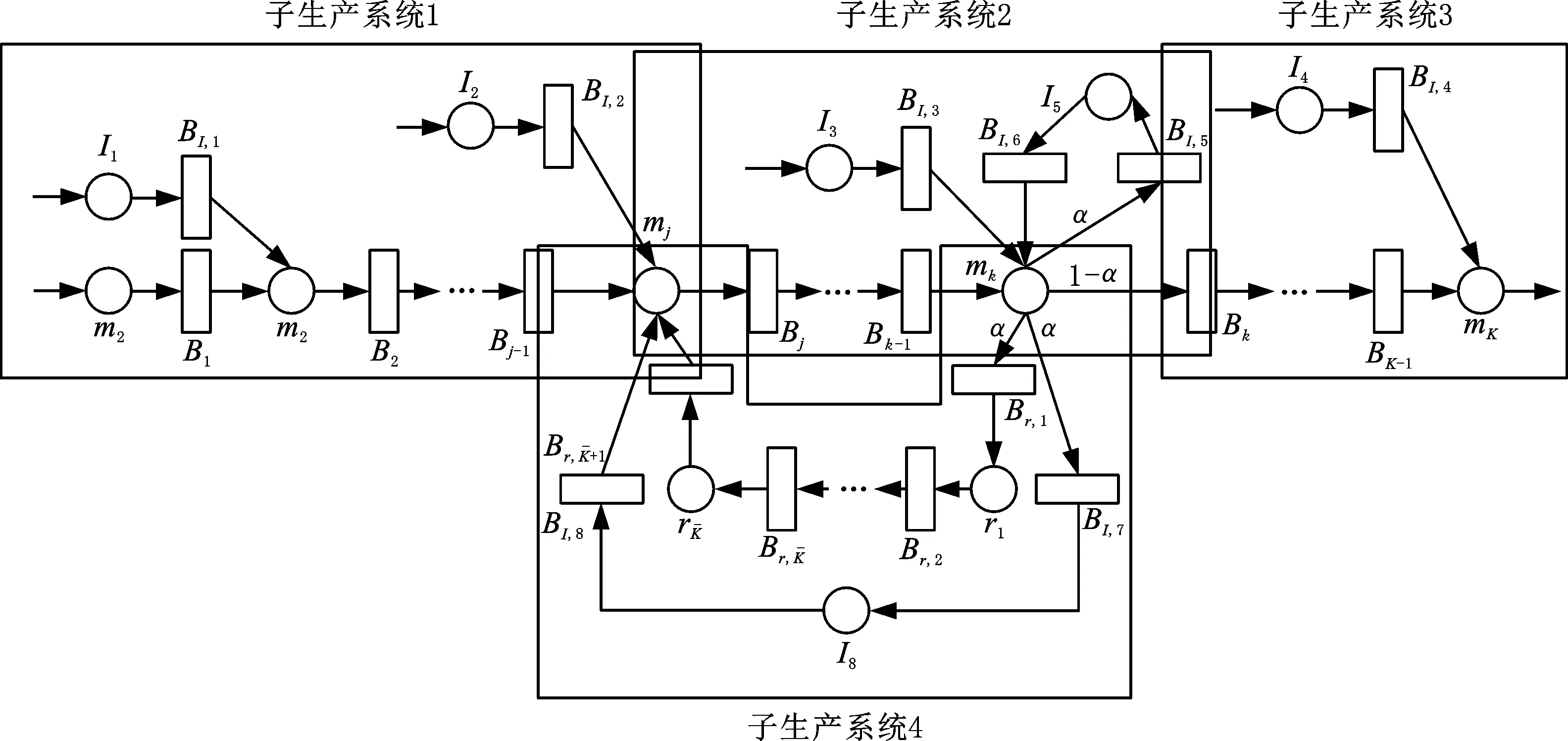
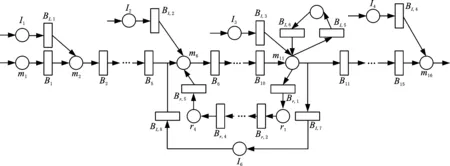
為降低運行總成本,兩流混合驅動的含返修閉環異步串聯生產系統只在關鍵工序配備信息控制設備,如圖1所示,圖中,實線箭頭表示生產系統工件流,虛線箭頭表示信息流。在該生產系統中,制造執行系統(MES)分別向信息控制設備I1~I4發送短期計劃指令。4臺信息控制設備分別根據生產計劃指令獨立控制機器m2、mj、mk、mK。信息控制設備I5、I6主要用來接收工件返修信息,并將處理后的工件返修信息反饋至機器mj和mk。為應對生產系統中的不確定因素,在加工機器間設立緩沖區,在機器與信息控制設備間均設立信息暫存區(主要用來存儲信息控制設備發送的信息指令),以避免隨機擾動事件造成不必要的生產系統性能損失。若信息暫存區的容量過大,系統動態調整信息控制指令的能力較弱;容量過小,則有可能因信息控制設備的隨機故障而影響整個系統的生產性能。
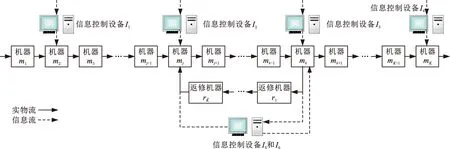
圖1 信息流與實物流混合驅動的含返修閉環異步串聯生產系統物理結構
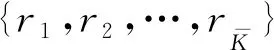
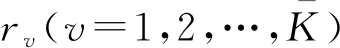
(2)信息控制設備Iz(z=1,2,…,6)有兩種狀態:運行狀態和故障狀態。當處于運行狀態時,信息控制設備單位時間向相應的機器(如設備I1對應機器m1、I2對應機器mj)發送cI,z(由具體的生產需求和生產參數決定)次信息控制指令;否則,不產生信息指令。
(3)機器mi的平均故障時間間隔與修復時間均是隨機變量,且服從參數為λi和μi的指數分布;返修機器rv的平均故障時間間隔與修復時間均是隨機變量,且服從參數為λr,v和μr,v的指數分布;信息控制設備Iz的平均故障時間間隔與修復時間均是隨機變量,且服從參數為λI,z和uI,z的指數分布。所有機器和信息控制設備的狀態相互獨立。
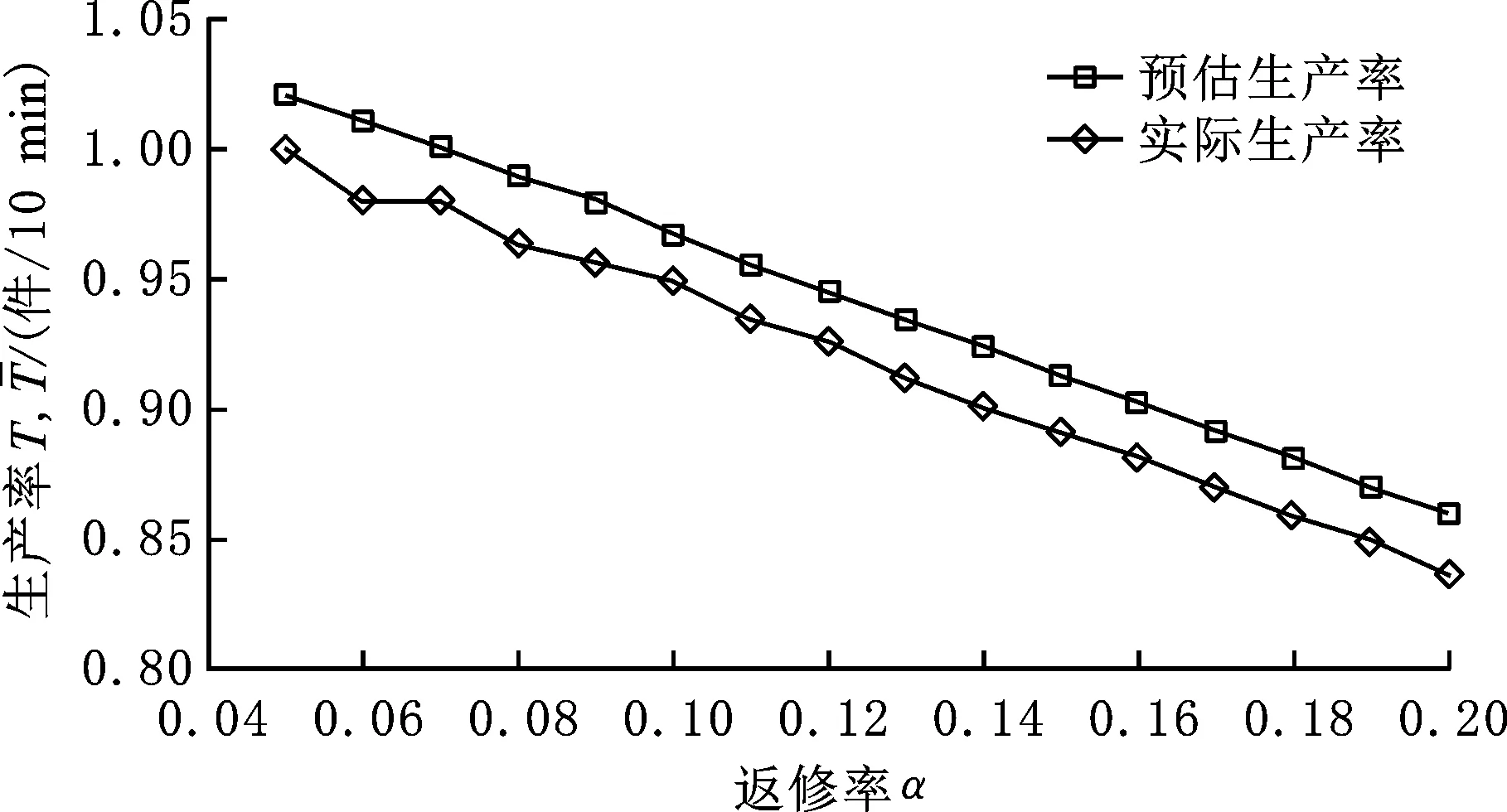
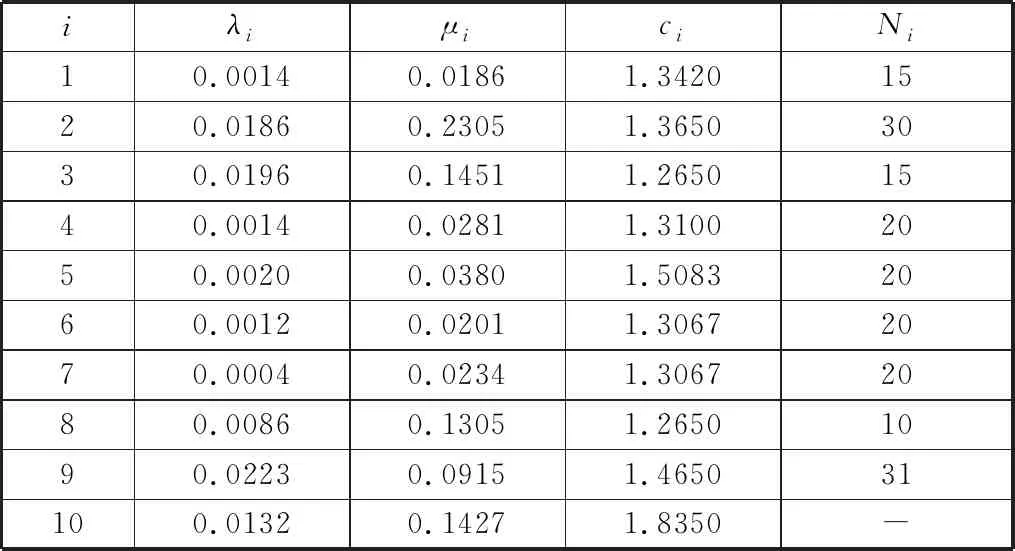
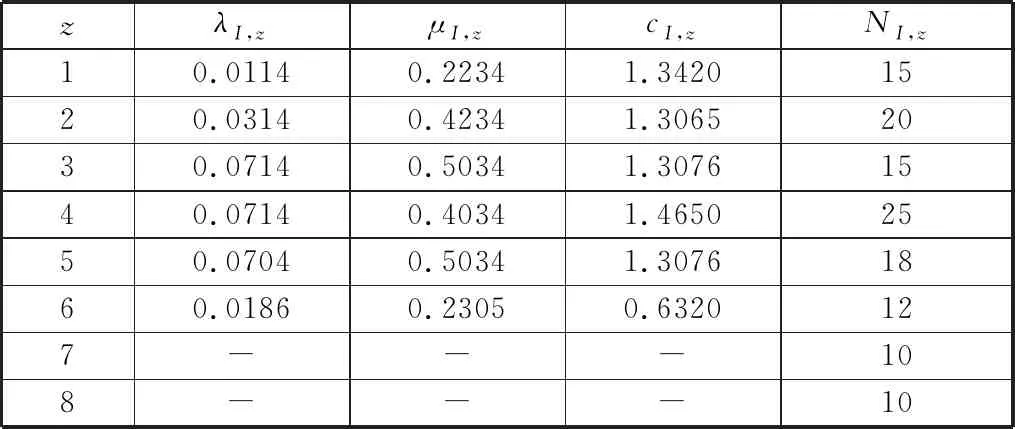
(4)緩沖區Bi、Br,v和信息暫存區BI,z對應的容量分別為Ni、Nr,v、NI,z,且0 (5)首臺機器或信息控制設備均不會處于饑餓狀態,最后一臺機器或信息控制設備均不會被堵塞;若某機器的任一緊前緩沖區或信息暫存區為空,則該機器或控制設備處于饑餓狀態,如緩沖區B1或BI,1為空,機器m2處于饑餓狀態;若某機器的任一緊后緩沖區或信息存儲區被填滿,則該機器處于堵塞狀態。 (6)工件被機器mk加工后,以概率α出現質量缺陷并通過返修系統進行返修。如圖2所示,缺陷工件將傳輸至緩沖區Br,1,其對應的修復信息將分別發送至信息暫存區BI,5和BI,7;如果緩沖區Br,1、信息暫存區BI,5和BI,7的任意一個被填滿,機器mk將被堵塞。 圖2 信息流與實物流混合驅動的含返修閉環異步串聯生產系統結構約簡圖 (7)與主生產線相比,返修閉環向機器mj供應半成品具有更高的優先級,如BI,8的返修信息比BI,2的計劃信息具有更高的優先級。 (8)生產系統是異步的,即至少存在兩臺加工速度不同的機器和信息控制設備。 (9)基于微分方法建立生產線性能分析模型,即無窮少的工件在Δt時間內被加工且被傳輸至對應的緩沖區,無窮少的生產指令在Δt時間內被生成且被傳輸至對應的信息暫存區。 上述假設中,假設(3)廣泛應用于生產系統的性能分析[12,15]。綜上所述,本文研究的問題可定義為:在上述假設條件下,在加工機器和信息控制設備均不可靠的情形下,建立兩流混合驅動的帶返修閉環異步串聯生產系統穩態性能分析模型,識別系統的關鍵屬性,為制定合理的改善對策提供指引。 單一信息控制下的串聯生產系統是含返修閉環異步串聯生產系統的基本組成單元,等同于將工件實物與加工信息進行裝配或將加工信息與工件實物進行拆卸的系統。因此,可采用重疊分解法[12]將該系統拆分成多個獨立的串聯子系統,并利用前向遞歸算法和反向遞歸算法建立子系統關鍵生產參數的遞歸方程。遞歸方程收斂時,可用收斂后的參數測算生產系統性能。 圖3為單一信息控制下的雙機器異步串聯生產系統的結構約簡圖,信息控制設備I1可根據工件需求生成最優的生產控制指令,通過實時控制機器m2的生產節奏,防止過量生產。根據重疊分解原理,圖2所示的生產系統可以拆分成2條串聯的子生產系統(m1,B1,V2,1)和(I1,BI,1,V2,2),其中,V2,1、V2,2為根據m2拓展的虛擬機器,它們的生產參數與m2相同。 圖3 單一信息控制下的雙機器異步串聯生產系統結構 (2)緩沖區B1在第n+1步為空的概率為 (1) (4)緩沖區BI,1在第n+1步為空的概率為 (2) (3) 多臺機器組成的串聯生產系統可視為加工信息與對應工件組合的裝配系統(圖4),以及加工信息與工件實物拆分的拆卸系統(圖5)。本節重點通過前向遞歸和反向遞歸算法,建立多工序裝配系統的性能分析模型。根據2.1節所示的重疊分解原理,將圖4所示的系統拆分成上層子系統(I1,BI,1,VK,1)和下層子系統(m1,B1,m2,B2,…,mK-1,BK-1,VK,2)。定義虛擬機器VK,1和VK,2來計算緩沖區BI,1和BK-1為空的概率,則分解后的上層子系統和下層子系統的聚合迭代可通過對虛擬機器生產能力的遞歸來實現,詳細的參數遞歸過程如下: 圖4 多機器異步裝配系統結構約簡圖 圖5 多機器異步拆卸系統結構約簡圖 (2)上層生產系統中信息控制設備I1的堵塞率bI,1(n+1)、虛擬機器VK,1的饑餓率sK,1(n+1)分別為 (4) 其中,eI,1、eK分別表示設備I1和mk的不可靠度。緩沖區BI,1在第n+1步為空的概率為 (4)下層生產系統的機器的堵塞率bi(n+1)、反向遞歸生產速度ci,b(n+1)、饑餓率si(n+1)和前向遞歸生產速度ci,f(n+1)分別為 (5) 基于上述過程,可推斷出遞歸過程(即步驟(1)~步驟(4))收斂且具有以下屬性: (2)解的唯一性。上述極限值是遞歸過程對應穩態方程的唯一解。 (3)系統的穩態生產能力。系統的穩態生產能力計算公式為 (6) 將上述遞歸迭代方程中的機器饑餓概率sI,1(n)、sM(n)用阻塞率b1(n)、bI,1(n)替代,即可建立適用于圖5所示拆卸系統的性能估計模型。 (a)帶返修閉環異步串行生產系統結構分解 (7) 其次,定義子生產系統3中mK的虛擬機器VK,1、VK,2,則該系統可進一步拆分成子系統{Vk,2,mk+1,…,VK,1}和{I5,VK,2}。此時,子系統{Vk,2,mk+1,…,VK,1}中虛擬機器Vk,2、VK,1的生產速度ck,2和cK,1,子系統{I5,VK,2}中虛擬機器VK,2的生產速度cK,2可通過如下公式計算得到: (8) 同理,定義子生產系統1中機器m2的虛擬機器V2,1、V2,2,虛擬機器Vj,2的虛擬機器Vj,2,1、Vj,2,2,則該系統可進一步拆分成子系統{m1,V2,1,…,Vj,2,1}、{I1,V2,2,…,Vj,2,1}和{I2,Vj,2,2}。此時,子系統{m1,V2,1,…,Vj,2,1}中虛擬機器V2,1、Vj,2,1的生產速度c2,1和cj,2,1、子系統{I1,V2,2,…,Vj,2,1}中虛擬機器V2,2的生產速度c2,2,子系統{I2,Vj,2,2}中虛擬機器Vj,2,2的生產速度cj,2,2可通過如下公式計算得到: (9) 最后,定義子生產系統2中Vk,3的虛擬機器Vk,3,1、Vk,3,2、Vk,3,3,則該系統可進一步拆分成子系統{Vj,3,mj+1,…,Vk,3,1}、{I3,Vk,3,2}和{Vk,4,I4,Vk,3,3}。此時,子系統{Vj,3,mj+1,…,Vk,3,1}中虛擬機器Vk,3,1的生產速度ck,3,1、子系統{I3,Vk,3,2}中虛擬機器Vk,3,2的生產速度ck,3,2、子系統{Vk,4,I4,Vk,3,3}中虛擬機器Vk,3,3的生產速度ck,3,3可通過如下公式計算得到: (10) 根據式(7),可建立子生產系統4相關參數的遞歸方程: (11) 上述遞歸過程的初始條件為 bk,r,1(0)=bk,I,5(0)=bk,I,7(0)=bj,j(0)=1 ck,1,1(0)=ck,1,2(0)=αck 根據式(8),建立子生產系統3各相關參數的遞歸方程: (12) 其中,sK,K-1(n)為機器mK在第n次迭代中由緩沖區BK-1引起饑餓的概率,bk,k(n)為機器mk在第n次迭代中由緩沖區Bk引起堵塞的概率,sK,I,4(n)為機器mK在第n次迭代中由緩沖區BI,4引起饑餓的概率。 上述遞歸過程的初始條件為 sK,I,4(0)=0 ck,2(0)=(1-α)ck 同理,根據式(9),建立子生產系統1各相關參數的遞歸方程: (13) 其中,cj-1,1,f(n+1)、cj-1,2,f(n+1)分別為機器mj-1在生產線{m1,V2,1,…,Vj,2,1}和{I1,V2,2,…,Vj,2,1}中的前向遞歸值,s2,1(n)為機器m2在第n次迭代中由緩沖區B1引起饑餓的概率,s2,I,1(n)為機器m2在第n次迭代中由緩沖區BI,1引起饑餓的概率,sj,j-1,1(n)為機器mj在第n次迭代中由生產線{m1,V2,1,…,Vj,2,1}中的緩沖區Bj-1引起饑餓的概率,sj,j-1,2(n)為機器mj在第n次迭代中由生產線{I1,V2,2,…,Vj,2,1}中的緩沖區Bj-1引起饑餓的概率,sj,I,2(n)為機器mj在第n次迭代中由緩沖區BI,2引起饑餓的概率。 上述遞歸過程的初始條件為 sI,1(0)=0 sj,I,2(0)=0 最后,根據式(10),建立子生產系統2各相關參數的遞歸方程: (14) 遞歸過程的初始條件為:bk,I,5(0)=1,ck,3,3(0)=ck。 基于上述遞歸迭代過程,可推斷出該帶返修閉環的異步串聯生產系統關鍵屬性: (1)4.1節的參數遞歸迭代方程均收斂于相應的常數。 (15) 根據不同參數的取值范圍,選取近2300個數值組合進行數值實驗。為對比分析模型的性能,基于FlexSim 17.2同步建立對應仿真模型。每個計算樣本分析模型的精確性可表示為 (16) (a)不同K值下的分析模型性能測算誤差 圖8 不同α對應的生產率 表1 數值實驗中機器mi和緩沖區Bi有關的生產參數 表2 數值實驗中返修機器rv和緩沖區Br,v有關的生產參數 表3 數值實驗中信息控制設備Iz和緩沖區BI,z有關的生產參數 由上述數值分析結果可知,本文構建的分析模型可有效測算混合驅動的含返修閉環異步串聯生產系統的性能。基于此模型可進一步分析該系統的關鍵屬性,如瓶頸設備識別、因信息不確定帶來的生產系統性能損失、帶信息驅動機制和不帶信息驅動機制的生產系統庫存水平差異等。 本節以工業縫紉機數字化生產系統為實例驗證分析模型的有效性。如圖9所示,該生產系統包含1條主生產線和1條返修閉環,主生產線中的工序和返修線中的工序均是異步的,且會發生隨機失效。工序平均故障間隔時間和修復時間均服從指數分布。信息系統對關鍵工序進行監控,采集并分析實時生產過程的數據。考慮數據保密性,本節對實例的結構和參數進行了適當的簡化,但簡化后的參數不影響模型的實用性。該生產系統主要包含三大類工藝過程:機加工(工序1~工序5)、噴漆(工序6~工序11)、裝配(工序12~工序16)。返修線開始于工序11(產品測試工位)。不合格產品從工序11流出,進入返修線,完成返修操作后重新流入工序6。無缺陷產品將從工序11直接傳送至工序12。產品在工位之間的傳輸通過傳送帶實現。MES通過信息控制設備控制生產系統中的關鍵工序即工序2、6、11、16的速度,實現按需生產和控制在制品庫存。工序11對應的信息控制設備可采集實時的產品質量信息,MES對采集到的質量信息進行加工處理后,生成產品返修信息并傳輸給該控制設備。該控制設備根據接收的返修信息分別控制工序6和工序11的加工過程。圖9所示的縫紉機生產系統可約簡成網絡結構圖(圖10)。生產系統加工參數、緩沖區容量、信息暫存區容量等信息如表4~表6所示。生產系統的工件返修率α=0.14。根據式(11)~式(14)可計算出該生產系統的穩態生產率。分析模型測算的生產率近似值為384件/天。與實際數值相比,該模型的測算誤差為4.2340%。生產需求為116件/天時,信息控制設備生成信息控制指令的速率為116次/天。此時分析模型的測算誤差僅為3.9872%。誤差在可接受的范圍內,可用該模型分析縫紉機生產系統的穩態性能與關鍵屬性。 圖9 工業縫紉機數字化生產系統物理結構圖 圖10 工業縫紉機數字化生產線構約簡圖 表4 工業縫紉機數字化生產線機器mi和緩沖區Bi有關的生產參數 工序瓶頸識別對提高生產系統的性能具有重 表5 工業縫紉機數字化生產線返修機器rv和緩沖區Br,v有關的生產參數 表6 工業縫紉機數字化生產線信息控制設備Iz和緩沖區BI,z有關的生產參數 表7所示為參數λi(?i)、λI,z(?z)分別增大0.0002或0.0004時的系統穩態生產率。工序m7、m12是該數字化生產系統的瓶頸工序。生產管理者若要制定改善對策,提高生產系統性能,應重點提高工序m7和m12的性能,制定對策以延長工序的平均故障間隔,縮短工序故障修復時間,提高加工速率等。 表7 不同λi或λI,zλi值下生產系統的性能 信息控制設備對生產系統性能有顯著影響的不確定要素如下:①信息控制設備的可靠性;②信息控制設備cI,5、cI,6對實時缺陷信息反饋的延遲。信息控制下的生產系統存在很多造成實時決策信息延遲的因素,這些延遲可能會使相應的信息控制設備變成整個生產系統的瓶頸,影響系統總體性能。本節通過改變參數eI,z(z=1,2,3,4)和信息決策效率cI,z(z=5,6)來設置不同的數值實驗,以觀測信息控制設備的不確定要素對生產系統性能的影響。如圖11所示,改變eI,z時,信息控制設備I2有可能將轉變成生產系統的瓶頸設備。當設備可靠性eI,1<0.68或eI,3<0.66或eI,4<0.68時,或當信息決策效率cI,5<0.50或cI,6<0.50時,信息控制設備的引入會顯著降低生產系統性能。因此,企業在推廣數字化生產線應用的同時,不能僅關注信息控制設備在降低在制品庫存、防止過量生產的積極作用,也應重點考慮信息控制設備不可靠性對生產系統總體性能的影響。圖11a中,信息控制設備I2的可靠性對生產率的影響最大,其次為I4、mI和I3。 (a)不同eI,z對應的系統生產率 本文以混合驅動的含返修閉環異步串聯生產系統為研究對象,通過重疊分解法、前向遞歸與反向遞歸迭代算法,建立了該系統穩態下的性能分析模型,識別并分析了系統的關鍵屬性,結合含返修閉環異步串聯生產系統的物理結構,設計了多組數值實驗并分別通過仿真模型和本文構建的分析模型測算每組實驗對應的生產系統穩態生產率。實驗結果表明,本文構建的分析模型穩態生產率測量誤差大多數情況都在5%以下,分析模型有效。而后,將分析模型應用于測算實際工業縫紉機數字化生產系統的穩態性能,識別該實際生產系統瓶頸并評價不可靠信息控制設備對系統總體性能的影響。實例研究結果表明,當信息控制設備不可靠性低于某個閾值時,該信息控制設備將轉變整個生產系統運行的瓶頸。因此,面向數字化、智能化生產系統的設計與改善,應綜合考慮實物流和信息流的影響。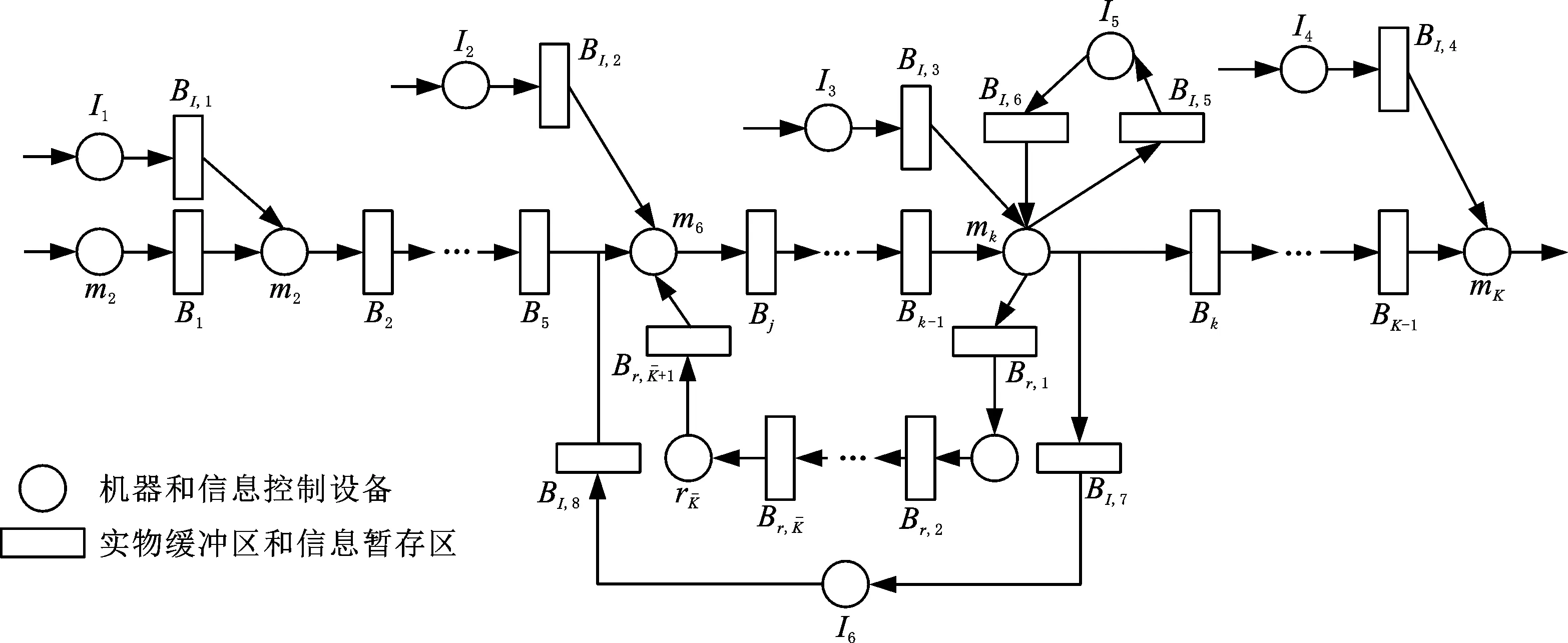
2 單一信息控制下的異步串聯生產系統性能分析模型
2.1 雙機器異步串聯生產系統性能的分析模型
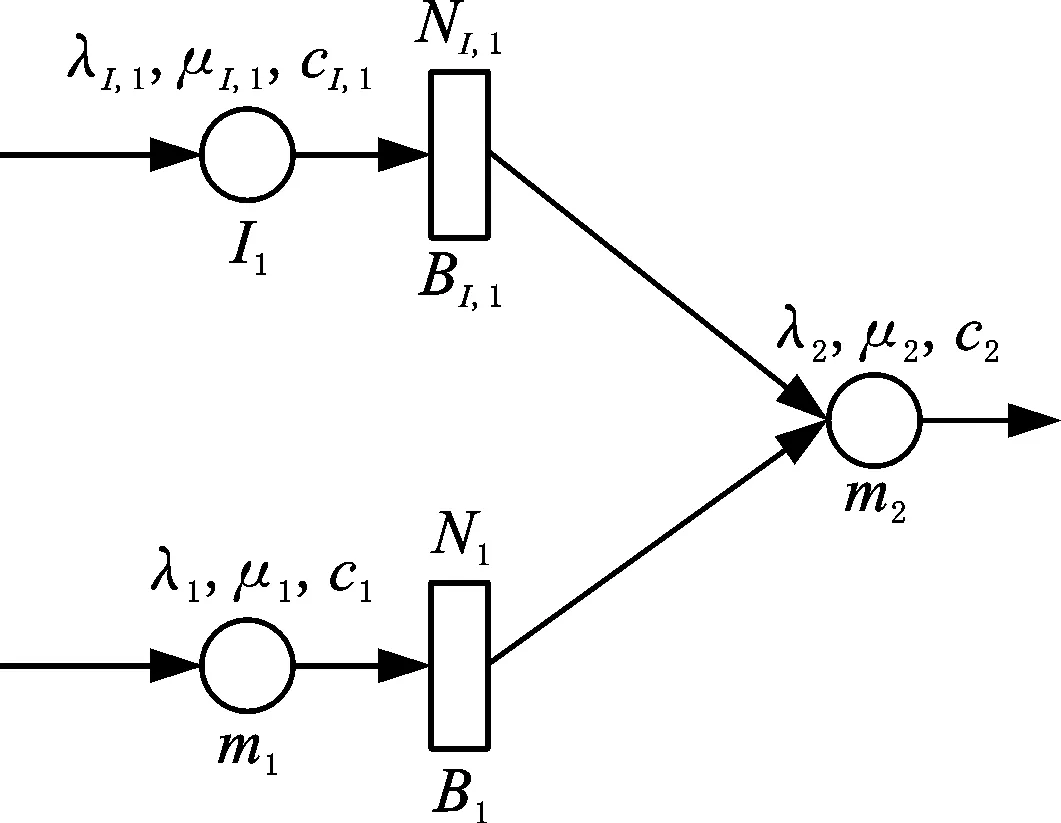
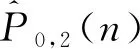
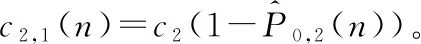




2.2 多機器異步串聯生產系統的性能分析





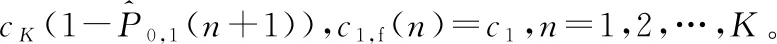
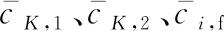
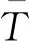
3 混合驅動的含返修閉環異步串聯生產系統的結構分解

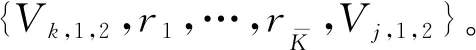
4 基于遞歸迭代算法的含返修閉環異步串聯生產系統性能分析模型
4.1 狀態轉移規則分析與建模
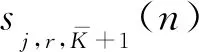
4.2 模型收斂性分析
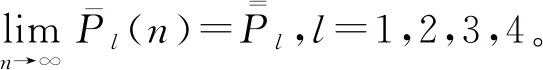

4.3 模型精確性分析

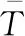
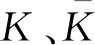

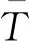

5 實例分析


5.1 生產系統瓶頸識別


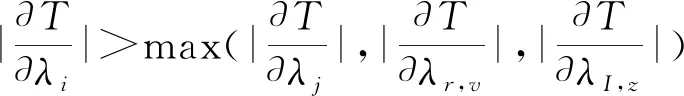

5.2 信息控制設備對生產系統生產率的影響

6 結語

