Riemann–Hilbert approach and N double-pole solutions for a nonlinear Schr¨odinger-type equation
Guofei Zhang(張國飛) Jingsong He(賀勁松) and Yi Cheng(程藝)
1School of Mathematical Sciences,University of Science and Technology of China,Hefei 230026,China
2Institute for Advanced Study,Shenzhen University,Shenzhen 518060,China
We investigate the inverse scattering transform for the Schr¨odinger-type equation under zero boundary conditions with the Riemann–Hilbert(RH)approach. In the direct scattering process,the properties are given,such as Jost solutions,asymptotic behaviors,analyticity,the symmetries of the Jost solutions and the corresponding spectral matrix. In the inverse scattering process,the matrix RH problem is constructed for this integrable equation base on analyzing the spectral problem. Then,the reconstruction formula of potential and trace formula are also derived correspondingly. Thus,N double-pole solutions of the nonlinear Schr¨odinger-type equation are obtained by solving the RH problems corresponding to the reflectionless cases. Furthermore,we present a single double-pole solution by taking some parameters,and it is analyzed in detail.
Keywords: Schr¨odinger-type equation, Riemann–Hilbert problem, zero boundary conditions, N double-pole solitons
1. Introduction
In recent decades, nonlinear partial diferential equations are often used to describe natural phenomena and play a significant role in mathematics and physics,which have attracted much attention in soliton theory and integrable systems.[1–8]The inverse scattering transformation is an important method to study nonlinear partial differential equations. Then, the Riemann–Hilbert (RH) problem is widely adopted to solve nonlinear integrable models, and the solution is an improved version of inverse scattering transformation.[9,10]However,many works focused on studies of nonlinear systems in the case that all discrete spectra are simple. At present, there are some works about the double pole solutions to nonlinear integrable equations.[11–18]Moreover, the higher-order pole solutions have also been studied in some papers.[19–23]In this paper, we study the inverse scattering transform for the Schr¨odinger-type equation under zero boundary conditions(ZBCs)with the RH approach.
As is well known,the nonlinear Schr¨odinger(NLS)equation
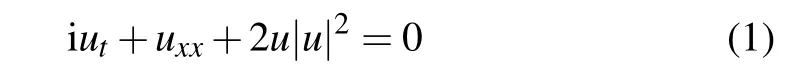
comes from a wide range of practical backgrounds, such as deep water waves, plasma physics, quantum field theory, and other fields.[24–27]Based the different concerns of nonlinear phenomena,there are three known modifications of NLS equations including different nonlinear terms by comparing with the NLS equation(1),such as the KN equation,the CLL equation and the GI equation, which are also called the DNSI,DNSII,and DNSIII,[28–35]etc.
A new Schr¨odinger-type equation was proposed in Ref.[36],

where the asterisk* denotes the complex conjugation. It is an extension of the NLS equation by adding two new terms including two derivates. It is non-trivial to preserve the integrability of the NLS equation by adding proper terms to reach Eq.(2). Then,the Lax pair,a 2×2 matrix spectral problem,is given via the prolongation structure theory,

σ3=diag(1,-1), andz ∈C is a spectral parameter, andNsoliton solutions of the equation with ZBCs are expressed explicitly via the RH approach in Ref. [37]. Furthermore,Nsoliton solutions of this equation under NZBCs are expressed explicitly via the RH approach in Ref.[38]. However,for the double-pole soliton solutions of this equation under ZBCs, it is rarely studied. Thus, we will considerNdouble-pole soliton solutions of the new integrable nonlinear Schr¨odinger-type(NLST)equation with ZBCs via the RH approach.
An outline of this paper is as follows. In Section 2,starting from the Lax pair of Eq.(2)and the ZBCs,one can obtain Jost solutions. Then, analyticity, symmetries and asymptotic behaviors associated with eigenfunction and scattering matrix are realized. In Section 3,on the basis of the former analysis,the matrix RH problem is constructed for this integrable equation(2),and the reconstruction formula of potential and trace formula are also derived correspondingly. Furthermore,Ndouble-pole solutions of the nonlinear Schr¨odinger-type equation are obtained by solving the RH problems corresponding to the reflectionless case, and an example is given, which is discussed in the case ofN=1. Finally,we present some summary and discussions.
2. The direct scattering with ZBCs
In this section, we analyze the direct scattering with ZBCs,

and the case of double poles for the Lax pair of Eq.(2).
2.1. Spectral analysis
Under the boundary condition (5), the Lax pair will be changed into

where the Lie bracket[M,N]=MN-NM. Moreover,one can obtain the full derivative form and the following Volterra integral equations:


Proposition 1 Supposeu(x,t)∈L1(R) and the Jost solutionsφ±(x,t;z) (φ±(x,t;z)=(φ±1,φ±2)), we have the following results:
(1)Eq.(3)has only a solutionφ±(x,t;z), which can satisfy Eq.(7)onΣ.
(2)φ+1(x,t;z) andφ-2(x,t;z) can be analytically extended toD+and continuously extended toD+∪Σ.
(3)φ+2(x,t;z) andφ-1(x,t;z) can be analytically extended toD-and continuously extended toD-∪Σ.
Here, the modified Jost solutionsμ±(x,t;z) possess the same properties asφ±(x,t;z).
Proof The proposition was given in,e.g., Refs. [16,37,38]. It can easily be given the analyticity and continuity ofμ±(x,t;z)by the relation(9).
Proposition 2 The Jost solutionsφ±(x,t;z) can satisfy the Lax pair(3)of the NLST equation(2).
Proof Notice that

by Liouville’s formula and the zero-curvature conditionUt-Vx+[U,V]=0,one can knowφ±(x,t;z)-Vφ±(x,t;z)solves thex-part(3). Based on the above analysis,there are two matricesQ±(t;z)satisfying
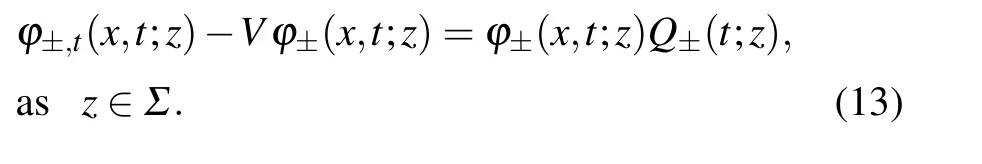
Using the transformation(9),one can obtainμ±(x,t;z)~IandQ±(t;z)=0 asx →±∞, which means thatφ±(x,t;z) solves thet-part(3).
2.2. Scattering matrix and reflection coefficients
In this subsection,the scattering matrix and reflection coefficients are introduced. Sinceφ+(x,t;z) andφ-(x,t;z) are two fundamental matrix solutions of the Lax pair (3), there exists a linear relation betweenφ+(x,t;z)andφ-(x,t;z):
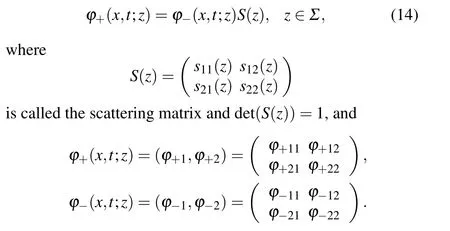
Then,it follows from Eq.(14)thatsi j(z)(i,j=1,2)have the Wronskian representations:

Proposition 3 Supposeu(x,t)∈L1(R). Here,s11(z) is analytic inD+and continuous onD+∪Σ,whiles22(z)is analytic inD-and continuous onD-∪Σ. In addition,s12(z)ands21(z)are continuous inΣ.
Proof From Proposition 1 and Eq.(15),it is easy to give the proof of the proposition. Note that we can not exclude the possibility of the existence of the zero point alongΣ, in the case of ZBCs,which can lead to the so-called real singularity spectrum. Now we only consider potential functions without spectral singularities.[39]
2.3. Symmetry properties
Proposition 4U(x,t;z),V(x,t;z), Jost solutions, modified Jost solutions,scattering matrix and reflection coefficients possess two types of symmetry.
(1)The first symmetry reduction:
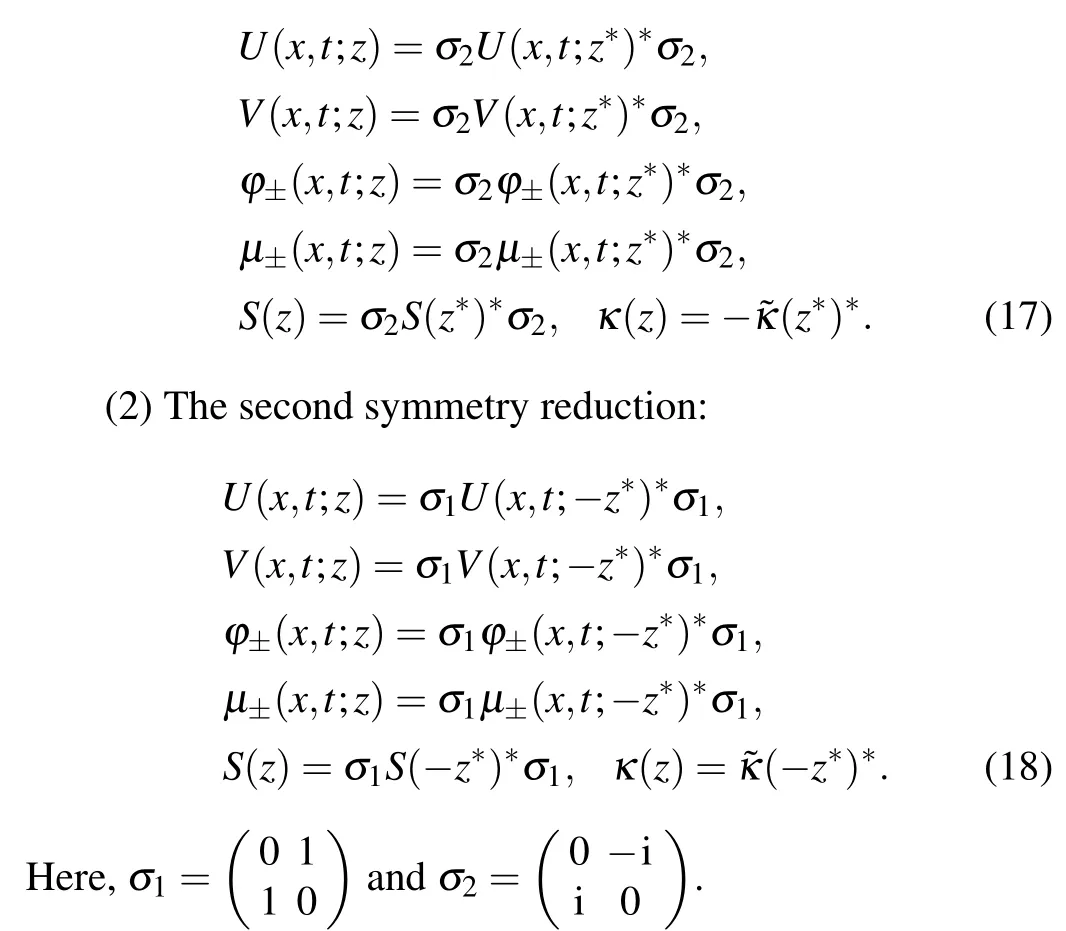
Proof The similar properties were given in Refs.[37,38],which have been proved by many researchers.[11,16,31,40]
2.4. Asymptotic behaviors
To deal with the RH problem,we must discuss the asymptotic behavior of the modified Jost solutions and scattering matrix asz →∞in this subsection.
Proposition 5 The asymptotic behaviors of the modified Jost solutions can be expressed as


where (μ(n))offdenotes the off-diagonal parts of the matrix.This completes the proof of the proposition.
Proposition 6 The asymptotic behavior for the scattering matrix is given by

2.5. Discrete spectrum with double zeros


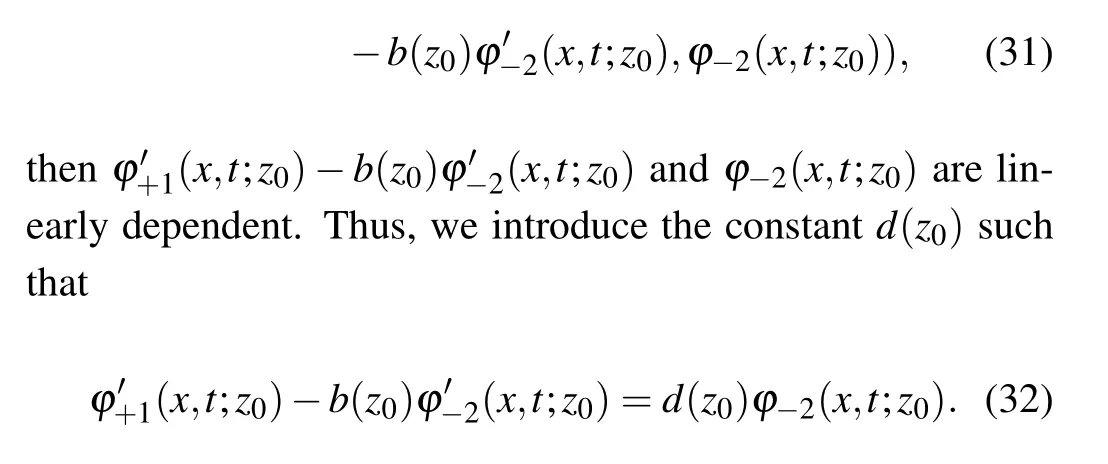
Furthermore, letφ+1(x,t;z0)ands11(z)carry out expansion atz=z0,one has

For simplicity of presentation,we denoteA(z0)andB(z0)such that

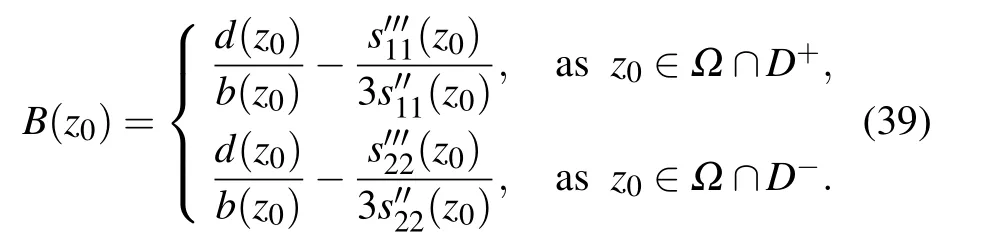
It follows that

Proof Considering Eqs.(38)and(39),from Proposition 4 one can show this proposition.
3. Inverse problem with ZBCs and double poles
In order to study the inverse problem with ZBCs and to obtain theNdouble-poles solutions of the Eq. (2), we must establish and solve an RH problem based on the above discussions.
3.1. The matrix Riemann–Hilbert problem



Then,one can obtain the soultion(54)by using Plemelj’s formula.
3.2. Reconstruction formula of the potential
In the subsection,our aim is to obtain the reconstruction formula. The first step is to give

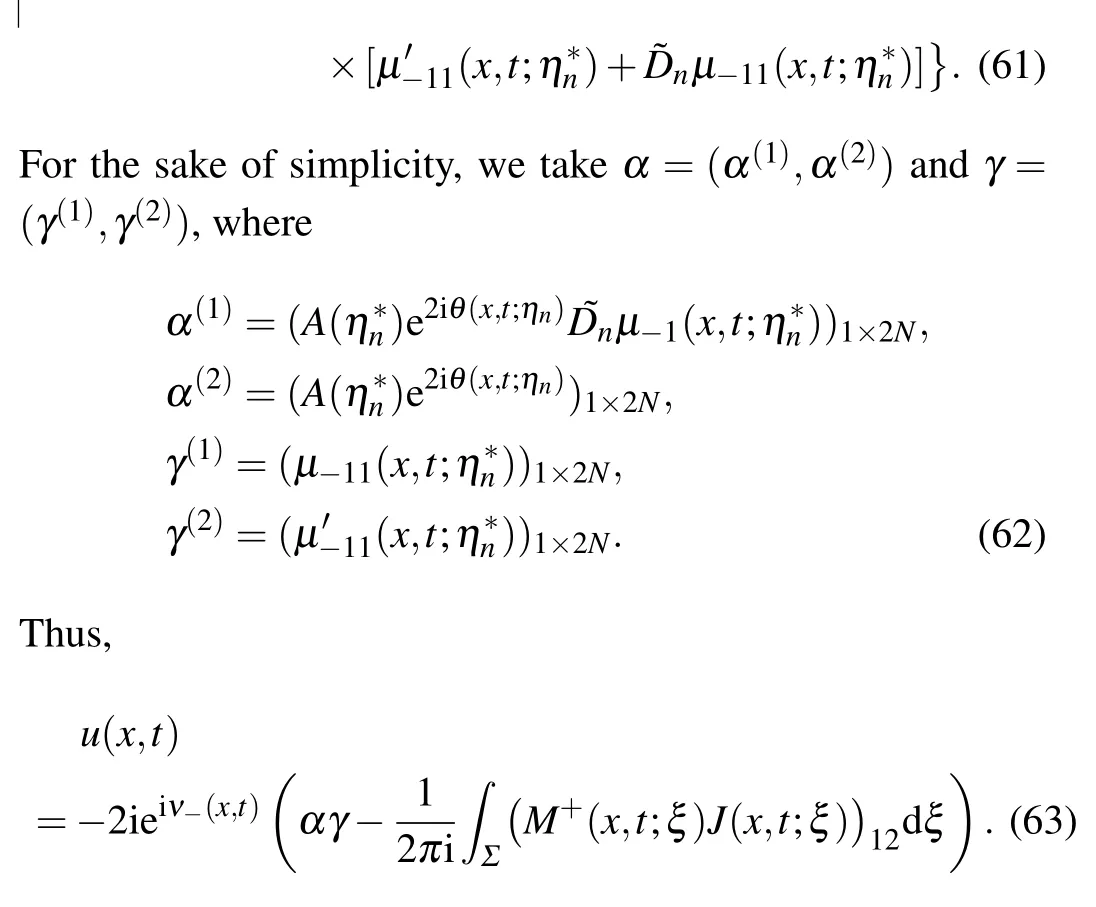
3.3. Trace formulae


3.4. Reflectionless potential: double-pole solitons


from Eqs.(67)and(11)asx →∞,and obtain
by pluggingγback into the formula of the potential, which can be given by using Eq. (73). Then, the exact form of reflectionless potential can be given by combining Eq.(72)with Eq.(74). This proof is completed.
From the above analysis, it is easy to obtainNdoublepole soliton solution of the NLST equation (2) under ZBCs via Eq. (68). For example, the single double-pole solution is given in Fig. 1. Here, Figs. 1(a)–1(c) show the dynamical characteristics of double-pole soliton of the new Schr¨odingertype equation fort=-3,0,3, and the nonlinear phenomena is caused by two bright-solitons bumping into each other approximatively.
4. Summary and discussion
In this work, we mainly investigate a new Schr¨odingertype equation(NLST)with double zeros of analytical scattering coefficients, which is regarded as a new extension of the classical NLS equation,under ZBCs via the RH approach.For the direct scattering problem and the inverse scattering problem, we not only discuss the key properties including the analyticity,symmetries,asymptotic behaviors and discrete spectrum, but also construct the matrix RH problem via analyzing the spectral problem of the lax pair, and the reconstruction formula of potential, and trace formula are also derived correspondingly. Therefore, the expression ofNdouble-pole soliton solution for the NLST equation (2) is given. Furthermore,an example is given when taking parametersA(η1)=1,B(η1)=1,η1=1+(1/2)i,and the solution is also analyzed in detail. In our future work, we will consider this equation under nonzero boundary conditions via the RH approach,and study the long-time asymptotic behavior of the solution for the equation via the Deift–Zhou nonlinear steepest descent method. Moreover, the mathematical structure and physical properties of this equation are also necessarily studied.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 12071304 and 11871446) and the Guangdong Basic and Applied Basic Research Foundation(Grant No.2022A1515012554).
- Chinese Physics B的其它文章
- Microwave absorption properties regulation and bandwidth formula of oriented Y2Fe17N3-δ@SiO2/PU composite synthesized by reduction–diffusion method
- Amplitude modulation excitation for cancellous bone evaluation using a portable ultrasonic backscatter instrumentation
- Laser-modified luminescence for optical data storage
- Electron delocalization enhances the thermoelectric performance of misfit layer compound(Sn1-xBixS)1.2(TiS2)2
- TiO2/SnO2 electron transport double layers with ultrathin SnO2 for efficient planar perovskite solar cells
- Sputtered SnO2 as an interlayer for efficient semitransparent perovskite solar cells

