Topological superconductivity in Janus monolayer transition metal dichalcogenides

Xian-Dong Li(李現東) Zuo-Dong Yu(余作東) Wei-Peng Chen(陳偉鵬) and Chang-De Gong(龔昌德)

1National Laboratory of Solid State Microstructure,Department of Physics,Nanjing University,Nanjing 210093,China

2School of Information and Electronic Engineering,Zhejiang Gongshang University,Hangzhou 310018,China

3Shenzhen Institute for Quantum Science and Engineering,Southern University of Science and Technology,Shenzhen 518055,China

4Center for Statistical and Theoretical Condensed Matter Physics,Zhejiang Normal University,Jinhua 321004,China

5Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China

The Janus monolayer transition metal dichalcogenides(TMDs)MXY (M=Mo,W,etc.and X,Y =S,Se,etc.) have been successfully synthesized in recent years. The Rashba spin splitting in these compounds arises due to the breaking of out-of-plane mirror symmetry. Here we study the pairing symmetry of superconducting Janus monolayer TMDs within the weak-coupling framework near critical temperature Tc, of which the Fermi surface (FS) sheets centered around both Γ and K (K′) points. We find that the strong Rashba splitting produces two kinds of topological superconducting states which differ from that in its parent compounds. More specifically,at relatively high chemical potentials,we obtain a timereversal invariant s+f+p-wave mixed superconducting state,which is fully gapped and topologically nontrivial,i.e.,a Z2 topological state. On the other hand,a time-reversal symmetry breaking d+p+f-wave superconducting state appears at lower chemical potentials. This state possess a large Chern number|C|=6 at appropriate pairing strength,demonstrating its nontrivial band topology. Our results suggest the Janus monolayer TMDs to be a promising candidate for the intrinsic helical and chiral topological superconductors.

Keywords: topological,superconductivity,Janus,transition metal dichalcogenides(TMDs)

1. Introduction

Topological superconductors (TSCs), which are characterized by a full-gap bulk and robust gapless surface (edge)states, have gained much attention for their novel topological properties in recent years.[1–9]Several superconductors are considered to be unconventional and even topologically nontrivial, including Sr2RuO4[10–13]and heavy fermion compounds.[14–16]There are also theoretical proposals for artificially realizing the topological superconducting states by using thes-wave superconductor together with spin–orbit coupling (SOC). For instance, through the proximity effect ans-wave superconductor on a strong topological insulator becomes a spinlessp+ip-wave superconductor[1]or by applying a strong perpendicular magnetic field to ans-wave Rashba superconductor, topological superconducting states emerge.[17,18]However, there has been no definitive experimental evidence for the existence of TSCs so far,and it is still a grand challenge to provide valuable traces of them.

Transition metal dichalcogenides (TMDs) are a class of noncentrosymmetric layered van der Waals materials, which have been studied for decades as they usually exhibit superconductivity, charge-density wave state and other electronic phenomena.[19–24]Superconductivity in the bulk TMDs is usually conventional. However, in the ultra-thin films, a strong enhancement of the in-plane critical field indicates possible unconventional superconductivity caused by the large Ising SOC.[25–30]Several kinds of parity-mixed pairings, for instance, thes+f-wave andd+p-wave pairings, have been suggested as candidates for unconventional superconducting states in the monolayer TMDs.[31,33]

Here we study the pairing symmetry of the newly synthesized Janus TMDsMXY.[33–40]In a Janus TMD molecular layer,Matomic plane is sandwiched by two different atomic planesXandY.The stacking structure breaks the out-of-plane mirror symmetry, leading to a Rashba-type spin splitting of bands aroundΓpoint in the Brillouin zone (BZ). Previous works on the Janus layered TMDs mainly focused on their crystal, band structures and optical property,[41–44]while the nature of possible superconductivity has rarely been discussed.The parents of Janus TMDs,which have the 2H structure,are intrinsic Ising superconductors in most thin layer cases. We focus on the Janus TMDs with FS sheets centered around bothΓandK(K′)points based on the observation that the Rashba spin splitting occurs aroundΓ[36]while the Ising-type acts mainly on theK(K′) valleys.[45]The Cooper pairs are thus subjected to these two kinds of SOC effects. This type of FS topology provides an ideal platform for us to investigate the competition and interplay between these SOC effects on superconductivity. Naturally one could expect that the Rashba–Ising superconductivity leads to various kinds of mixed superconducting states in the Janus monolayer TMDs. As far as we know, the superconducting symmetry of H–MoS2monolayer coexisting with a gating-induced Rashba SOC has been theoretically studied by Yuanet al.in Ref. [31]. But since the FS of MoS2encloses only atK(K′)points,we believe the influence of Rashba SOC on Ising superconductivity is still not completely revealed.

In this work, we calculate the most favorable pairing states of the Janus monolayer with bothΓandK(K′) centered FS at different pairing interactions and chemical potentials by solving the linearized gap equation near the critical temperatureTc. We obtain a rich phase diagram which shows that at a relatively high chemical potential,a time-reversal invariant (TRI)s+f+p-wave pairing in irreducible representation (IR)A1of point groupC3vmay dominate the nearestneighbor(NN)pairing channels. Unlike the nodals+f-wave pairing in the monolayer H–MX2,[46]thes+f+p-wave has a large additional helicalp-wave component induced by the strong Rashba SOC, making the superconductor to be fullgap and topologically nontrivial, characterized by the invariant Z2= 1. At a lower chemical potential, a time-reversal symmetry breaking (TRB)d+p+f-wave pairing belonging to the two-dimensional IREappears, which can be a large-Chern-number chiral superconducting state with Chern number|C|=6 at appropriate pairing strengths. We emphasis that in the absence of Rashba SOC,a TRBd+p-wave pairing obtained from the same type of FS geometry always lead to a topologically trivial state,i.e.,C=0.

2. Model

The crystal structure of the Janus monolayer TMD is shown in Fig. 1(a). It can be viewed as a monolayer H–MX2whose top-layerXatoms are replaced by anotherYatoms,which breaks the out-of-plane mirror symmetry. The normalstate tight-binding Hamiltonian is constructed as follows:

andR4≡R1.ais the lattice constant,μis the chemical potential, andtandt1denote the NN and next NN hoppings, respectively.αkandβkare effective magnetic fields caused by Rashba and Ising SOC withαRandβsorepresenting corresponding strengths, respectively.We choose the value of parameters to be (t,t1,αR,βso) =(-0.06,-0.14,0.032,0.067)eV.The choice ofαRis referred toMXY(M= W, Mo andX,Y= S, Se, Te) in Ref. [36],whose Rashba splitting strength ranges from 77 meV·?A to 518 meV·?A,corresponding toαRvalue ranging from 0.015 eV to 0.10 eV in our lattice model by assuming the lattice constanta=3.3 ?A.[45]

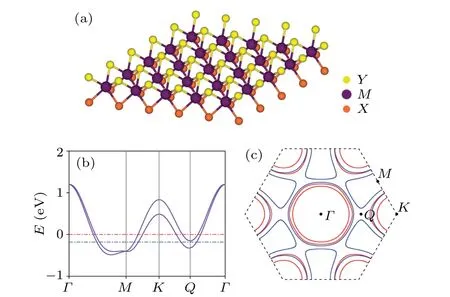
Fig. 1. (a) Crystal structure of a Janus monolayer H–MXY. (b) The constructed band structure of it. Fermi levels at μ =0 eV and -0.18 eV are denoted by the red and blue dashed lines,respectively,and their corresponding FS in the first Brillouin zone are presented in panel(c).

We set the chemical potentialμas an tunable parameter in our model. Whenμ=0 eV, this model is in analogy to the band structure of H–TaS2given by experiments and DFT calculations.[45,47,48]On the other hand, a chemical potentialμ=-0.18 eV will give an FS topology similar to H–TaSe2,which has dog-bone-shaped electron Fermi pockets centered atM.[49–51]The low-energy spectrum and FS of H–MXYfor the two chemical potentials,μ=0 eV and-0.18 eV,are simulated in Figs.1(b)and 1(c). In the figure of BZ,the“Q”point labels the position of van Hove singularity(vHS)corresponding to the first Lifshitz transition.One can infer from the figure that the first Lifshitz transition occurs aroundμ=-0.15 eV.

Table1. The classificationof basisgapfunctions basedonC3v symmetry. They are introducedas:C(k) = (1/)coski,C+(k)= ωi-1coski, S(k) = (1/3)sinki,S+(k)=(1/) ωi-1sinki,C-(k)=(k),S-(k()=(k)),withvectorx±=(x±iy)/2andphasefactor ω=exp-i2π/3.

Table1. The classificationof basisgapfunctions basedonC3v symmetry. They are introducedas:C(k) = (1/)coski,C+(k)= ωi-1coski, S(k) = (1/3)sinki,S+(k)=(1/) ωi-1sinki,C-(k)=(k),S-(k()=(k)),withvectorx±=(x±iy)/2andphasefactor ω=exp-i2π/3.

3. Symmetry analysis and method

The point-group symmetry of monolayer H–MXYis C3vand its basis gap functions are given in Table 1. Here we only consider the on-site and NN pairing channels.Depending on the spin angular momentum of the cooper pair,i.e., spinsinglet (S=0) or spin-triplet (S=1), gap functions take the matrix form as:

whereΔis the gap size value andcΓ,αdenotes the relative amplitude ofΔΓ,α(k), with the normalization condition∑Γ,α|cΓ,α|2=1. From Table 1 we have four classes ofkdependent basic gap structure:C(k) for the extendeds-wave pairing,S(k) for thef-wave type,C±(k) andS±(k) denote the chirald±idandp ?ip-wave types, respectively. Distributions of these gap structures in the momentum space are shown in Fig. 2. From Figs. 2(a) and 2(b) one can see that there is a nodal loop aroundΓpoint for the extendeds-wave pairing and nodal lines alongΓ–Mdirections for thef-wave.A pures-orf-wave superconductor then could be a nodal superconductor. On the contrary, thed+id- andp-ip-wave pairing gaps have finite nodes in the BZ and each node has its own chirality,as shown in Figs.2(c)and 2(d). Here we define the chirality by computing the phase winding of the gap function along a counterclockwise loop around the node. It can be easily obtained from the plots that the winding numbers of these nodal points are (wΓ,wK(K′))=(-2,1) ford+idand(wΓ,wK(K′),wM)=(1,1,-1)forp-ip. Obviously sum over the winding number of each node in the BZ gives zero. Superconductors of these two pairing forms are fully gapped and the winding number of superconducting gap on the FS is totally determined by the gap-function nodes enclosed by the FS sheets,which is also equivalent to the(first)Chern number.[46]

The intrinsic SOCs in our model destroy the inversion symmetry and give rise to admixture between singlet and triplet pairings. Lots of parity-mixed pairing states in the noncentrosymmetric superconductors have already been discussed in previous works.[52–57]Given that thedvector always tend to be paralleled to the SOC fields,e.g.,gk=αk+βkin our model, significant admixtures betweenψ,dxyanddzare expected in a Janus monolayer with both strong in-plane Rashba(αk)and out-of-plane Ising(βk)“magnetic fields”.

Fig. 2. Distribution of the gap structure (a) C(k) [extended s-wave], (b)S(k) [f-wave], (c)C+(k) [d+id-wave] and (d) S+(k) [p-ip-wave] in the momentum space. The hexagonal BZ is indicated by the gray box. The bright and dark areas in panels (a), (b) represent positive and negative values. The length and angle of arrows in panels(c),(d)respectively give the amplitude and phase of the complex C+(k), S+(k). Winding numbers of each gap node are given in the brackets.

wherev0,v1represent the on-site and NN pairing strengths respectively and the positive (negative) values of them denote attractive(repulsive)interactions.

4. Result and discussion

Our calculation allow us to construct an NN interactionchemical potential superconducting phase diagram as shown in Fig.3. The conventional on-sites-wave is more stable than NN one only if when on-site interaction is stronger than the NN one(v1/v0＜1),illustrated as bright blue regions in phase diagram. For the NN superconducting states in the rest of the phase diagram,the TRIs+f+p-wave pairing state(dark blue regions of the phase diagram), which corresponding to gap functions“ΨA1,nn+dA1,z+dA1,xy”,dominates the parameter space whereμ ＞-0.08 eV. By comparing to the monolayerMX2,whereA1phase is a nodals+f-wave pairing state,we conclude that it is the large Rashba SOC of Janus structure that induces helicalp-wave componentdA1,xyinMXY.Typical relative amplitudes of the three pairing components are (cA1,nn,cA1,z,cA1,xy)=(-0.24,0.91,-0.34). The helicalp-wave order parameter is stronger than the extendeds-wave on theΓ-centered FS, leading to a full-gaps+f+p-wave state with a nontrivial topological invariant Z2=1. The Z2number is calculated by using

moded by 2 where Pf[A] is the Pfaffian ofA.Θis the timereversal operator and|n,k〉is the eigenstate with an energyEn,kof the superconducting Hamiltonian.Cin Eq. (9) is the path enclosing half of the BZ,as shown in Ref.[58]. For topologically trivial(nontrivial)case,Z2=0(1). Figure 4(a)displays the enlarged-energy spectrum of the Z2=1 topological phase, whose topologically protected Majorana helical edge states are highlighted by the red color.

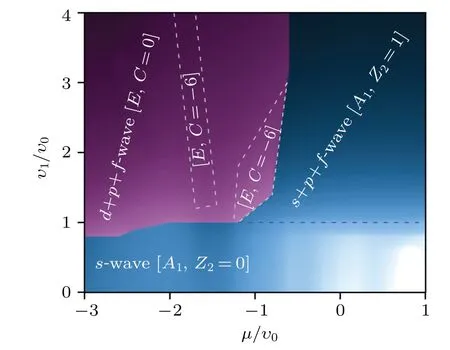
Fig.3. Superconducting phase diagram of Janus monolayer MXY in the v1–μ plane,with v0=0.1 eV.The blue and purple denote the A1 and E phases,respectively,and the dashed lines indicate the borders of topological phases.The critical temperature Tc exponentially increases from bright to dark,corresponding to a temperature range from 0 K to about 400 K. Topological invariant C(i=1)or Z2 of each phase is also illustrated.

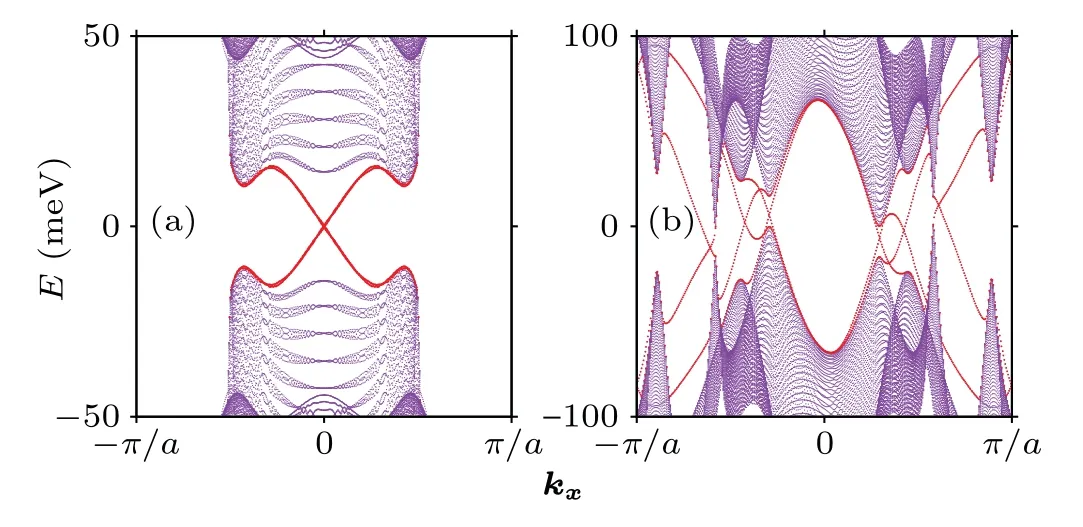
Fig.4.Energy spectra of the topological(a)TRI s+f+p-wave(A1,Z2=1)state, (b) TRB d+p+ f-wave (E,C=-6) state of the Janus monolayer,with open-boundary conditions along y direction. Gap sizes are enlarged for sight and the gapless edge states are highlighted by the red.

5. Conclusions

In this paper,the possible forms of pairing in Janus monolayer TMDs with FS centered around bothΓandK(K′)points have been investigated. Through analysis on the pairing symmetry and calculations based on the linearized gap equations,we have identified a Z2topologicals+f+p-wave superconducting state at the relatively high chemical potentials, and a chirald+p+f-wave state with a large Chern number|C|=6 when the chemical potential is lower. Unlike its parentMX2monolayers which are nodal or topologically trivial superconductors, our results show that Janus monolayer TMDs could be a promising candidate for the intrinsic helical and chiral TSCs.

Although we only focus on a specific model,the conclusions can be applied to all the superconducting Janus monolayer TMDs with strong-Rashba-splitting FS centered aroundΓ,e.g.,the group-V Janus H–MXY(M=Ta,Nb,etc.;X,Y=S, Se,etc.). There are superconducting conductance experiments observing zero bias conductance peak of the thin flakes of 2H–TaS2and 2H–TaSe2belowTc,[61,62]which indicates novel superconductivity in the atomic limit. Theoretical results suggest that these novel pairings could bes+f-wave andd+p-wave,[31,32,46]which both require a larger NN pairing attraction over on-site one in our framework. Consequently,it is most likely to realize thes+f+p-wave andd+p+f-wave topological states in Janus monolayer of group-V TMDs if the same assumption is taken for this family of materials.

Acknowledgements

We acknowledge Wei-Jian Li for useful discussions.Xian-Dong Li also thanks Ai-Lei He for helpful suggestions.Project supported by the National Natural Science Foundation of China(Grant No.11904155).