基于改進粒子群算法的恒力輸出器的力控制優化

王君, 任前程, 楊銘全, 汪泉, 曾順麒

(湖北工業大學機械工程學院，湖北武漢 430068)

0 前言

拋光和打磨等表面精加工在制造業中發揮著重要作用，這些操作不僅為了外表美觀，而且主要是為獲得指定的表面粗糙度。通常打磨拋光作業是由工人手動執行的，勞動成本高，效率低，工作環境惡劣且依賴于工人的技能熟練度[1-3]。因此，需要一種高效的打磨拋光方式代替手工打磨。工業機器人具有成本低、靈活性高、可編程性強和適合強度工作等優勢，因此工業機器人與打磨工藝相結合成為主要研究方向[4-5]。

在表面精加工應用情況下，控制接觸力以確保處理過的零件具有相同的質量至關重要。因此，工業機器人需要具有精確的力感知和力控制能力。很多學者對此問題進行了大量研究。FANAEI 和FARROKHI[6]在力/位混合控制的基礎上加上了模糊理論，將其應用到需要工具與零件之間保持恒定摩擦力的工況中。肖露和秦紅玲[7]為了解決加工過程中由于磨損造成的加工精度下降問題，提出了利用模糊控制與傳統PID控制相結合的方法控制系統輸出恒定的磨削力。黃婷等人[8]采用非線性PD控制，提高了被動柔順裝置的力/位混合控制精度。PEI等[9]通過結合反向傳播(BP)神經網絡和Smith 預測器的改進PID控制方法,縮短最大超調量和調整時間。

為提高力控制的控制性能，將粒子群算法引入到模糊PID控制中，并加入混沌策略對粒子群算法進行改進。利用MATLAB進行對比仿真分析，并在搭建的恒力打磨平臺進行實驗，驗證該方法的有效性。

1 恒力輸出器建模

1.1 恒力輸出器結構及工作原理

恒力輸出器模型如圖1所示。其工作原理：打磨拋光作業時，若打磨頭與待加工工件接觸產生的接觸力大于預設定的恒力值，出氣口打開，緩沖氣缸向上法蘭盤方向移動，直至接觸力等于預設定恒力。同樣，當接觸力小于設置的恒力時，進氣口打開，恒力輸出器的緩沖氣缸向下法蘭盤方向移動，直至接觸力等于預設定恒力。恒力輸出器內部還包含電子調壓閥、電磁閥、氣缸磁性開關。電子調壓閥的作用是控制緩沖氣缸內的氣壓，電磁閥控制緩沖氣缸的運動方向，氣缸磁性接近開關用于位置的監測，從而得到執行器末端的位置參數。

1.2 模型建立

1.2.1 受力平衡模型

圖2所示為恒力輸出器簡化的受力示意圖。

根據牛頓第二定律有：

(1)

式中:F為恒力輸出器的輸出力;f為活塞與氣缸的摩擦力;c為黏性阻尼；p0為緩沖氣缸上腔氣壓;A0為活塞的有效面積;x為緩沖氣缸的軸向位移;m為整體質量。

1.2.2 氣體流量模型

電子調壓閥的流量公式采用圣維南流量公式[10]表示：

(2)

式中:Ac為電子調壓閥的進氣閥口面積;pic為電子調壓閥進氣口壓力;poc為電子調壓閥出氣口壓力;T為絕對溫度；k為比熱容；R為理想氣體常數；Cf為流量系數。

根據式(2)可知流入調壓閥的氣體流量與進氣閥口開度有效面積有關。依據電氣比例閥的特點，閥口開度與調壓閥的控制電壓U有關，而電壓U會影響調壓閥出口的壓力poc，所以比例調壓閥的流量方程是關于輸入電壓U和比例調壓閥出口壓力poc的函數。則此氣體流量變化模型為

Δq=K1ΔU+K2Δpoc

(3)

氣體通過電子調壓閥后，需要通過長度為L的管道到達緩沖氣缸。忽略其他因素的影響，依據Anderson理論，得到式(4)，并根據式(4)得到緩沖氣缸氣體流量變換模型式(5)。

(4)

Δq=K3(Δpi-Δpo)

(5)

式中:pi為管道進氣端壓力;ρ為氣體密度;D為管道直徑；μ為氣體的黏性系數；A為管道橫截面處的有效面積。

假設進入緩沖氣缸中的氣體為理想氣體，氣體持續不斷地進入緩沖氣缸，并根據氣態方程(6)，可推導出緩沖氣缸上下兩腔的氣體流量qn關于氣缸內氣體質量變化率的方程(7)：

pinsideV=nRTo

(6)

(7)

式中:pinside為氣缸內氣體壓力;V為氣缸內氣體體積；n為氣體物質的量；To為進入緩沖氣缸后氣體溫度。

假設氣體隨著緩沖氣缸運動時不會和外部產生熱交換，則溫度初值Ts與運動過后的溫度To兩者關系能夠用式(8)表示，兩邊對時間求導得到式(9)并代入式(7)，由于整個緩沖氣缸在自身法線方向只存在微小的改變，為簡化模型,此方向可以忽略不計，更新后緩沖氣缸中的氣體質量與流量的模型為式(10):

(8)

(9)

(10)

1.3 恒力輸出器傳遞函數建立

將上面分析計算得到的式(3)(5)(10)進行拉普拉斯變換,分別得到式(11)(12)(13):

Q(s)=K1U(s)+K2Poc(s)

(11)

Q(s)=K3[Pi(s)-Po(s)]

(12)

(13)

由于氣體由比例閥的出口進入管道的入口，管道入口的壓力等于比例閥出口的壓力，即Poc=Pi。聯立式(11)—(13)可得

(14)

將恒力輸出器的受力方程(1)進行拉普拉斯變換得到式(15)，為簡化模型將摩擦力忽略不計。

ms2X(s)+csX(s)+F(s)=Po(s)Ao

(15)

連接在下法蘭盤末端的打磨工具與工件接觸時，由于反作用力的作用使得恒力輸出器產生x的移動，整體的等效剛度為K4，反作用力作拉普拉斯變換得到:

F(s)=K4X(s)

(16)

聯立式(15)和(16)得到:

(17)

將式(14)與式(17)相乘可得恒力輸出器的傳遞函數:

(18)

2 模糊PID控制系統

2.1 傳統PID控制結構

傳統PID控制器由比例(Proportional, P)、積分(Integral, I)和微分(Derivative, D)3個環節組成。PID控制算法對受控對象的傳遞函數的模型沒有特定的要求，只需要根據作業條件設定合適的比例、積分與微分的參數就能達到所需要的控制目標。

2.2 模糊PID控制結構

模糊PID控制主要由傳統PID控制器和模糊化模塊組成，其結構如圖3所示。根據實際要求，以系統反饋的壓力與給定值之間的偏差e和偏差變化率ec作為輸入，利用量化因子Ke與Kec將其轉換為模糊量，依據給定的模糊規則進行模糊推理，再通過模糊化的比例因子得到3個參數的變化量，與之前設定的PID參數進行合并，進而達到參數自整定的效果。

根據PID參數整定規則，得到自調整PID 3個參數的修正公式：

(19)

本文作者采用模糊PID控制設計了一種控制恒力輸出器的力的方法。依據模糊控制原理，將e和ec的模糊論域均定為 [-3,3],輸出的ΔKp的模糊論域為[-0.3,0.3]，ΔKi的模糊論域為[-0.06,0.06]，ΔKd的模糊論域為[-3,3]。根據模糊控制將上述5個模糊量的模糊子集均定為{NB, NM, NS, Z, PS, PM, PB}，e、ec、ΔKp、ΔKi、ΔKd的隸屬度函數全部選用三角隸屬度函數，隸屬度為[0， 1]。根據壓力偏差e與ec對ΔKp、ΔKi、ΔKd依次構建模糊規則，分別如表1—表3所示。

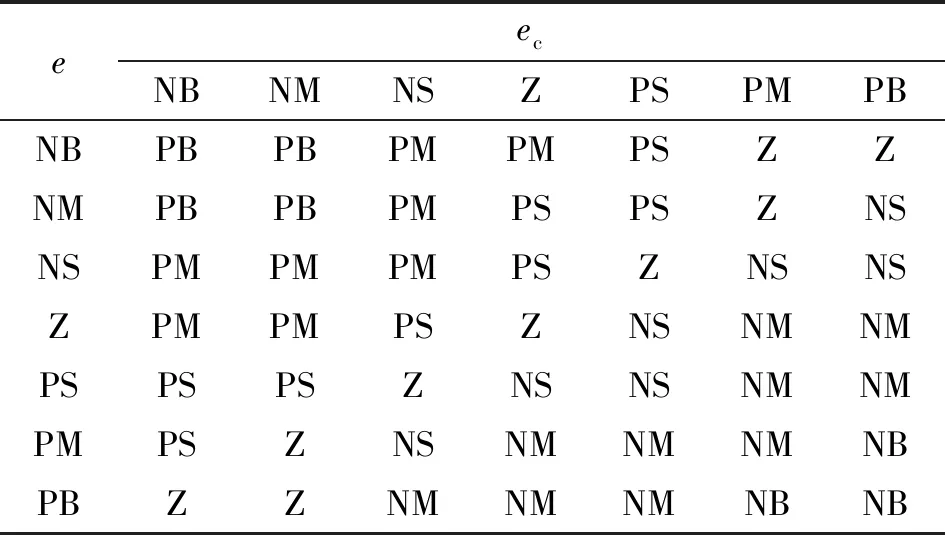
表1 ΔKp控制規則

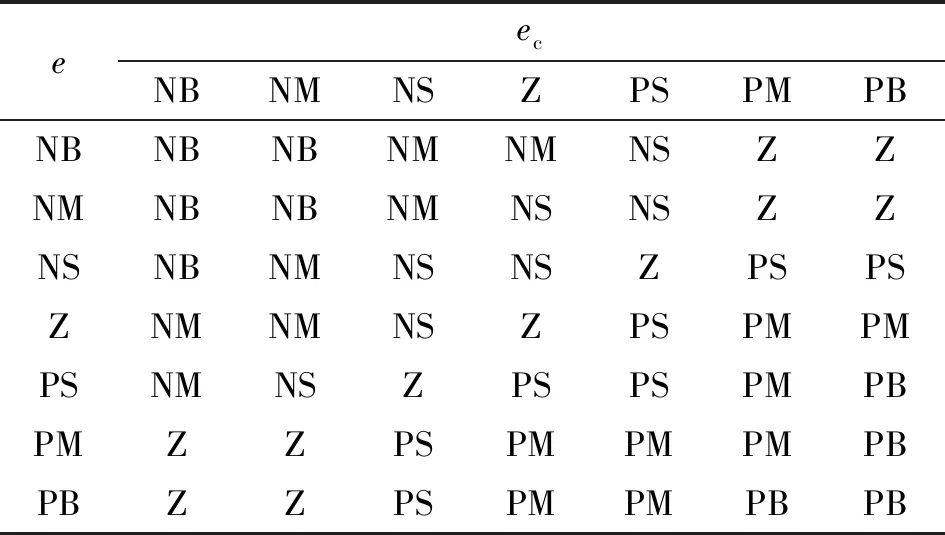
表2 ΔKi控制規則

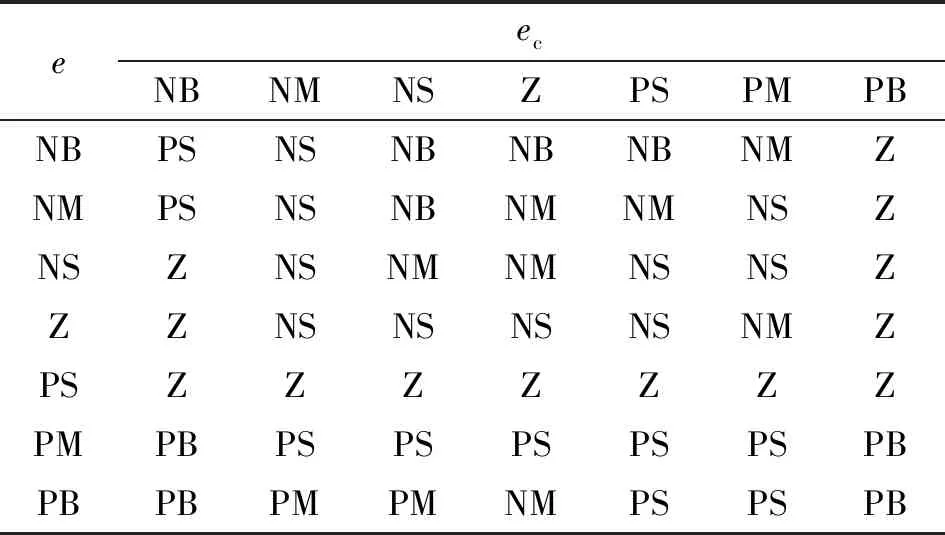
表3 ΔKd控制規則

3 粒子群優化PID控制

3.1 粒子群算法

粒子群優化算法(Particle Swarm Optimization，PSO)，是KENNEDY和EBERHART于1995年提出的，它源于對鳥群捕食行為的研究[11]。PSO因規則簡單、收斂速度快等特點，被眾多學者研究，并在PID控制參數優化整定中得到廣泛應用[12-13]。

假設在一個D維的目標搜索空間中，有N個粒子組成一個群落，其中第i個粒子的位置記為Xi=(xi1,xi2,…,xiD)，粒子速度記為vi=(vi1,vi2,…,viD)，搜索到的最優位置記為pBest,i=(pi1,pi2,…,piD)，整個粒子群搜索到的最優位置記為gBest=(pBest,1,…,pBest,i,…,pBest,D)，在找到這兩個最優值時，粒子根據式(20)和(21)來更新自己的速度和位置：

(20)

(21)

i=1,2,…,Nd=1,2,…,D

其中:ω稱為慣性權重;c1和c2為學習因子；r1和r2為[0,1]內的隨機數。

3.2 粒子群算法優化模糊PID

由于模糊PID中的量化因子和比例因子都為給定值，導致模糊PID系統自適應調參得到的不是最佳值，造成控制系統的局限性[14],所以引入粒子群優化算法對比例因子和量化因子進行優化。系統結構簡圖如圖4所示。

3.3 改進粒子群算法優化模糊PID

傳統的PSO算法比較容易陷入局部的最佳解，可以對慣性取值進行改進[15]，引出線性遞減權重:

(22)

式中:ωmax、ωmin分別為起始慣性權重與終止慣性權重；t為當前迭代次數；tmax為整個迭代過程中最大迭代次數。此方法能夠滿足慣性權重為動態變化過程，但是在算法優化的過程中慣性權重的變化率并未變化。為使慣性權重擁有動態的速度變化率，在線性慣性權重遞減中加入混沌系數，使得慣性權重在線性遞減時盡可能在曲線的下方發生振蕩，慣性權重變化速率不再是固定的，進而增強全局搜尋能力。

ft=μft-1(1-ft-1)

(23)

混沌線性慣性權重遞減系數為

ωnew=ωtft

(24)

式中：ft為第t次迭代的混沌值；μ為混沌系數。

將ωmax=0.9、ωmin=0.1、μ=4、起始混沌值f0=0.63代入式(22)、(23)和(24)，并根據所得數據繪制出圖5。可知：混沌遞減系數在保證總體的慣性系數不斷減小的同時能在較小范圍內振蕩，避免了算法陷入局部最優。

采用改進粒子群優化模糊PID控制參數時，每個參數之間相互影響，要求所有指標都達到最佳是不可能的，故需要一個確定誤差是否最小的評價性能指標。引入性能指標函數ITAE作為恒力輸出器控制系統性能評價指，其表達式為

(25)

基于圖4，設計改進粒子群算法優化PID控制流程，如圖6所示。

4 仿真與實驗分析

4.1 仿真分析

改進粒子群優化模糊PID參數設置：種群規模N=10，粒子維度D=5，學習因子c1=c2=1。5個粒子的速度的最大值均為1、最小值為-1；5個粒子的最小位置矩陣為[1.29，1.29，2.75，0.35，0.85]、最大位置矩陣為[1.68，1.68，3.25，0.66，1.03]。 PID 3個參數為Kp=4.978、Ki=0.001、Kd=1。

將上述參數代入模糊PID控制器，則系統中采用未優化的模糊PID控制和文中提出的基于改進粒子群算法優化模糊PID控制下的階躍響應能力如圖7所示。

由圖7可知：經過改進粒子群算法優化的模糊PID控制系統比模糊PID控制系統更快達到目標值，收斂速度更快，超調量也明顯降低，整體的超調量為8.91%，在1.3 s達到穩定。

4.2 實驗分析

使用基于恒力輸出器打磨機器人對打磨對象進行打磨時，首先考慮的因素是打磨頭與打磨對象之間的接觸力。恒力輸出器的輸出力是否穩定決定加工件表面粗糙度是否均勻。由于在系統進行打磨拋光的過程中，末端的恒力輸出器與打磨頭可能會隨著零件的輪廓改變自身位姿。為確保在該點的法線方向輸出拋磨力，根據圖8所示的受力分析圖構建受力方程(26)。其中，m1為打磨頭的質量；Fs為接觸力。

Fs=p0A0-f+m1g

(26)

式(26)為恒力輸出器與打磨工具處于垂直方向的受力方程，若零件屬于曲面類零件，則在任意一點進行打磨拋光時恒力輸出器與打磨工具這個整體與垂直方向成θ角，則受力方程為式(27)：

Fs=p0A0-f+m1gcosθ

(27)

忽略氣缸與活塞摩擦力，可得簡化后的恒力輸出器的輸出力公式：

F=Fs-m1gcosθ

(28)

4.2.1 恒定輸出力實驗

實驗采用氣袋作為被擠壓對象是因為氣袋中含有足量的氣壓，若輸出力過大或大幅度變化對其進行擠壓，則氣袋容易爆裂。實驗中保證恒力輸出器垂直擠壓氣袋，如圖9所示。分別采用模糊PID控制方法和改進粒子群算法優化PID控制方法，采集到2種控制方法的輸出力變化數據，并繪制輸出力變化圖，分別如圖10、圖11所示。

整個實驗過程中氣袋未發生破裂。觀察圖10與圖11能夠得出整個實驗過程中基于粒子群改進算法優化的模糊PID控制的拋磨力相對模糊PID控制的輸出力變化幅度更小且更加穩定，力跟蹤效果較好。

4.2.2 正弦輸出力跟隨實驗

由式(28)可知，恒力輸出器的輸出力與三角函數相關。為監測在2種控制方法下輸出力的跟隨狀態，設計正弦力跟隨實驗。將正弦力的振幅設置為10 N，偏距設置為20 N，頻率為0.4 Hz，同樣采取上述2種控制方法，并將采集到的正弦力變化數據繪出圖，分別如圖12、13所示。由圖12可知：兩者的力跟隨性都較好，且誤差相差不大，均在1 N以內，但是改進粒子群優化的模糊PID控制的響應速度更快。表明在誤差允許范圍內，改進粒子群算法優化的模糊PID控制的恒力輸出器擁有更快的響應速度。

4.2.3 打磨拋光實驗

以40 cm×23 cm鋁薄板為實驗對象，并采用改進粒子群算法優化模糊PID控制系統控制恒力輸出器進行打磨實驗，如圖14所示。輸出力設置為10 N，對鋁板進行打磨，同時采集打磨過程中實際拋磨力的大小，并將數據繪制成折線圖，如圖15所示。可知:實際的拋磨力誤差能夠保持在±0.3 N內。

5 結論

針對模糊控制中的量化和比例因子均為固定值、造成控制系統局限性的缺點，提出一種基于改進粒子群算法優化的模糊控制，不斷迭代尋優出最佳的量化和比例因子。結果表明：經過改進粒子群算法優化的模糊PID控制系統超調量更低、響應速度更快、收斂速度更快、恒力輸出器輸出力變化幅度更小且更加穩定，驗證了改進粒子群算法優化模糊PID控制策略的有效性。