立式復合磨床可靠性仿真分析評價
陳澤眾,林志偉,傅建中
(浙江大學機械工程學院,浙江杭州 310000)
0 前言
高精度復合磨床作為機床產品中尤為重要的一員,是我國工業產品、制造系統及航空航天等重要領域實現生產現代化的重要手段[1],是實現工業產品高精度加工的重要途徑,融合了許多學科和技術領域最新的研究成果,是許多國家重要工業儲備的基本要素[2]。目前,國產數控磨床在可靠性方面與國外產品相比還存在差距,數控裝備的高端市場仍然被其他發達國家如德國、日本所生產的產品占據,在加工精度、設備加工速度、工藝種類、數控系統穩定性等方面與國外數控加工設備相比仍有很大差距。以平均無故障間隔時間(Mean Time Between Failures,MTBF)為例,國產設備與進口設備在這一技術指標上仍存在上百小時的差距。而產生差距的原因中,對可靠性問題的研究不足是主要原因之一,已經成為阻礙我國高端數控設備技術革新的關鍵障礙[3]。數控系統的可靠性是關系到數控系統性能的一個重要指標。磨床作為數控裝備中的重要產品,應著重注意設計與研發過程中的可靠性分析與設計,其可靠性與精度保持技術對正確評價產品性能、提高產品質量具有重要意義。
1 可靠性設計概述
可靠性設計貫穿產品研發的始終,在不同的階段發揮不同的作用,因此應建立面向并行工程的數控磨床可靠性控制模型[4]。通過對磨床產品研發全周期進行可靠性設計和分析,可以盡可能地減少設計制造中的不足和缺陷,對提高數控磨床的綜合性能起到了顯著的作用。
1.1 概念與定義
在對數控磨床進行可靠性設計與分析優化時,主要參考以下4個技術指標:平均無故障間隔時間、平均修復時間、固有可用度、平均壽命[5]。
平均無故障間隔時間MTBF是指對于具備修復條件的數控設備,相鄰兩次故障發生的平均值是衡量可靠性的重要指標,具體數值在產品標準中給出。
平均修復時間(Mean Time To Repair,MTTR)又稱平均故障維修時間,是指從監控端發現故障到磨床系統恢復原有正常運轉狀態所需間隔時間的平均值,包括確認失效發生消耗的時間、設備維修消耗的時間、尋找并獲取替代配件消耗的時間、維修團隊響應時間、記錄任務時間及設備重新啟動的時間[6]。該時間不僅和產品本身的設計、制造水平有關系,而且和實際工況時使用的方法的科學性、維修的技術水平、備件的存儲策略息息相關。
固有可用度(Availability)A,又稱有效度,是在默認的運行工況下,磨床系統和其零部件保持預期額定運轉時具備正常功能的概率。這個指標是評價數控設備實際利用率的一項重要依據,也是直接影響數控系統生產能力的重要因素[7-9]。
平均壽命(Mean Time to Failure,MTTF)指一定數量的數控設備從正式交付使用到最終不可修復徹底失效這段有效運轉時間的平均值[10]。
表1所示為機械裝備常用的可靠性影響因子及影響程度分布列表。作為常用的數控加工設備,復合磨床應按照此規范進行可靠性的設計和評估。設計技術對設備可靠性的影響最為明顯。合理的設計將大大減小磨床在后期帶載荷試驗中出現故障的概率[11]。

表1 數控設備可靠性影響因子分布
1.2 設計與開發
以磨床實際結構為入手點,對具體的零件、組分、系統進行獨立的可靠性分析設計,再將獨立組分的可靠性分析結果進行加權,得到床身總體的可靠性評價指標[6]。例如,一個數控系統有K個組成成分,各個組成成分間的可靠性互相獨立是最簡單的可靠性相關性。這種情況下的磨床設備可靠性表達式為
q=q1×q2×q3×…×qK
(1)
第i組成分的不可靠性為Pi=1-qi,則系統的不可靠性為
P=1-p=1-(1-P1)(1-P2)…(1-PK)≈
P1+P2+…+PK
(2)
圖1所示為MGKF1800型復合磨床的結構簡圖。MGKF1800型高精高效立式復合磨床主要由底座、導軌架、進給系統、滑枕系統組成。加工工件時,左、右2個砂輪同時工作,對固定于靜壓工作臺的毛坯件進行磨削。2個砂輪系統可以獨立運行,也可以相互協作進行加工。砂輪的橫向和縱向均配置了滾珠絲杠結構,以實現砂輪的橫向和縱向進給;利用數控系統的控制完成磨削路徑的規劃和進給運動。其中,進給系統和內嵌式滑枕是磨床設備的2個主要組成部分,直接影響其加工精度,包含電機、絲杠、軸承等易產生故障的零部件。為保證磨床運行的可靠性,在零件選型時應綜合考慮上述零部件的材料構成、功率選型、平均壽命、保養周期,提升磨床的固有可靠性。
1.3 故障樹法分析
故障樹法(Fault Tree Analysis,FTA方法)是由頂事件(不希望發生的事件,如數控磨床異常發熱,精度下降等)和構成它的全部底事件按邏輯關系連接而成的[12]。在利用FTA方法解決工程問題時,一般采用上行法從上至下求解頂事件與底事件的邏輯關系,建立頂事件邏輯關系表達式,再采用冪等律和吸收律分別去掉重復事件和多余的項,確定故障樹的最小割集,從而找出影響數控磨床正常工作的各失效因素及其邏輯關系,明確磨床的可靠性薄弱環節,即磨床的關鍵元器件和核心零部件。針對磨床的可靠性薄弱環節,提出改進措施并反饋給設計部門進行產品改進,提高產品的固有可靠性。可以通過建立邊界條件更好地利用故障樹解決磨床中可能出現的問題。
建立邊界條件能有效地簡化故障樹的多余部分,同時提高故障樹的分析效率。主要的邊界條件有:禁止出現事件、不可能發生事件、必然事件、初始狀態。建立邊界條件時應注意以下幾點:
(1)小概率事件與細微零部件的故障和小故障事件不能視為同一事件;
(2)有的故障發生概率雖小,但一旦發生則后果嚴重,為安全起見,這種小概率故障就不能忽略;
(3)故障定義必須明確,避免多義性,以免使故障樹邏輯混亂[13]。
圖2所示為故障樹分析法的流程簡圖。故障樹分析的基本原理是選取某一個對整機系統影響最大的零部件所產生的故障作為建立系統故障關系的頂事件,然后將產生這個故障的誘發因素逐級拆解為不同零部件產生的故障的中間事件,最終分解到最基礎零部件的故障事件為止,從而得到樹狀的故障邏輯關系圖。
在建立故障樹過程中,可根據磨床自身的實際組成結構增加或刪除子系統[14]。在磨床中,主軸系統最為關鍵,因此在建立故障樹時,可以把磨削主軸的工作狀態作為頂事件,軸承、滾珠絲杠、導軌等依次作為底事件進行分析。磨床加工過程中產生故障的2個最主要的原因是散熱效率和應力集中,過高的應力和散熱不均都會導致床體零部件的故障出現。因此,力和熱的傳導路徑可以作為構建故障樹的一條首選路徑,即從磨削砂輪出發,經主軸,軸承傳至機架末端,便于在后期的試運行中與檢測數據更好匹配,提高故障檢測及修復的效率[15-16]。
2 工況模擬分析
針對磨床系統的可靠性分析可以依靠仿真方法對磨床工作性能進行初步評價,從而判定磨床機構的設計薄弱點,進而進行改進和升級。在考慮磨床典型結合面的基礎上,通過在SolidWorks中對數控磨床整機模型進行簡化,將去除復雜無用特征的建模導入ANSYS Workbench中進行整機的穩態、瞬態熱分析和熱-固耦合分析,根據該分析結果識別出MGKF1800型立式磨床設計過程中的薄弱環節并對此提出優化策略,從而為提高該磨床的靜動態性能提出合理的建議,指導其設計定型。
2.1 模型預處理
在進行整機設計建模時,為保證其機械結構的合理性及制造加工的直觀性,應把磨床的全部細節進行完整建模。但在對磨床結構進行有限元分析時,由于網格劃分的特點和節點的分布特點,導致一些細小的結構并不能獲得合適的網格劃分,同時,一些實際制造裝配中的接觸在有限元仿真中同樣不能進行網格劃分,例如緊定螺釘的點接觸,磨床殼體間的過盈配合等。因此,將磨床整機三維模型導入有限元軟件之前,為免去一些不必要的計算量,需要對該模型的某些結構進行簡化[17]。例如,某些局部零件的倒角、小孔、螺釘等不利于網格劃分的結構均可以忽略。在簡化過程中,保留必要的孔、梁、肋板結構。模型預處理及網格劃分如圖3所示。各部件材料如表2所示。
各主要材料的屬性如表3所示。
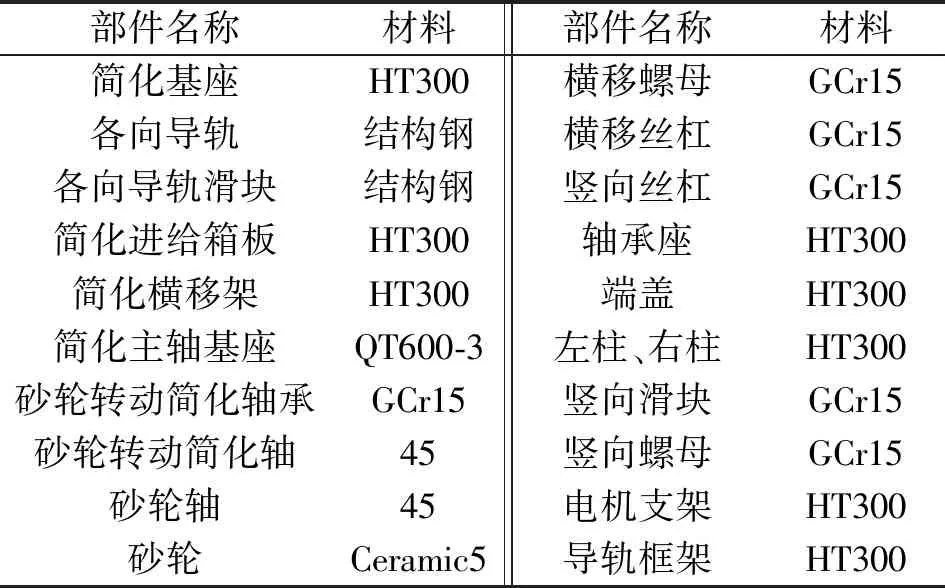
表2 整機零部件材料
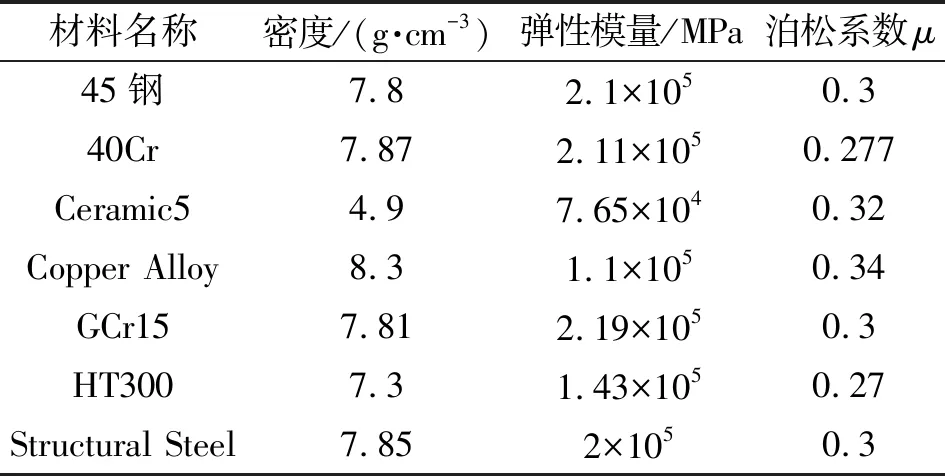
表3 各部分材料屬性
2.2 結合面選取
在磨床系統中,各個零部件絕大多數都是通過面間接觸實現裝配關系的,如支撐柱、摩擦副、導軌、軸承座等。其中,根據接觸面是否運動及運動的種類不同可細分為固定結合面、半固定結合面、運動結合面。固定結合面通常出現在承力結構,即在加工中保持相對靜止狀態的結合面,如底座與支撐柱間、電機與機架間等。半固定結合面是指接觸情況隨時間及工況不斷變化的結合面,如車輛制動盤的分離和接觸。運動結合面則為參與磨床系統加工的長時間具有相對運動的結合面,如軸承系統、絲杠螺母副、滑動導軌副、滾動導軌副等。
2.3 熱、固及耦合分析
有限元分析過程中需要定義其邊界條件,主要包括約束邊界和載荷邊界[18]。針對磨床運行時的靜態特性、動態特性及模態特性等不同仿真過程,約束和載荷的施加有所不同。根據整機零部件參數計算獲取邊界條件后,針對立式磨床進行熱、固分析及耦合分析,測定整機的實際加工可靠性。
圖4所示為仿真分析過程中引入的復合磨床熱邊界條件示意圖。其中,邊界條件主要分為兩個方面:
(1)熱源部件。例如軸承、電機、絲杠、滑塊等在實際加工中都會因設備的運轉自發的產生熱量,因此把這些部件設置為熱源;
(2)散熱部件。如基座、支撐柱、軸承座、框架等在實際加工中不會自主產生熱源,而是作為傳熱的中間階段,因此將這些部件的外表面設置為熱對流面。
圖5所示為典型數控磨床正常運行時的溫度-時間曲線。可以看出:磨床啟動后溫度上升較快,一段時間后,溫升速度減慢,最終溫度上升到平衡溫度T后達到一個相對穩定的狀態。從設備啟動溫度開始上升到溫度平衡的這段時間稱為預熱階段。當數控磨床的整機溫度達到運行穩定溫度后,溫度場達到穩態,其熱變形也趨于穩定。穩定的溫度場所引起的加工誤差是有規律的、可預測的[19-20]。因此,應在數控磨床運轉到熱平衡后再進行零部件加工。一般由于溫度分層變化,床身表面高于床身底面,形成溫差使床身彎曲變形,導致加工誤差。一些加工大型工件的龍門銑床等,由于其某個方向的進給范圍要求較大,該方向的導軌及床身長度較大,一旦受熱,易產生更大的彎曲變形[21-22]。假定一個龍門銑床的床身長度L=6 400 m、高H=600 mm,溫差Δt=1 ℃,鑄鐵線膨脹系數a=11×10-6℃-1,則床身的變形量為
Δ=(a×Δt×L2)/(8×H)=[11×10-6×1×
(6 400)2]/(8×600)=0.093 9 mm
(3)
由此可以看出,床身導軌的直線進給精度會受到直接影響。
2.4 仿真結果分析
設置好約束和載荷后,可對整機進行熱分析及應力分析,借助熱-固耦合分析結果評價磨床整機的加工可靠性[23-25]。
2.4.1 熱仿真結果分析
由于磨床結構復雜,為更加清晰地展示磨床的溫度分布,將溫度最大值附近的零部件進行拆分,得到的溫度分布如圖6所示。
由圖6可以看出:溫度最大值的位置在橫移平臺的絲杠螺母處,溫度為48.961 ℃。以穩態熱溫度場的邊界條件對磨床系統進行瞬態熱分析,以300 s為采樣間隔,針對12 000 s內磨床的溫度場變化進行仿真分析,得到整機的40組溫度數據。在數據處理的過程中,簡化溫升不明顯的次要部件,如底座、外殼、支架等結構件。磨床系統中主要發熱部件的溫度場數據整理結果如圖7所示。
由圖7可知:(1)溫度較高的部件還包括橫向進給和縱向進給絲杠的軸承、滾珠絲杠及主軸部件;(2)除去電源及熱源部件,整機部件溫升較小,都在10 ℃左右。對所得數據進行整理,得到時間-最值溫度關系如圖8所示。
由圖8可知:當磨床運行到12 000 s時,溫度曲線上升速度明顯減慢,趨于平衡,因此12 000 s可近似視為該磨床的預熱時間。穩態溫度場是在初始溫度(20 ℃)下分析得到的,瞬態溫度場環境溫度默認為常值。由圖8還可知:磨床最高溫度達到46.186 ℃,最大溫升23.563 ℃,最高溫度點出現在橫向進給絲杠螺母處。分析圖7、圖8可得到以下結論:
(1)從分析結果來看,復合磨床各部分經過3 h左右,溫度基本達到穩定,可見磨床整體達到熱平衡的時間較長;
(2)磨床最大溫升約為30 ℃,多發生在熱源附近,而磨床床身的溫升較小;主軸處的溫升約為15 ℃,可見由于主軸基座默認為主動散熱結構,較好地控制了主軸的溫度;另外,由于絲杠螺母、軸承處發熱較大,且缺乏主動散熱方式,散熱不暢導致溫升較大;
(3)磨床開機1.5 h內溫度變化較快,尤其在各個熱源處溫度上升極快,由此得磨床應進行適當的預熱,但從分析結果看,單純預熱主軸并不合理,熱機時對于其他熱源也應該適當考慮。
2.4.2 熱-固耦合仿真結果分析
在獲得穩態及瞬態的溫度場分布仿真結果后,將溫度場作為中間輸入值輸入至磨床的結構建模中,作為初始條件對整機的瞬態熱變形進行分析和計算,結果如圖9所示。
由圖9可知:(1)磨床整機的瞬時最大熱變形達到0.73 mm,最大熱變形點的位置聚集在橫向進給滾珠絲杠附近;(2)熱變形較大的部件還包括縱向進給滾珠絲杠、各個驅動系統的軸承處以及旋轉工作臺內部的蝸輪蝸桿處等;(3)整機的熱變形瞬時最大值在6 000 s出現,且其他幾個時間點也出現了熱變形的最值突變,原因可能是瞬態熱變形仿真計算的是近似解,在網格劃分后會產生一定程度的誤差,導致最值點沒有出現在最終時間點,因此應將這4個誤差點作為異常數據,觀察其余數據的擬合趨勢。可以看到,在磨床運行2 h左右時,熱變形最值基本穩定。
分析圖9中瞬態熱變形最大及最小的兩條曲線,可得到以下結論:
(1)除去仿真中出現的誤差點,整機的熱變形均保持在0.2 mm以內,由此可見此復合磨床的熱結構比較穩定,熱變形較小;同時,隨時間推移,磨床的熱變形達到平衡,且所需平衡時間在2 h內,在合理范圍內;
(2)橫向進給和豎向進給的絲杠系統均有較為明顯的變形,原因是絲杠作為桿狀結構,發生熱伸長后由于兩端固定,會導致比較大的熱變形,同時兩端的支撐軸承也相應地出現了較大的變形。
圖10所示為熱變形最大處的放大圖。可知:由于絲杠兩端由軸承進行軸向和徑向的固定,當絲杠溫度升高時,其向絲杠軸線外側膨脹,為橫向進給帶來誤差。
3 試運行及數據收集
這個階段的可靠性工作重點是保持數控磨床的固有可靠性水平,通常會針對新型磨床試制產品進行早期故障試驗。數控磨床完成生產裝配后,須經過人工調試、空轉測試與加工精度預檢,同時必須用包含數控磨床常用功能在內的數控程序進行不加工零部件的連續空轉試驗,該試驗的基礎時長為72 h[26]。借助該方法確定由于設計、工藝、制造和裝配等原因引起的故障。前文提到,橫移絲杠為磨床運轉中的最薄弱環節。因此,應在絲杠附近布置溫度傳感器,收集絲杠的溫升變化,判斷絲杠是否在加工過程中可以始終保持在材料的可靠性能范圍之內。
此外,可以通過收集與分析磨床試運行中獲得的數據,改進現有的結構及運行方式。及時收集與分析該階段的可靠性數據有助于發現影響數控磨床可靠性設計、制造和裝配中的不利因素,以便采取措施減少損失。在可靠性評價中,最重要的也是最基礎的工作是對可靠性數據進行統計處理和分析,判定分布力,估算系統的可靠性分布參數、使用壽命等概率分布,為磨床的可靠性計算奠定基礎[27]。可靠性分析中最常用的概率分布有均勻分布、正態分布、χ2分布、威布爾分布、指數分布等。在這些分布中,有的在概率論中早已提出作為一般的基本分布,而后才在可靠性技術中被采用;有的則是在可靠性研究中,從某種物理背景出發推導出來的分布。根據磨床的技術特點,計劃采用威布爾分布對數據進行處理和計算。該分布函數因為含有2個或3個參數,比其他分布類型適應能力強,對磨床運行溫升曲線的3個失效期都可以適應,對不同種類、不同學科的試驗數據擬合的能力和效果都較好。復合威布爾分布廣泛應用于各個行業,如紡織、醫藥、化工、生物、冶金、機械、電工電子、航空等領域。威布爾分布密度函數為
γ≤t,0 (4) 其中:m表示形狀特征;η表示尺寸特征;γ表示位置特征。當m=1時為兩參數指數分布密度函數。因此,指數分布是威布爾分布的特殊形式。當m=2時稱為瑞利(Rayleigh)分布。m的數值不同,威布爾分布的密度函數圖像形狀也有所變化。位置參數γ是指產品出廠正常使用至失效的時間,因此也稱為最小保證壽命。但是在實際工況下,為保證磨床的可靠性,常取γ為0。此時,式(4)可化為 (5) 稱式(5)為兩參數威布爾分布密度函數。 威布爾分布函數為 (6) 兩參數威布爾分布有如下性質: 威布爾分布的期望和方差分別為 (7) (8) 可靠度為 R(t)=1-FW(t;m,η)=e-(t/η)m (9) 失效率為 (10) 平均失效率為 (11) 可靠度壽命為 (12) 中位壽命為 t(0.5)=η(ln0.2)1/m (13) 當R=e-1時,得到特征壽命為 t(e-1)=η (14) 獲得磨床的故障數據后,可根據公式(14)進行擬合,獲得磨床的可靠性參數,用來分析磨床的設計及工作情況是否符合可靠性準則并針對設備的薄弱環節進行升級和改進。 本文作者借助數控產品的可靠性基本原理及FTA方法對雙頭立式磨床的設計可靠性進行初步評判,分析其設計的合理性。經過模擬工況下的熱分析及熱-固耦合分析,得到磨床系統的熱溫度場最大點及熱變形最大值發生點集中于滾珠絲杠副處。在磨床產品投入量產后應注意如滾珠絲杠副等被動散熱效果差的節點,可加入液冷或風冷等主動散熱方式,保證磨床的綜合散熱效果。在調試與加工階段,應廣泛收集磨床各個關鍵節點的溫度場及熱變形場數據,并根據數據評估磨床的預期使用壽命及精度等級。進給系統的運行質量是保證加工精度的重要一環,因此在磨床試制及試運行時應著重考慮此處,以達到預期的設計要求。當前可靠性分析中,模擬工況仿真的準確性和精度尚不能完全替代實際試運行,因此應將模擬仿真與實際加工相結合,才能更好地提高磨床產品可靠性設計優化的效率和質量。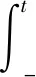
4 結語

