韋達定理：歷史、教育價值及啟示

黃賢明 (江蘇省蘇州高新區景山實驗初級中學校 215129)

韋達定理是一元n次方程根與系數關系的定理，本文主要討論一元二次方程的情況．在現行教材中，韋達定理一般編排在一元二次方程的解法之后，在中學階段具有較為廣泛的應用價值．《義務教育數學課程標準(2011年版)》中韋達定理為選學內容，《義務教育數學課程標準(2022年版)》(下稱新課標)則將韋達定理重設為考試內容，說明韋達定理的教育價值不容忽視．研究韋達定理的起源與發展，不難發現其蘊藏著深厚的歷史底蘊，是HPM教學研究的重要素材；同時韋達定理作為數學定理，在其發現、探索、證明、應用等環節中也涉及到數學抽象、邏輯推理等素養的 培養．因此，本文從歷史和教育價值兩個方面透析了韋達定理，以期提出韋達定理教學的建議與啟示．

1 韋達定理的歷史

1.1 韋達定理的起源與發展

韋達定理從起源、發現、完善、證明到推廣歷經了數百年，歷史上對于方程的根與系數關系的探索可以追溯到16世紀，意大利數學家卡丹 (G.Cardano,1501—1576)、法國數學家佩勒蒂耶(J.Peletier,1517—1582)、意大利數學家邦貝利(R.Bombelli,1526—1572)都發現了方程的根與系數的規律[1]．1615年，法國數學家韋達(F.Vieta,1540—1603)在《方程的理解與修正》一書中給出了形如-x2+px=q(p,q>0)的方程的兩根之和為p，兩根之積為q，但韋達并沒有考慮重根和負根的情況．1629年荷蘭數學家吉拉爾(A.Girard,1595—1632)在《代數新發明》中討論了一般n次方程的根與系數關系，并將根推廣到負數、虛數，且發現了方程根的“冪和公式”．直到18世紀，瑞士數學家歐拉(L.Euler,1707—1783)、法國數學家拉克洛瓦(S.F.Lacroix,1765—1843)等人才給出了韋達定理的嚴格證明[2]．在19世紀蘇格蘭數學家華里斯(W.Wallace,1768—1842)利用韋達定理得到一元二次方程的求根公式[3]．由韋達定理的歷史可以看出，求根公式的出現遠晚于韋達定理，并非教科書所編排的順序，其次早期韋達定理考慮的是二次項系數為1的一元二次方程．

1.2 韋達定理的證明

縱觀韋達定理的歷史發展，許多數學家都為定理的證明作出了貢獻，并且他們的證明思想都圍繞著設而不求的數學思想．

(1)韋達代入相減法．

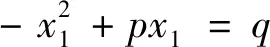
在證明中，韋達并沒有考慮到重根的情況，但他是最早以定理的形式探究方程的根與系數關系的數學家，并且在他的證明過程中也蘊藏著設而不求的數學思想與代入相減的數學方法．

(2)吉拉爾代入相減法．

數學家吉拉爾的證明是站在韋達的“肩膀”上，證明思想與方法都類似于韋達的證明．但該證明彌補了對重根情況的討論，且韋達定理的形式也與如今教材中所呈現的相同．

(3)歐拉因式分解法．

設方程x2+px+q=0的兩根為x1和x2，則原方程可化為(x-x1)(x-x2)=0，即x2+px+q=x2-(x1+x2)x+x1x2，比較系數，得x1+x2=-p，x1x2=q．

歐拉的證明也是采用設而不求的數學思想，但與韋達證明的不同就是利用所設兩根對方程進行因式分解，比較系數得到定理，這也是人教版教材中所采用的證明方法．

(4)拉克洛瓦“新證法”．

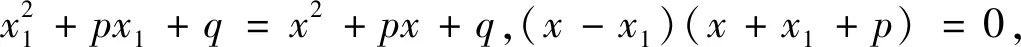
拉克洛瓦在證明中沒有將兩根全部設出，通過只設一根的方式，讓另一根通過運算推理獲得．

2 韋達定理的教育價值

2.1 串聯中學解題的重要法寶

在初中階段，韋達定理并沒有得到較為深入的探究與應用，其主要用于解決判斷方程根的符號這類問題．此外，從課外拓展的視角下，韋達定理還可以用于求解特殊的方程組、分式方程、不定方程等問題[4]．在高中階段，韋達定理在解析幾何的求解中較為常見，尤其是涉及直線與圓錐曲線的關系問題，借助韋達定理可以巧妙地設而不求、簡化運算．在韋達定理的證明方法中，利用因式分解法可以將一元二次方程推廣到一元n次方程，走向定理的一般化．因此，韋達定理在中學數學解題中，其內容、思想、方法都是學生的重要法寶．

2.2 發展核心素養的重要載體

新課改以來，數學核心素養與數學思想方法受到一線教師的重點關注．韋達定理作為數學定理，其本身就具備較強的嚴謹性和邏輯性．在教學實踐中，不同的教學設計下，韋達定理能夠達到不同的培養目標．以蘇科版教材的設計為例，在觀察、比較具體方程及其根的關系的活動中，有利于培養學生數學抽象素養與合情推理能力；在使用求根公式證明定理環節，有利于培養學生數學運算和邏輯推理素養．除了教材的設計，教師還能從不同的視角對韋達定理的教學進行再設計．例如，基于5E教學模式并融合了因式分解法證明韋達定理、利用韋達定理證明求根公式等活動，讓邏輯推理素養串聯起整個課堂[5]．再如，在發現規律環節中設計“數學趣味游戲”，讓學生根據已給方程的根構造一元二次方程，并得出猜想，該環節側重于學生數學抽象素養的發展，同時也涉及歸納推理、逆向思維等能力培養[6]．

2.3 浸潤德育美育的重要素材

在韋達定理發展的歷史長河中，一批批執著追求真理的數學家們前赴后繼，他們的故事、生平與成就中蘊含的理想信念與精神品質匯聚成莊重、嚴肅、令人敬仰的數學精神．教學中將數學史與數學精神滲透在定理的發現中，使其相互映照，讓學生在定理的學習中感悟數學精神、豐富歷史文化底蘊，并將精神融入學習生活中，指導學生未來的發展，達到數學史的“德育之效”．

此外，數學美是構成數學文化的重要內容，其實質在于理性精神和結構美．從價值追求上，韋達定理引導人們追求盡善盡美的理性精神；從表現形式上，韋達定理既包含著和諧美，也包含著簡潔美．和諧美體現于對稱式x+y和xy具有簡單和諧的對稱內涵[7]．簡潔美在于復雜的一元二次方程兩根之和與兩根之積僅用兩個系數的比值就能簡潔地表示出來．

3 啟示

3.1 對教師觀念的啟示

教師是教學的組織者，教師對待韋達定理的教學態度決定了其教育價值的發揮程度．在新課標頒布之前，有些教師就認為：韋達定理是選學內容，考試不作要求，就可以跳過該內容的教學，或讓學生自主閱讀教材就行．若直接“遺棄”韋達定理，這既不符合數學教學的全面性與基礎性，影響學生后續高中階段的學習，也喪失了培育學生數學核心素養、數學思想方法，滲透德育美育的重要契機，這對學生與教師而言都是一大遺憾．隨著新課標的頒布，教師先要擺正意識，正確地對待韋達定理的教學，積極研究教材、研究教學、研究學生，真正做到理解數學、理解教學、理解學生，將韋達定理的教育價值落到實處．

3.2 對教材編寫的啟示

教材是學生獲得數學知識的首要選擇，也是教師教學的重要參考．不同的教材對于韋達定理的編寫也有所不同，表1從定理發現、定理證明與例題內容三個方面比較了四個版本教材中對于韋達定理內容的編排與設計．

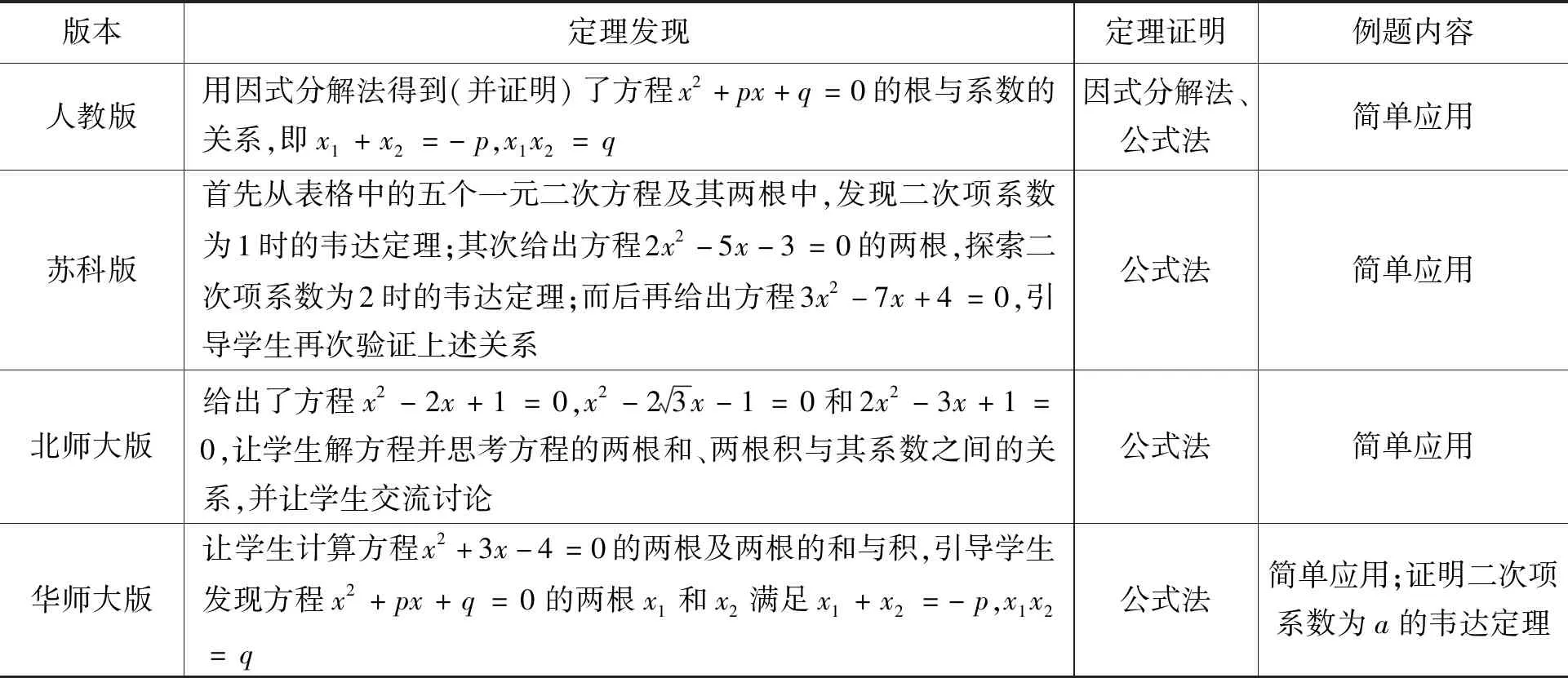
表1 四個版本教材中對于韋達定理內容的編排與設計

就定理發現而言，人教版從因式分解法出發，以邏輯推理(理性)視角發現定理，其他三個版本均從具體的方程出發，以數學猜想(感性)視角發現定理．就定理的證明而言，主要利用公式法證明，

其優點是貼合學生近期學習的內容，更方便、也更容易想到．但這種證明方法不符合歷史發展規律(先有韋達定理，后有求根公式)，并且一元五次及以上的高次方程沒有求根公式，該方法是無法推廣的；同時，用公式法證明也會讓學生產生對韋達定理學習意義的質疑，即：都能求出方程的具體兩根了，為何還要探究兩根之和與兩根之積．就例題內容而言，四版教材選取的例題都較為單一，只圍繞韋達定理的簡單應用(給出具體的一元二次方程，求出兩根和與兩根積)，沒有從定理逆用的角度選擇例題．

綜上，教材的編寫更側重于對定理本身的發現與探索，而忽略了韋達定理的發展歷史．為更好發揮韋達定理的教育價值，教材的編寫可以重構韋達定理的發展史，多角度融入韋達定理的不同證明方法，創設求根公式與韋達定理相互驗證的環節，并嘗試多方面地設置例題、分層次地設計課后練習，讓學生從教材中感受到韋達定理的歷史底蘊與價值．

3.3 對教學設計的啟示

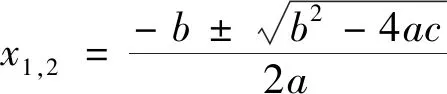
表2 韋達定理教學的五個環節的教學設計

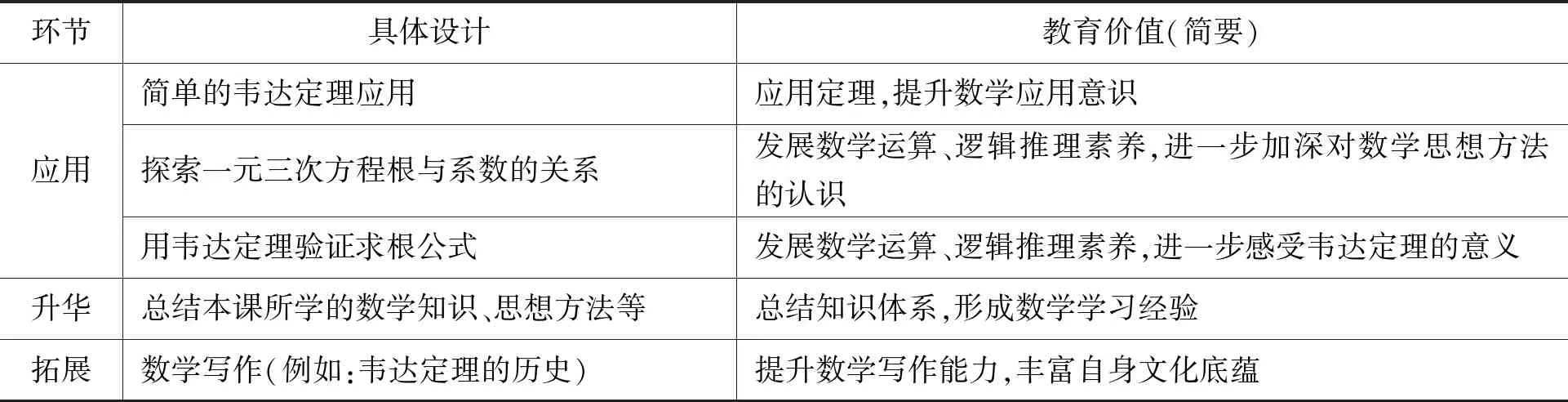
續表

3.4 對作業設計的啟示

在“雙減”的背景下，作業的設計更要體現診斷、鞏固、分析學情等功能，并鼓勵以分層、彈性和個性化的形式設計作業．新課標對于韋達定理的教學要求是“了解一元二次方程的根與系數的關系”[9]，因此，在韋達定理的作業設計環節更應立足基礎、指向文化，使不同層次的學生都得到相應的發展．為協調不同學生的知識基礎、思維模式以及學習能力存在的差異，教師可以設置分層、個性化、拓展性作業．例如，A層作業可以選擇課本中的習題，進行韋達定理的簡單應用，加深對韋達定理的認識；B層作業可以選擇韋達定理深入應用或涉及課堂數學思想方法的習題，如求證一元三次方程的韋達定理等等；拓展性作業可以數學寫作為載體，涉及韋達定理的歷史、探索韋達定理的“美”、韋達定理的證明、韋達定理與求根公式的關系、設而不求的思想及應用等主題，引導學生利用網絡資料、圖書館等收集相關材料，形成自己的“一家之言”，同時也激發學生的主觀能動性，為學生課外閱讀提供指導方向，并促使學生在閱讀整理中，提升數學素養、文化素養．

作業的設計與布置延伸了韋達定理的教學，讓學生在分層、個性化、拓展性作業中形成對韋達定理的多元化認識，使其教育價值真正在學生發展核心素養的道路上留下深深的“烙印”，成為他們未來數學學習旅途中的“寶藏”．