兩道“新距離”問題引發的思考*
陳元中 (安徽省合肥市第一中學高三35班 230601)
指導教師 洪雨沛 (安徽省合肥市第一中學 230601)
1 對兩道新定義類題目的思考
在高中數學中,新定義類題目因設問情境新穎,能夠凸顯學生的能力與素養,經常受到出題人的青睞.除了我們最熟悉的歐氏距離外,其他“新”的距離常被設置成具體情境考查學生.下面兩道題目分別定義了兩種全新的距離.
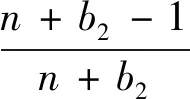
3 解題反思
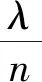
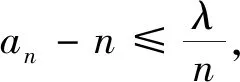
4 解法溯源
4.1 等差模型
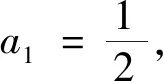
4.2 等比模型
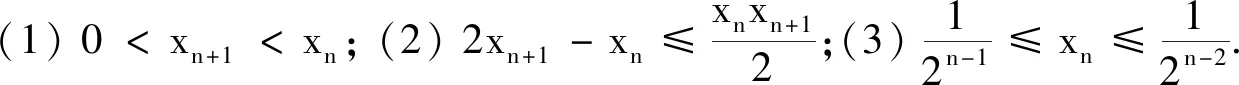
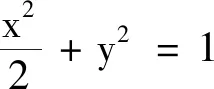
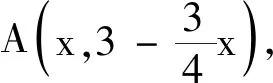
問題2在平面直角坐標系中,定義d(A,B)=max{|x1-x2|,|y1-y2|}為兩點A(x1,y1),B(x2,y2)的“切比雪夫距離”.又設點P及l上任意一點Q,稱d(P,Q)的最小值為點P到直線l的“切比雪夫距離”,記作d(P,l).
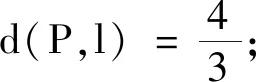
思路 其中①③的討論見后文.
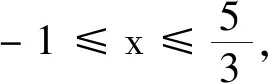
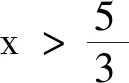
綜上,①②③正確.
2 兩種“新距離”
上述兩個題目定義了兩種不同的距離.經過查閱資料得知,我們最常使用的距離稱為歐幾里得距離,而問題1、問題2定義的這兩種距離分別被稱為曼哈頓距離和切比雪夫距離.距離究竟是怎樣的數學概念,這三種距離有怎樣的聯系與區別,筆者在R2空間中對三種距離進行了深入的探討.
2.1 距離的定義
我們所熟知的距離本質上是泛函分析中的一個基本概念.通過查詢相關材料,我們能夠得到距離的一般定義:
設X是任一非空集,對X中任意兩點x,y,有唯一確定的實數d(x,y)與之對應且滿足: ①非負性d(x,y)≥0,當且僅當x=y時d(x,y)=0;②對稱性d(x,y)=d(y,x);③三角不等式d(x,y)≤d(x,z)+d(z,y).稱d(x,y)為x,y之間的距離,(X,d)為度量空間.
我們不難發現歐氏距離顯然滿足上述定義.那么曼哈頓距離和切比雪夫距離是否滿足距離的定義呢?
2.2 曼哈頓距離
在R2空間中,A(x1,y1),B(x2,y2),則A,B兩點的曼哈頓距離可表示為d(A,B)=|x1-x2|+|y1-y2|.
由曼哈頓距離的定義易證非負性與對稱性,下面證明在曼哈頓距離下三角不等式是成立的:
設M(x3,y3),則d(A,B)=|x1-x2|+ |y1-y2|,d(A,M)=|x1-x3|+|y1-y3|,d(M,B)=|x3-x2|+|y3-y2|,則d(A,M)+d(M,B)=|x1-x3|+|y1-y3|+|x3-x2|+
|y3-y2|≥|x1-x3+x3-x2|+|y1-y3+y3-y2|=|x1-x2|+|y1-y2|=d(A,B).由此可知曼哈頓距離滿足距離的定義.
曼哈頓距離在實際生活中的應用十分廣泛.一個具有正南正北、正東正西方向規則布局的城鎮街道,從一點到達另一點的距離可以用南北方向與東西方向的距離之和表示,而這種形式的距離也就是曼哈頓距離,因此曼哈頓距離又稱為“出租車距離”(圖1).
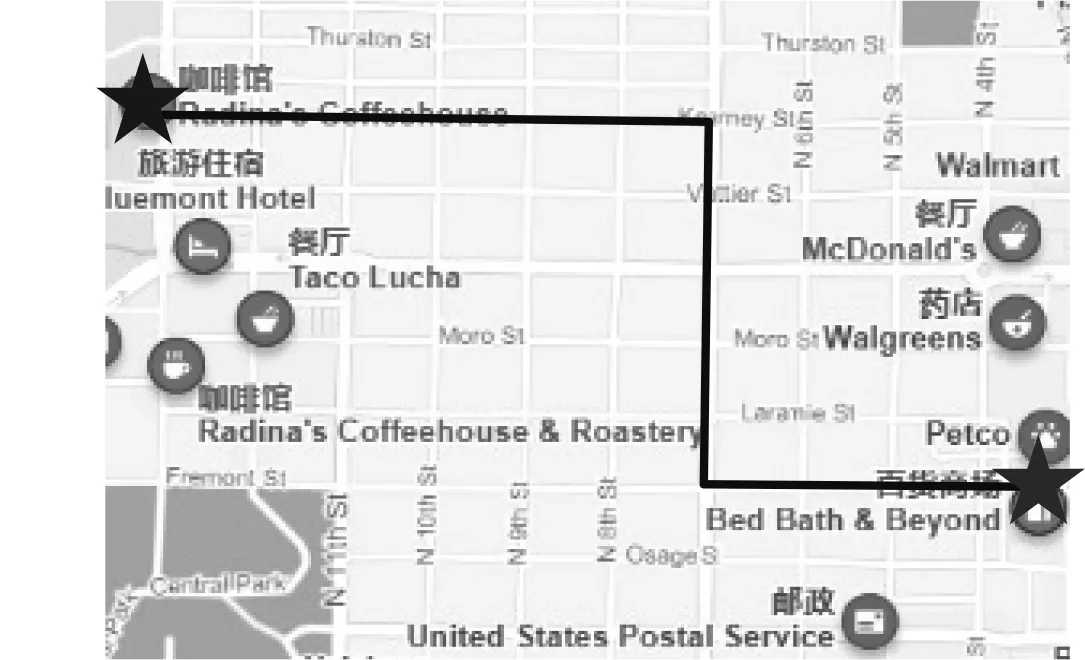
圖1 曼哈頓距離在城市 中的應用
在計算機圖形學中,屏幕由像素構成,顯示的每一個點都在像素上,用坐標的形式描述屏幕上的點,點的坐標也一般是整數.如果直接使用歐氏距離,則必須要進行浮點運算,而浮點運算很慢而且有誤差.如果使用曼哈頓距離,則只要進行加減法計算即可,這就大大提高了運算速度和運算精度.
但曼哈頓距離采用了將兩點之間的橫縱坐標絕對值的差之和作為刻畫距離的標準,多個距離間不方便運算,在這一方面,歐氏距離更占優勢.
讓我們再一次回看問題1,不難發現問題1所提出的距離就是曼哈頓距離,但是它刻畫的是點到直線的曼哈頓距離.
類比歐幾里得距離,猜測可以將點到直線上點的曼哈頓距離的最小值稱為點到直線的曼哈頓距離.
為了便于計算點到直線的曼哈頓距離,我們可以分兩種情況進行討論:(1)對于與x軸夾角小于45°的直線,曼哈頓距離即為過點的豎直直線與原直線相交形成的線段的長度;(2)對于與x軸夾角大于45°的直線,曼哈頓距離即為過點的水平直線與原直線相交形成的線段長度.下面對情況(2)作簡要證明.
如圖2,已知平面上有點A與直線l,AB平行于x軸,AB與l的夾角α>45°.M為l上除B外任一點,求證:d(A,M)>d(A,B).
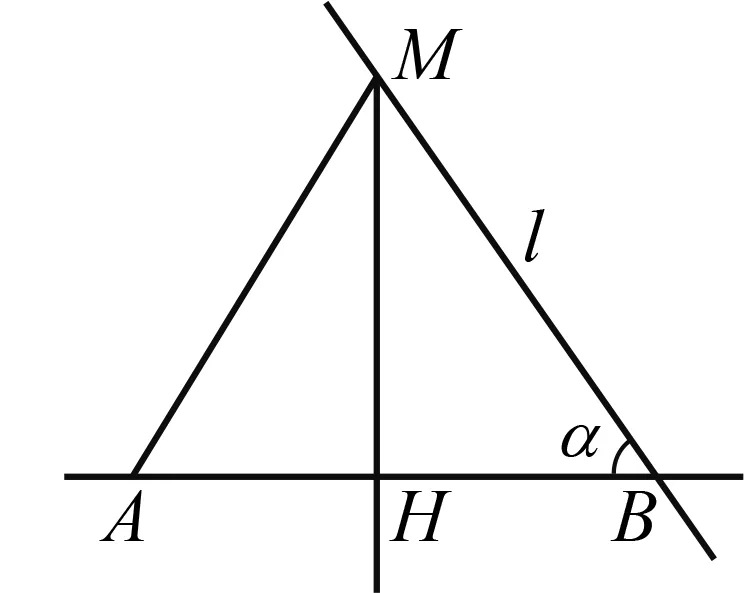
圖2
證明d(A,M)=AH+HM,d(A,B)=AB=AH+HB.因為α>45°,所以HM>HB,所以d(A,M)>d(A,B).
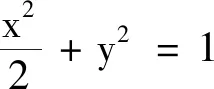
2.3 切比雪夫距離
在R2空間中,A(x1,y1),B(x2,y2),則A,B兩點的切比雪夫距離可表示為d(A,B)=max{|x1-x2|,|y1-y2|}.由切比雪夫距離的定義易證非負性與對稱性,下面證明在切比雪夫距離下三角不等式是成立的.
設M(x3,y3),則d(A,B)=max{|x1-x2|,
|y1-y2|},d(A,M)=max{|x1-x3|,|y1-y3|},d(M,B)=max{|x3-x2|,|y3-y2|},則d(A,M)+d(M,B)≥max{|x1-x3|+ |x3-x2|,|y1-y3|+|y3-y2|}≥max{|x1-x2|,|y1-y2|}=d(A,B).當且僅當A,B,M共線且M在線段AB上時等號成立.
由上可知,切比雪夫距離滿足距離的定義.
對于問題2中的③,本文給出分類討論的方法.對一般的點到直線的切比雪夫距離進行研究,過程較繁瑣,有興趣的讀者可以參閱文[1].
3 對三種距離的綜合理解
3.1 不同距離下的曲線形態
平面直角坐標系中,O為原點.接下來我們通過考慮方程d(O,A)=1所表示的曲線,來研究三種距離的聯系與區別.

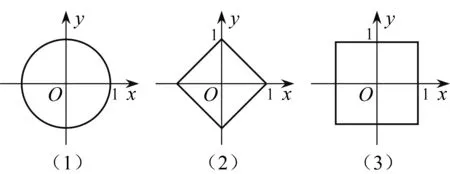
圖3 不同距離下的曲線形態
3.2 平面直角坐標系中切比雪夫距離與曼哈頓距離的轉化
同為正方形,曼哈頓距離與切比雪夫距離之間是否存在一定的轉化關系呢?
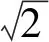

圖4 曼哈頓距離與 切比雪夫距離的變換
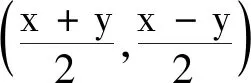
既然這三個距離之間有許多的性質極其相似,那么是否存在一個通式可以把三種距離統一起來呢?
3.3 閔可夫斯基距離
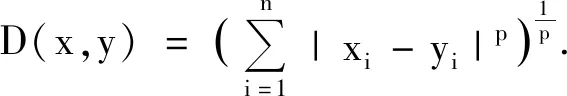
觀察這個式子,我們可以發現:當p=1時得到曼哈頓距離;當p=2時得到歐幾里得距離;當p→+∞時得到切比雪夫距離.以下對p→+∞時得到切比雪夫距離進行說明.

我們生活中隨處可見的距離,追根溯源,竟是十分高深的數學原理!上文所討論的三種距離竟然可以被統一為一個式子.這反映了在眾多繁雜的數學概念背后,其實隱藏著的都是相同的本質,就像一棵大樹,在外有眾多伸向四面八方的枝椏,但最終聯系它們的都是同一棵主干,這也體現了數學中萬變不離其宗的大道至簡之美.

