基于常時微動的建筑群振動特性及其抗震能力分布推測

于欣冉，那仁滿都拉，2，烏日圖那松，李鳳祥

（1.內蒙古師范大學 地理科學學院，內蒙古 呼和浩特 010022；2.內蒙古自治區蒙古高原災害與生態安全重點實驗室，內蒙古 呼和浩特 010022；3.錫林郭勒盟蒙古族中學，內蒙古 錫林郭勒 026000；4.內蒙古城市規劃市政設計研究院有限公司，內蒙古 呼和浩特 010070）

汶川地震災害的調查分析結果顯示，地震時建筑物抗震能力弱所導致的建筑結構受損是人員傷亡和直接經濟損失的主要原因之一［1-3］。我國部分老舊建筑物和經濟發展水平較低的中西部地區，建筑物的抗震性能并未滿足國家現行有關規范標準要求［4-6］，且該問題面臨的對象不僅是單個建筑物，而是建筑群。建筑群震害評估一般采用損害矩陣等經驗性函數［7-10］，但該方法難以體現建筑群實際抗震能力及易損性建筑物所需的加固程度。近年來，利用地震波和建立建筑物數值模型來演算建筑物抗震安全性能的研究明顯增多［11-14］，其中熊琛等［11-12］在建筑設計與實際信息基礎上建立了建筑群模型。該方法能很好反映建筑群受損機理的真實性和準確度，但以某個城市為對象時，很難對幾千棟甚至幾萬棟建筑群進行模型構建。因此，若能掌握既有建筑群的抗震能力分布規律，結合標準性建筑物模型，則更容易構建高精度建筑群模型。在建筑群抗震能力分布推測方面，柴田明德等［15-16］采用地震災情數據，提出了建筑物極限抗震能力分布規律，Nagato 等［17-18］利用該抗震能力分布規律構建了建筑群模型，并在建筑群震害評估中廣泛應用。在缺少地震數據的地區，針對建筑群開展常時微動觀測，分析其固有頻率的差異，成為判別建筑物實際抗震能力的最有效手段之一。寶音圖等［19］利用建筑物的常時微動觀測數據，分析固有頻率的平均值及標準偏差，構建了不同城市建筑群震害預測模型。那仁滿都拉等［20-21］采用常時微動觀測數據，建立了單個建筑物的剛度與抗震能力評估方法，提出了判斷建筑物抗震能力安全達標程度的簡易推測手段和建筑物的區域差異性［22-24］。傅光耀［25］采用常時微動觀測識別了高層建筑物的動力特征。吳志堅等［26］通過汶川震害調查證實了常時微動測試結果能較好地反映實際建筑物破壞情況。

為提高震害預測準確度，在城市既有建筑群震害評估中需要構建建筑群模型。但是，由于城市建筑群數量龐大、各個建筑結構選型不同和設計材料欠缺等問題，很難對所有建筑物構建數值模型。為掌握建筑群振動特性及其抗震能力分布，以呼和浩特市區鋼筋混凝土建筑群為例，首先在建筑群里選出不同樓層、不同年代、不同形狀的建筑物進行常時微動觀測，并實地調查收集建筑物的尺寸和用途等基本信息；其次，分析觀測建筑物的固有頻率來掌握建筑群的振動特征；最后，采用統計學方法，通過分析建筑物固有頻率的平均值及其分散特征，間接推測建筑群的抗震能力分布規律，以期為今后建筑群模型構建和城市震害評估提供參考依據。

1 研究方法

1.1 建筑物與觀測概要

為掌握建筑群整體振動特征，在呼和浩特市區范圍內，均勻選出不同樓層、建設年代、形狀和用途的431 棟建筑物進行常時微振動觀測，同時收集基層建筑面積、高度等基礎信息及相關建筑設計材料，其中約95%的建筑物在3～28 層間，建設年代在1979—2015 年間。觀測時間選在風小、無雨的白天。

觀測儀器為日本應用地質有限公司生產的常時微動儀（McSEIS-MT NEO），可測量水平2 個方向和垂直1 個方向的加速度成分，頻率范圍為0.1～200 Hz，放大器放大范圍為1～32 倍，并配有電子數據記錄器和GPS 天線。觀測方法是將2 臺儀器各置在建筑物的1 層（1F）和頂層或樓頂（R），1 層和頂層的儀器要盡量位于同一條鉛直線上且靠近建筑主體結構，儀器的朝向要與建筑物的長軸和短軸方向一致。此外，要用GPS 對準時間以確保2 臺儀器數據同步，每個建筑物觀測30～60 min。圖1 顯示儀器、建筑物觀測點（儀器位置）及儀器設置示例。

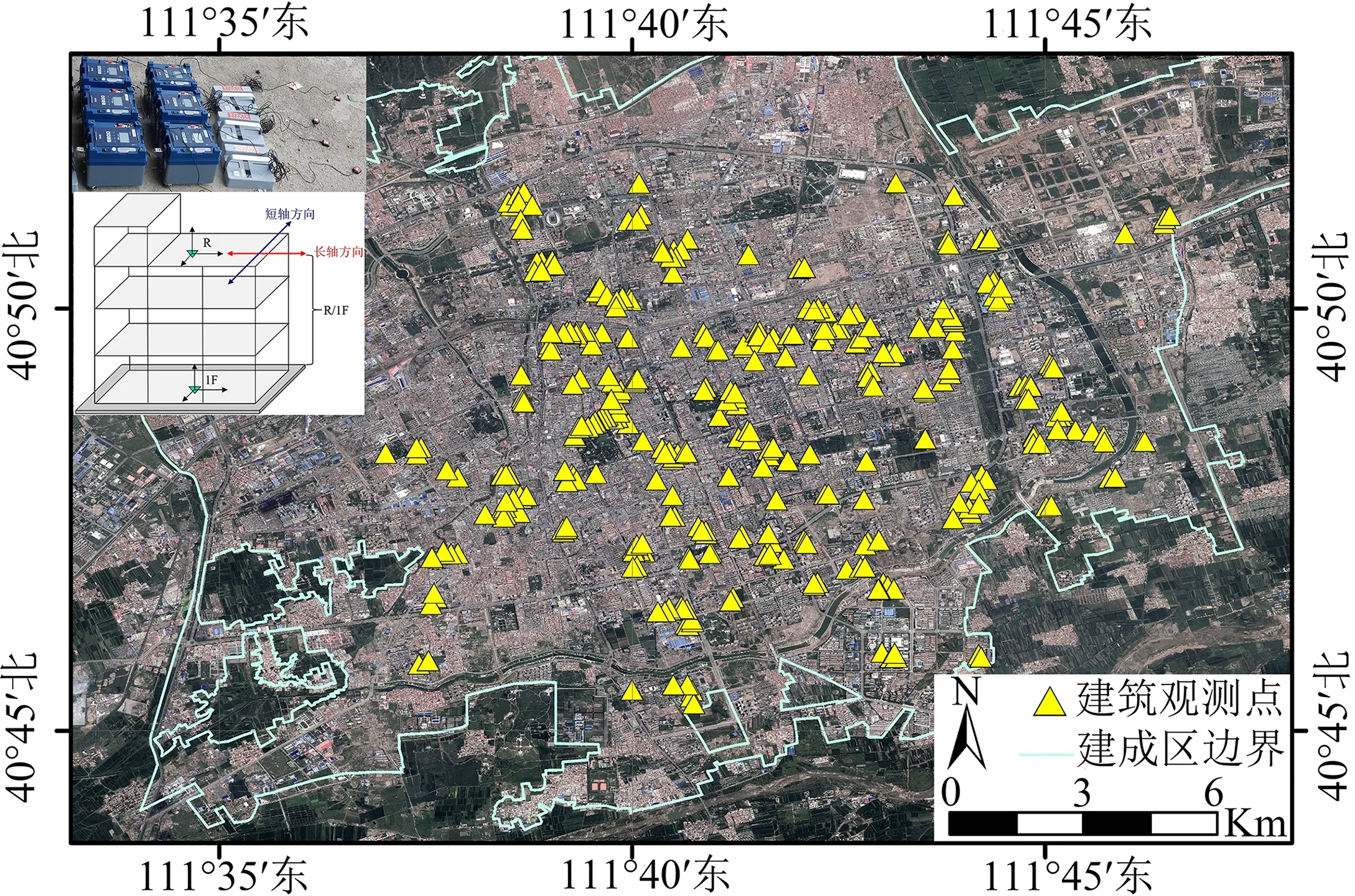
圖1 建筑物觀測點與儀器及其設置示例Fig.1 Buildings observation points and microtremor with setup

1.2 觀測數據處理

利用50% 重復的方式把觀測數據分割為若干個長為81.92 s 的時間窗，從中選出干擾少的時間窗對其進行快速傅立葉變換，獲得垂直成分與2 個水平成分的傅立葉頻譜及平滑化數據。再從頂層（或樓頂）和1 層傅立葉頻譜比的最大值處中讀取該建筑物的長軸與短軸方向的固有頻率［21］。

2 建筑群振動特征分析

2.1 不同樓層的建筑群振動特性

不同樓層建筑群固有頻率變化如圖2 所示，建筑群的固有頻率具有隨著層數的增多而減小的趨勢。該趨勢表明雖然建筑物的固有頻率是由質量和剛度決定的，但隨著建筑物層數的增多，質量或剛度也隨之變化，因此建筑群固有頻率與層數呈現出密切的相關特征。該特征的回歸方程在長軸和短軸方向上略微不同：fs=4.073e-0.068n，fl=4.059e-0.062n，其中fs，fl分別代表短軸和長軸的固有頻率，n為建筑物的樓層數。

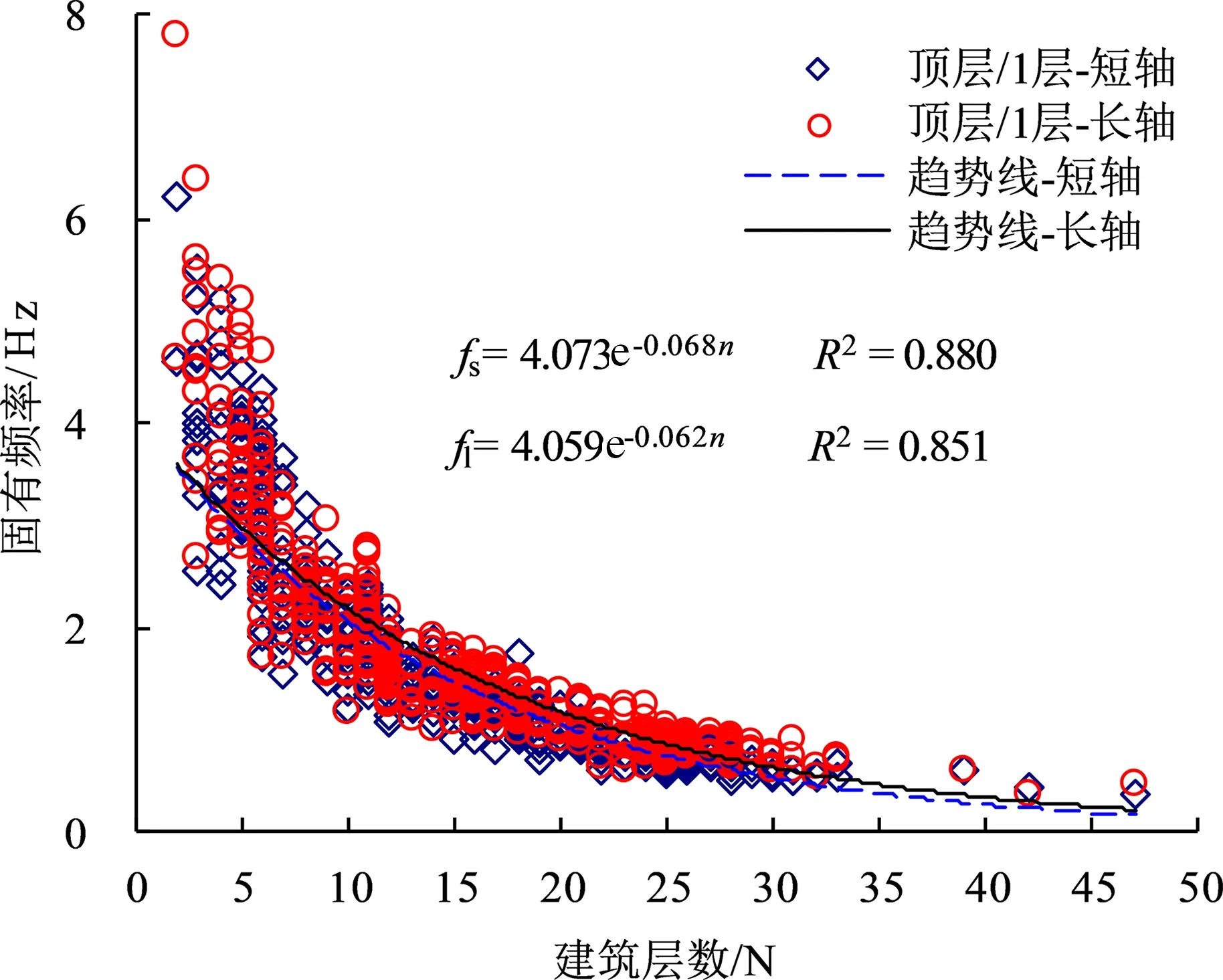
圖2 不同樓層建筑群固有頻率Fig.2 Intrinsic frequencies of buildings on different floors

2.2 不同方向的建筑群振動特性

筑物的長軸方向上布置了更多的承重墻、梁和柱子等，導致長軸的抗側剛度大于短軸的抗側剛度。長軸方向上布置了更多的承重墻、梁和柱子等，導致長軸的抗側剛度大于短軸的抗側剛度。置了更多的承重墻、梁和柱子等，導致長軸的抗側剛度大于短軸的抗側剛度。

2.3 不同用途的建筑群振動特性

依據建筑物用途可以將其劃分為住宅建筑和非住宅建筑。住宅建筑主要供居住使用，非住宅建筑主要包括辦公、商業、教學和寫字樓等。這兩類建筑群的固有頻率與樓層數的關系如圖4 所示。從圖4 可知，不論是長軸方向還是短軸方向，大多數住宅建筑物的固有頻率值要大于非住宅建筑物。這可能與建筑結構類型和建筑自身形狀及其空間格局有關。調查發現，研究區為剪力墻結構的住宅建筑物的比例要比非住宅建筑物的多約21%，同時與非住宅建筑物相比，住宅建筑物的開間較小、柱距較小、墻體較多。

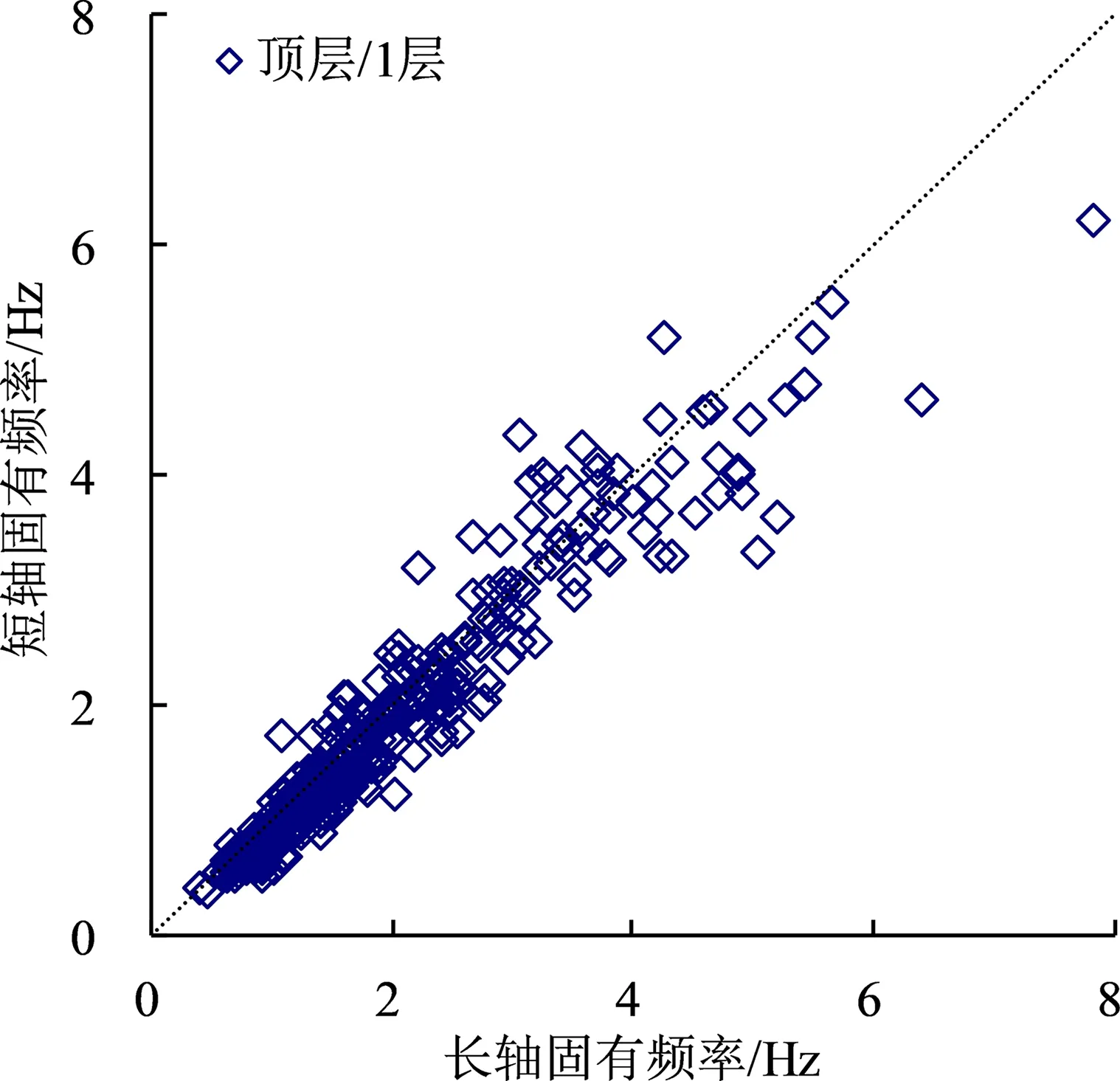
圖3 建筑群長軸方向和短軸方向固有頻率比較Fig.3 Comparison buildings intrinsic frequencies in long and short axis directions

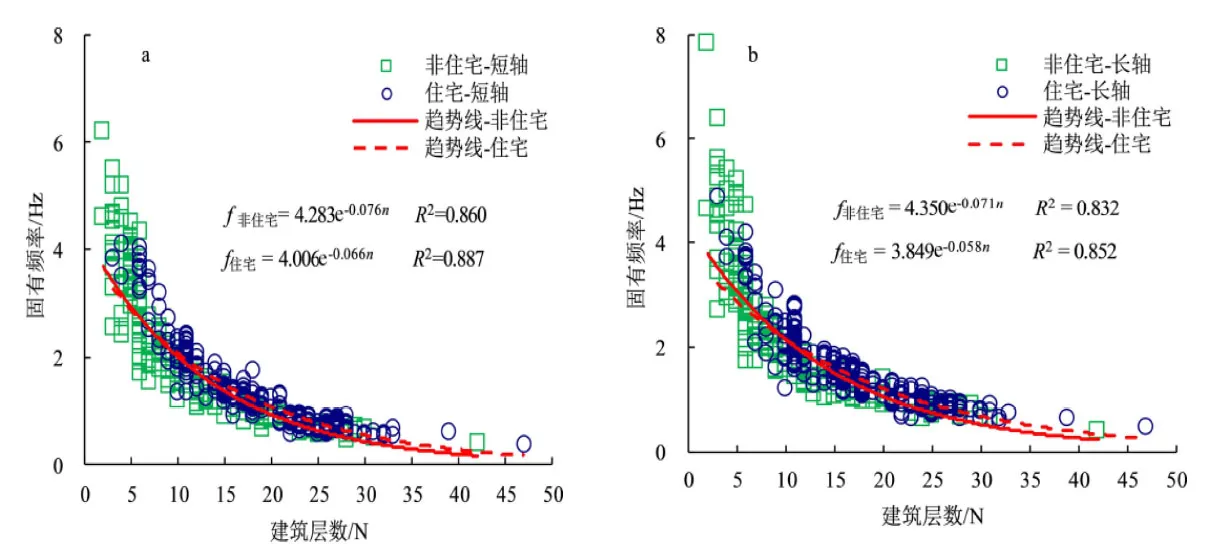
圖4 住宅用途和非住宅用途建筑群固有頻率比較Fig.4 Comparison of the intrinsic frequencies of residential and non-residential use building groups

3 建筑群抗震能力分布規律的推測方法

3.1 建筑群抗震能力分布規律推測的理論依據

固有頻率（f）是建筑結構的主要動力特征指標之一，由建筑物的質量（M）和剛度（K）所決定［27］，三者關系為：K=4π2Mf2。質量同等時，建筑物的剛度與其固有頻率的平方成正比例關系。因此可通過規模與層數相同（4π2M一定值）的建筑群觀測固有頻率與平均固有頻率的比值，即標準化固有頻率的二次方的分布特征，推測該同層數建筑群的剛度分布規律，推測過程如圖5 所示。實際工作中不易獲取建筑物的極限抗震能力，一般先獲取建筑物的剛度，再根據建筑物的剛度和抗震能力間的正比例關系來構建建筑群模型［19，21］，因此獲得的建筑群剛度分布規律可間接反映其抗震能力分布規律。

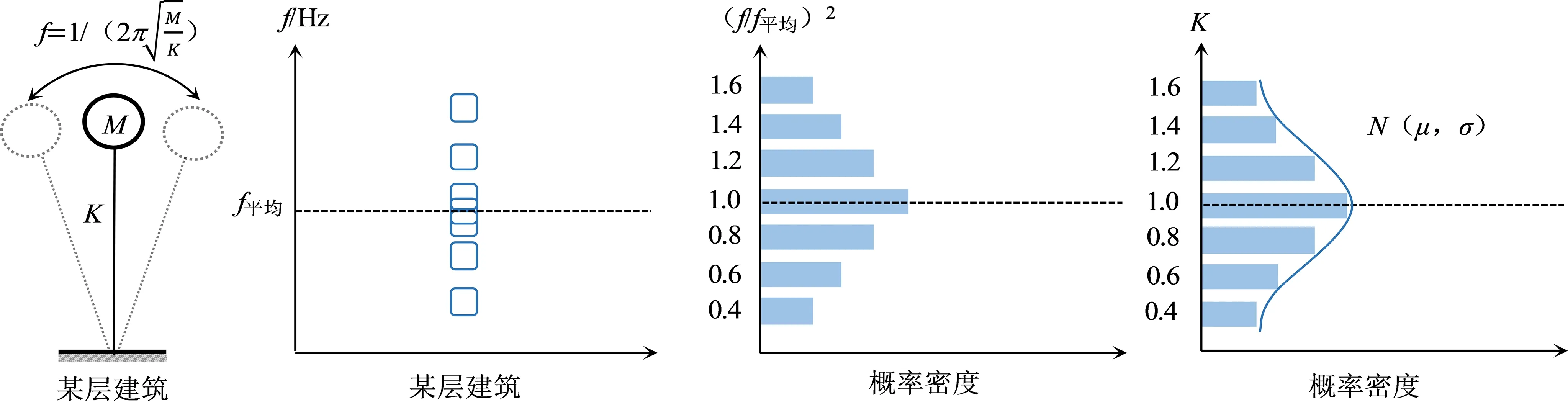
圖5 建筑物抗震能力分布推測過程Fig.5 Process of estimating the seismic capacity distribution of buildings

3.2 推定建筑群抗震能力分布規律

根據上述理論和柴田建筑群抗震能力分布推測方法［15-16］，首先根據圖2 所得的建筑物固有頻率與層數間的回歸公式，計算出不同樓層建筑物短軸和長軸方向的平均固有頻率，定為標準固有頻率。其次用該層的觀測固有頻率除以標準固有頻率，計算出標準化固有頻率，再以標準化固有頻率的2 次方作為一個連續型隨機變量，求其頻度分布并除以觀測的建筑群總數，計算出概率密度。最后運用對數正態概率密度函數N(σ，μ)來擬合它的分布，得到短軸方向和長軸方向的對數正態分布曲線，即觀測建筑群的剛度分布規律，如圖6 所示。可知1 附近的概率密度最高，主要分布在0.45～2.9 之間，并且建筑物的短軸方向和長軸方向的剛度分布特征較接近，說明雖然建筑物不同方向的振動特性不同，但其剛度分布規律與建筑物的方向幾乎無關。

圖6 觀測建筑群的概率密度與擬合曲線Fig.6 Probability density of buildings with fitted curves

呼和浩特市區建筑群的整體剛度分布曲線和柴田明德推測的日本東北地區（6 縣245 棟1～5 層鋼筋混凝土結構）建筑群的極限抗震能力分布曲線［15-16］的比較如圖7 所示。表1 給出了與兩條曲線相應的參數（σ，μ）。該曲線代表不同剛度的建筑物占比，峰值處為標準剛度的建筑比率，峰值左側曲線代表剛度低于標準剛度的建筑物比率，峰值右側曲線代表剛度高于標準剛度的建筑物比率。可以看出，建筑群的整體剛度特征分布曲線與柴田曲線類似，但柴田曲線右側方向分散得更明顯。圖8 進一步比較了標準、超標準（峰值右側）和不滿足標準（峰值左側）建筑物的存在比率。由圖8 可知，研究區抗震能力偏低的建筑物存在比率（41%）和抗震能力偏高的建筑物存在比率（40%）幾乎相同。而日本東北地區抗震能力偏低的建筑物存在比率（32%）遠小于抗震能力偏高的存在比率（50%）。由此可得呼和浩特市區的抗震能力低于標準抗震能力的建筑物要比日本東北地區多9%。

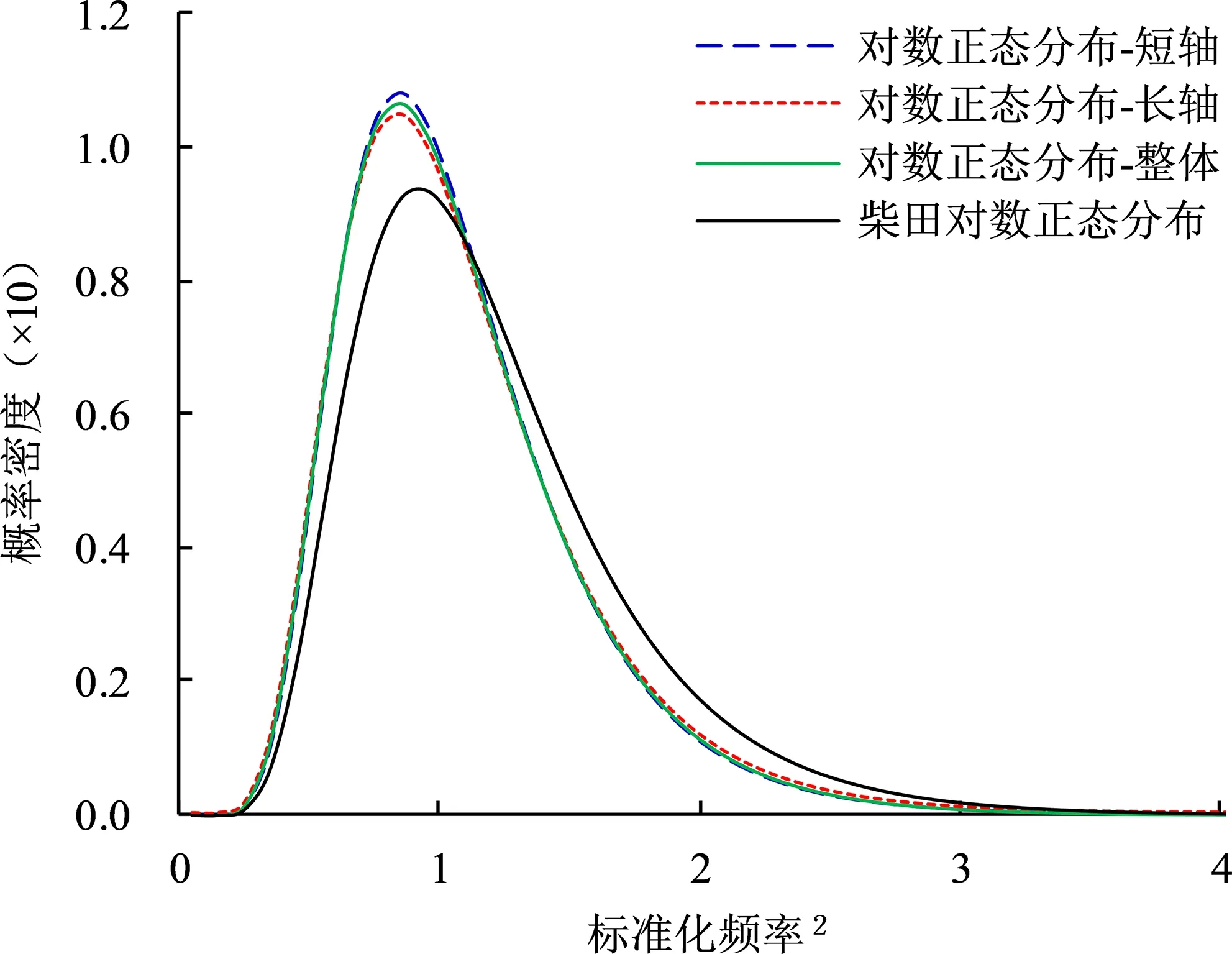
圖7 觀測建筑群對數正態分布曲線Fig.7 The logarithmic distribution curve of buildings

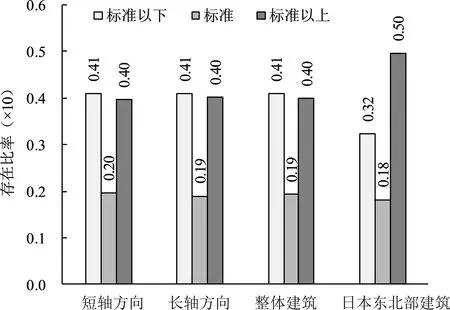
圖8 存在比率的比較Fig.8 Comparison of existing ratios

由于建筑物的用途不同，抗震能力也可能不同，因此以同樣的方法推測了住宅和非住宅建筑群的剛度分布規律曲線及其公式系數，如圖9 和表1 所示。可以看出不同用途的建筑群剛度分布規律曲線存在明顯差異。住宅建筑的剛度分布比較集中于峰值附近，而非住宅建筑的比較分散，并且剛度低于標準建筑物的非住宅建筑物比率要比住宅建筑物多。因此，在住宅和非住宅建筑物的標準抗震能力同等條件下，非住宅建筑物在地震當中更容易出現受損現象。以上結果與一般住宅建筑物的柱、梁、承重墻等主體結構較多，而非住宅建筑物其內部空間相對較大，主體結構較少和住宅建筑物與非住宅建筑物相比更單一等的實際情況較為符合。說明推測的對象建筑群抗震能力分布曲線具有一定可靠性與實用性。

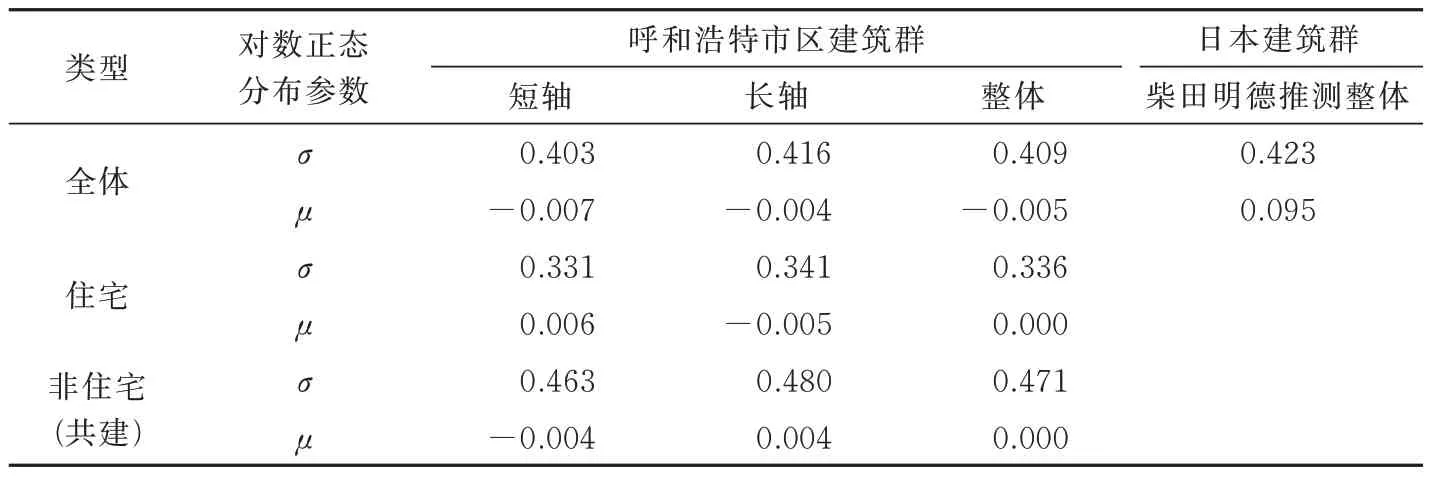
表1 觀測建筑群剛度分布公式系數Tab.1 Observed building stiffness distribution formula coefficients

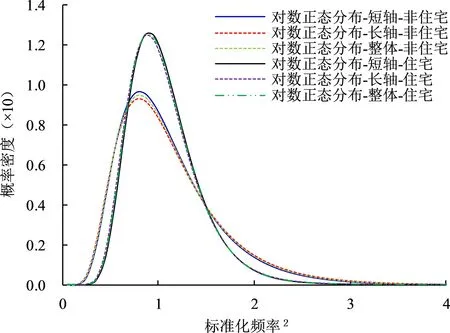
圖9 住宅與非住宅建筑物對數正態分布曲線比較Fig.9 Comparison of log-normal distribution curves for residential and non-residential buildings

4 結論

為掌握既有建筑群的振動特征及其抗震能力分布規律，在呼和浩特市區內選出不同建筑年代、高度、樓層、形狀和用途的431 棟鋼筋混凝土建筑物進行常時微動觀測與實地調查，獲取了建筑群的固有頻率。采用統計學方法，通過分析固有頻率的平均值及其分散特征，推測建筑群的抗震能力分布規律。得出的結論如下：

（1）不同樓層建筑群的固有頻率不同，層數越多的建筑物固有頻率越小，回歸公式為fl=4.059e-0.062n，fs=4.073e-0.068n。

（2）建筑物的形狀直接影響建筑結構的振動特性，大部分建筑物的短軸方向的固有頻率與長軸方向相等或偏小。

（3）不同用途建筑群的固有頻率不同，分析結果表明大多數住宅用途建筑物的固有頻率要大于非住宅用途建筑物。

（4）建筑群在短軸方向和長軸方向的抗震能力分布規律基本一致。研究區全體建筑群抗震能力分布對數正態分布曲線的標準偏差為0.409，平均值為-0.005。用途不同建筑物的抗震能力分布特征也不同，住宅建筑物抗震能力分布比較集中于標準值附近，而非住宅建筑物的較為分散。

（5）通過對比呼和浩特市區建筑群抗震能力分布曲線與日本東北地區柴田抗震能力分布曲線，發現呼和浩特市區的抗震能力低于該地區標準建筑物的存在比率為41%，比日本東北地區多9%。今后需要加強震害評估和減災防災工作力度。

目前初步提出了基于常時微動觀測的建筑群抗震能力分布規律間接推測方法，下一步擬構建建筑群模型，評估呼和浩特市區建筑群震害損失及脆弱性建筑物所需加固程度，從而為震害風險大、防震技術薄弱的中西部經濟欠發達地區的可持續發展提供安全保障。