基于車橋耦合振動的連續梁橋動力響應分析

彭偉康高慶飛徐昭若王統于曉梅

(1.哈爾濱工業大學 交通科學與工程學院,哈爾濱 150001;2.大連理工大學 建設工程學部,遼寧 大連 116024;3.東北林業大學 圖書館,哈爾濱 150040)

0 引言

車橋耦合振動(Vehicle-bridge Coupling Vibration)即為當車輛在橋梁上前進時,車輛由于車身與橋梁表面的接觸和橋面的不平整度引起車身的振動,而橋梁又由于車輛的振動而引起橋體的振動,車輛與橋梁之間相互作用、相互影響,產生的車輛與橋梁之間的共同振動。

自19世紀初,英國第一條鐵路橋梁修成以后,工程師們便開始發現車橋耦合振動方面的問題,并開始進行研究[1]。其早期的研究方法有試驗研究法和古典解析法,自20世紀中期,隨著電子計算機的發明,有限元技術的提出,數值模擬法也得到應用。數值模擬法的應用和發展,使得鐵路橋梁的車橋耦合振動建立的模型更加貼近現實,振動響應的計算也更加接近實測。早期的車橋耦合振動研究幾乎都是應用于鐵路橋梁的,而隨著近現代經濟的發展和車輛的普遍使用,公路橋梁的車橋耦合振動問題也得到了越來越多的研究[2-4]。對于汽車-公路橋梁耦合振動的研究,最早可追溯到從19世紀末開始的試驗研究法,相繼有法國工程師、英國土木工程師協會和瑞士聯邦材料科學與技術實驗室進行了橋上動力荷載試驗,并收集了大量汽車行車實測數據進行分析[5];20世紀80年代以來,國內也有吳啟宏[6]、項貽強等[7]進行橋梁動力分析的試驗研究,并獲得動力系數、橋梁自振特性等結論。同時,為更好地認識車輛和橋梁之間的動力學關系,學者們的理論計算方法也投入使用,早期采用的計算方法有將車輛荷載簡化為常量力、簡諧力和滾動質量塊等的解析計算法,通過多種解析計算方法的計算結果進行對比可知,車輛質量較大時車輛慣性力對于橋梁振動的響應有較大的影響[8]。公路橋梁的數值模擬法大約在20世紀70年代開始研究,國外及國內的學者均從車輛模型、橋梁模型和動力學方程求解3個方面進行不斷的深入探索。對于車輛模型的建立,學者們最初使用的有四分之一車輛模型或二分之一車輛模型,近年來,為追求更高的模擬精度,國內外眾多學者均建立了三維多自由度的車輛模型,如王鐵龍等[9]、Obrien等[10]分別建立了三軸或五軸的卡車模型來進行車輛荷載的模擬;隨著有限元軟件的不斷進步,橋梁模型的建立也在朝著完善的方向發展,從早期的桿系模型,空間梁格模型[9],到相對更加準確的實體模型,雖然實體單元模型能給中小跨徑橋梁帶來更高的精度,但也明顯提高了較大跨徑橋梁的計算規模,帶來一定的計算壓力,故多尺度模型[11]也可為大跨徑橋梁帶來一個重要的發展方向;依據橋梁與車輛的有限元模型,建立車橋耦合振動系統的動力學方程后,學者們求解動力學方程的方法可分為直接積分法和模態綜合法,直接積分法可以將車輛動力學方程和橋梁動力學方程進行分組迭代求解[12],也可以將車輛動力學方程和橋梁動力學方程合并整體求解[13],模態綜合法則將動力學方程進行振型疊加,簡化自由度數目過大的動力學方程進行求解[9]。基于汽車-公路橋梁耦合振動的理論方法研究,動力放大系數可以較好地表征移動車輛對橋梁的沖擊效應,同時也是各國橋梁規范中一個重要參數-沖擊系數的計算方法。如今各國規范中所采用的沖擊系數計算方法仍然存在較大的差異[14],眾多學者的近期研究也認識到橋梁的沖擊系數與橋梁結構類型、車速和車重等多種因素有關,各國規范所描述的沖擊系數表示方法仍有一定偏差,需繼續進行優化[15]。

本文主要闡述車橋耦合振動的基本理論與分析研究方法,并利用ANSYS軟件對跨徑為30 m×5 m的五跨連續梁橋進行車輛過橋的數值模擬,分別計算出橋梁在汽車靜力荷載和動力荷載作用下的靜力響應和動力響應,分析動力響應與靜力響應比值(動力放大系數)的變化規律。對于橋梁的荷載響應而言,橋梁各個位置處的撓度、應力等均可作為其荷載響應,且每對動力響應與靜力響應的比值也均可作為其動力放大系數,故本文也將從撓度、應力2個方面去分析標準橋梁的動力放大系數。

1 車橋耦合振動分析方法

車輛駛入橋梁以后,運動過程十分復雜,影響車橋耦合振動的因素很多,如車輛橋頭跳車、行駛的變速(包括剎車)和路面的粗糙度等[16-18]。車橋耦合振動的分析方法有室內試驗和現場試驗的試驗研究法、解析計算和數值模擬的計算研究法。現場試驗研究實測所得的橋梁動力響應數據顯然是最真實可靠的,眾多學者[19-20]均進行了現場試驗研究,然而僅靠現場試驗研究來找到各種不同類型、不同尺寸橋梁在不同車輛行駛作用下的振動響應規律和其內運行機理,顯然是不經濟不現實的。相對于現場試驗而言,室內試驗可以較好控制車輛和橋梁的各項參數,能更好降低試驗成本,反映車橋實際規律。解析計算即利用簡單的簡支梁、固端梁或者連續梁模擬橋梁,簡單的常量力、簡諧力、滾動質量塊或者移動彈簧-質量塊來模擬行駛車輛,建立簡化模型進行理論推導,探尋車輛過橋動力響應基本規律。顯然解析計算所得的簡化計算結果與實際尚存在較大出入,但其為數值分析計算提供了理論基礎。數值模擬分析計算即通過計算機來建立不同的橋梁與車輛的有限元模型,并通過對模型和模型之間的相互作用的數學表達來建立相關的動力學耦合方程,最后使用合適的微分方程解法完成動力學方程的求解,計算獲得車橋動力響應特征。

1.1 數值模擬法

近些年對于車橋耦合問題,所采取的主要方法即為數值模擬法。進行數值模擬法,一般以剛體動力學方法建立車輛模型,以有限元方法建立橋梁模型,將車輛模型與橋梁模型分別作為2個子系統,再通過車輪與橋梁表面之間的位移協調、相互作用力大小相等的關系,使2個子系統的動力方程相聯系,采用迭代法求解系統響應結果。其中車輛動力學模型由車體、車輪、彈簧和阻尼器組成,車輪與車體、車輪與橋面均由彈簧和阻尼器連接,車輛模型的自由度主要由車輪個數和車體個數來決定[21]。橋梁通過有限元模型進行模擬,有限無模型常用的單元類型有桿系單元、板殼單元和實體單元等,單元的選擇應根據橋梁形狀特征、受力特點和精度要求等因素綜合考慮。各類不同的橋梁和不同的要求下,會有不同的橋梁建模類型,如:單梁或多梁的桿系模型、用等效梁格模擬上部結構的梁格模型、實體單元的精細化模型和局部小尺寸精細單元模擬的多尺度模型等[22-23]。

1.2 車橋耦合振動方程建立

進行數值模擬法的基本步驟為先建立車輛動力學模型,并建立車輛振動方程。車輛模型可擁有不同個數的車體,不同個數的輪軸,一般單個車體取浮沉、橫移、點頭和側滾4個自由度,每個車輪取升降和橫移2個自由度,通過拉格朗日方程即可推導出車輛運動方程

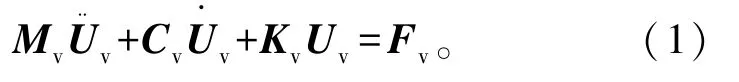
式中:Mv、Cv、Kv分別為車輛的質量矩陣、阻尼矩陣和剛度矩陣;分別為車輛各個單元的位移向量、速度向量和加速度向量;Fv為橋梁與車輛接觸點處對車輛的作用力向量。

繼而建立合適的橋梁模型,并建立橋梁振動方程

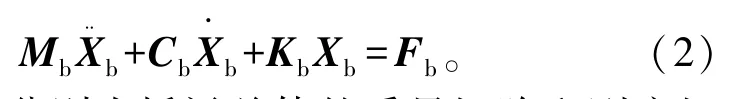
式中:Mb、Kb分別為橋梁總體的質量矩陣和剛度矩陣,一般采用有限元方法建立,Cb為總體阻尼矩陣,一般通過質量矩陣和剛度矩陣計算獲得;分別為橋梁各個單元的位移向量、速度向量和加速度向量;Fb為車輛作用在橋梁上的作用力向量。

然后將橋梁運動方程各模態坐標下動力響應疊加分析,化簡橋梁的質量矩陣、阻尼矩陣和剛度矩陣,簡化計算,得到模態綜合分析下的橋梁結構運動方程

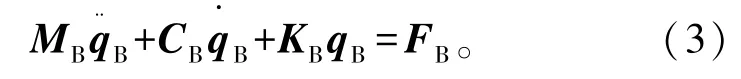
式中:MB、CB、KB分別為橋梁的質量矩陣、阻尼矩陣和剛度矩陣通過動力學方程的模態變換而得到的模態質量、模態阻尼、模態剛度矩陣;qB、FB則分別為橋梁有限元模型的廣義位移向量和廣義力向量。

聯立車輛和橋梁振動方程,并考慮位移協調條件和相互作用力相等條件,便可得到如下車橋耦合振動方程

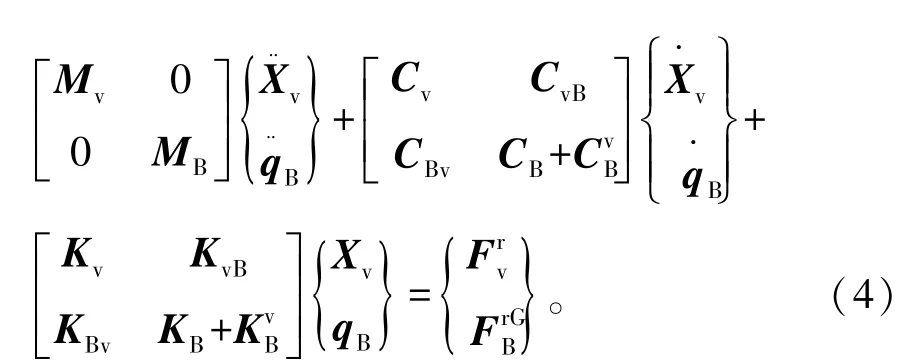
即為求解車橋耦合振動方程,其常使用的動力學方程求解方法為Newmark-β法。

2 有限元模型建立

本文選用《中國公路橋涵通用圖》中常用的,具有代表性的裝配式預應力混凝土連續T梁橋作為動力放大系數分析模型,橋梁為五跨連續梁橋,單跨跨徑為30 m,廣泛用于雙向四車道,橋梁的橫截面如圖1所示。

連續梁橋利用ANSYS軟件建立有限元模型,采用BEAM188單元建立橋梁的梁體,中間一處橋墩的位置設置縱向、豎向和橫向3個方向的約束,其余橋墩或橋臺位置處設置縱向和豎向2個方向的約束。同時為讓有限元模型更貼近實際,本文采用梁格模型對5片T形梁之間的橫向連接進行模擬,縱向設置5片T形梁截面之后,橫向設置剛度相等、質量為零的虛擬橫梁,縱梁與虛擬橫梁共同承受車輛荷載作用。建立所得的有限元模型如圖2所示。

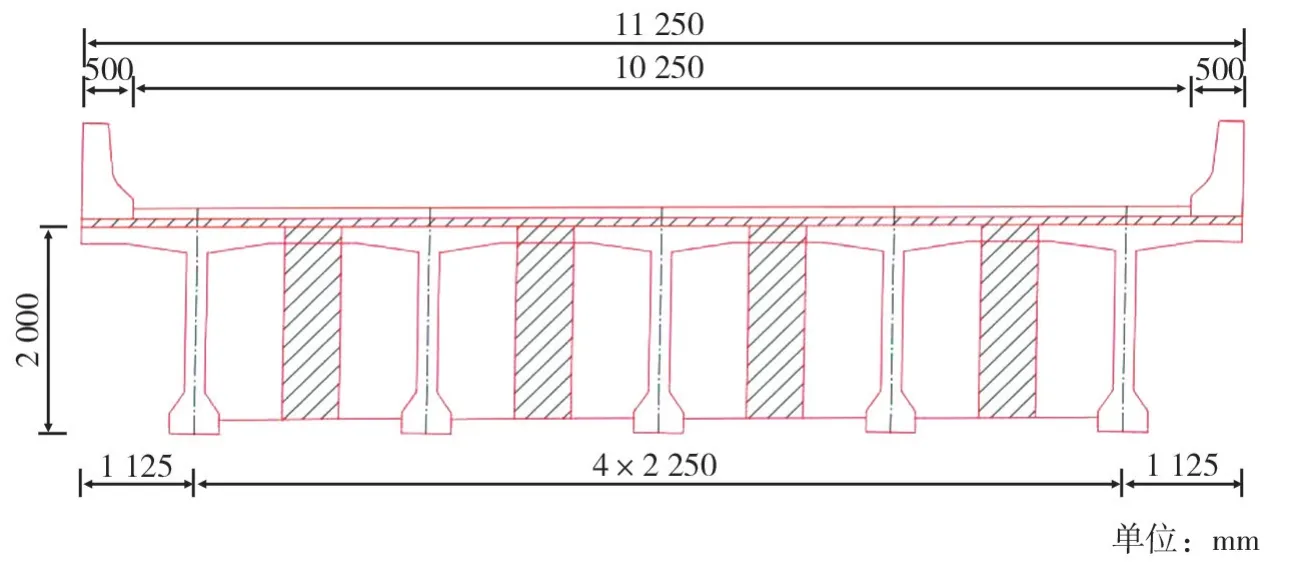
圖1 多跨連續梁橋橫截面Fig.1 Cross section of multi-span continuous girder bridge

圖2 ANSYS有限元模型Fig.2 ANSYS finite element model

基于ANSYS軟件建立的橋梁有限元模型,首先在模型中梁的各跨跨中施加車輛靜力荷載,設置車輛荷載為30 t,橋梁混凝土彈性模量為3.45×104MPa,分析計算得5片單梁的各跨跨中撓度,計算結果見表1。同時分別利用ANSYS軟件計算得到有限元模型在中梁各跨跨中施加靜力荷載時所產生的應力云圖,計算結果如圖3—圖5所示。

式中：i為年份，j為指標序號，aij為指標數據原始值，bij為標準化值，amax、amin分別為第j指標的最大值和最小值。

從橋梁的有限元模型在靜力荷載作用下所產生的3個應力云圖可以看出,在重力作用下邊跨處產生最大應力,中跨次之,次邊跨處最小;車輛荷載作用在邊跨時產生的橋梁最大應力為7.13×106N/m2,作用在次邊跨時產生的橋梁最大應力為6.55×106N/m2,作用在中跨時產生的橋梁最大應力為5.60×106N/m2,可見邊跨處荷載產生的應力最大。

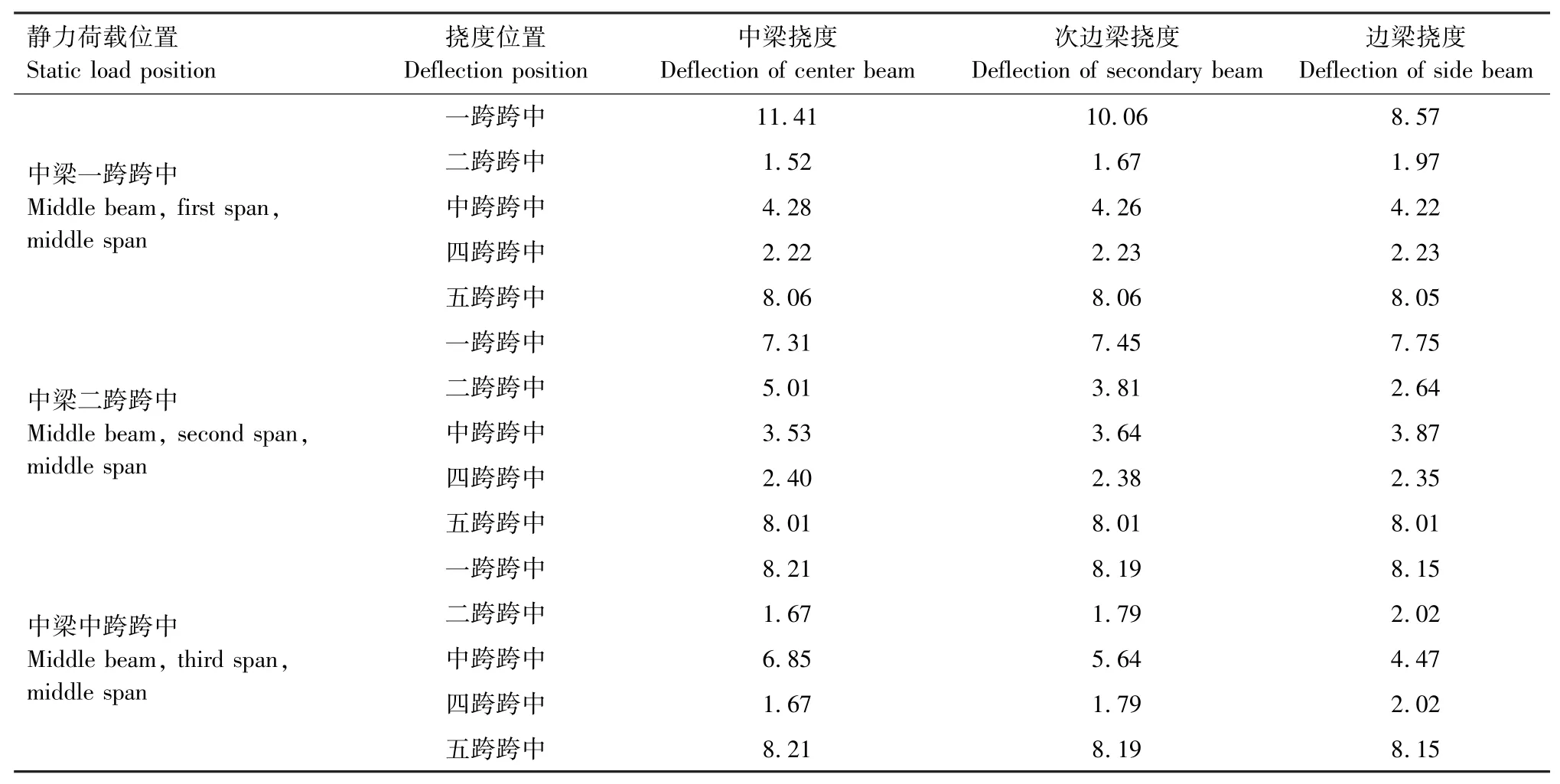
表1 中梁各跨跨中施加靜力荷載的撓度Tab.1 Deflection caused by static load applied in each span of the center beam mm

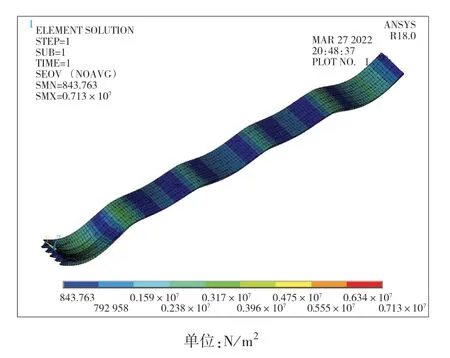
圖3 一跨跨中車輛荷載作用下應力云圖Fig.3 Stress nephogram under vehicle load in first span

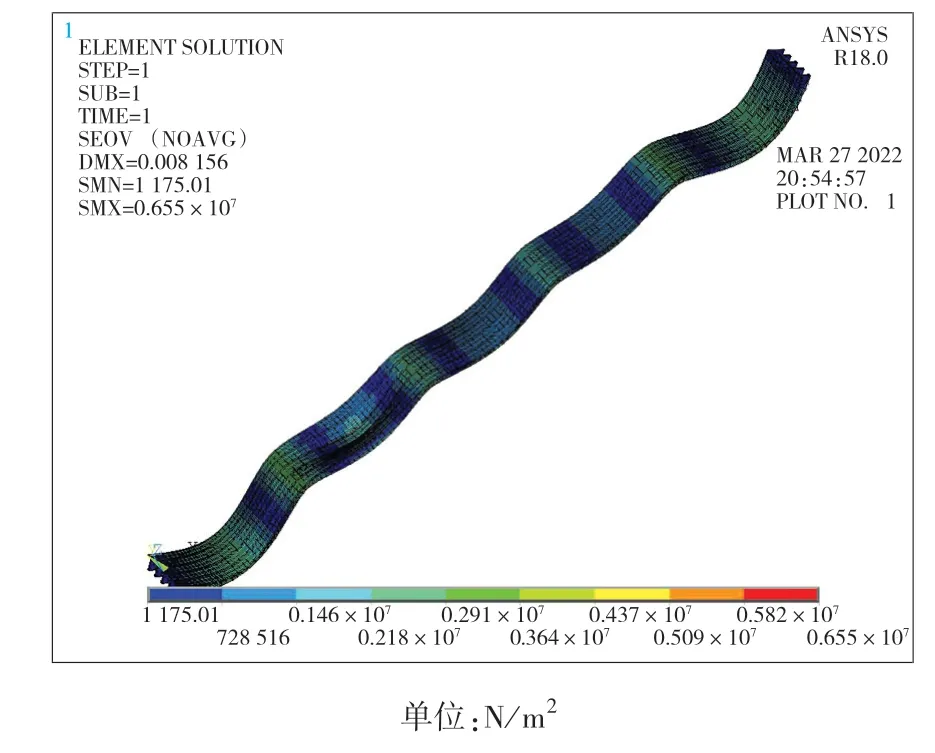
圖4 二跨跨中車輛荷載作用下應力云圖Fig.4 Stress nephogram under vehicle load in second span

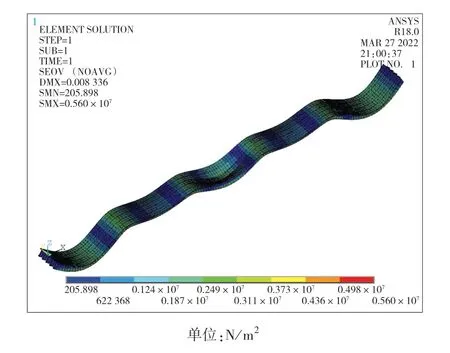
圖5 三跨跨中車輛荷載作用下應力云圖Fig.5 Stress nephogram under vehicle load in third span

通過靜力荷載作用下的橋梁撓度數據和應力云圖結果分析可知:橋梁在大型貨車的荷載和自重荷載的作用下,可以產生的最大靜撓度約為11 mm;在自重荷載的作用下,邊梁的跨中撓度最大,次邊梁的跨中撓度最小;在中梁的各跨跨中施加靜力荷載,可以得到施加荷載的橋梁跨中位置處中梁撓度最大,次邊梁略小,邊梁最小。由此可確定橋梁模型受力特性符合實際情況。

3 數值仿真結果

3.1 動力放大系數計算

動力放大系數即為橋梁在汽車動力荷載和汽車靜力荷載作用下最大動力響應與最大靜力響應的比值,本文選用五跨連續梁橋,分別選取其邊跨跨中、次邊跨跨中和中跨跨中3個位置的最大荷載響應進行研究,計算并比較其動力放大系數[24-25]。

動力放大系數計算即利用ANSYS軟件進行有限元分析可得到橋梁3個跨中位置在車輛經過橋梁時所產生的荷載效應,本文對3個跨中位置處的撓度、應力2個荷載效應分別進行研究,濾去產生荷載效應中的橋梁自重荷載,比較其車輛動力荷載效應和最大靜力荷載效應[26]的比值。圖6為五跨連續梁橋在車輛靜載作用下的中跨跨中撓度隨車輛位置變化的曲線(靜撓度),和車輛以20 m/s行駛過橋梁時中跨跨中撓度隨行駛距離變化的曲線(動撓度)。計算的結果中提取相應的最大靜撓度和最大動撓度,同時減去橋梁自重產生的撓度,即可得到汽車荷載最大靜撓度和最大動撓度,求取比值即為動力放大系數。本文中3個跨中位置處的4種荷載效應下的動力放大系數計算方法均相同。

3.2 車輛頻率對動力放大系數的影響

車輛模型的車體通過彈簧阻尼器與橋梁模型進行連接,車輛的振動頻率與車體的質量、彈簧阻尼器的剛度等有關,若改變車體的重量,不僅改變了車輛的頻率,也改變了車輛荷載的大小,不能獨立研究單一因素對動力放大系數的影響。本文取車體質量為30 t,分別取彈簧阻尼器的剛度為1×105、2×105、3×105、4×105

圖6 中跨跨中動靜撓度曲線Fig.6 Dynamic and static deflection curve of midspan

、5×105N/mm,即可計算得出相應車輛的振動頻率分別為2.906、4.109、5.033、5.812、6.498 s-1。故通過改變車輛的彈簧阻尼器的剛度,來改變車輛頻率,從而得到不同跨中位置處多種荷載響應的動力放大系數變化規律,分析結果如圖7—圖9所示。

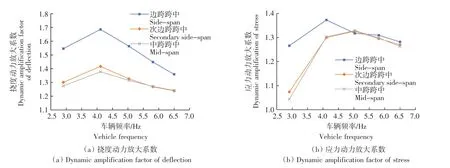
圖7 車輛頻率對中梁動力放大系數的影響Fig.7 Influence of vehicle frequency on dynamic amplification factor of center beam

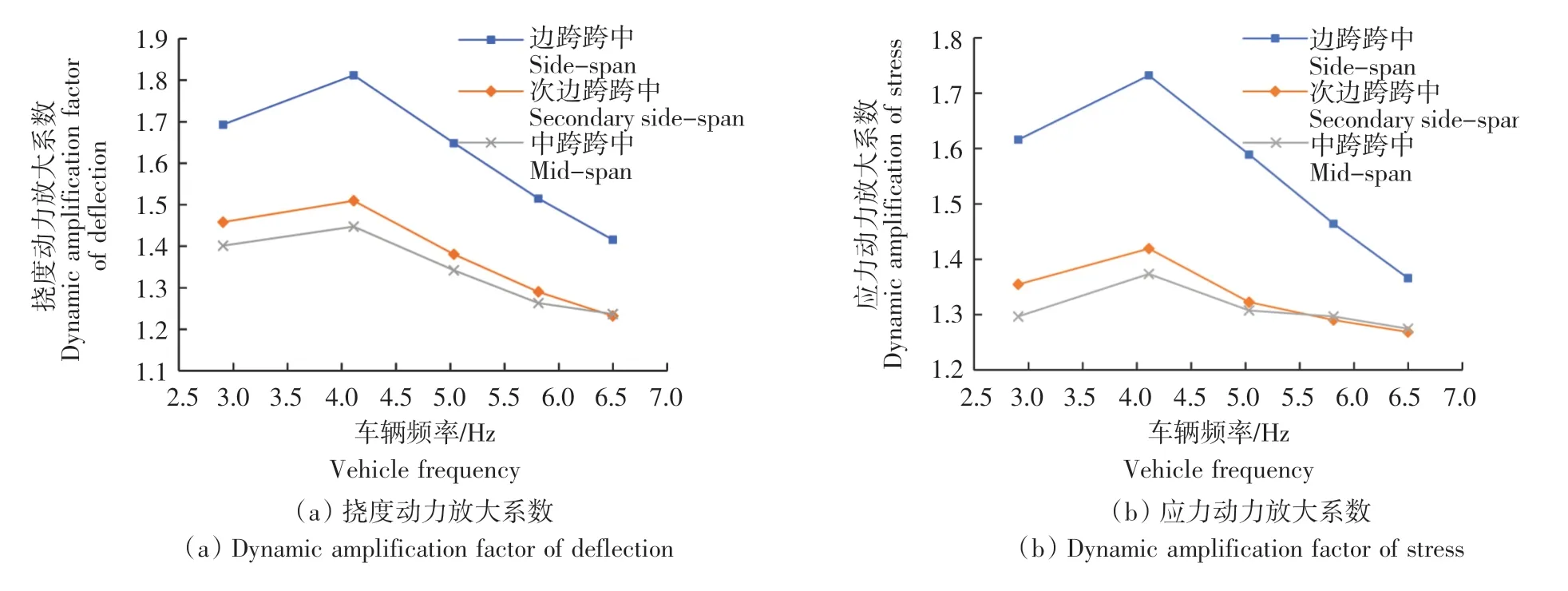
圖8 車輛頻率對次邊梁動力放大系數的影響Fig.8 Influence of vehicle frequency on dynamic amplification factor of secondary side beam

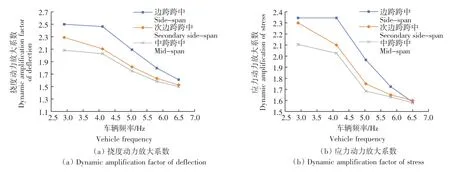
圖9 車輛頻率對邊梁動力放大系數的影響Fig.9 Influence of vehicle frequency on dynamic amplification factor of side beam

由圖7—圖9可知,中梁和次邊梁在不同的跨中位置,不同的荷載效應下得到的動力放大系數均在車輛頻率為4～5 Hz時取得最大值,經模態分析可得,橋梁頻率為4.44 Hz,此時車輛頻率與橋梁頻率十分接近,顯然車橋間產生的共振效應是此時產生最大動力放大系數的原因。然而計算所得邊梁處的動力放大系數卻隨著車輛頻率的遞增呈現衰減的趨勢,且沖擊系數的計算結果在車輛頻率較小時取值較大,能達到接近2.5的撓度沖擊系數。其次,對于所有的T形梁而言,在大多數情況下,邊跨跨中產生的動力放大系數均大于中跨跨中和次邊跨跨中,而中跨跨中和次邊跨跨中的動力放大系數則大小接近,尤其當車輛頻率較大時,3個不同跨中位置處的動力放大系數大小均較為接近。

3.3 橋梁頻率對動力放大系數的影響

由圖10—圖12可知,對于中梁而言,隨著橋梁頻率的增加,邊跨跨中在不同的荷載效應下得到的動力放大系數均在穩步下降,而次邊跨跨中和中跨跨中的動力放大系數則在撓度效應下先降后升,在應力效應下先升后降。而對于次邊梁而言,隨著橋梁頻率的增加,邊跨跨中在不同的荷載效應下得到的動力放大系數均在穩步下降,而次邊跨跨中和中跨跨中的動力放大系數則在撓度效應和應力效應下均呈現先降后升的趨勢。對于邊梁,其動力放大系數卻隨著車輛頻率的遞增呈現衰減的趨勢,且邊梁處的動力放大系數相比于中梁和次邊梁明顯較大。同時,也可看出3個不同跨中位置的動力放大系數值均隨著橋梁頻率的增加而更加接近。且對于不同的荷載效應下,跨中撓度動力放大系數能取最大值,均遠大于應力效應下的動力放大系數。

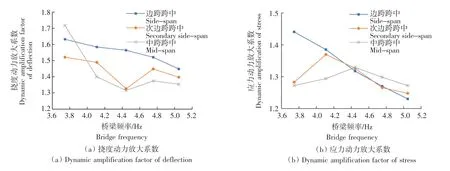
圖10 橋梁頻率對中梁動力放大系數的影響Fig.10 Influence of bridge frequency on dynamic amplification factor of center beam

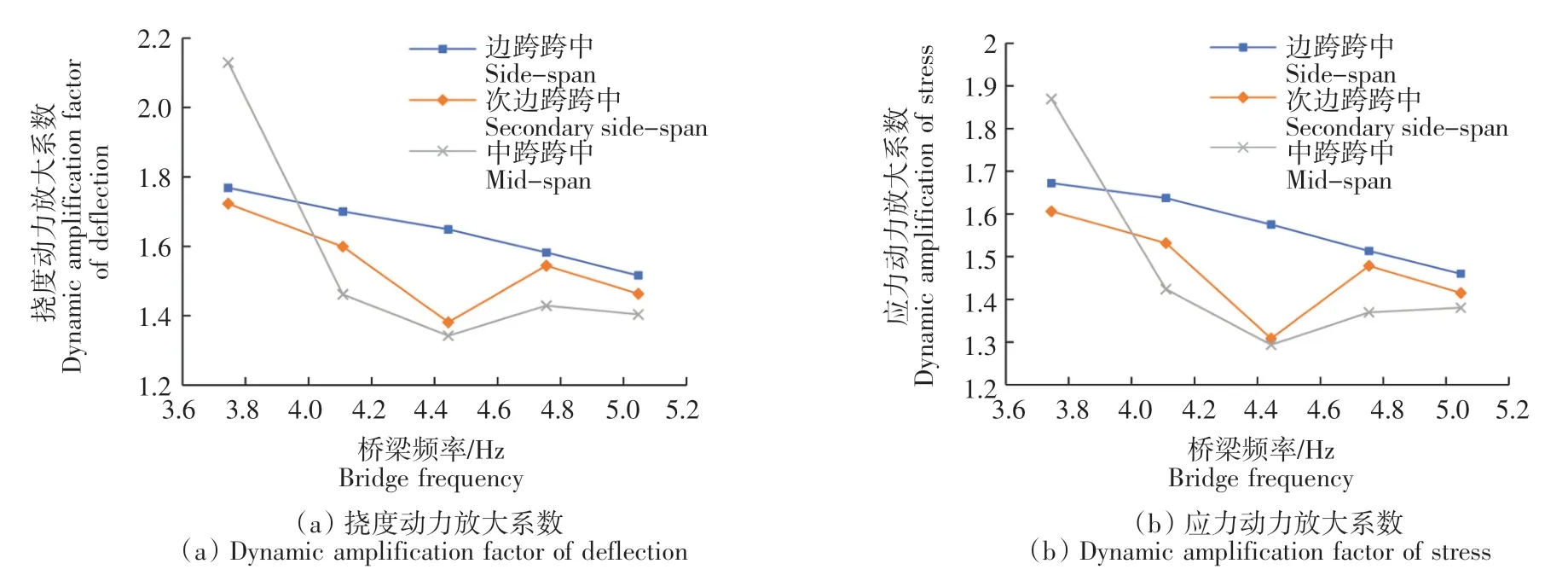
圖11 橋梁頻率對次邊梁動力放大系數的影響Fig.11 Influence of bridge frequency on dynamic amplification factor of secondary side beam

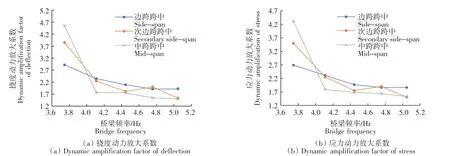
圖12 橋梁頻率對邊梁撓度動力放大系數的影響Fig.12 Influence of bridge frequency on deflection dynamic amplification factor of side beam

3.4 擾動頻率與橋梁頻率比值對動力放大系數的影響

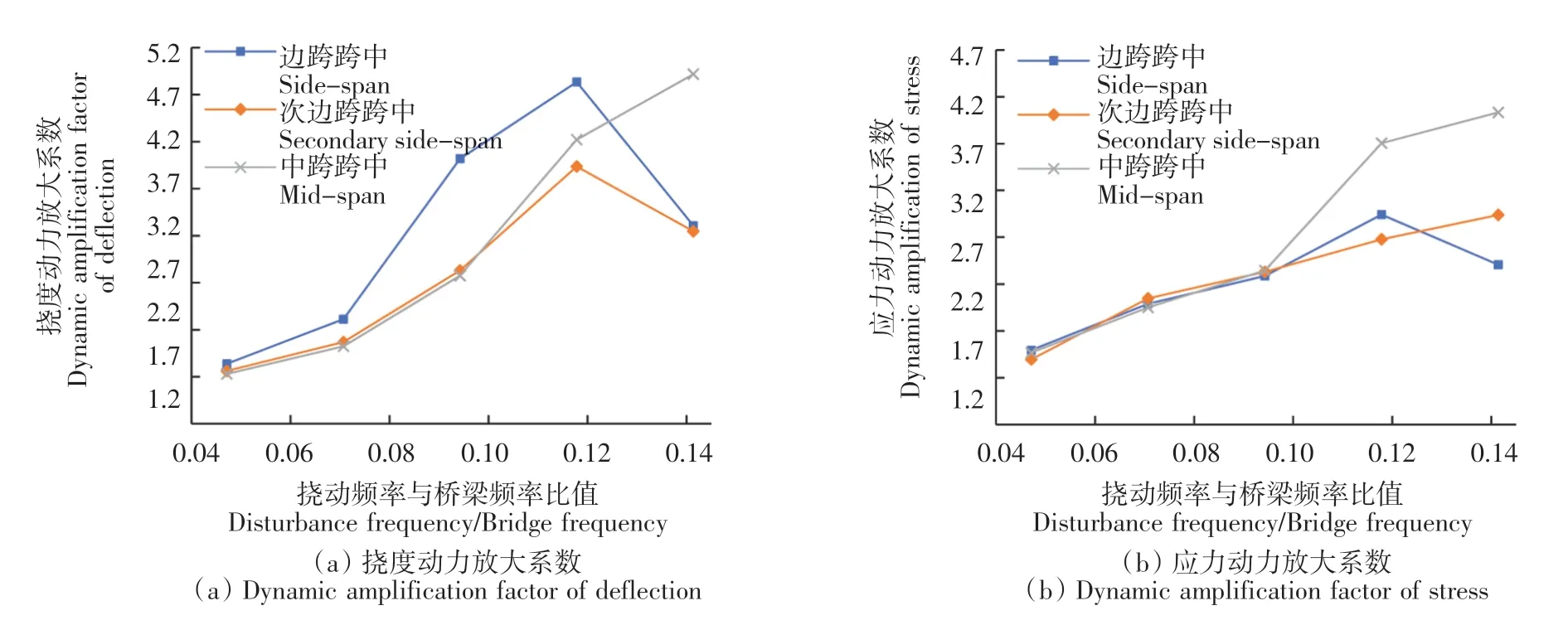
圖13 擾動頻率與橋梁頻率比值對中梁動力放大系數的影響Fig.13 Influence of disturbance frequency/bridge frequency on dynamic amplification factor of center beam

車輛對橋梁的擾動頻率與車輛行駛速度和橋梁的跨徑有關,同理,為了不影響中國公路通用圖中的橋梁標準結構,此處通過改變車輛的行駛速度來研究動力放大系數隨擾動頻率與橋梁頻率的比值變化的變化規律,所使用的行車速度分別為10、15、20、25、30 m/s,計算所得的擾動頻率與橋梁頻率比值分別為0.047、0.071、0.094、0.118、0.141,動力放大系數分析計算結果如圖13—圖15所示。

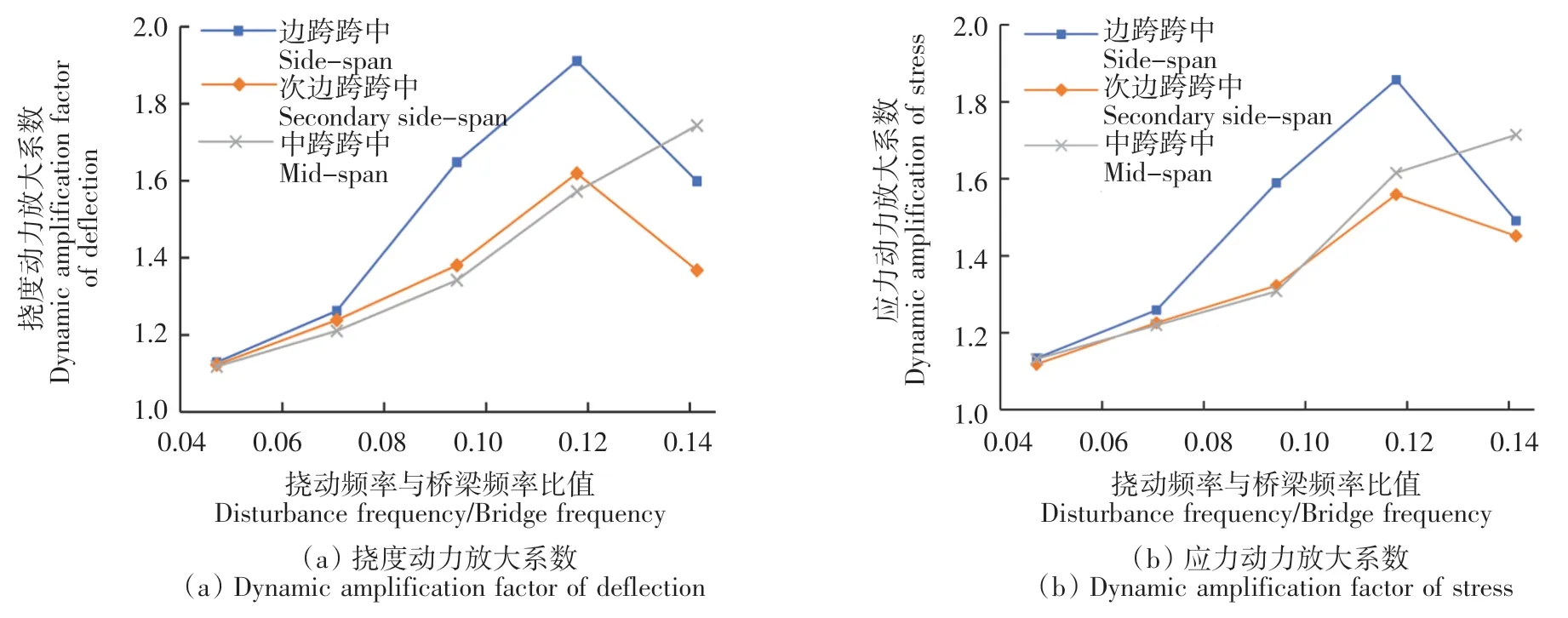
圖14 擾動頻率與橋梁頻率比值對次邊梁動力放大系數的影響Fig.14 Influence of disturbance frequency/bridge frequency on dynamic amplification factor of secondary side beam

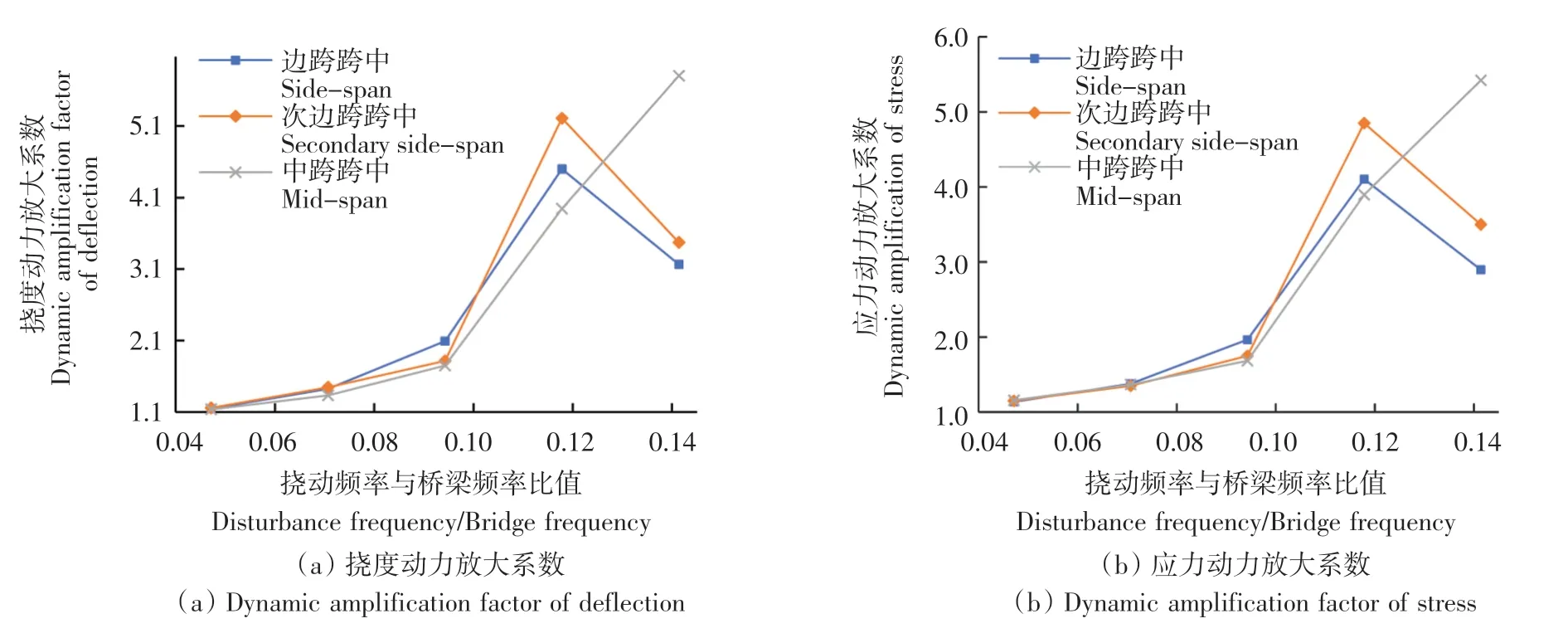
圖15 擾動頻率與橋梁頻率比值對邊梁動力放大系數的影響Fig.15 Influence of disturbance frequency/bridge frequency on dynamic amplification factor of side beam

由圖13—圖15可知,對于所有的T形梁而言,隨著擾動頻率與橋梁頻率比值(行車速度)的增加,邊跨跨中和次邊跨跨中在不同的荷載效應下得到的動力放大系數均為先升后降,且均在行車速度為25 m/s左右時達到頂點,而中跨跨中的動力放大系數則在不同的荷載效應下均為緩慢上升。同時,也可看出3個不同跨中位置的動力放大系數值均在車速較小時十分接近,隨著車速的增加而產生相對的差異。邊梁計算所得的動力放大系數雖變化趨勢與中梁和次邊梁相近,但邊梁的動力放大系數取值卻均遠大于中梁和次邊梁,最大的動力放大系數可達到5.8。

4 結論

車輛橋面行駛產生的動力響應有多種表現形式,本文基于車橋耦合振動理論,對車輛荷載作用下,多跨連續梁橋不同位置處撓度、應力2個動力響應的動力放大系數進行影響因素分析,得到的主要結論如下。

(1)當車輛頻率與橋梁的基頻接近時,將會產生共振的效果,此時在邊跨跨中、次邊跨跨中和中跨跨中等位置均會產生較大的動力放大系數。

(2)在不同的影響因素作用下,不同的荷載效應計算,所得的中跨跨中位置和次邊跨跨中位置處動力放大系數變化規律和數值大小均較為接近,而與邊跨跨中位置處的動力放大系數則存在一定的差異,說明邊跨處一端簡支的結構對此處的動力放大系數存在較大的影響。

(3)通過對橋梁多片主梁的動力放大系數進行分析,可以看出橋梁的邊梁相對于其中梁和次邊梁存在較大的差異,如邊梁的動力放大系數隨車輛頻率的變化趨勢與中梁和次邊梁明顯存在差異;邊梁的動力放大系數數值大小相較于中梁和次邊梁取值較大。

(4)本文有限元分析可以看出,車輛荷載不同響應的動力放大系數大小與變化規律均存在差異,且車輛頻率、橋梁頻率、行車擾動頻率等均對動力放大系數產生影響,故公路橋梁規范中的沖擊系數僅作為橋梁基頻的函數,與實際有較大的差距,有待改進。