核心素養視角下數學主題情境活動設計與思考
——以“向量的減法運算”為例*

徐倪明 陳算榮

(揚州大學數學科學學院 225002)

1 引言

《普通高中數學課程標準(2017年版)》(簡稱《課標》)提出高中數學課程教學應以學生發展為本，將立德樹人作為根本任務．《課標》指出高中數學學習中學生應具有良好的數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析素養[1]8，那么核心素養如何扎根課堂就成了現今的研究熱點．根據PISA測試的經驗，可以將學生解決現實情境問題的能力作為核心素養的參考指標[2]．這表明在教學中可通過創設現實情境，在情境問題的解決過程中，落實學生數學核心素養的發展．向量是解決現實問題的重要知識載體，將向量的學習整合于現實情境不僅自然，而且能更好地彰顯其學習的價值．現以“向量的減法運算”一課為例，借助“情境問題設計框架[3](表1)”，對該課例進行主題情境下的問題設計與思考，并簡析數學核心素養在問題情境教學中的培養．

表1中“知識理解”型情境問題對應于《課標》中六個核心素養的水平一層次．例如，數學抽象水平一層次意指“能夠在熟悉的情境中直接抽象出數學概念和規則，能夠在特例的基礎上歸納形成簡單的數學命題，能夠模仿學過的數學方法解決簡單問題．”[1]101這與表1中知識理解層次的內涵相一致．對于其他五個核心素養，在此不一一例舉．因為《課標》對每個核心素養的三水平劃分中都有對情境問題解決相應的水平層次描述，將其內涵對照可知，“知識遷移”型情境問題和“知識創新”型情境問題分別對應于《課標》中的六個核心素養的水平二層次和水平三層次．

表1 情境問題設計框架

2 教學設計片段

2.1 基于情境提出問題

問題1在某地的一條大河中，水流速度記為v0，擺渡船的自身航速記為v1，實際航速記為v2．根據這個情境，你能提出哪些數學問題？

圖1

設計意圖該情境問題取自前一節向量加法的例題，在已知水流速度v0和船的自身航速v1的情況下求船的實際航速v2，學生可根據實際意義直接構建向量加法模型(圖1)．改編為開放問題后，學生需要關聯原問題情境中積累的知識基礎“v0+v1=v2”,結合解方程的相關知識“一個方程，三個未知數，知二求一”思考問題的提出．該情境問題在數學知識維度上，涉及的知識點較為單一，為一元一次方程知識的簡單、直接應用；在情境維度上是學生已經解決過的且較為熟悉的情境問題，情境中三個速度的數學關系較為明顯，即方程中的“知二求一”，故屬于“知識理解”型情境問題．

教學導引在這個開放的情境問題中，學生能夠提出三個問題：

(1)已知水流速度v0與船的自身航速v1，求船的實際航速v2．

(2)已知水流速度v0與船的實際航速v2，求船的自身航速v1．

(3)已知船的自身航速v1與船的實際航速v2，求水流速度v0．

基于學生提出的這三個問題，教師引導學生研究三個問題求解的關系：問題(1)是學生熟知的求和向量的問題，而問題(2)和問題(3)是已知和向量與其中一個加向量，求另一個加向量的問題，這也是學生要學的新知．由此，通過問題(2)(3)，自然地引出向量減法運算的文字表述與字母表示，即求兩個向量的差的運算(x=a-b)．同時也為后續向量的減法運算探究作鋪墊，即關聯向量的加法運算法則．創設開放情境問題既復習了舊知“向量的加法”，同時也指向新知“向量的減法”．在此過程中，學生從熟悉的情境中直接提出數學問題，并抽象出向量加減運算式，有利于數學抽象素養(水平一)的培育．

2.2 關聯情境解決問題

問題2在某地的一條大河中，水流速度記為v0，擺渡船的自身航速記為v1，而擺渡船的實際航速記為v2．

圖2

(1)已知水流速度v0與船的自身航速v1(圖2)，求船的實際航速v2．

(2)已知水流速度v0與船的實際航速v2(圖3)，求船的自身航速v1．

圖3 圖4

(3)已知船的自身航速v1與船的實際航速v2(圖4)，求水流速度v0．

設計意圖承接問題1，圍繞學生提出的三個小問題，探究向量減法的運算法則，問題(1)幫助學生復習向量加法的平行四邊形法則和三角形法則，學生基于加法法則運用逆向思維可以解決問題(2)(3)．該情境問題在數學知識維度上，需要向量加法與向量減法多個知識點，且向量減法知識需要以向量加法知識為基礎探究得出；在情境維度上，(2)(3)是學生自主提出的新問題，問題的解決既需要應用逆運算關系，也需要運用向量的加法運算法則以及一些平面幾何知識，比如，已知平行四邊形的一條對角線和一條邊，如何畫出這個平行四邊形等，故屬于“知識遷移”型情境問題．

教學導引學生分別使用平行四邊形法則和三角形法則畫出問題(1)中的和向量v2(圖5、圖7)，教師快速檢測學生舊知的掌握情況，并做簡單復習．在解決問題(2)的過程中，基礎不牢的學生可能會無所適從，教師基于此給出提示：在問題(1)利用平行四邊形法則作和向量的過程中，v0，v1和v2最終構成了一個平行四邊形，v0和v1為平行四邊形的兩條邊，v2為平行四邊形的對角線(圖5)．學生關聯問題(1)(2)，可以發現問題(2)中的v0，v1和v2也可以構成一個平行四邊形(圖6)，且與問題(1)中的圖形為全等圖形．此時就將已知v0，v2求解v1的問題轉化為已知一個平行四邊形的一邊和對角線，求另一條邊的問題．在上述過程中，學生可以得到兩向量共起點時，差向量的作法——向量減法的平行四邊形法則，即以被減向量為對角線，減向量為邊構造平行四邊形，差向量為另一邊所在的有向線段．

圖5 圖6

再以問題(1)中的三角形法則為基礎，引導學生探究問題(2)向量減法的三角形法則(圖7)．學生有了平行四邊形法則的探究經驗，不難發現問題(1)(2)中的v0，v1和v2可以構成兩個全等的三角形(圖7與圖8)，此時的v0，v1和v2為三角形的三條邊，最終又轉化為“知二求一”的問題．在上述過程中，學生可以得到兩向量共起點時，差向量的另一種作法——向量減法的三角形法則，即以被減向量和減向量為邊構造三角形，差向量為減向量終點指向被減向量終點的向量．

圖7 圖8

探究活動結束，教師指出向量減法的三角形法則也是向量減法的幾何意義，并由學生進行自主歸納，教師完善補充：將a和b共起點時，a-b可以表示從b的終點指向a的終點的向量．在此過程中，學生能夠利用關聯的情境提出問題，通過關聯向量的加法運算法則，找到同起點情況下作差向量的兩種方法，并歸納總結出向量減法的幾何意義，有利于邏輯推理素養(水平二)的培育．

2.3 變化情境深入挖掘

變式1 在某地的一條大河中，水流速度記為v0，擺渡船的實際航速記為v2(|v2|>|v0|)，若此時的船順流(圖9)或者逆流(圖10)航行，請畫出船的自身航速v1．

圖9 圖10

設計意圖該情境問題是對問題2第(2)問的特殊化，目的是檢驗通過探究得到的兩向量共起點時差向量的兩種作法的適用性，鞏固學生對兩種方法的掌握．學生動手操作后可以發現兩種情形均無法構建平行四邊形，體會平行四邊形法則的局限性．而這兩種情形雖然也無法構造三角形，但是可以根據三角形法則所蘊含的向量減法的幾何意義求解問題(圖11、圖12)，這也體現了三角形法則的適用范圍更為廣泛．在數學知識維度上，該情境問題是對向量減法中差向量作法的簡單應用；在情境維度上，該情境問題是對問題2的特殊化，問題中三個速度的數學關系也較為明顯，故屬于“知識理解”型情境問題．

圖11 圖12

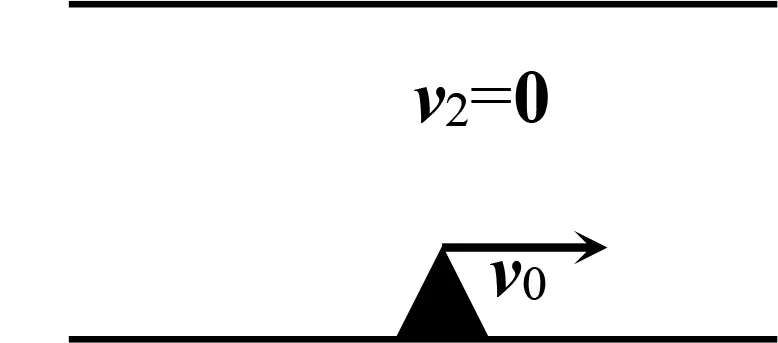
圖13

變式1′ 在某地的一條大河中，水流速度記為v0，擺渡船的實際航速記為v2，v2=0，即此時的船與水面保持相對靜止(圖13)，請畫出此時船的自身航速v1，并觀察v1和v0的關系．

設計意圖該問題是對變式1的特殊化，此時的被減向量為零向量，學生仍可以利用三角形法則快速地作出差向量v1．

引導學生觀察v1和v0之間的關系，得出v1和v0方向相反、大小相等(圖14與圖15)，從而自主生成相反向量的定義：與向量a長度相等、方向相反的向量，叫做a的相反向量，記作-a．因此v0和v1互為相反向量，為之后用相反向量定義向量的減法作鋪墊．在數學知識維度上，該情境問題涉及了新概念“相反向量”的生成，并要求學生通過探究，提出新的“向量的減法”的定義，屬于“知識創新”層面；在情境維度上，該情境問題是對變式1的特殊化，仍是學生熟悉的渡船情境，屬于“知識理解”層面．這也說明并非每一道情境問題的兩個維度都必須在同一水平．

圖14 圖15

教學導引學生根據題意作出v1,比較容易總結出v1和v0方向相反、大小相等，得到相反向量的概念．接著引導學生利用“相反向量”探究新的向量減法的定義．學生根據向量減法的字母表示得到v1=0-v0，根據向量的加法有v1=0+v1，所以有0-v0=0+v1，而v0和v1又互為相反向量，在上述的列式推導過程中，得出結論：零向量減去一個向量等于零向量加上這個向量的相反向量．教師引導學生猜想，并利用之前的例題探究這一結論推廣到任意向量是否適用，并得出結論：a減去b等于a加上b的相反向量．從而利用相反向量定義向量的減法：向量a加上b的相反向量，叫做a與b的差，即a-b=a+(-b)，求兩個向量差的運算叫做向量的減法．學生根據這一定義方法又得到了一種新的作差向量的方法，即利用相反向量與向量的加法法則．在此過程中，對學生的抽象和推理能力要求較高，學生通過特殊到一般的探究，利用相反向量定義向量的減法，有利于數學抽象素養(水平一)和邏輯推理素養(水平三)的培育．

3 總結與思考

核心素養視角下的課堂教學，要求教師重視情境問題的教學模式，這也是當前新課改的重要方向．問題是數學的心臟，思考是數學活動的主線[4]，實際的情境問題能調動學生的學習興趣，使學生體會到數學學習的必要性．[5]在本課例中，通過設置渡船主題情境，巧妙地將抽象的向量知識具體化、實際化，始終貫徹在解決情境問題的過程中生成知識的理念，幫助學生掌握向量的減法運算，得到多種作差向量的方法，同時還培養了學生的直觀想象、數學抽象、邏輯推理等核心素養．由于向量知識本身與現實情境的聯系非常密切，也只有在解決實際問題時，向量的價值才會最大化．圍繞知識理解、知識遷移和知識創新三個層次創設主題情境下的問題串，引導學生獨立思考、主動探究、合作交流，探求解決問題的方法,實現動眼、動手、動腦有機結合．鼓勵學生創新思考，加強數學實踐，發展學生的理性思維，同時注重培養學生良好的數學學習習慣[6]．

值得注意的是，主題情境與問題串都不是憑空產生的，其創設也要遵循諸多原則[7]，例如，(1)“數學關聯性”原則，杜絕為設置情境而設置情境，本課例中的渡船情境與向量問題關系緊密，情境中的“數學味”濃厚，所有問題的答案均與情境問題相關聯；(2)“貼近學生現實”原則，與學生的認知相匹配，本課例中使用學生熟悉的渡船問題作為主題情境貫穿教學，是基于學生視角的情境問題設置；(3)“整體性原則”，發揮主題情境的多維作用，本課例通過渡船這一主題情境的問題串設置，完成了多方面的教學任務(向量的減法運算、向量的減法作圖、相反向量的定義)，利用渡船情境的多維作用共同激發學生的學習興趣．

最后，在情境創設完成后，教師還要不斷地引導學生，使學生真正進入情境問題，在此過程中發展學生的數學核心素養，真正地讓學生做到會用數學的眼光觀察世界、會用數學的思維思考世界、會用數學的語言表達世界[8]．