張量積型Said-Ball 曲面的預處理漸近迭代逼近法

全浩榮，劉成志，李軍成，楊煉，胡麗娟

（湖南人文科技學院數學與金融學院，湖南婁底 417000）

在計算機輔助幾何設計中，數據插值是一項重要的內容。傳統的數據插值方法需要求解線性方程組，即配置方程。通常，線性方程組的系數矩陣是病態的，需研究高效的求解算法。為此，對配置方程的求解算法進行了研究并取得了不少成果，如基于Neville 消元的直接法［1-3］、基于矩陣分裂的迭代法［4-6］、子空間迭代法［7］等。近年來出現了一種具有幾何意義的迭代算法——漸近迭代逼近（progressive iterative approximation，PIA）法。由于PIA 法具有穩定的收斂性、在迭代過程中易修改幾何約束條件等優點而備受關注［8-9］。PIA 法最早源于齊東旭等［10］提出的盈虧修正思想。LIN等［11］證明了所有規范的全正基函數曲線（曲面）均具盈虧修正性質，并稱之為PIA 性質。

雖然PIA 法已有許多成果，但由于其收斂速度慢，在相關應用領域難以發揮優勢。近年來，PIA的加速方法研究逐漸成為幾何計算中的熱點。如加權PIA［12］（weighted progressive iterative approximation，WPIA）法、帶互異權值的PIA法［13-15］、Chebyshev 多項式加速迭代法［16］、帶形狀參數曲線的PIA法［17］等。由于PIA法等價于求解配置方程的Richardson 迭代法［6-7］，文獻［18］利用預處理技術對全正基函數的PIA 法進行預處理，得到收斂速度有明顯提升的預處理PIA（preconditioned progressive iterative approximation，

PPIA）法。隨后，文獻［19］結合矩陣Kronecker 積的性質將預處理技術應用于張量積型Bézier曲面的PIA法。

預處理技術的引入雖然能通過改善配置矩陣的譜分布提高迭代法的收斂速度，但在迭代過程中需額外求解預處理子的逆矩陣，增加了計算量，影響數據插值的計算效率。為進一步降低預處理技術的計算量，文獻［18-19］用經典的共軛梯度法近似求解預處理方程的法方程，即PPIA的非精確求解方法（inexact preconditioned progressive iterative approximation，IPPIA），但在求解過程中需在預處理方程兩邊同時乘以一個預處理矩陣的轉置矩陣，顯然，該法方程的條件數將隨之增大，影響求解預處理方程算法的計算效率、計算精度和穩定性。如果能找到一種合適的算法直接求解預處理方程而不是其法方程，則可提升計算效率。但由于預處理方程的系數矩陣是非對稱的，無法用共軛梯度法求解。文獻［7］利用廣義極小殘差法（generalized minimal residual method，GMRES）求解配置方程，得到插值曲線，數值實例表明，當插值點較少時，GMRES 法的計算效率很高，但當插值點較多時，得到的插值曲線精度不理想［18］。欣慰的是，非精確求解方法對精度的要求并不高，因此，本文將利用GMRES 法求解預處理方程，以進一步提升算法的計算效率和計算精度。

基于上述分析，本文在文獻［18-19］基礎上，研究張量積型Said-Ball 曲面的PPIA 法及其非精確求解方法，以期進一步提高數據插值的計算效率。

1 相關工作

1.1 張量積型Said-Ball 曲面

Said-Ball 基函數及相應的張量積型Said-Ball曲面片的定義［20］為：

1.2 漸近迭代逼近法

則稱S(0)(u，v)具有PIA 性質［11］。文獻［11］證明了所有全正基函數曲線（曲面）均具PIA 性質。文獻［20］稱Said-Ball 基函數為全正基函數，從而張量積型Said-Ball 曲面也具有PIA 性質。

張量積型Said-Ball 曲面的PIA 性質意味著式（3）收斂于插值曲面S?(u，v)的控制頂點，即

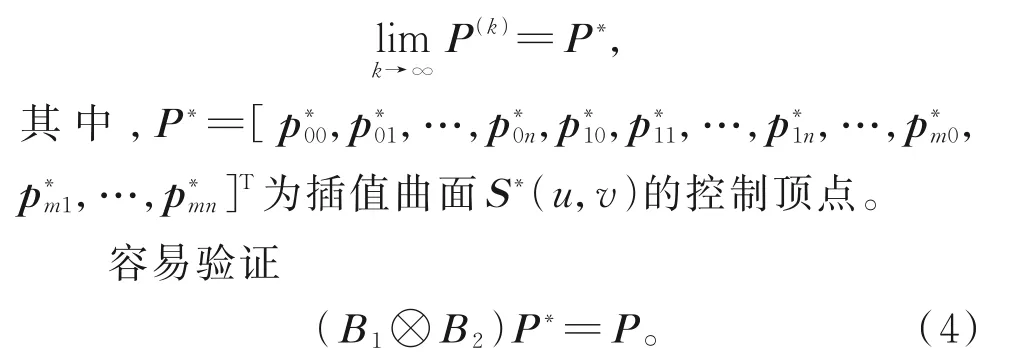
文獻［6-7］指出，PIA 法中式（3）也可看作求解式（4）的Richardson 迭代法。

最后，給出矩陣的Kronecker 積的性質［21］。

引理1關于矩陣的Kronecker積，有：

（a）A?B可逆當且僅當A和B均可逆，且有(A?B)?1=A?1?B?1；

（b）若A，B，C和D為階數滿足AC和BD乘法的矩陣，則(A?B)(C?D)=(AC)?(BD)。

2 預處理漸近迭代逼近法

文獻［18］利用對角補償約化技術構造了預處理子，該預處理子能在很大程度上改善全正基函數（包括Bernstein 基函數和Said-Ball 基函數）所生成的配置矩陣的譜分布。文獻［19］利用上述預處理子給出了張量積型Bézier 曲面的PPIA法，并取得了理想的加速效果。本文將該預處理技術應用于張量積型Said-Ball 曲面，得到張量積型Said-Ball 曲面的PPIA 法。

2.1 預處理子M1和M2的構造

首先，將配置矩陣B1分裂為

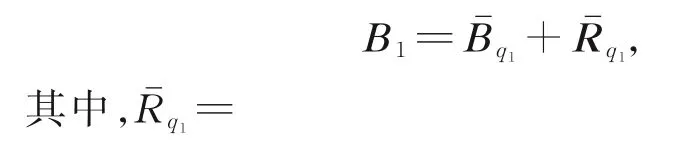
注1設M1和M2分別為對角補償約化技術所定義的關于B1和B2的預處理矩陣，相應的半帶寬分別為q1和q2，則有［18］：

（a）預處理子M1和M2均為可逆矩陣。

（b）對于i=1，2，經預處理后的矩陣的譜隨半帶寬qi的增大向1 附近聚集。

（c）綜合考慮計算量和預處理效果，當預處理子的半帶寬約為配置矩陣階數的一半時效果較好。

2.2 預處理方法

在得到預處理子M1和M2后，由引理1，對式（4）進行預處理，有

注2文獻［19］指出，在構造張量積型曲面的PPIA 法時，用矩陣的Kronecker積的性質分別對配置矩陣B1和B2進行預處理，具有充分發揮預處理子的預處理效果和提高算法的穩定性和魯棒性的作用。

3 PPIA 法的非精確求解方法

由式（6），在PPIA 法的迭代過程中需計算

與式（3）相比，這顯然增加了額外計算量。因矩陣的求逆運算計算量較大，且具有不穩定性。當n和m均較小時，式（7）很容易計算，但當n和m較大時，式（7）的計算復雜度增大，穩定性也隨之降低，從而影響PPIA 法的計算效率。

注意到，計算式（7）等價于求解線性方程組

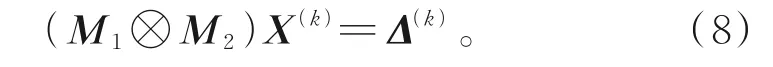
考慮用迭代法求解式（8），會得到一個嵌套迭代格式。將式（6）看作外迭代格式、將求解式（8）的迭代法看作內迭代格式，若對內迭代的精度要求較高，則求解式（8）需花費較多的計算時間。在不影響外迭代收斂性的前提下，降低內迭代的精度，可減少內迭代的計算時間，從而提高計算效率。因此，為減少計算量和提高算法的穩定性，考慮用GMRES 法求解式（8），得到的近似解。

其中，τk為給定的迭代終止誤差閾值，‖?‖F為Frobenius 范數。

于是可得到下一步迭代的控制頂點

稱式（11）為張量積型Said-Ball 曲面預處理漸近迭代逼近法的非精確公式，記為IPPIA-GMRES。

為提高計算效率，當

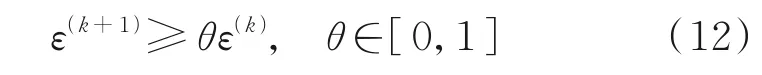
時，式（11）終止迭代，其中ε(k)為IPPIA-GMRES 法迭代k次所生成的近似插值Said-Ball 曲面的插值誤差，

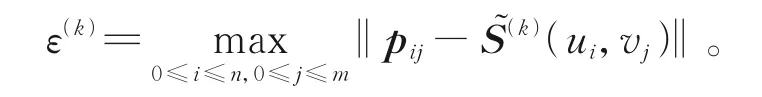
現討論張量積型Said-Ball 曲面IPPIAGMRES 法的收斂性。為方便，下文的定理及證明中均將M1?M2記為M，將B1?B2記為B。

定理1設M1和M2分別為對角補償約化技術所定義的關于B1和B2的預處理矩陣，P?為Said-Ball 插值曲面的控制頂點。對于每個外迭代步k，利用GMRES 法求解式（9），得到式（7）的近似解X(l，k)，則對IPPIA-GMRES 法迭代所生成的序列，有

定理1 得證。

由定理1，對于給定的預處理子M1和M2，IPPIA-GMRES 法的收斂性主要由τk決定。顯然當τk=0時，利用GMRES 法可得到式（7）的精確解，此時IPPIA-GMRES 法退化為PPIA 法。因此，為使迭代法具有更好的收斂效果，τk越小越好。但τk越小，意味著對內迭代精度的要求增高，內迭代次數增加，計算量增大。在實際計算中，可在不影響外迭代收斂性的前提下降低對內迭代計算精度的要求（無需τk=0），以提高計算效率。

4 數值實例

文獻［12］指出，在最優權系數下，WPIA 法比PIA 法具有更快的收斂速度，因此本文將與最優權系數下的WPIA 法進行對比。文獻［7］利用GMRES 法求解曲線情形的配置方程，得到插值曲線，本文也將利用非重啟的GMRES 法求解曲面情形的配置方程，得到插值曲面。由于GMRES 法的收斂性取決于系數矩陣的譜分布和Ritz 值等，而本文提出的預處理子能改善配置矩陣的譜分布，因此本文的預處理技術也可用于GMRES法，即預處理 GMRES（preconditioned GMRES，PGMRES）法。

方便起見，在數值實例中，記文獻［19］的方法為IPPIA-CG。所有實驗均在Intel（R）Core（TM）i7-8565U CPU @ 1.80 GHz 1.99 GHz、內存為8 GB的筆記本電腦上實現。

例1 給定16個待插值的數據點：（1，1，1），（2，1，2），（3，1，2），（4，1，1），（1，2，2），（2，2，2.5），（3，2，2.5），（4，2，2），（2，3，2），（1，3，2），（2，3，2.5），（4，3，2），（1，4，1），（2，4，2），（3，4，2），（4，4，1）。

例2 給定20個數據點：（1，1，1），（1，2，4），（1，3，2），（1，4，2），（1，5，2），（2，1，2），（2，2，2），（2，3，3），（2，4，6），（2，5，4），（3，1，3），（3，2，2），（3，3，4），（3，4，4），（3，5，3），（4，1，4），（4，2，6），（4，3，1），（4，4，1），（4，5，2）。

例3 逼近從函數

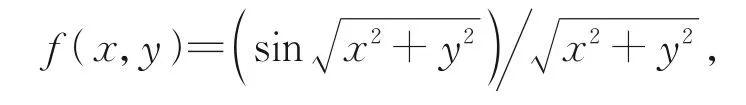
上采樣得到11×12個數據點：

例4逼近從函數

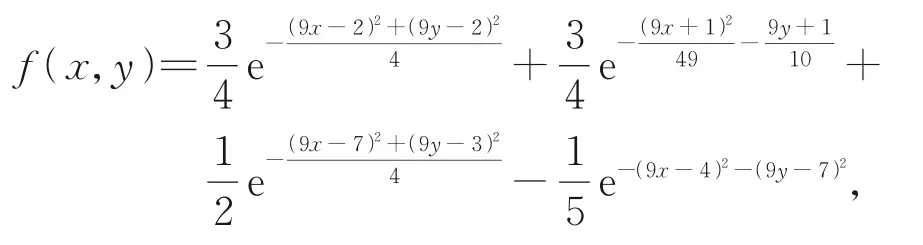
上采樣得到42×54個數據點：

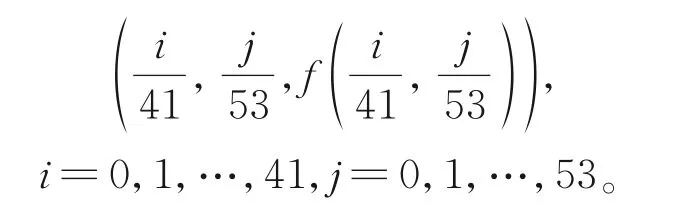
實驗參數選取如下：由注1，在利用PGMRES、PPIA 和IPPIA-GMRES 法逼近例1～例4 中數據點時，預處理子的半帶寬取值如表1 所示。在測試IPPIA-GMRES 法時，取式（10）中的τk=0.01，取式（12）中的θ=0.85。為方便比較，取IPPIA-CG 法中的τk=0.01，θ=0.85。

表1 例1～例4 中預處理子的半帶寬Table 1 Half-bandwidth of preconditioners in examples 1 to 4

在逼近例1～例3 數據點時，PIA、WPIA 和PPIA 法迭代矩陣的譜分布如圖1 所示，相應的迭代矩陣的譜半徑如表2 所示。可知，與PIA 法和WPIA 法相比，PPIA 法迭代矩陣的大部分特征值向0 方向聚集。PPIA 法迭代矩陣的譜半徑明顯小于PIA 法和WPIA 法。因為迭代矩陣的譜半徑越小，收斂速度越快，所以PPIA 法的收斂速度提升很快。此外，由于迭代矩陣的譜分布更聚集，P-GMRES 法的收斂效果也得到了改善。

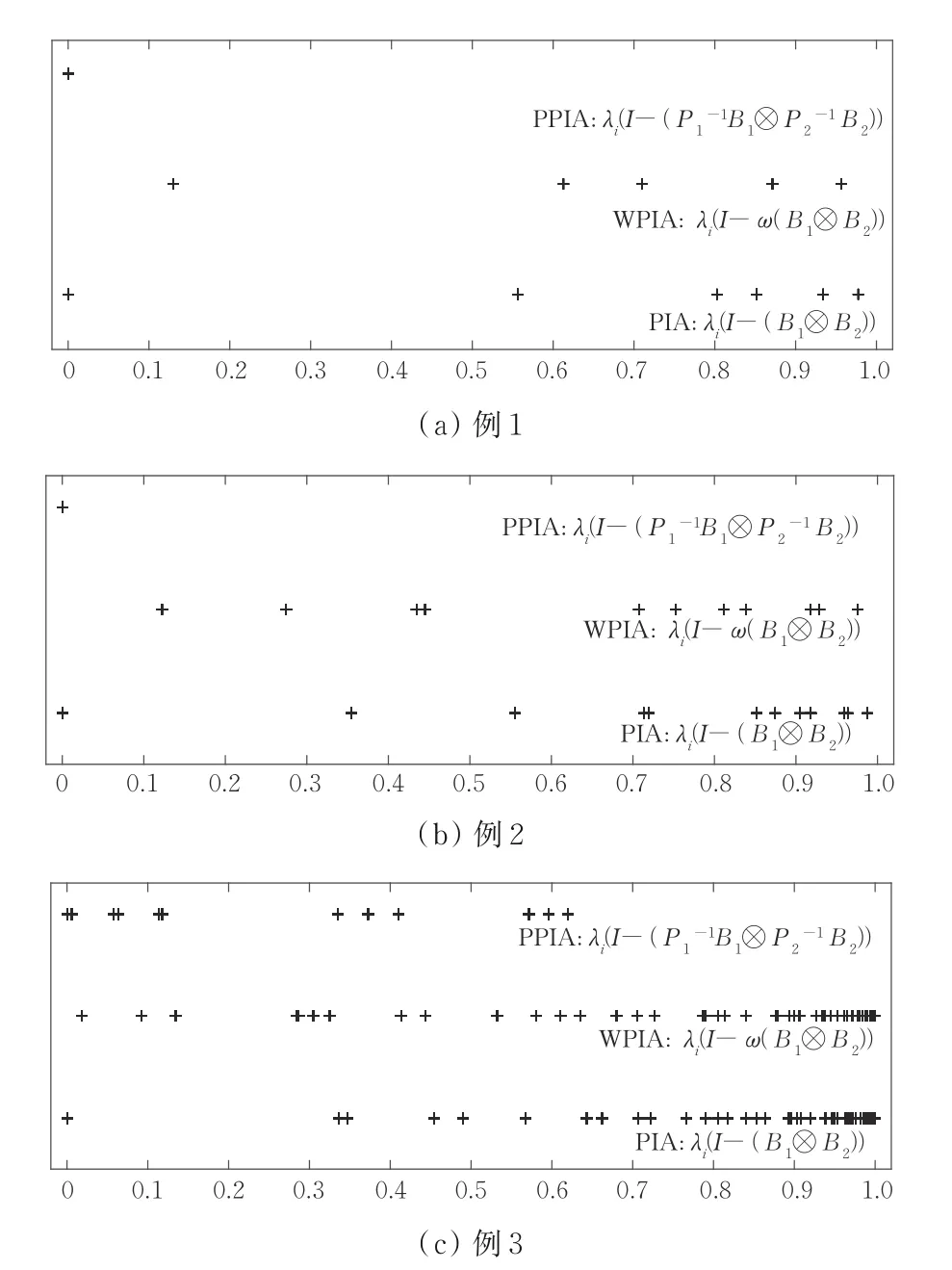
圖1 例1～例3 中PIA、WPIA 和PPIA 法迭代矩陣的譜分布Fig.1 Spectral distributions of iteration matrices of PIA，WPIA and PPIA in examples 1 to 3

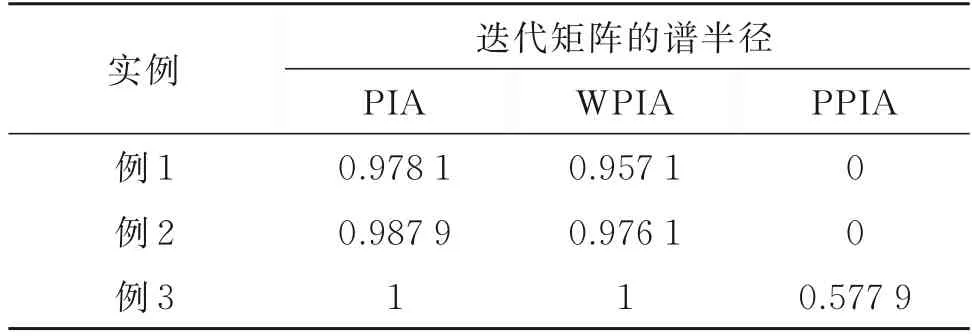
表2 例1～例3 中迭代矩陣的譜半徑Table 2 Spectral radius of iteration matrices in examples 1 to 3

表3～表5 分別為用不同方法迭代逼近例1～例3 中數據點時的插值誤差ε和運行時間T，可知，WPIA 法的收斂速度較慢，PPIA 法的收斂速度較快，特別是例1 和例2，用PPIA 法迭代一次就能達到機器精度。同樣，在數據點很少時，用GMRES法和P-GMRES 法均能得到精確的插值曲面；隨著數據點的增多，2 種方法的插值誤差隨之減小，PGMRES 法比GMRES 法減小更明顯，說明本文提出的預處理子能改善GMRES 法的收斂性。在插值誤差幾乎相同的情況下，PPIA 法在迭代次數k和運行時間上具有優勢，說明本文方法具有計算效率優勢。

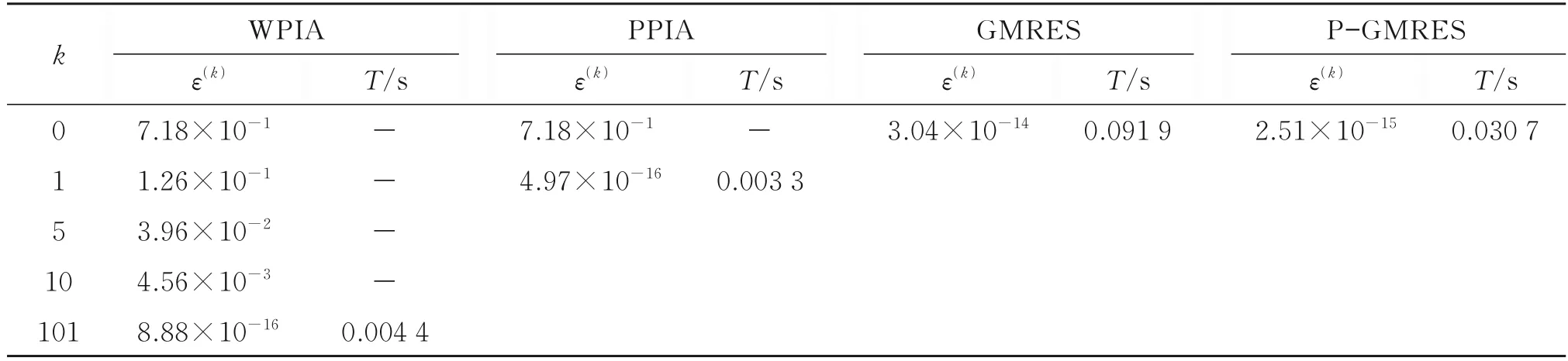
表3 例1 中WPIA、PPIA、GMRES 和P-GMRES 法的插值誤差和運行時間Table 3 Interpolation errors and runtime of WPIA，PPIA，GMRES and P-GMRES in example 1

表4 例2 中WPIA、PPIA、GMRES 和P-GMRES 法的插值誤差和運行時間Table 4 Interpolation errors and runtime of WPIA，PPIA，GMRES and P-GMRES in example 2

表5 例3 中WPIA、PPIA、GMRES 和P-GMRES 法的插值誤差和運行時間Table 5 Interpolation errors and runtime of WPIA，PPIA，GMRES and P-GMRES in example 3

在逼近例4 中數據點時，由于數據點較多，WPIA 法的收斂速度很慢，PPIA 法得到的插值誤差較大，這由預處理子的求逆運算不穩定造成。此時GMRES 法和P-GMRES 法的運算結果亦不理想，可考慮采用非精確求解方法近似求解預處理方程。由表6的數值結果知，在終止閾值θ相同時，IPPIA-CG 法只需迭代1 次（此時，可通過提高內迭代精度增加迭代次數，以減少IPPIA-CG 法的插值誤差），IPPIA-GMRES 法需迭代6次，但插值精度也相應提高，說明IPPIA-GMRES 法能更有效地插值較大規模的數據點。在運行時間上，IPPIAGMRES 法雖不及GMRES法和P-GMRES法，但明顯優于WPIA法，且IPPIA-GMRES 法的插值誤差更小。

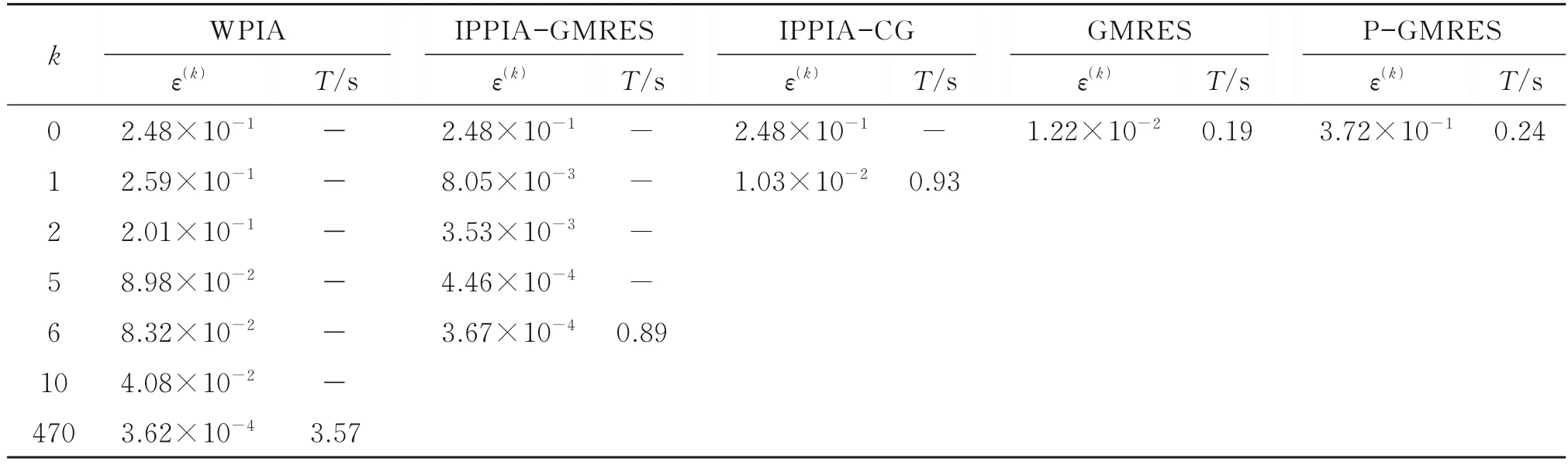
表6 例4 中IPPIA-GMRES 法和其他方法的插值誤差和運行時間Table 6 Interpolation errors and runtime of IPPIA-GMRES and the other methods in Example 4

用WPIA 法和PPIA 法迭代逼近例1～例3的數據點，得到的Said-Ball 曲面如圖2～圖4 所示；用WPIA、IPPIA-CG 和IPPIA-GMRES 法迭代逼近例4 中的數據點，得到的Said-Ball 曲面如圖5 所示。不難看出，由本文方法生成的張量積型Said-Ball 曲面能快速逼近給定數據點。

圖2 例1 中的Said-Ball 插值曲面Fig.2 Said-Ball interpolation patches in example 1

圖3 例2 中的Said-Ball 插值曲面Fig.3 Said-Ball interpolation patches in example 2

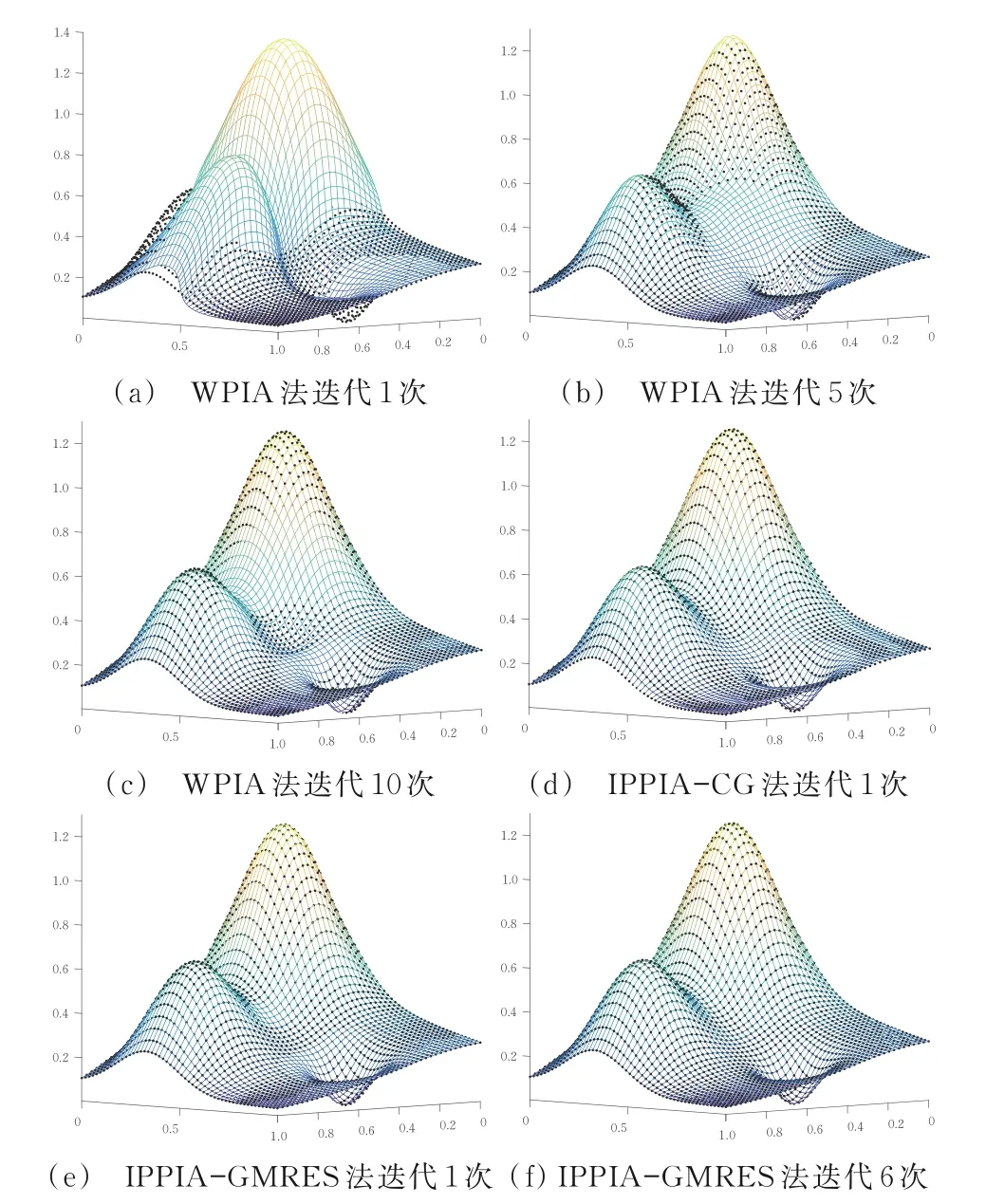
圖5 例4 中的Said-Ball 插值曲面Fig.5 Said-Ball interpolation patches in example 4

5 結論

基于對角補償約化技術，探討了求解張量積型Said-Ball 曲面的PPIA法，并用GMRES 法求解預處理方程，得到非精確解，即IPPIA-GMRES 法。相較文獻［18］利用共軛梯度法求解預處理方程的方法，本文的非精確求解方法計算量更小，得到的插值曲面精度更高，計算效率也更高。此外，由于本文提出的預處理方法能使配置矩陣的譜分布更集中，在處理規模適當的插值問題時，采用對角補償預處理子能在一定程度上改善GMRES 法的收斂性。

由于預處理技術能在有效改善非分段（片）基函數的同時配置矩陣的譜分布［19，22］，因此本文方法能推廣應用于類似曲面（如張量積型Bézier 曲面）PIA法的加速問題。但本文方法也存在局限性，由于分片曲面（如雙三次B 樣條曲面、NURBS 曲面等）PIA法中的配置矩陣為稀疏矩陣，利用對角補償約化技術構造的預處理子效果不明顯，甚至不起作用。不同于分片插值，本文方法利用一張Said-Ball 曲面對所有數據點插值，具有更高的連續性。未來，將進一步探討分片曲面PIA 法的加速問題。