基于生成對抗網絡的小樣本光伏發電短期預測

牛宇童，馮天波，李 慶，崔昊楊

(1.上海電力大學電子與信息工程學院，上海 200090；2.國網上海市電力公司信息通信公司，上海 200030；3.國網上海市電力公司閘北發電廠，上海 200432)

對于新建光伏電站而言，準確的光伏發電預測較為困難。目前較多發電量預測的深度學習方法往往依賴高質量海量數據[1]，然而新建電站氣象條件相關光伏發電量樣本數據積累不夠，從而使預測時效性和準確率難以保證[2]。此外，在數據傳輸損失和噪聲干擾的影響下，光伏發電量數據丟失(統計表明可達40%以上[3])或存在臟數據[3]的情況并不少見，造成可用數據樣本更為匱乏。在小樣本數據增強的相關研究中，肖等[4]提出基于GAN 數據生成模型和RCGAN 負荷預測模型的SLF 方法，對小樣本進行樣本擴充，所得結果具有良好的穩定性和準確性。Zhang 等[5]采用SolarGAN 方法補全缺失的光伏數據，誤差減少至23.9%。上述研究未考慮到GAN 算法本身也需要大量的原始數據來支持網絡的訓練收斂，若數據量較少，容易陷入模式崩塌和梯度爆炸。此外，目前小樣本光伏預測的方法由于未充分考慮氣象參數的影響權重，分析不充足，輸入不充分，所以依然存在一定的預測誤差[6]。對此，提出基于遷移學習改進WGAN 和LSTM 的小樣本光伏發電量短期預測方法。相較于文獻[5]中的傳統WGAN 模型，本文在此基礎上引入深度遷移學習，學習已有的源域數據集知識，并遷移至對缺失樣本的數據增強，生成與原始數據高度相似分布的樣本；將氣象參數根據與發電量的相關程度賦予不同權重作為輸入，在LSTM 方法中增加了誤差補償機制，進一步降低誤差。本文所提方法不僅解決了傳統人工神經網絡樣本不足的問題，提高了生成對抗網絡的泛化能力，同時有效提高了新建光伏電站小樣本情況下光伏發電量預測準確率。

1 小樣本數據增強與發電量預測模型構建

本文針對新建光伏電站小樣本光伏發電量短期預測分別構建了數據增強模型和光伏預測模型，技術路線如圖1 所示。引入深度遷移學習算法對模型微調(fine-tuning)，并以訓練參數優化后的WGAN 模型對目標數據集樣本進行高效擴充。在LSTM 預測中，通過對擴充數據中的氣象參數與發電量作相關性和可視化分析，按照相關性程度賦予不同的權重作為輸入數據，并采用相似氣象條件發電值對預測結果誤差進行補償，得到最終的預測結果。

圖1 小樣本光伏發電量短期預測的技術路線

1.1 數據增強模型構建

常規的GAN 模型由生成網絡G(generative network)和判別網絡D(discriminative network)構成，如圖2 所示。G 網絡由LSTM 模型構成，用以生成數據；D 網絡由CNN 模型構成，用以對生成數據和實際數據進行分類。同時交替訓練LSTM模型和CNN 模型：G 網絡學習光伏數據集的數據分布，D 網絡判別光伏數據來自實際樣本數據而不是生成樣本數據的概率。G 網絡的訓練過程是最大化D 網絡判別出錯的概率。G 和D 的博弈存在唯一解，當D 估計概率為1/2 時，G 完成高類似光伏樣本數據的生成過程。GAN 同時可反向傳播訓練，通過G 和D 的博弈即可完成對抗訓練過程。常規GAN 的目標函數如下[7]：

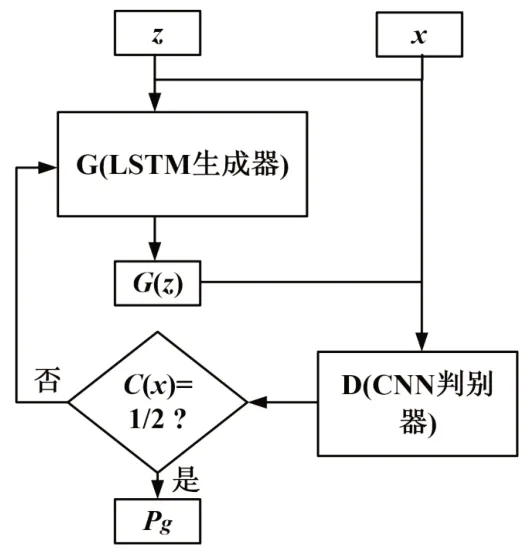
圖2 WGAN 結構

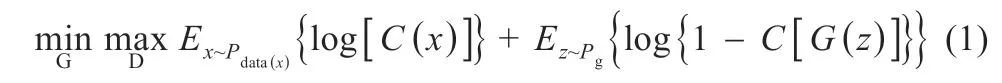
式中：Pdata為實際目標缺失數據集的樣本分布。

設輸入G 的天氣變量和光伏參數為z～Pz，G 網絡生成樣本G(z)的分布為Pg，D 網絡判別概率為C(x)。訓練D 以更準確地判別生成樣本和實際樣本，同時訓練G 以最小化C[G(z)]。常規GAN 使用JS 散度來衡量Pdata和Pg兩個概率分布的相似度，由于Pdata和Pg幾乎不重疊，無論兩者差異大小，JS 散度均為常數log2，并導致生成網絡梯度消失[8]。為解決該問題，利用Wasserstein 距離代替JS 散度對概率分布進行量化[9]：

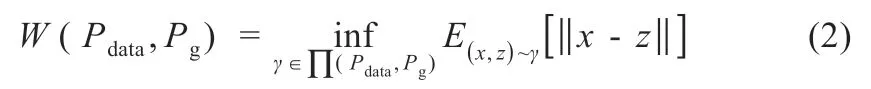
式中：∏(Pdata,Pg)為生成/實際光伏數據的聯合分布。對于任意聯合分布γ，取其中實際目標數據集光伏數據x和生成樣本數據z，計算出兩類樣本距離||x－z||，得到該聯合分布γ 下樣本的期望值，在所有可能的聯合分布中對該期望值取下限值。WGAN 的整體結構和訓練過程與常規GAN 一致。WGAN 整體訓練的目標函數為[5]：

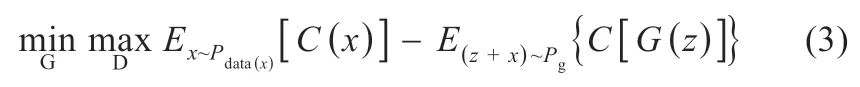
對于式(3)，將隨機噪聲和實際目標數據集的樣本即(z+x)同作為G 網絡的輸入。D 網絡應滿足1-Lipschitz 函數集的限制條件：

鑒于原始數據集樣本量不足難以訓練WGAN，使用預訓練的網絡來重新微調，遷移學習的流程如圖3 所示。先用源域數據集對WGAN 預訓練，得到初始化網絡參數，凍結訓練參數并對模型進行層遷移，保留除全連接層外的模型參數和權重；使用少量目標域數據訓練完整的新全連接層并對權重進行保存；采用層凍結的方法對部分關鍵層或整個模型的訓練參數進行微調。訓練完成后，遷移部分的權重參數對模型起到了優化效果，使得生成樣本更加接近實際樣本的分布。因此，將源域數據集內學到的知識用于指導生成網絡的迭代優化，完成源域內知識到目標域的遷移。

圖3 遷移學習流程

1.2 光伏預測模型構建

利用三層LSTM 對擴充的目標數據集進行預測。在三層LSTM 層中，第一層結構為32×20，32 是網絡輸入樣本數，20是樣本數據緯度。第二層為32×16，第三層為32×12，輸入層為1×32，輸出層為1×1。使用Relu 函數作為激活函數，采用Adam 算法對各層權值進行優化，設置Dropout 機制來避免過擬合。以此，LSTM 對時序數據進行建模，并且克服了RNN中的“梯度消失”和“梯度爆炸”問題，從而實現光伏序列數據預測[10]。

為減小氣象因素誤差，本文增加誤差修正環節。選取目標數據集中的現場溫度、光照強度等氣象數據構造特征向量，建立目標函數如下[11]：

目標函數需滿足以下條件：

式中：M為氣象數據集；V1，V2，V3…分別為溫度、光照強度等光伏氣象數據；ρx為相關系數，且ρ1+ρ2+ρ3+…=1；dij為各樣本點到V1，V2，V3…等光伏氣象數據的歐氏距離；為濾除氣象數據奇點數據和偶發因素，設定J*為最大可允許修正量，超出此范圍則修正無效。

在小樣本氣象數據庫中，搜索并比較與預測發電量值對應的氣象數據最相似的樣本，索引該組氣象數據對應的光伏發電量實際值Pc和預測值Pr，取Pc和Pr差值的絕對值對LSTM 的初步發電量預測值進行誤差補償，獲得最終發電量預測值，并將最終預測值實時上傳數據庫，以便進行下一次誤差補償時更加精確。計算公式如下[11]：

式中：Po為LSTM 神經網絡的初步發電量預測值。對分子取絕對值做限幅，意味著整體預測可能偏高。由于目標數據集中發電量最高值Pmax在10～12 之間，對于計算出高于Pmax的數值，直接取預測值進行截斷。

2 案例分析

實驗在CUDA8.0，Tesnoeflow1.4，Nvidia Titan1080ti GPU(12G)平臺下進行，以GEFCom2014 年太陽軌道的公開太陽數據集[12]為源域數據集，以2018 年DataFoutain 公開的光伏電站數據集作為目標數據集進行案例研究。使用均方誤差(MSE)、均方根誤差(RMSE)和歸一化均方根誤差(NRMSE)作為評價指標對模型精度進行評估。

2.1 數據增強結果

為評估無監督模型生成結果，設計了基于完整數據集生成小樣本數據集實驗。以DataFoutain 的光伏電站數據集為基礎，按照40%缺失率隨機刪除，生成目標缺失小樣本數據集；用數據增強模型補全缺失的40%數據，將生成的數據與實際數據進行比較。使用下式隨機刪除光伏電站數據集中的部分數據[5]：

式中：enj為光伏電站數據集中第j個樣本的向量表示；Mmj為光伏電站數據集中第j個樣本的0-1 矩陣，作內積處理。0 為缺失，1 則保留，從而生成40%缺失率的目標缺失數據集。使用式(2)～(4)構造WGAN 模型，訓練判別網絡時選擇優化函數RMSProp。同時，訓練生成網絡和判別網絡時選擇優化函數為Adam，對模型的參數進行更新[13]。設置Epoch 為30，Batchsize 為16。由于太陽數據集和光伏電站數據集并不完全相同，對其作領域自適應優化。對兩個數據集的數據進行二分類，盡可能篩選出太陽數據集中與光伏電站數據集特征分布相近的數據，因此，將基于太陽數據集特征訓練的判別網絡用于光伏電站數據集。對二分類時的損失函數進行優化來提高分類準確性，優化目標為[9]：

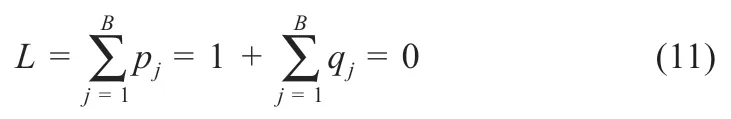
式中：pj=0 表示太陽數據集的數據標簽；qj=1 表示光伏電站數據集的標簽。得到分類后的太陽數據集后，利用前文的遷移學習流程對光伏電站數據集進行數據增強，得到目標擴充數據集。通過與原始目標數據集進行比較，可得擴充樣本和實際樣本的MSE為0.079，NRMSE為0.503。而以同樣本數據庫測試表明，SolarGAN 和GAN-Z 等常規模型的MSE分別為0.196 和0.369，因此本文方法生成的數據更符合實際數據分布。

2.2 數據預處理和可視化分析

對輸入數據進行有效預處理可減少訓練和計算代價并提高模型預測精度。本文對擴充后的光伏電站數據集進行了標準化處理，所有數據都在0～1 的特定范圍內重新縮放。擴充數據集每周期每天200 個ID，則45 d 訓練集數據量為9 000 條。對45 d 內的氣象和電壓電流等參數作散點圖，圖4(a)、(b)分別為平均功率和電壓的特征散點圖。發現平均功率和電壓等各特征參數基本都存在明顯異常值。根據統計學知識，異常值判定遵循以下基本規則：data∈[均值－3×標準差，均值+3×標準差]，凡是不在此范圍內的數據均作奇點數據進行刪除處理，并用上一點有效值替代。

圖4 目標數據集部分特征散點圖

為探明各特征參數變化對光伏發電量的影響，本文計算了各氣象和電壓電流等參數與發電量的Pearson 相關系數，公式如下[14]：

式中：X為各特征參數值；Y為光伏發電量值；總體相關系數ρ為X、Y之間的協方差和標準差乘積的比值。若其值越接近＋1 則相關性越密切，其值大于等于0.8 時，視為高度相關。各特征參數與發電量的Pearson 系數如表1 所示，根據相關性系數的大小對各特征參數賦予不同的權重。

表1 Pearson 系數結果

為使相關性直觀體現，本文對部分特征參數與發電量之間的變化關系數據進行了可視化處理。從圖5 中發現，圖5(a)、(b)分別為光照強度/40 和平均功率/480 的曲線，(a)、(b)中特征參數的變化曲線和發電量基本重合，光照強度和平均功率的Pearson 系數值也超過了0.8，所以其與發電量表現出較強相關性。圖5(c)為板溫的曲線，板溫的變化曲線與發電量只有小部分重合，Pearson 系數值為0.519，表現出中等強度相關性。圖5(d)為風速曲線，(d)中特征參數的變化曲線和發電量的重合較少，Pearson 系數值也只有0.128，表現出較弱相關性。綜合分析Pearson 系數值和可視化圖可以發現，與發電量具有較強相關性的為光照強度、電流A 和平均功率，具有中等強度相關性的為板溫，具有較弱相關性的為現場溫度、轉換效率A、轉換效率C、功率C、電流B、電流C、風速和風向，其余特征參數不具有相關性，可忽略不計。

圖5 部分特征參數與發電量的相關性曲線圖

2.3 光伏短期預測結果及分析

通過對不同權重比時的模型預測結果的RMSE作比較，如表2 所示，可以看到，0.8∶0.1 時模型誤差最小。所以賦予特征參數最優權重：光照強度、電流A、平均功率和板溫權重為0.8，其他弱相關性變量權重為0.1，此時，預測值與實際值更為符合。將所有特征參數賦予對應的權重作為預測模型的輸入，得到光伏電站數據集的光伏發電量預測。發現初步預測結果仍有一定誤差，利用前文誤差補償方法，對結果進行誤差補償修正。修正前后的結果對比如圖6 所示。由于式(7)～(9)和歷史實際發電值對初步預測結果的修正作用，使得修正發電量后的預測結果比未經修正的結果誤差降低了37.2%。

表2 不同權重比時的模型RMSE 結果

圖6 誤差修正結果對比

為進一步驗證本文方法的有效性，將本文預測結果與常規LSTM 方法和GA-BP 方法進行比較(圖7)，可以看出，在多峰值處本文方法所得結果更符合原始發電曲線。而通過比較本文方法和LSTM 模型、GA-BP 模型幾個方法的發電量誤差，可以看出，LSTM 模型、GA-BP 模型誤差波動性較強，在－4～2之間波動，誤差較大，而本文方法的誤差穩定在－1～1之間(圖8)，本文方法的誤差相比常規方法至少降低了33.4%。

圖7 光伏預測方法結果對比

圖8 光伏預測方法誤差對比

3 結論

與其它未與GAN 數據增強相結合的常規人工神經網絡方法相比，本文結合太陽數據集對光伏電站小樣本數據集進行數據擴充，通過遷移學習方法優化WGAN 網絡的初始參數設置，在有效擴充新建光伏電站小樣本量的同時保證了生成樣本的質量，提高了生成對抗網絡的泛化能力；充分考慮氣象多元參數作為輸入，并根據相關性大小賦予不同權重，發電預測誤差降低了33.4%。然而，對氣象參數賦予的權重比只適用于光伏場景，其他新能源場景需要根據相關性另作分析；基于GAN 的網絡的訓練階段比較耗時，需要減少訓練階段的計算時間，滿足實時處理的需要。