RESEARCH ANNOUNCEMENTS ON “STRUCTURAL STABILITY OF TRANSONIC SHOCK FLOWS WITH EXTERNAL FORCE”
WENG Shang-kun, YANG Wen-gang
(School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China)
1 Introduction and Main Results
The studies of transonic shock solutions for inviscid compressible flows in different kinds of nozzles had a long history and had obtained many important new achievements during the past twenty years. Courant and Friedrichs[1]had described the transonic shock phenomena in a de Laval nozzle whose cross section decreases first and then increases. It was observed in experiment that if the upcoming flow becomes supersonic after passing through the throat of the nozzle,to match the prescribed appropriately large exit pressure,a shock front intervenes at some place in the diverging part of the nozzle and the gas is compressed and slowed down to subsonic speed.
In this paper,we will consider similar transonic shock phenomena occurring in a flat nozzle when the fluid is exerted with an external force. The 2-D steady compressible isentropic Euler system with external force are of the form where (u1,u2) = u : R2→R2is the unknown velocity filed and ρ : R2→R is the density,and Φ(x1,x2) is a given potential function of external force. For the ideal polytropic gas,the equation of state is given by P(ρ)=ργ, here γ(1 <γ <3) is a positive constant.
To this end, let’s firstly focus on the 1-D steady compressible flow with external force on an interval I =[L0,L1], which is governed by
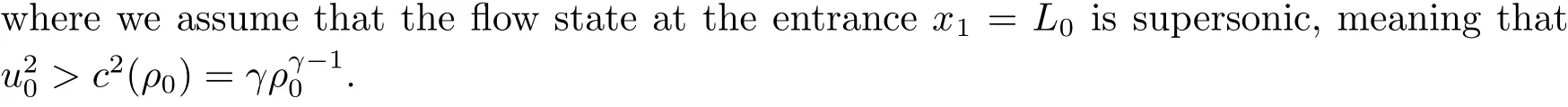
Then it is easy to derive from (1.2) that if the external force satisfies

then the problem(1.2)has a global supersonic solution(ˉρ-,ˉu-)on[L0,L1]. If one prescribes a sufficiently large end pressure at x1= L1, a shock will form at some point x1= Ls∈(L0,L1)and the gas is compressed and slowed down to subsonic speed,the gas pressure will increase to match the given end pressure. Mathematically,one looks for a shock x1=Lsand smooth functions(ˉρ±,ˉu±, ˉP±)defined on I+=[Ls,L1]and I-=[L0,Ls]respectively,which solves (1.2) on I±with the jump at the shock x1= Ls∈(L0,L1) satisfying the physical entropy condition [ˉP(Ls)]= ˉP+(Ls)- ˉP-(Ls)>0 and the Rankine-Hugoniot conditions

and also the boundary conditions
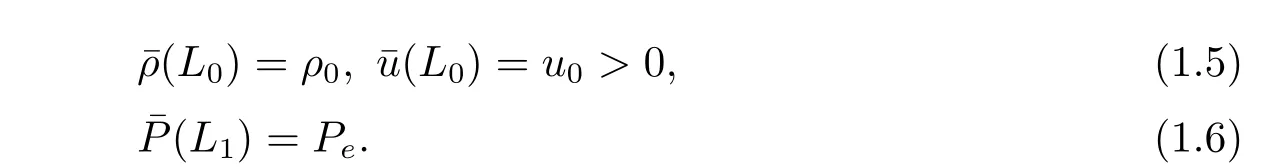
We will show that there is a unique transonic shock solution to the 1-D Euler system when the end pressure Pelies in a suitable interval. Such a problem will be solved by a shooting method employing the monotonicity relation between the shock position and the end pressure.
Lemma 1.1 Suppose that the initial state (u0,ρ0) at x1=L0is supersonic and the external force f satisfying (1.3), there exists two positive constants P0,P1>0 such that if the end pressure Pe∈(P1,P0), there exists a unique transonic shock solution (ˉu-,ˉρ-) and(ˉu+,ˉρ+) defined on I-= [L0,Ls) and I+= (Ls,L1) respectively, with a shock located at x1= Ls∈(L0,L1). In addition, the shock position x1= Lsincreases as the exit pressure Pedecreases. Furthermore, the shock position Lsapproaches to L1if Pegoes to P1and Lstends to L0if Pegoes to P0.
Remark 1 Lemma 1.1 shows that the external force helps to stabilize the transonic shock in flat nozzles and the shock position is uniquely determined.
The one dimensional transonic shock solution(ˉu±,ˉρ±)with a shock occurring at x1=Lsconstructed in Lemma 1.1 will be called the background solution in this paper. The extension of the subsonic flow (ˉu+(x1),ˉρ+(x1)) of the background solution to Ls-δ0<x1<L1for a small positive number δ0will be denoted by (?u+(x1),?ρ+(x1)).
It is natural to further consider the structural stability of this transonic shock flows.For simplicity,we only investigate the structural stability under suitable small perturbations of the end pressure. Therefore, the supersonic incoming flow is unchanged and remains to be (ˉu-(x1),0,ˉρ-(x1)).

Figure 1 Nozzle
Assume that the possible shock curve Σ and the flow behind the shock are denoted by x1= ξ(x2) and (u+1,u+2,P+)(x) respectively (See Figure 1). Let Ω+= {(x1,x2) : ξ(x2) <x1<L1,-1 <x2<1} denotes the subsonic region of the flow. Then the Rankine-Hugoniot conditions on Σ gives

In addition, the pressure P satisfies the physical entropy conditions

Since the flow is tangent to the nozzle walls x2=±1, then

The end pressure is perturbed by
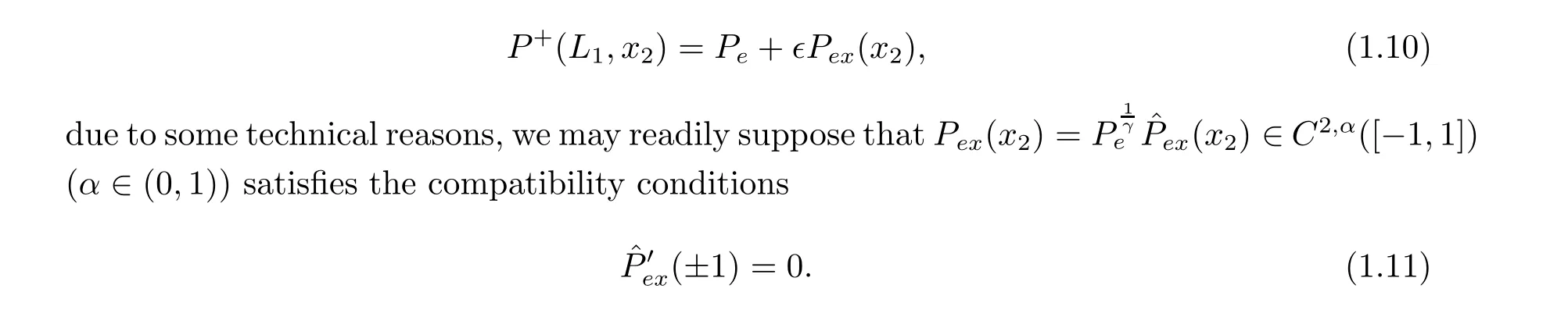
The main results for the structural stability of transonic shock flows with external force can be stated as follows.(i) The shock x1=ξ(x2)∈C3,α([-1,1]), and satisfies
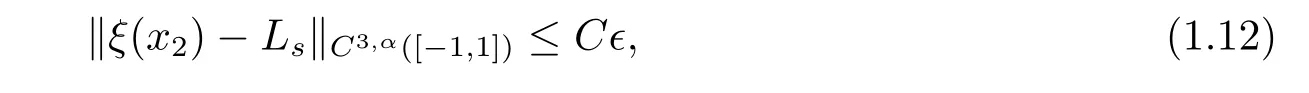

where the positive constant C only depends on the background solution, the exit pressure and α.
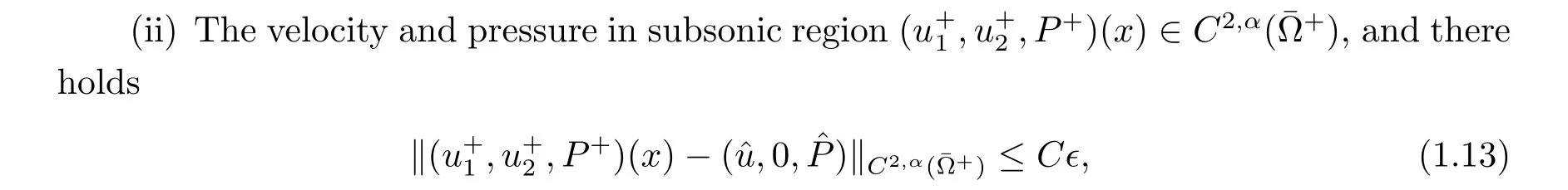
where Ω+={(x1,x2):ξ(x2)<x1<L1,-1 <x2<1} is the subsonic region and(?u,0, ?P)=(?u(x1),0,P(?ρ(x1))) is the extended background solution.
Remark 2 It is well-known that steady Euler equations are hyperbolic-elliptic coupled in subsonic region, several different decomposition of hyperbolic and elliptic modes have been developed in [2, 3, 4]. Here we resort to a different decomposition based on the deformation and curl of the velocity developed in [5] for three dimensional steady Euler systems. The idea in that decomposition is to rewrite the density equation as a Frobenius inner product of a symmetric matrix and the deformation matrix by using the Bernoulli’s law. The vorticity is resolved by an algebraic equation of the Bernoulli’s function.
Remark 3 An interesting issue that deserves a further remark is when using the deformation-curl decomposition to deal with the transonic shock problem, the end pressure boundary condition becomes nonlocal since it involves the information arising from the shock front. However, this nonlocal boundary condition reduces to be local after introducing the potential function.
Remark 4 The structural stability of the transonic shock flow constructed in Lemma 1.1 under small perturbations of supersonic incoming flows and nozzle walls can be proved similarly.
The details of proofs for Lemma 1.1 and Theorem 1.2 can be found in [6].

