海上風電安裝船八邊形樁腿結構輕量化優化分析*

張永康，柯金龍，賴柏豪，高 航，仇 明，顏建軍，鄭和輝，陳旭東，林超輝※

（1.廣東工業大學機電工程學院，廣州 510006；2.大連理工大學，遼寧大連 116086；

3.啟東中遠海運海洋工程有限公司，江蘇啟東 226251；4.招商局重工（江蘇）有限公司，江蘇南通 226100）

0 引言

全球氣候變暖問題持續加重，已成為人類當前面臨的重大挑戰。2020年9月22日，習近平總書記在第七十五屆聯合國大會一般性辯論上宣布，中國將提高國家自主貢獻力度，采取更加有力的政策和措施，力爭2030年前二氧化碳排放達到峰值，努力爭取2060年前實現碳中和[1]。海上風電作為一種新型的清潔能源，日漸受到重視，我國的海上風力發電相關產業發展尤為迅速。2021年，我國海上風電累計裝機量為2 639萬kW，同比增長193.2%，新增裝機量達1 690萬kW，同比增長452.3%[2]。海上風電的迅速發展進一步擴大了大型海上風電安裝船的市場需求。制造出安全高效的海上風電安裝船，是解決海上風電場建設的“卡脖子”難題，是實現國家“雙碳”戰略目標的重要途徑。

樁腿作為自升自航式海上風電安裝船的關鍵支撐結構，在制造過程中需要耗費大量的鋼材。單根八邊形樁腿自重達505 t，樁腿的重量增添了制造、運輸和安裝的難度，并且在遷航過程中需要耗費更多的能源。樁腿結構的輕量化可以助力實現“碳中和”“碳達峰”的節能減排目標。目前，有關樁腿尤其是殼式樁腿的結構輕量化國內外研究文獻較少，國內相關的結構優化文獻為普通船體結構的優化，國外有針對固定平臺的弦杠式樁腿進行結構優化的相關文獻，優化的目標包括輕量化、剛度最大化、疲勞壽命最大化等。可借鑒國內外相關文獻的優化方法，對八邊形殼式樁腿進行結構輕量化處理。

本文將以八邊形樁腿圍板壁厚、導向板壁厚、平臺隔板壁厚、平臺隔板主肋壁厚、圍板肋壁厚為優化目標，以樁腿各構件的許用屈服應力為約束條件，以單根樁腿的重量最輕、屈服等效應力冗余值最小為指標，基于Kriging代理模型和多目標遺傳算法（MOGA）對八邊形樁腿進行結構輕量化處理。

1 Kriging代理模型與遺傳算法

1.1 Kriging代理模型

代理模型是指在分析和優化設計過程中可替代那些比較復雜和費時的數值分析的近似數學模型，也稱為響應面模型、近似模型或元模型[3-4]。代理模型方法不僅可大大提高優化設計效率，而且可降低優化難度，并有利于濾除數值噪聲和實現并行優化設計[5]。

Kriging代理模型一般運用在評估礦產儲備含量及其分布情況。Kriging代理模型在應用時，響應值的樣本點對于鄰近位置的評估與預測性能更佳，但是偏遠樣本點卻對預估發揮的作用偏小。

Kriging模型在使用的時候要求對相關數據做出假設：把欲求解得到的未知函數當做隨機流程的某種展現模式。借助數學方法可以表達成，對于設計變量的任何未知量x，它所呼應的函數值y（x）都能夠借助隨機函數Y（x）進行表達，其中y（x）是Y（x）所有可能結果中的某一個結果，運用公式表述成[6]：

式中：fi(x)為基函數；βi為與之相對應的系數；βifj(x)為Y（x）的數學期望；Z（x）為方差σ2x均值得出為0的靜態隨機計算過程。

若是差異化的設計變量之間，變量與變量之間的協方差能夠表述為[7]：

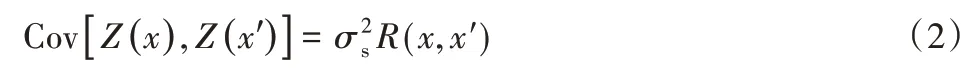
式中：R(x,x′)為同距離相關聯的函數，代表差異化樣本點之間的存在的相關屬性，而且符合在距離是0的時候，R=1，在距離屬于無窮大的時候，R=0，其函數值伴隨著樣本點之間距離的增大而變小。

為使Y（x）可以借助向量體現出來，特此定義兩個特定的k×1的列向量[8]：

聚焦到n個樣本點，可以先定義一個特定的n×k的矩陣[7]：

接著對隨機過程向量進行一定程度的規定[7]：

那么聚焦到n個樣本點所代表的響應值，ys=[ y1,y2,…,yn]T能夠表達成[8]：

樣本點與樣本點之間所體現的矩陣可以規定成R，它由樣本點與樣本點間的一定函數值組成，接著對相關向量rx進行具體定義，rx作全新的樣本點和已知樣本點之間的相關性向量[9]。

因為模型存在無偏估計的要求，也就是E(Z(x))=0，那么在方差是0的時候，則E((x))=fxTβ，所以[8]：

Kriging的誤差能夠展現成[8]：

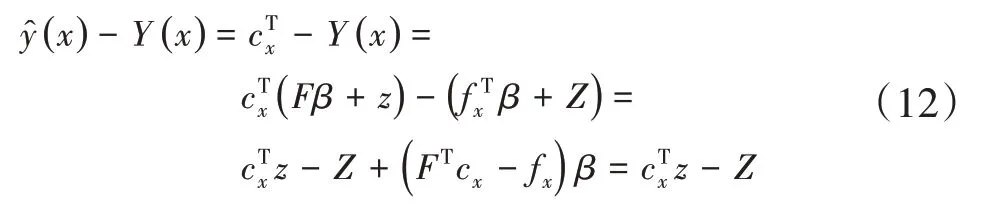
均方差為[7]：

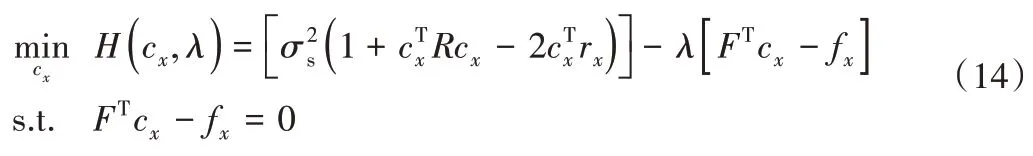
求解后得[7]：

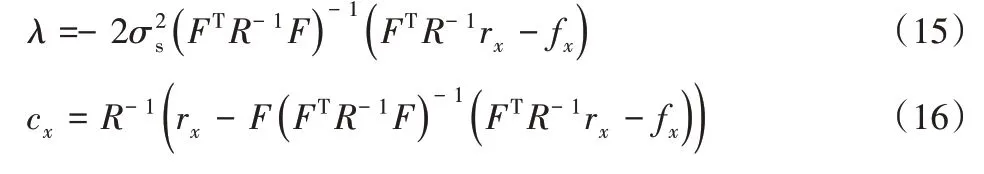
因此得到的預測值為[7]：

其中[8]：

其中，任何位置x*處的值y(x*)服從概率分布，能夠借助N( fTβ,σ2)來表達，那么n個樣本點的觀測值ys=[y(1),y(2),…,y(n)]T，里面的任意觀測點的概率密度為[9]：

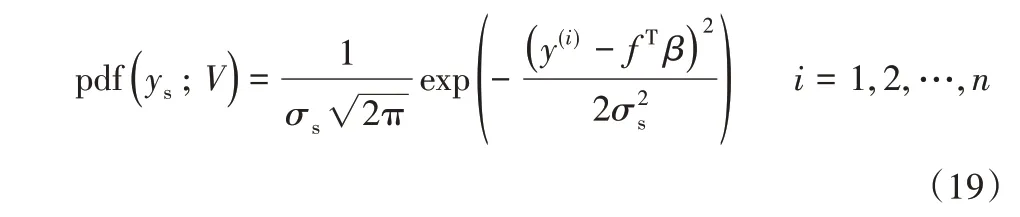
里面的V是待求的未知量β,σ2s，所有樣本集中的聯合密度函數能夠體現為[9]：

取對數得[9]：

對最大似然進行預估，對未知量進行求偏導數，最終得到[9]：

求得[9]：求解得到似然估計值β與σ2s，將兩變量代入對數似然函數，可得[7]：

推出下面的函數，可得相關矩陣R有關的相關參數θ,p[7]：

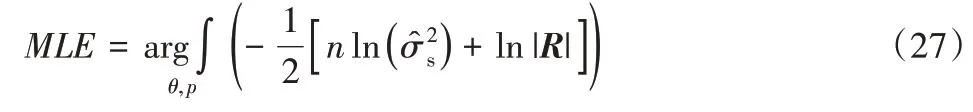
相關向量rx與相關矩陣R表示樣本點間的對應信息，它的值的大小通過相關函數來定義，一定函數值的大小同樣本點與樣本點間的空間距離相關，而且符合下面幾點要求：

（1）在樣本間距離逐步增大時，相關函數的數值會逐漸變小；

（2）在樣本之間的距離大小接近無窮時，相關函數體現出的數值接近0，在兩樣本點數值相同時，也就是樣本間的距離是0，那么相關函數的值是1；

（3）函數必須至少為一階可導；

（4）函數的優化比較簡便。

假定空間中的兩點x(i),x(j)，其相關的模型能夠展現為[8]：

相關函數屬于Kriging模型的關鍵參數，其中的基本原理則是接近的樣本點，二者間的關聯屬性會比較強烈，則值之間的影響更大，若是距離很遠的樣本點，二者間的關聯屬性會偏弱。高斯相關函數是運算中常見的函數，表達公式為[8]：

本文采用高斯函數作為相關函數。

1.2 遺傳算法

遺傳算法（Genetic Algorithm）主要是借鑒生物遺傳進化特征的思想進而演變而成的優化算法，經過Holland[10]指出和不斷發展，遺傳算法衍生出混合遺傳算法[11]、多目標遺傳算法[12]、并行遺傳算法[13]等種類。遺傳算法現階段重點被廣泛使用在工業、數學運算、生物、模擬研究等領域范圍內。

遺傳算法最初應該根據對一些已經進行完善的問題的自變量實施代碼編寫，也就是生物個體的基因代碼的編寫，一般是使用二進制編碼以及實施編碼。個體群眾中處于不斷生長階段劃分成三個方面：選擇、交叉以及突變。遺傳算法的流程見下文所述。

（1）種群初始化

經過編碼準則對需要處理的有效解變換成遺傳環境下的染色體，每一個個體的代碼表示為自變量的數值，一般的編碼準則包含了二進制編碼、實數代碼編碼、多級參數編碼等，本文采取實數代碼準則。

（2）適應度函數

適應度函數的作用是進行劃分個體的優和差，為選擇提供了基本參照，通常能夠通過目標函數改變來獲取，基于優化的條件來開展，假如應該搜索優化問題的最低值，那么優化值越低，也就表示適應度越高，優化函數的倒數能夠表示為適應函數；假如應該搜索優化問題的最高值，那么被完善之后的函數就能夠表示成為適應函數。通過搜索優化問題的最高值作為參照，適應度計算函數表示成[14]：

（3）選擇操作

選擇操作采用選出勝者、淘汰劣質的方式開展不斷完善，適應度比較好的個體有更大的概率生殖繁衍后代，個體能夠被選擇出來的概率和個體本身的適應度存在聯系，個體適應度表現得越好，那么將會有很大可能被選擇成為交叉對象，然而適應度最優的個體并不是100%能夠被指定的，若選擇流程上采取輪盤賭法，那么第i個體能夠被選擇的概率是[14]：

式中：Fi為第i個出現個體的適應度值；N為群體里面的個體數量。

（4）交叉操作

交叉操作也就是在上一代中產生出新個體，這種新個體帶有在上一代個體中的比較優秀的遺傳基因，而運作的流程為上一代中個體里面選取兩個個體，經過兩個染色體的互換與合并，將上一代里面優異的代表性基因保留給后代，組成適應程度更優的個體。因為編碼形式為實數編碼，則ak和a1處于j開展交叉的步驟如下[64]：

式中：η為[0,1]中的隨機數。

（5）變異操作

變異是一種自然現象，想要維持物種的多樣性，基因處于進化期間將會出現突變，某種突變可能造成個體的適應度減弱，然而某種突變也會表現出個體的適應度得到提升，造成優化溢出局部最優解之外。變異操作通過在全部群體里面任意挑選出某個體，之后通過在被指定的個體里面的某基因點位置進行突變。比如第i個體的j個基因aij變異步驟如下[14]：

式中：amax為基因aij的上界；amin為基因aij的下界；r2與r為一個隨機數；g為現階段迭代數；Gmax為最大迭代數（提早選擇）。

遺傳算法基于群體中個體的不斷優化獲取的最優數值，而不是對單個個體進行優化，因此優化后的解更能代表整個種群，而非種群中的某個局部。因為適應度函數的運算和優化函數存在著根本聯系，不通過運算取得其余的信息值，方便產生貫通的流程。

2 Kriging+MOGA優化模型參數

單一目標優化法使用一個優化指標來評價優化效果，多目標優化法使用兩個或以上的優化指標來評估優化效果的優劣，這些優化指標之間相互排斥影響，多目標遺傳算法（MOGA）與單一目標遺傳算法相比，優化過程更為復雜，但更符合實際，在實際工程中得到了更為廣泛的運用。然而多目標遺傳算法（MOGA）由于要計算較多的目標函數，在優化過程中收斂慢、耗時長，需要付出較大的時間成本和經濟成本，針對這一缺陷，本文引入Kriging代理模型，與MOGA多目標遺傳算法結合，大大降低了運算量及迭代次數，縮短了優化的時間，提升了優化的效率。

本文對風電安裝船的樁腿進行多目標優化設計，目標為：樁腿質量最輕，用鋼量最少；樁腿應力冗余值最小，最大程度發揮鋼材的強度，減少結構冗余。

對于樁腿結構各部分進行參數化定義，本次優化針對板材厚度，自變量以及設計值如表1所示。按照原設計值，樁腿重量為504 644 kg。

表1 自變量參數

樁腿質量M與自變量呈正比例關系，可表達為：

因此，樁腿的輕量化優化可用如下方程式表示：

式中：V-min為向量極小化，即向量f()x中的各子目標函數都盡可能地極小；s.t.為多目標優化過程中的約束條件，約束條件包括樁腿等效應力小于許用應力，對于樁腿各結構應力分布條件的限制，參考表2對樁腿各部件材料許用應力的計算。

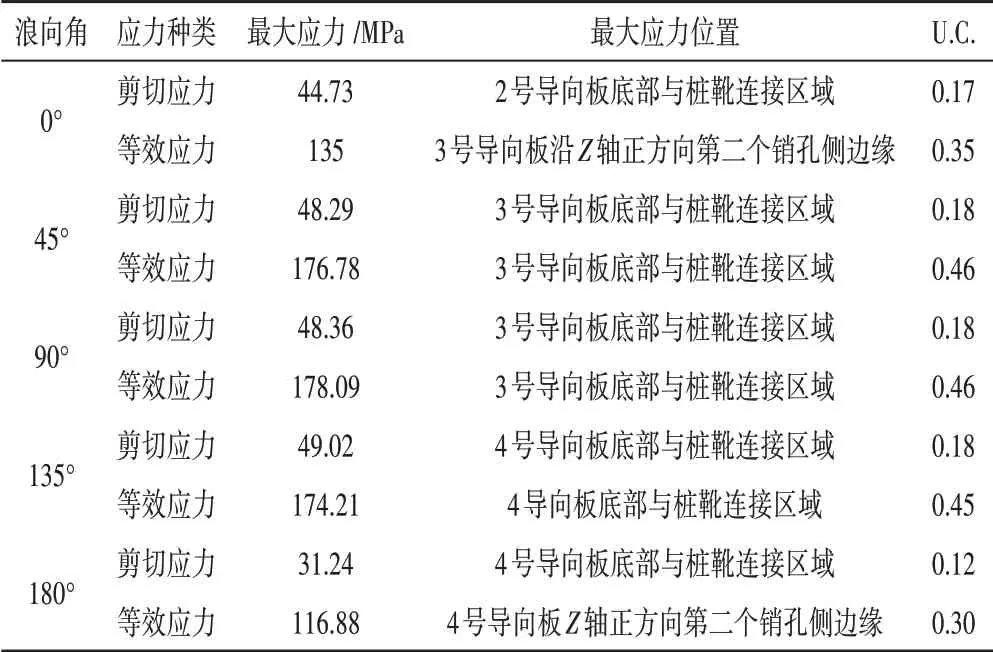
表2 樁腿導向板強度校核結果

為節省計算時間，提高最優解搜索效率，自變量x1,x2,x3,x4,x5的取值范圍約束在初始設計值的0.5～1.1倍。

本文采用ANSYS Workbench對八邊形樁腿結構進行參數化建模，以風暴自存工況，90°浪向角為設計優化工況，通過Design Explorer模塊進行結構輕量化優化，引入Kriging代理模型和MOGA優化算法，初始樣本數為100，每次迭代樣本數為80，收斂穩定率為2%，最大迭代次數為30次，最大候選樣本數為3個。具體優化計算流程如圖1所示。

圖1 優化計算流程

3 優化結果分析

本文在ANSYS Workbench中建立參數化有限元模型，采用原設計值，對有限元模型進行靜力計算。經過10次迭代后，全部自變量參數計算收斂，由于計算采用Kriging代理模型，大部分樣本結果由Kriging模型預測給出，實際進行有限元計算的樣本數為361個。

圖2所示為圍板壁厚的迭代優化過程。圍板初始設計值為0.02 m，在1～3次迭代中樣本點均布于優化約束條件限定的范圍內，最小樣本點下探至0.01 m，在3次迭代后樣本點均位于0.012 m以上并逐漸向下收斂，在第8次迭代完成后基本收斂穩定，圍板的優化值收斂于0.012 m附近，壁厚減少幅度達40%，優化結果與設計初始值有較大差距。由此可見圍板對于樁腿的整體力學強度貢獻率較小，在保證安全的前提下可以進行較大幅度的減重。

圖2 圍板壁厚優化迭代過程

圖3所示為導向板壁厚的優化迭代過程。導向板的初始設計值為0.1 m；在第1～2次迭代過程中，樣本點均勻散布于設計值的0.6～1.1倍之間；在第2次迭代過程中，樣本點出現向上收斂趨勢；在第3～5次迭代過程中，樣本點位于0.085～0.11 m之間。第7次迭代導向板壁厚穩定收斂于0.096 m附近，壁厚減少幅度為4%。導向板壁厚優化幅度相對于圍板壁厚來說較小，這是由于導向板是八邊形樁腿的關鍵結構部件，有較高的綜合力學性能要求。

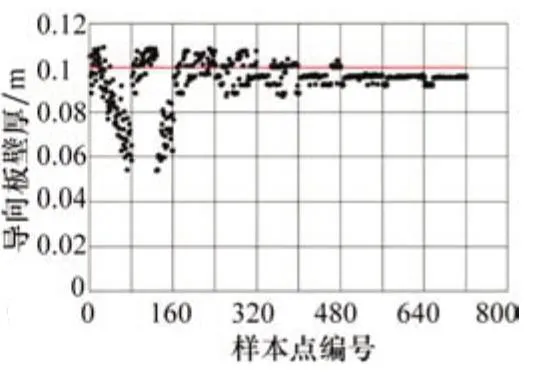
圖3 導向板壁厚優化迭代過程

圖4所示為平臺隔板壁厚的優化迭代過程。平臺隔板的初始設計值為0.015 m。在9次迭代過程中，樣本點均勻分布在為提高計算設定的約束范圍之內，并沒有明顯的收斂趨勢。因此，平臺隔板壁厚對樁腿整體優化的影響較小，優化值可取在設計值附近。

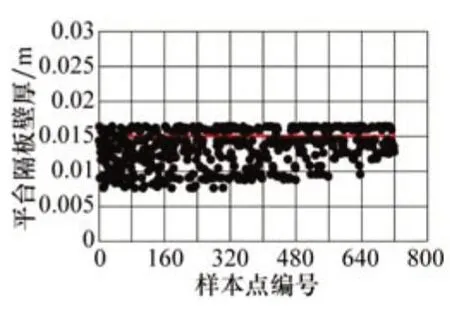
圖4 平臺隔板壁厚優化迭代過程

圖5所示為平臺隔板主肋壁厚的優化迭代過程。平臺隔板主肋的初始設計值為0.012 m；在1～4次迭代過程中，有樣本點的值超過初始的設計值；在第5次迭代后，樣本點有朝下集中的趨勢；從第6次迭代開始，有約80%的樣本點集中在0.006 5～0.008 m；但在10次迭代后平臺隔板肋壁厚的樣本始終沒有體現出收斂的特性，數值分布于0.006～0.012 m左右。由于在本次優化中，平臺隔板主肋重量較小，壁厚變化對八邊形樁腿整體質量影響不大，優化結果呈一定的發散性。平臺隔板肋對平臺整體的力學性能起到加強的作用，在對樁腿整體重量影響不大的前提下，應優先選用較厚的壁厚，使用平臺隔板肋壁厚的初始設計值即可。

圖5 平臺隔板主肋壁厚優化迭代過程

圖6所示為圍板肋壁厚的迭代優化過程。圍板肋壁厚設計初始值為0.025；迭代過程較慢，在第4次迭代過程中出現收斂趨勢，最后在第7次迭代后穩定收斂于0.013 m附近；優化后的壁厚減少幅度為48%，可優化的幅度較大。圍板肋是圍板的加強結構，圍板的壁厚減少幅度達40%，可見圍板和圍板肋結構存在較大的應力儲備冗余和優化空間。

圖6 圍板肋壁厚優化迭代過程

圖7樁腿質量優化迭代過程

圖7所示為八邊形樁腿質量在10次迭代過程中的變化，可以發現樁腿質量呈現較為明顯的收斂趨勢。1～3次迭代，樁腿質量呈現較為明顯的離散型，在第3次迭代后收斂速度加快并開始呈現收斂趨勢，在第6次迭代后穩定收斂于41 000 kg附近。

圖8所示為樁腿最大應力的迭代優化過程，趨勢與圖7樁腿質量的迭代優化相似，1～2次迭代優化效果較差，樣本點沿設置的約束條件區間均布，第3次迭代后，樣本點開始呈現出收斂趨勢，并逐漸加快收斂速度，在9～10次迭代過程中，樣本點穩定收斂于280 MPa附近。由于樁腿最大應力發生于材料為NVE-690的導向板部位，而樁腿的大部分結構為NVE-420，因此限制了最大應力接近約束條件中NV690的最大許用應力336 MPa。

圖8 樁腿最大應力優化迭代過程

根據計算結果，在各樣本點中選出3個較優候選樣本點，與初始設計值對比如表3所示。由表可知，3個候選點樁腿質量相近，候選點1質量最小，相比原樁腿質量降低19.3%。考慮實際工程應用，為方便加工及圖紙管理，各構件的尺寸應取為整數，故取平臺隔板肋骨厚度為0.008 m，圍板肋厚度為0.013 m，圍板厚度為0.013 m，導向板厚度為0.093 m，平臺隔板厚度為0.015 m。

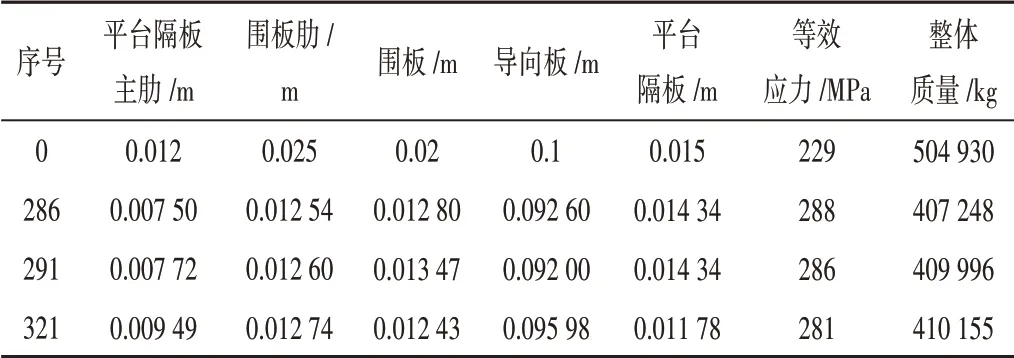
表3 候選點與初始設計值對比

按上述優化的尺寸在ANSYS中重新建立單個八邊形樁腿的模型。浪向角為90°的風暴自存工況是八邊形樁腿的最危險工況[15]，因此在Workbench中對該工況下樁腿位移和等效應力進行了分析。

樁腿等效應力云圖如圖9所示。樁腿的最大等效應力出現于導向板的第一個銷孔附近，為287.7 MPa，考慮了動力因素后導向板的許用應力為387.10 MPa，等效應力的U.C值為0.74；參照表2，導向板在浪向角為90°的風暴自存工況下等效應力的U.C值為0.46。優化前后的等效應力儲備程度降低，利用率提升了61%，極大地降低了強度冗余。

圖9 候選點1應力云圖

位移分布如圖10所示，八邊形樁腿的最大位移出現在樁腿頂部，位移為305 mm，而通過計算腿頂部Y方向位移可知在浪向角為90°的風暴自存工況下樁腿最大位移為128 mm，最大位移有較大增加，輕量化后的樁腿將會削弱了樁腿的剛度。

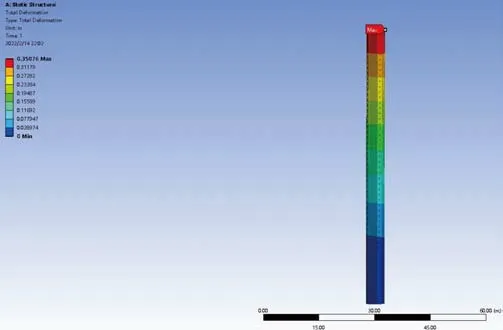
圖10 候選點1的位移圖

本優化計算表明，樁腿結構設計較為保守，存在較大的優化空間，使用多目標優化的方法有利于降低樁腿質量和應力冗余程度，減少用鋼量，提高結構的強度利用率。

4 結束語

本文基于Kriging代理模型和多目標遺傳算法（MOGA），以八邊形樁腿的圍板壁厚、導向板壁厚、平臺隔板壁厚、平臺隔板主肋壁厚、圍板肋壁厚為優化目標，根據相關規范設置合理的約束條件，對樁腿結構進行了優化分析，得到以下結論：

（1）八邊形樁腿的強度滿足設計要求，在橫浪時樁腿結構等效應力最大U.C值小于0.75，應力裕度充足且導向板、平臺隔板等結構應力存在一定的冗余度。

（2）優化結果顯示，取平臺隔板肋骨厚度為0.007 5 m、圍板肋厚度為0.013 m、圍板厚度為0.013 m、導向板厚度為0.093 m、平臺隔板厚度為0.015 m，樁腿質量相比原設計方案降低19.3%，且最大應力和最大位移均在許用范圍內，初步達到了輕量化、降低應力冗余的目標。