LabVIEW一階系統(tǒng)虛擬教學(xué)實(shí)驗(yàn)系統(tǒng)開發(fā)

鹿 堯

（南京理工大學(xué)機(jī)械工程學(xué)院，南京 210094）

0 引言

隨著虛擬儀技術(shù)的發(fā)展，基于虛擬儀器的虛擬教學(xué)系統(tǒng)的開發(fā)也隨之得到社會(huì)的關(guān)注。虛擬儀器是通過一些軟件平臺(tái)可以把電腦與一些程序模塊整合，操作者可以通過這些軟件平臺(tái)和程序模塊自主定義、設(shè)計(jì)虛擬實(shí)驗(yàn)[1]。虛擬儀器之所以會(huì)發(fā)展如此迅速，與傳統(tǒng)儀器提供了強(qiáng)大的理論支持和操作基礎(chǔ)密不可分。表1所示為兩者之間的比較。

表1 兩種儀器的對(duì)比

下面舉出幾個(gè)國(guó)外的虛擬儀器的例子：如美國(guó)國(guó)防部高級(jí)研究與發(fā)展計(jì)劃聯(lián)合開發(fā)了虛擬仿真互聯(lián)網(wǎng)平臺(tái)系統(tǒng)VINT[2]；由美國(guó)俄勒岡大學(xué)物理系主辦的物理實(shí)驗(yàn)網(wǎng)站VLAB[3]；美國(guó)巴爾的摩一個(gè)基于Java技術(shù)的虛擬物理實(shí)驗(yàn)室項(xiàng)目[4]；德國(guó)魯爾大學(xué)開發(fā)的VClab實(shí)驗(yàn)室[5]；由新加坡國(guó)立大學(xué)電子工程系開發(fā)的工程教育虛擬實(shí)驗(yàn)室[6]。

盡管中國(guó)對(duì)虛擬儀器的研究起步較晚，但是這些年里也是有所發(fā)展。如中國(guó)科技大學(xué)研制出了幾何光學(xué)設(shè)計(jì)平臺(tái)的物理虛擬實(shí)驗(yàn)室[7]；北京大學(xué)計(jì)算機(jī)系設(shè)計(jì)開發(fā)的流水線實(shí)驗(yàn)和CACHE實(shí)驗(yàn)兩套網(wǎng)絡(luò)虛擬實(shí)驗(yàn)室[8]；華中科技大學(xué)開發(fā)了液壓回路性能和液壓元件裝拆虛擬實(shí)驗(yàn)[9]；北京師范大學(xué)現(xiàn)代教育技術(shù)研究研制了一個(gè)基于虛擬空間的三維電子線路實(shí)驗(yàn)環(huán)境的Evlab系統(tǒng)[10]。此外，虛擬儀器如口腔實(shí)驗(yàn)教學(xué)[11]、細(xì)胞遺傳學(xué)實(shí)驗(yàn)[12]等醫(yī)學(xué)應(yīng)用方面也有很大的進(jìn)步；并且在管理學(xué)方面也有所發(fā)展，如區(qū)塊鏈+電子商務(wù)虛擬實(shí)驗(yàn)[13]等方面的研究。

本文基于虛擬儀器軟件——LabVIEW對(duì)一階慣性系統(tǒng)進(jìn)行網(wǎng)上虛擬實(shí)驗(yàn)的搭建。一方面完成了一套一階慣性系統(tǒng)的仿真和PID控制實(shí)驗(yàn)，有助于緩解現(xiàn)實(shí)中的實(shí)驗(yàn)教學(xué)資源分布不均衡，可以降低實(shí)驗(yàn)室所屬的相關(guān)單位的財(cái)務(wù)開銷，使得使用者對(duì)一階慣性系統(tǒng)和PID控制了解更加簡(jiǎn)單，方便和易懂；另一方面針對(duì)一階慣性系統(tǒng)的PID控制，利用本次搭建的實(shí)驗(yàn)系統(tǒng)中經(jīng)過PID控制后得到的系統(tǒng)時(shí)域響應(yīng)圖，通過更改PID控制中的變量參數(shù)，對(duì)比不同變量產(chǎn)生的時(shí)域響應(yīng)圖最終可以得出PID控制中積分單元、微分單元和增益單元對(duì)系統(tǒng)的影響[14-15]。

1 一階系統(tǒng)虛擬教學(xué)實(shí)驗(yàn)的基礎(chǔ)理論

1.1 一階系統(tǒng)概述

則可以得出其幅頻特性為：

對(duì)于一階慣性系統(tǒng)的波德圖的計(jì)算，以式（2）為例，其對(duì)數(shù)幅頻特性為，對(duì)數(shù)相頻特性為φ(w)=-arctanwT。

在LabVIEW上模擬出當(dāng)凈增益K=1，時(shí)間常數(shù)時(shí)的結(jié)果如圖1所示。

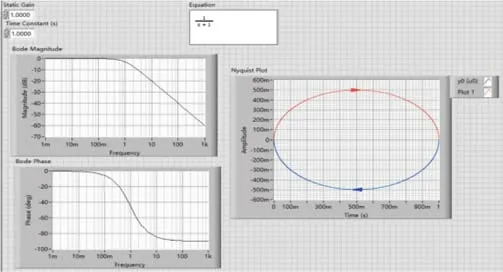
圖1 典型一階慣性系統(tǒng)頻率特性

1.2 一階系統(tǒng)的單位階躍響應(yīng)

當(dāng)階躍信號(hào)作為系統(tǒng)的輸入信號(hào)時(shí)，首先階躍信號(hào)其數(shù)學(xué)表達(dá)式可以表示為經(jīng)過拉普拉斯變換之后的拉氏變換式為R(s)=，則上述系統(tǒng)的該時(shí)間響應(yīng)的拉氏變換式為：

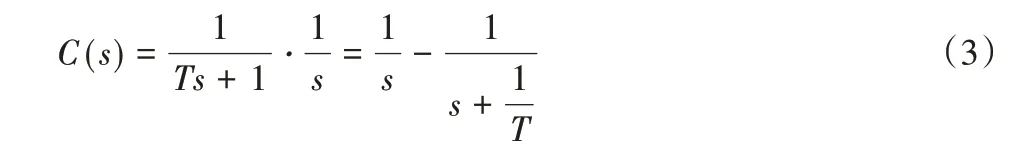
再將式（3）經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為：

用LabVIEW模擬出來的一階慣性系統(tǒng)的單位階躍響應(yīng)前面板如圖2所示。

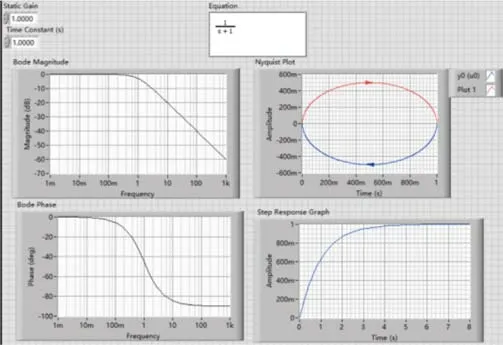
圖2 一階系統(tǒng)單位階躍響應(yīng)

簡(jiǎn)單介紹該曲線的相關(guān)特性。由式（3）可以計(jì)算出時(shí)間響應(yīng)曲線的初始斜率：

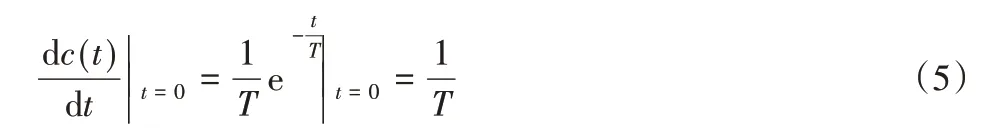
式（5）有利于計(jì)算出該一階慣性系統(tǒng)的時(shí)間常數(shù)，對(duì)于圖2中的一階慣性系統(tǒng)的時(shí)間常數(shù)即為1。

該一階慣性系統(tǒng)階躍響應(yīng)曲線最終趨于一定值的曲線，并且該系統(tǒng)并不具備振蕩特征。因此該系統(tǒng)的時(shí)間響應(yīng)并沒有超調(diào)量。

最后，也可以直接從圖2看出，當(dāng)t→+∞時(shí)，系統(tǒng)的穩(wěn)態(tài)誤差

1.3 一階系統(tǒng)的單位脈沖響應(yīng)

當(dāng)脈沖信號(hào)作為系統(tǒng)的輸入信號(hào)時(shí)，首先脈沖信號(hào)其數(shù)學(xué)表達(dá)式可以表示為，經(jīng)過拉普拉斯變換之后的拉氏變換式為R(s)=1，則上述系統(tǒng)的該時(shí)間響應(yīng)的拉氏變換式為：

再將式（6）經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為：

用LabVIEW模擬出來的一階慣性系統(tǒng)的單位脈沖響應(yīng)前面板如圖3所示。

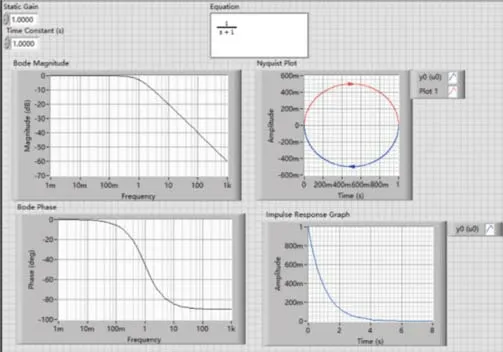
圖3 一階系統(tǒng)單位脈沖響應(yīng)

對(duì)于一階系統(tǒng)的單位脈沖響應(yīng)信號(hào)曲線，當(dāng)時(shí)間t逐漸增加，直至當(dāng)t→+∞時(shí)，c(t)=0。因此一階系統(tǒng)的單位脈沖響應(yīng)無穩(wěn)態(tài)分量。計(jì)算該時(shí)間響應(yīng)曲線的初始斜率

2 虛擬教學(xué)實(shí)驗(yàn)設(shè)計(jì)

LabVIEW中有兩種PID控制器的控件，一種是測(cè)量測(cè)試使用的PID控件，另一種就是此次設(shè)計(jì)所需要的控制設(shè)計(jì)與仿真模塊的PID控件。

PID控制也叫比例積分微分控制，它兼具比例微分控制的改善系統(tǒng)動(dòng)態(tài)品質(zhì)和比例積分控制的：

式中：Kp為比例單元增益系數(shù)；Ti為積分單元的系數(shù)；Td為微分單元的系數(shù)。

在PID控制中各個(gè)單元的作用也有不同，具體如下。

（1）比例單元通俗地說就是一個(gè)起到放大作用的單元，比例單元的系數(shù)越大，放大的倍數(shù)也就越大，但是被控制、被調(diào)節(jié)的參數(shù)的曲線波動(dòng)也越大。系統(tǒng)在比例單元運(yùn)作時(shí)也會(huì)因?yàn)楸壤龁卧糯蟮臅r(shí)候會(huì)產(chǎn)生與實(shí)際被測(cè)參數(shù)產(chǎn)生偏差，這時(shí)候就需要引入積分單元進(jìn)行工作。

（2）積分單元的作用就是當(dāng)系統(tǒng)產(chǎn)生偏差時(shí)，積分單元就會(huì)隨著時(shí)間進(jìn)行積累，逐漸抵消這個(gè)偏差，只要偏差一直存在，積分單元將會(huì)一直運(yùn)行。

（3）微分單元的作用就是解決被控對(duì)象的滯后問題。

一階系統(tǒng)PID控制實(shí)驗(yàn)設(shè)計(jì)如下。

對(duì)一階系統(tǒng)先進(jìn)行PID控制再進(jìn)行時(shí)間響應(yīng)。前面內(nèi)容已經(jīng)介紹了一階系統(tǒng)的傳遞函數(shù)而PID控制的傳遞函數(shù)將兩個(gè)傳遞函數(shù)相乘得出整個(gè)系統(tǒng)的傳遞函數(shù)為：

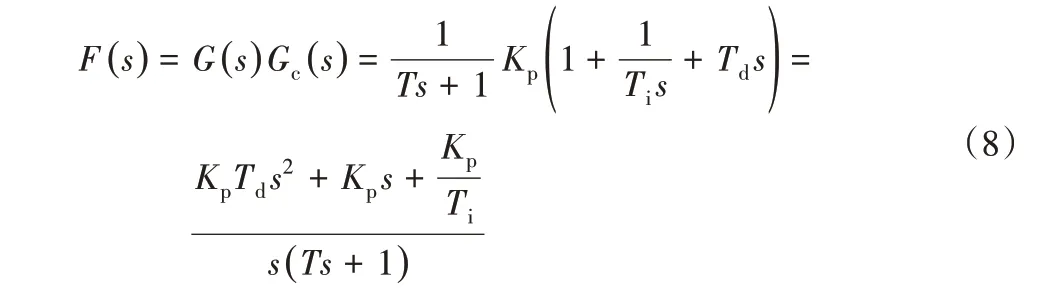
下面通過幾個(gè)示例進(jìn)行對(duì)比，來觀察整個(gè)系統(tǒng)的時(shí)間響應(yīng)有什么區(qū)別。

對(duì)于同一個(gè)一階系統(tǒng)，假設(shè)其時(shí)間常數(shù)為1，凈增益也為1，那么這個(gè)一階系統(tǒng)的傳遞函數(shù)就為G(s)=。對(duì)于這樣一個(gè)一階系統(tǒng)，每次只改變PID控制中3個(gè)參數(shù)其中一個(gè)，再給予這整個(gè)系統(tǒng)一個(gè)相同的時(shí)間響應(yīng)，觀察最終的響應(yīng)信號(hào)的時(shí)域圖。

2.1 整個(gè)系統(tǒng)的單位階躍響應(yīng)

先取PID控制環(huán)節(jié)的3個(gè)參數(shù)：比例系數(shù)為20，積分系數(shù)為0，微分系數(shù)為0.01，得出PID控制環(huán)節(jié)傳遞函數(shù)為Gc(s)=0.2s+20，那么整個(gè)系統(tǒng)的傳遞函數(shù)即為F(s)=。當(dāng)整個(gè)系統(tǒng)的時(shí)間響應(yīng)為單位階躍響應(yīng)，其拉普拉斯變換式為R(s)=1s時(shí)，則上述系統(tǒng)的該時(shí)間響應(yīng)的拉氏變換式為C(s)=再將C（s）經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為：

用LabVIEW對(duì)上面的計(jì)算環(huán)節(jié)進(jìn)行模擬，如圖4所示。

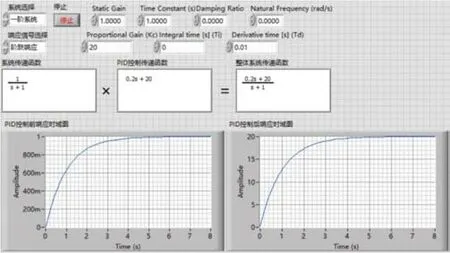
圖4 整體系統(tǒng)的單位階躍響應(yīng)時(shí)域圖

當(dāng)只改變PID控制環(huán)節(jié)中的一個(gè)參數(shù)，保持另外兩個(gè)參數(shù)不變?cè)龠M(jìn)行處理。先改變比例系數(shù)，不改變微分系數(shù)和積分系數(shù)，使比例系數(shù)由20變?yōu)?0。于是PID控制環(huán)節(jié)的傳遞函數(shù)就變?yōu)镚c(s)=0.4s+40，整體系統(tǒng)的傳遞函數(shù)為F(s)=當(dāng)相同的單位階躍響應(yīng)作用在這個(gè)系統(tǒng)上時(shí)可以得出輸出的拉氏變換式為，再對(duì)C（s）經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為

用LabVIEW對(duì)上面的計(jì)算環(huán)節(jié)進(jìn)行模擬，如圖5所示。

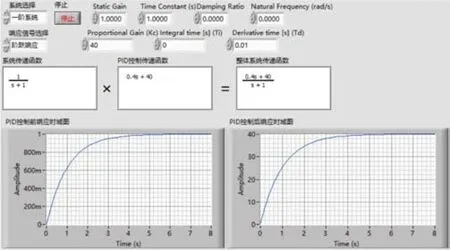
圖5 Kp=40時(shí)整體系統(tǒng)的單位階躍響應(yīng)時(shí)域圖

再保持原來的比例系數(shù)20不變，只改變積分系數(shù)，不改變微分系數(shù)，把積分系數(shù)由原來的0改為0.1。于是PID控制環(huán)節(jié)的傳遞函數(shù)就變?yōu)椋w系統(tǒng)的傳遞函數(shù)為，當(dāng)相同的單位階躍響應(yīng)作用在這個(gè)系統(tǒng)上時(shí)可以得出輸出的拉氏變換式為C(s)=，再對(duì)C（s）經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為：

用LabVIEW對(duì)上面的計(jì)算環(huán)節(jié)進(jìn)行模擬，如圖6所示，發(fā)現(xiàn)該時(shí)域圖發(fā)散。

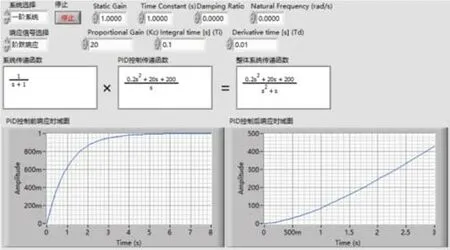
圖6 Ti=0.1時(shí)整體系統(tǒng)的單位階躍響應(yīng)時(shí)域圖

再保持原來的比例系數(shù)和積分系數(shù)不變，只改變微分系數(shù)，使微分系數(shù)由0.01變?yōu)?.2。于是PID控制環(huán)節(jié)的傳遞函數(shù)就變?yōu)镚c(s)=4s+20，整體系統(tǒng)的傳遞函數(shù)為F(s)=，當(dāng)相同的單位階躍響應(yīng)作用在這個(gè)系統(tǒng)上時(shí)可以得出輸出的拉氏變換式為再對(duì)C（s）經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為：

用LabVIEW對(duì)上面的計(jì)算環(huán)節(jié)進(jìn)行模擬，如圖7所示。

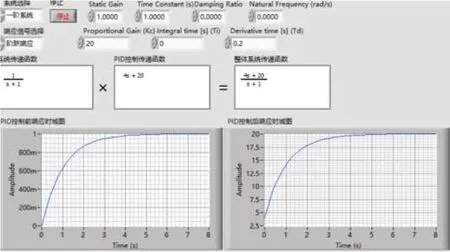
圖7 Td=0.2時(shí)整體系統(tǒng)的單位階躍響應(yīng)時(shí)域圖

2.2 整個(gè)系統(tǒng)的單位脈沖響應(yīng)

對(duì)于相同的PID控制環(huán)節(jié)，其傳遞函數(shù)為Gc(s)=那么整個(gè)系統(tǒng)的傳遞函數(shù)即為F(s)=當(dāng)整個(gè)系統(tǒng)的時(shí)間響應(yīng)為單位脈沖響應(yīng)，其拉普拉斯變換式為R()s=1時(shí)，可以得出整個(gè)系統(tǒng)的輸出的拉氏變換式為再對(duì)C（s）經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為：

用LabVIEW對(duì)上面的計(jì)算環(huán)節(jié)進(jìn)行模擬，如圖8所示。

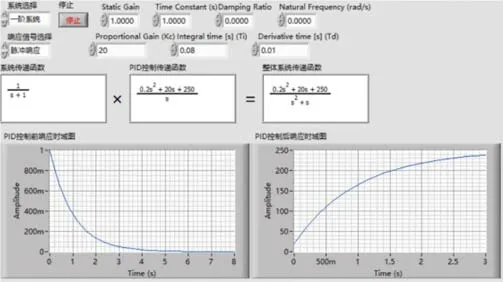
圖8 整體系統(tǒng)的單位脈沖響應(yīng)時(shí)域圖

當(dāng)只改變PID控制環(huán)節(jié)中的一個(gè)參數(shù)，保持另外兩個(gè)參數(shù)不變?cè)龠M(jìn)行處理。先改變比例系數(shù)，不改變微分系數(shù)和積分系數(shù)，使比例系數(shù)由20變?yōu)?0。于是PID控制環(huán)節(jié)的傳遞函數(shù)就變?yōu)檎w系統(tǒng)的傳遞函數(shù)為，當(dāng)相同的單位脈沖響應(yīng)作用在這個(gè)系統(tǒng)上時(shí)可以得出輸出的拉氏變換式為C(s)=，再對(duì)C(s)經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為：

用LabVIEW對(duì)上面的計(jì)算環(huán)節(jié)進(jìn)行模擬，如圖9所示。

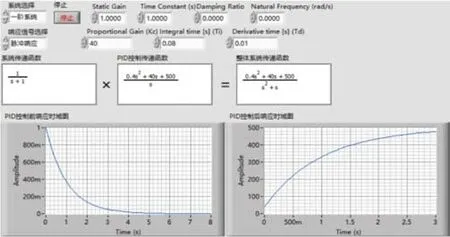
圖9 Kp=40時(shí)整體系統(tǒng)的單位脈沖響應(yīng)時(shí)域圖

再保持原來的比例系數(shù)20不變，只改變積分系數(shù)，不改變微分系數(shù)，把積分系數(shù)由原來的0.08改為0.16。于是PID控制環(huán)節(jié)的傳遞函數(shù)就變?yōu)檎w系統(tǒng)的傳遞函數(shù)為，當(dāng)相同的單位脈沖響應(yīng)作用在這個(gè)系統(tǒng)上時(shí)可以得出輸出的拉氏變換式為C(s)=，再對(duì)C(s)經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為：

用LabVIEW對(duì)上面的計(jì)算環(huán)節(jié)進(jìn)行模擬，如圖10所示。

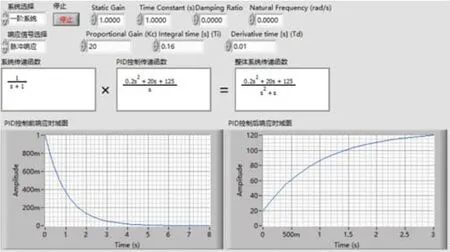
圖10 Ti=0.16時(shí)整體系統(tǒng)的單位脈沖響應(yīng)時(shí)域圖

再保持原來的比例系數(shù)和積分系數(shù)不變，只改變微分系數(shù)，使微分系數(shù)由0.01變?yōu)?.2。于是PID控制環(huán)節(jié)的傳遞函數(shù)就變?yōu)椋w系統(tǒng)的傳遞函數(shù)為，當(dāng)相同的單位脈沖響應(yīng)作用在這個(gè)系統(tǒng)上時(shí)可以得出輸出的拉氏變換式為再對(duì)C(s)經(jīng)過拉普拉斯反變換轉(zhuǎn)化成數(shù)學(xué)表達(dá)式。得到輸出的原函數(shù)為：

用LabVIEW對(duì)上面的計(jì)算環(huán)節(jié)進(jìn)行模擬，如圖11所示。

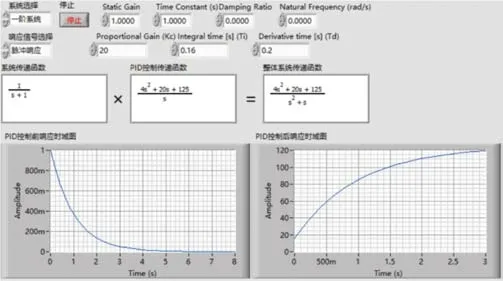
圖11 Td=0.2時(shí)整體系統(tǒng)的單位脈沖響應(yīng)時(shí)域圖

3 結(jié)束語

本文利用LabVIEW設(shè)計(jì)了一款一階慣性系統(tǒng)的相關(guān)特性和PID控制下一階慣性系統(tǒng)的時(shí)域圖，可以完成對(duì)于一階慣性系統(tǒng)的部分控制實(shí)驗(yàn)，完全開發(fā)達(dá)到使用者直接通過對(duì)實(shí)驗(yàn)系統(tǒng)前面版相關(guān)系數(shù)的更改來獲得所希望的一階慣性系統(tǒng)和PID控制效果的要求。

同時(shí)根據(jù)仿真數(shù)據(jù)可以直接得出對(duì)于相同的時(shí)間響應(yīng)信號(hào)，PID控制環(huán)節(jié)的參數(shù)的改變對(duì)于其輸出的時(shí)域圖的影響可以總結(jié)得出：（1）當(dāng)積分系數(shù)和微分系數(shù)相同時(shí)，比例系數(shù)越大，時(shí)間響應(yīng)曲線在穩(wěn)定前的增加速率越大；（2）當(dāng)比例系數(shù)和微分系數(shù)相同時(shí)，積分環(huán)節(jié)系數(shù)越大，時(shí)間響應(yīng)曲線在穩(wěn)定前的增長(zhǎng)速率減小；（3）當(dāng)比例系數(shù)和積分系數(shù)相同時(shí)，微分系數(shù)對(duì)于整個(gè)系統(tǒng)的影響較小。