非結構網格熱化學非平衡Navier-Stokes方程組求解技術研究

朱海濤，李巖，蘭子奇

中國航空研究院數字仿真中心，北京 100012

準確預測高超聲速飛行器周圍的氣動熱力學環境是設計、發展和評估新型高超聲速飛行器的關鍵[1]。由于飛行速度很大，在黏性和強激波壓縮作用下，氣體巨大的動能轉化為內能，致使高超聲速飛行器所處的氣動熱力學環境異常苛刻。在地面復現這種高溫高焓環境非常困難，進而很難通過風洞試驗較為準確地預測高超聲速飛行的氣動熱力學參數，而且成本高昂。高溫氣體物理化學特性的深入研究和高性能計算技術的快速發展使得先進的計算流體力學方法成為預測高超聲速飛行器氣動熱力學特性不可或缺的重要手段[2]。

數值模擬技術很早便被應用于高超聲速流場氣動熱力學計算。早在20世紀80年代，C.Park等[3]對高溫高焓空氣的化學反應速率、熱力學參數、輸運性質等物理、化學特性進行了研究和總結，建立了考慮真實氣體效應的三維熱化學非平衡Navier-Stokes 方程組。此后，高超聲速繞流場數值模擬技術得以快速發展；其中具有代表性的是:M. P.Netterfield 等[4]通過求解二溫度熱化學非平衡Navier-Stokes 方程組獲得了球模型的熱化學非平衡數值流場，從中提取了激波位置、駐點溫度和組分分布等信息，該算例成為計算高超聲速熱化學非平衡數值流場的常用對比算例；J.Muylaert 等[5]研究了完全催化邊界條件和完全非催化邊界條件對高超聲速飛行器氣動熱計算結果的影響，并與風洞試驗和飛行試驗結果進行對比分析，該算例成為氣動熱計算的典型對比算例。除此之外，高超聲速流動數值模擬的廣度不斷擴大，開始探索氣動熱力學環境多物理場耦合數值模擬。例如，B.Hassan等[6]在氣/固界面處構造質量、能量平衡的耦合交互面，完成了IRV-2 頭部球錐段熱化學非平衡流動、非定常材料熱響應和燒蝕過程的耦合計算研究，給出了多個彈道點上的表面熱流和溫度分布。隨著火星著落器、星際探測器的興起，飛行器的速度進一步提高，高溫氣體內各種非線性物理機制對高超聲速飛行器氣動熱力學環境的影響已無法忽略。描述這些復雜物理機制的新的數學模型也不斷被應用于高超聲速流場數值計算。例如，Marschall等[7]總結了歐盟航空航天領域使用的多種有限速率催化和化學反應模型，并提出了有限速率表面化學反應的一般框架，用于描述氣/固界面熱量、能量輸運過程。

熱化學非平衡Navier-Stokes 方程組數值求解技術也是國內的研究熱點。董維中等[8]采用多個振動溫度氣體模型完成了半球模型和球錐模型繞流的數值模擬，細致研究了氣體模型對激波脫落距離、壁面熱流、溫度分布的影響；高鐵鎖等[9]通過數值求解熱化學非平衡Navier-Stokes方程組獲得高溫空氣組分和溫度分布，然后基于輻射傳輸方程，利用高溫氣體組分的主要輻射機制，計算分析了輻射加熱對返回艙熱環境的影響；張子健等[10]提出了一種理論分析和數值模擬相結合的兩步漸進法，研究了振動激發過程對二維斜劈氣動力/氣動熱特性的影響規律。董維中等[11]開發了三維熱化學非平衡Navier-Stokes 方程組求解軟件AEROPH Flow，可以考慮熱力學非平衡效應、表面催化效應、燒蝕等因素的影響。鄒學峰等[12]對高超聲速飛行器熱/力/振動/噪聲多學科耦合技術的研究進展進行了綜述。

高超聲速技術的蓬勃發展，促使新型熱防護技術、主動流動控制技術以及新型控制舵面等新技術快速應用于工程實踐。因此，高超聲速飛行器的幾何外形越來越復雜，結構形式越來越多樣化，基于結構網格的數值模擬技術已不能很好地滿足工程實際需求。為此，美國國家航空航天局（NASA）啟動了Fundamental Aeronautics Program 項目[13]，發展非結構網格計算技術和基于非結構網格的網格自適應技術即為其中的重要研究內容，并用于發展高可靠性、高效的高超聲速熱化學非平衡流動數值模擬工具。這個研究領域也引起國內研究者的重視。李鵬等[14]在我國自主開源CFD 軟件“風雷”中也開發了非結構網格計算功能，但沒有看到詳細的計算結果。

本文采用非結構混合網格技術求解三維熱化學非平衡Navier-Stokes方程組，與結構網格計算結果進行對比分析，驗證了數值求解工具的有效性；同時，針對邊界層網格分布和小組分氣體計算問題進行了計算研究，并給出了實施建議。

1 熱化學非平衡Navier-Stokes方程組

熱化學非平衡Navier-Stokes 方程組由經典Navier-Stokes 方程組和描述物理、化學非平衡效應及其耦合效應的模型方程組構成。本文數值計算程序可以計及振動能激發態和離解及置換化學反應，尚無法考慮電子能激發態、光輻射和電離反應。因此，熱力學非平衡效應采用二溫度模型；化學非平衡效應采用有限速度化學反應模型；二者的耦合效應僅考慮振動溫度與離解化學反應之間的相互影響。本文數值求解的熱化學非平衡Navier-Stokes方程組為

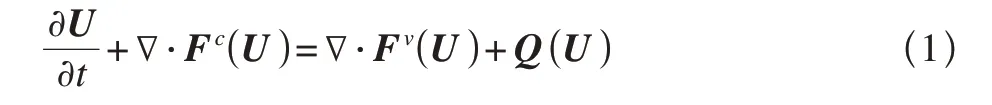
式中

其中，前ns個方程為各個組分的質量守恒方程，其后為三個方向的動量守恒方程，然后是能量守恒方程，最后是振動能方程。U為包含ns個組分的守恒變量:ρi為組分i的密度，ρu,ρE,ρev分別為單位體積混合氣體總動量矢量、總能量和總振動能，ρ為混合氣體總密度，u,E,ev分別為混合氣體質量平均速度矢量和單位質量的總能量、振動能。Fc為對流通量項，I為單位矩陣，p為混合氣體壓強。Fv為黏性通量項，Ji是組分i的質量擴散通量，遵循Fick擴散定律；τ是黏性應力張量；q是熱傳導通量，遵循Fourier 熱傳導定律，由平動—轉動溫度和振動溫度兩部分構成；qv是僅由振動溫度確定的熱傳導通量項。Q是源項:ωi是化學反應過程中組分i的生成速率，ωvt是平動—轉動態和振動態能量轉換過程中振動能生成項，可由Landau-Teller 理論建立不同能量態轉換松弛方程是單位質量組分i的振動能量，ωi是由化學反應導致組分i質量變化，進而引起的振動能改變量。這些方程組是不封閉的，需補充以下數理方程。

1.1 熱力學方程

熱力學方程包括氣體狀態方程和各能量態內能計算公式。本文采用二溫度模型，即平動—轉動溫度Ttr和振動溫度Tv，混合氣體的總能量

式中，ei是組分i平動和轉動能的和。對分子組分

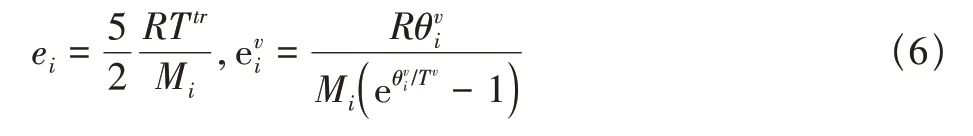
原子組分沒有轉動和振動能，因此

各組分的分壓力僅與平動溫度有關，進而混合氣體的狀態方程為

式中，R為普適氣體常數；Mi、分別為組分i的摩爾質量和振動特征溫度。

平動—轉動模式與振動模式之間存在能量交換。由Landao-Teller理論可知振動能的時間變化率為

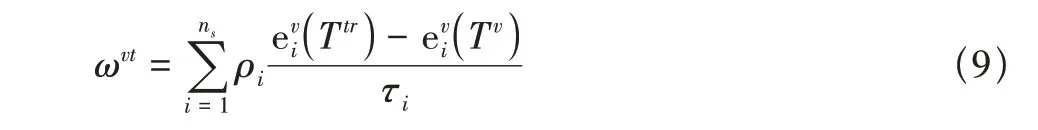
1.2 化學反應模型

對于有nr個化學反應的模型，組分i的生成率為

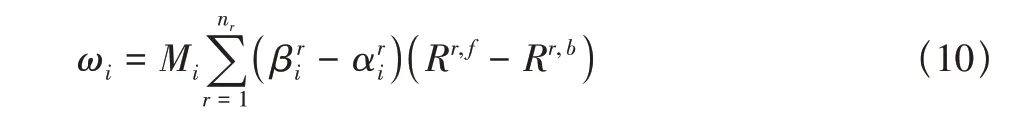
Gupta 給出了高溫空氣化學反應平衡系數Kr,eq的經驗擬合公式，進而可得逆反應的化學反應速率系數為

本文采用5 組分、17 個化學反應的空氣化學模型，式（10）、式（11）中用到的常數和經驗擬合公式可見參考文獻[1]。

1.3 熱力學—化學反應非平衡耦合模型

利用化學反應控制溫度T建立化學反應非平衡與熱力學非平衡之間的耦合關系。5組分空氣模型包含置換和離解兩類化學反應。采用Park 優先離解模型，置換化學反應的控制溫度與平動—轉動溫度一致，即T=Ttr；離解反應的控制溫度由平動—轉動溫度和振動溫度確定，計算公式為T=。

1.4 輸運系數

方程組（1）中需要的輸運系數有:氣體黏度μi、平動—轉動導熱系數、振動導熱系數λvi和質量擴散系數Di。單個組分的黏度和導熱系數用Blotter高溫氣體黏度擬合公式和Eucken經驗關系式計算；混合氣體黏度和導熱系數通過Wilke半經驗公式，根據各個組分進行加權平均。擴散系數采用雙組元模型計算。具體計算公式可參見參考文獻[1]。

式（1）、式（5）、式（8）～式（10）和輸運系數計算公式構成封閉的熱化學非平衡Navier-Stokes 方程組。引入適當邊界條件后構成適定的偏微分方程組初邊值問題，即可進行數值求解。本文采用的邊界條件包括超聲速入口和出口邊界條件、對稱邊界條件、等溫壁面邊界條件、完全非催化和完全催化邊界條件。

2 數值求解方法

對方程組（1）進行空間積分，并采用格點有限元方法離散，在單元控制體上可得如下半離散方程組

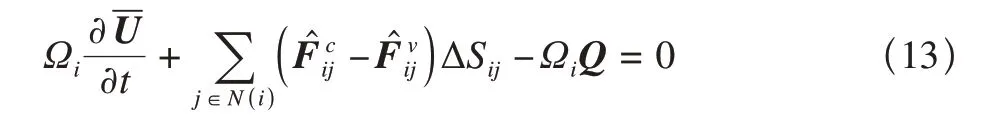
式中，Ωi為網格點i對應的控制體積；N(i)是與點i相鄰的網格點集；j是與點i相鄰的點，ΔSij是網格邊ij對應的對偶網格面積。對流通量項采用AUSM格式計算；黏性通量項首先在各個控制體內采用最小二乘法計算每個網格點上的空間導數值，然后對相鄰兩點進行平均獲得對偶網格面上流動變量、輸運系數和相關空間導數值，再計算黏性通量項；源項采用分片常數近似直接在控制內積分。

非平衡效應和各個源項使得離散后線性方程組矩陣條件數很大，數值剛性問題嚴重。因此在時間離散時，對流通量項和源項進行隱式處理

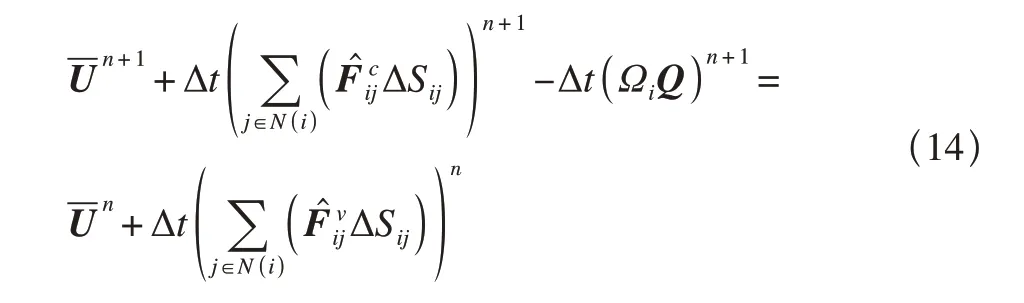
完成空間、時間離散后，采用GMRES算法求解所得線性方程組以更新下一時間步流場信息。

2.1 非結構網格布置

相對于傳統亞、跨、超聲速流場，高超聲速流場具有多組分、高熱焓、強激波、強熱化學非平衡的特征。基于前者流場特征的非結構混合網格布置規則，能否適用于后者，需進行專門研究。本文以公認結構網格計算結果為基準，對非結構混合網格y+、邊界層網格規模、增長率等因素進行細致研究，為高超聲速非結構混合網格技術的工程應用奠定基礎。

2.2 小組分氣體計算

由于高超聲速流場熱化學非平衡效應，式（13）、式（14）具有很強的數值剛性。不斷積累的數值殘差對小組分氣體計算產生嚴重不利影響。本文在計算化學反應生成項時，引入元素摩爾數守恒關系式，對一部分組分氣體采用式（10）直接計算，其余組分氣體由元素摩爾數守恒關系式計算。對5組分空氣模型而言，根據元素摩爾數守恒，有

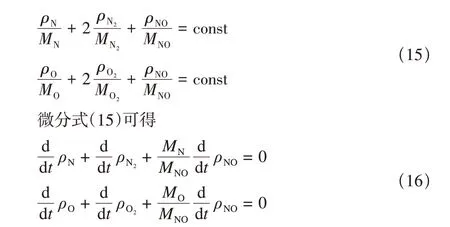
計算過程中，對分子組分N2，O2，NO 采用式（10）直接計算，而原子組分采用式（16）計算，保證各元素摩爾數守恒。與公認的結構網格計算結果對比表明，這種計算方法顯著改善了小組分氣體的計算準確度。

3 數值結果與分析

本文采用基于非結構混合網格的三維熱化學非平衡Navier-Stokes 方程組求解程序計算了半球模型、RAMC II模型高超聲速繞流場，并與公認的、采用結構網格的計算結果進行對比分析，還討論了非結構混合網格邊界層網格點布置和小組分氣體準確計算問題。

3.1 半球模型

半球模型的半徑r= 6.35mm；自由來流速度V∞=5280m/s，靜溫T∞= 293K，靜壓p∞= 664Pa；基于球半徑的雷諾數Re=14600。壁面采用完全非催化等溫邊界條件，壁溫Tw= 2000K。實際計算中僅取1/4 球面，并采用對稱邊界條件。

采用4套非結構混合網格，著重考察邊界層網格y+、網格增長率γ對數值結果的影響。邊界層內棱柱層數目L、邊網層網格點數nb和整體計算域網格點數ng等網格參數見表1；其中y+值是駐點附近區域的數值。

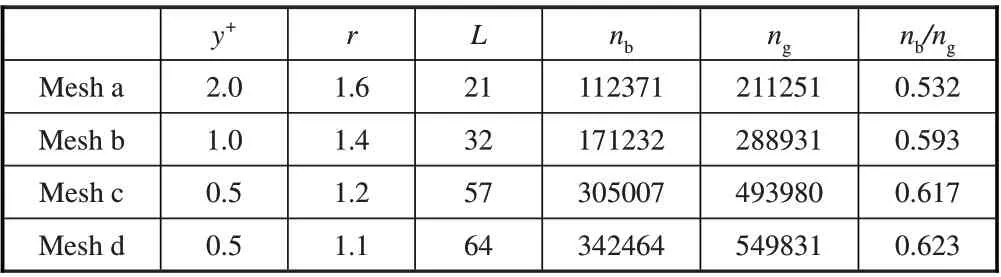
表1 4套非結構混合網格參數Table 1 Main parameters of four unstructured mesh used in present computation

圖1給出了物面熱流計算結果與公認結構網格計算數據[8]的對比圖。由于本文采用全三維計算，圖中熱流值是每隔15°抽取一條經線，共計13 條經線上熱流的平均值。橫坐標是經線弧長與球半徑的比值。可以看出，第四套網格所得物面熱流與公認解基本吻合。由于公認解采用二維軸對稱熱化學非平衡Navier-Stokes 方程組，無法計及繞緯線方向的流動的影響，因此二者在駐點下游區域存在相對較大的差異。

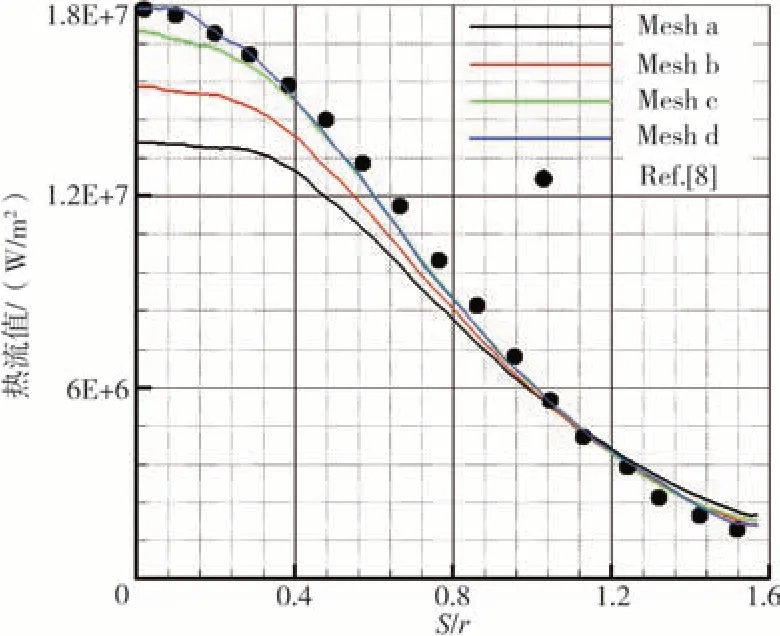
圖1 物面熱流(w/m2)曲線與公認解[8]對比圖Fig.1 Sphere model heat flux(w/m2)of present comparison with reference[8]

圖2給出了駐點線上平動—轉動溫度和振動溫度分布與公認結構網格計算數據的對比圖。在圖2（a）中，第三、第四套網格計算結果與公認結果吻合較好，激波位置也吻合良好。在圖2（b）中，非結構網格計算結果與結構網格有較明顯的差異:本文最高振動溫度出現在激波位置稍下游，與激波比較接近，而結構網格所得最高振動溫度與激波有較遠的距離。造成差異的原因可能有:（1）振動能控制方程與化學反應、內能模式轉化緊密相關，本文采用5組分空氣模型，而參考文獻[8]采用了7組分或11組分化學模型；（2）本文是全三維計算，而參考文獻[8]采用二維軸對稱計算，造成流場分布存在差異。

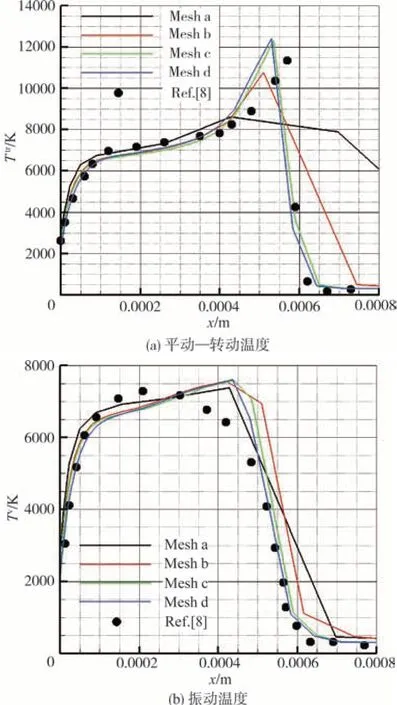
圖2 駐點線上平動—轉動溫度和振動溫度分布曲線與公認解[8]對比圖Fig.2 Translational-rotational temperature and vibrational temperature in stagnation line of present computation comparison with reference[8]

以參考文獻[8]為參考解，可以看出熱流對網格分布的要求比流場變量更為苛刻；為了獲得準確的熱流分布結果，邊界層網格y+值應不超過1，邊界層增長率應介于1.1～1.2，盡可能使邊界層網格點數不低于總網格點數的60%。

3.2 RAMC II模型

RAMC Ⅱ是一個球錐模型，頭部球半徑為0.1524m，球錐半頂角為9°，軸向長度為1.295m。計算工況為:飛行高度61km；自由來流靜壓19.2Pa，靜溫244.3K；飛行馬赫數23.9，基于球半徑雷諾數19866。物面采用完全非催化等溫邊界條件，壁溫Tw= 1500K。參考文獻[15]給出了采用結構網格的詳細計算結果。通過與該公認解的對比分析，討論采用非結構混合網格計算時，兩種化學反應源項計算方法對小組分氣體數值結果的影響:第一種方法是直接采用式（10）計算各個組分的化學反應生成項；第二種方法是由式（10）和元素摩爾守恒關系式（16）計算各個組分化學反應生成項。

圖3給出了駐點線上各組分質量分數分布曲線與公認解的對比結果。其中圖3（a）、圖3（b）分別給出了直接計算法（方法一）和采用組分摩爾數守恒關系計算法（方法二）所得結果與公認解的對比結果；圖3（c）是兩種計算方法結果的對比圖。可以看出，兩種計算方法所得組分質量分數結果與公認解均有一定差異。參考文獻[15]采用7 組分空氣模型進行二維軸對稱計算，因此與本文結果有較明顯差異。相對于公認解，采用第二種方法差異更小。由圖3（c）可見，兩種計算方法對NO組分的影響最為顯著。原因是在邊界層內混合氣體的溫度已超過8000K，氧分子已完全離解為氧原子；此時，相對于氮氣、氮原子和氧原子，NO組分為小組分氣體，對積累的數值誤差最為敏感。因此，為保證對小組分氣體的準確計算，應采用元素摩爾數守恒關系式計算方法。

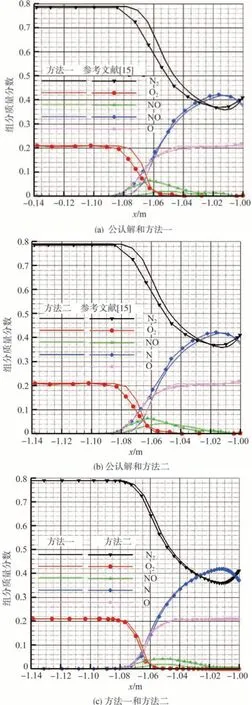
圖3 駐點線上各組分質量分數分布曲線與公認解[15]對比圖Fig.3 Mass fraction in stagnation line of present computation comparison with reference[15]

4 結論

采用非結構混合網格技術求解三維熱化學非平衡Navier-Stokes 方程組，通過與典型算例公認結構網格數值結果進行對比驗證，檢驗了本文數值方法的正確性和有效性。應用本文計算程序，討論了在采用非結構混合網格進行高超聲速流場數值模擬時，邊界層網格布置和小組分氣體準確計算問題，得到如下結論:

（1）盡管非結構混合網格具有顯著的不規則性，且控制方程組離散后系統數值剛性很大，但采用該技術也可以獲得與結構網格較一致的流場和熱流計算結果。

（2）邊界層網格布置對物面熱流計算結果影響顯著；對二階格式而言，為保證對物面熱流的正確計算，邊界層網格y+應小于1（0.5左右），網格增長率應不超過1.4（1.1～1.2）。

（3）小組分氣體對數值誤差積累較為敏感，為準確計算小組分氣體，在化學反應源項計算過程中，應采用元素摩爾數守恒關系式。