基于MEMS的航空壓力傳感器結構力學分析

何毓銘，徐雅潔，朱江，李述林

1.航空工業南京機電液壓工程研究中心，江蘇 南京 211100

2.中國空軍試飛局，陜西 西安 710000

力學在航空領域已取得巨大成就，隨著科技的發展，人們研究的對象逐漸向微納米尺度發展。在航空領域中出現越來越多的微尺度結構器件，如常見的微機電系統，其內部結構一般在微米甚至納米量級，是一個獨立的智能系統，具有體積小、耗能低、重量（質量）輕、響應時間短等優點。

美國空軍早在20 世紀末就開展了微機電系統傳感器在飛機上應用的可行性研究，進行了大量的地面和空中試驗。2004年，北大西洋公約組織就針對微機電系統技術在航空領域應用中開展了一系列的研究。隨著現代微機電系統的飛速發展[1-3]，近年來微機電陀螺儀研制工作進展很快，目前美國已經開始批量生產由硅微陀螺和硅加速度計構成的微型慣性測量裝置。其低成本、低能耗及體積小、重量輕的特點很適于戰術應用，在航空領域最先應用于導彈和無人機。

美國洛克希德-馬丁公司在20世紀末就著手研究微機電系統在軍用飛機上應用的可行性。同時應用于現役的F-16戰斗機。據悉，微機電系統傳感器內嵌于戰斗機的輪胎，可以對輪胎的膨脹壓力和溫度進行感應和傳輸，并跟蹤輪胎系列號，幫助監控輪胎狀態從而延長其使用壽命，如美國海軍的H46直升機在輪胎內部嵌入微機電傳感器，使維修停飛期縮短了一半，減少故障30%，每年節約維修費用約6000 萬美元。

微尺度梁作為傳感器乃至微機電系統中最為重要的核心部件之一，對其力學性能的分析具有非常重要的應用價值，但是傳統的經典彈性理論并不適用于微小尺度。這個結論來源于幾個早期的試驗，N.Fleck[4]等對退火后的不同尺寸銅絲做了拉伸和扭轉試驗，Nix和Gao研究了單晶銀薄膜的硬度與壓痕深度的關系。試驗均表明，當尺寸為微尺度時，材料的參數就會發生顯著變化，這種現象我們稱它為尺度效應。最早對微觀尺度力學性能做出解釋的是Voigt，他于1887年提出了偶應力理論，他認為材料內部存在力偶作用。Cosserat 在偶應力理論基礎上發展了很多高階連續理論。20 世紀60 年代，由R.A.Toupin[5]、R.Mindlin[6]等逐漸完善了偶應力理論，應變能只考慮轉動向量的梯度，因此只需要兩個材料特征尺寸參數，才讓這個理論在學術界有了一個科學的影響力。之后。Fleck 和Hutchinson 等提出了一種應變梯度理論，它考慮了轉動應變梯度影響作用，之后F.Yang[7]在這個理論基礎上提出了修正偶應力理論，這個理論有三個材料特征尺寸參數。Duhem 于1893 年提出了非局部理論，作為最早提出非局部理論的人，他認為一點的應力應該和整個區域內所有點的應變都有關系。直到1971年A.Eringen[8-10]和Edelen 等才系統建立非局部理論，這個理論闡述了一個連續體的某個參照點的應力和整個區域內每個點的應變都有關系，此理論也成功解釋了之前經典力學理論無法解決的微觀尺度問題。最開始的非局部理論是積分形式，后來Eringen[8-10]考慮了一個特定核函數將其化為微分形式，微分形式由于形式簡單，至此以后被廣泛應用到微納米結構中的力學分析[11-15]中。

在研究這些微尺度結構時，傳統經典彈性理論已經不再適用。此時我們必須考慮材料的內部特征[16-18]。在研究尺度效應[19-22]中，Eringen非局部模型在微觀領域中得到了廣泛的應用，它是一種應變驅動本構方程，即某點的應力與整個區域的應變分布有關，結果體現了尺度效應中的弱化效應，然而在有些情況下卻存在不一致的結果，如懸臂梁受集中力作用沒有體現出尺度效應。本文則是基于應力驅動的非局部積分模型，即某點的應變與整個區域的應力分布有關，對微尺度結構中的微梁進行結構力學分析，從而研究尺度效應[23-25]。

1 應力驅動的非局部理論積分模型

在微觀結構中，當傳統彈性理論變得不足時，非局部效應會更加明顯，這有助于研究非局部理論。Eringen 非局部線性彈性理論是文獻中使用最廣泛的方法之一。參考點的非局部應力不僅取決于該點的應變，還取決于該區域中所有其他點的應變。在非局部理論中，經典彈性理論被替換。該理論的本構關系解釋了原子與內部長度尺度之間的作用力，并已應用于許多問題，包括波傳播、斷裂力學等。Eringen非局部理論積分模型是應變驅動本構方程，本文則是基于應力驅動本構方程，即某點的應變和整個區域的應力分布有關。

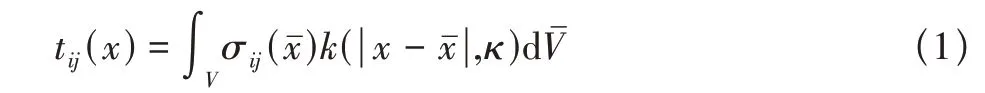
式中，tij(x)是應變；σij(xˉ)是應力；κ是一個關于內部長度尺度的非局部參數。

如果引入局部效應的影響，此時該模型可以轉換為如下形式

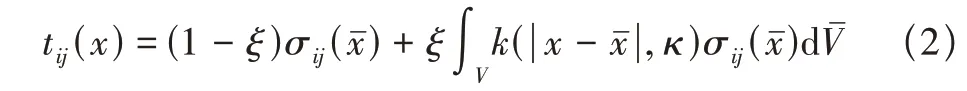
式中，ζ可以看作兩相局部參數材料的一個參數，在此研究中，還可以將內核函數表述為以下形式

于是我們可以得到兩相非局部參數積分模型的最終表達式

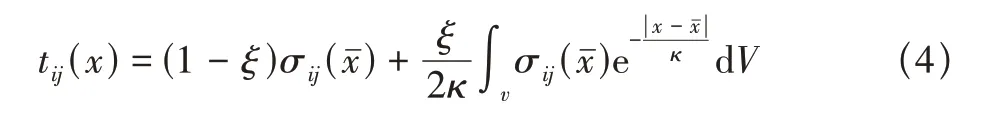
2 歐拉梁

對于歐拉梁，將基于應力驅動本構關系利用兩相非局部理論積分模型，通過化簡將Fredholm 型積分方程化為Volterra 型積分方程，并使用拉普拉斯變換求解微分方程。此處將采用解析求解并代入數值得到最后的數值解。根據不同邊界情況，具體求解出不同邊界情況下不同結果數據。在此先對一個通式進行拉普拉斯變換得到一個相關的結論，之后的內容將直接使用這個結論。

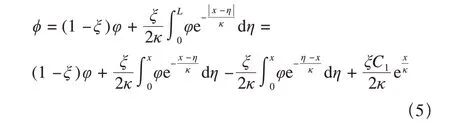
其中

再對上述等式兩端進行拉普拉斯變換，可以化簡為

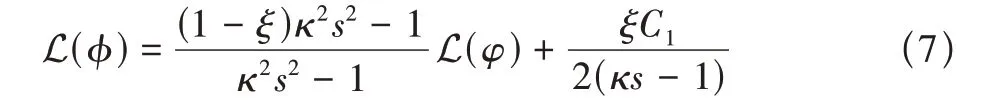
所以對滿足方程（5）的等式兩端均進行拉普拉斯變換，可以得到方程（7）這種結果。

2.1 歐拉梁的靜態彎曲

如圖1 所示建立模型，梁的長度為L，寬度為b，高度為h。由于此類問題和寬度b無關，因此可以將寬度設為1。

圖1 歐拉梁模型Fig.1 Euler-bernoulli beam model

假定位移場為

式中，w(x,t)為橫向位移。

應變能為

假定歐拉梁受到橫向的均勻分布載荷，大小為q，則外力功為

根據哈密頓變分原理同理可得控制方程為

和邊界條件為

其中

應力驅動本構方程為

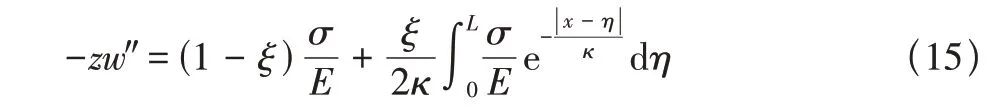
根據方程（14），可化為

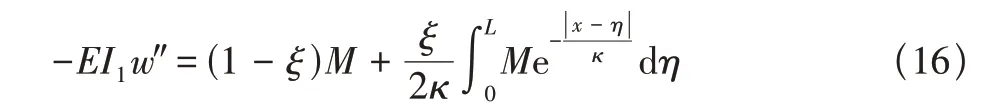
其中

對方程（11）等號兩邊都進行拉普拉斯變換，得到

將方程（16）等號兩邊進行拉普拉斯變換，得到

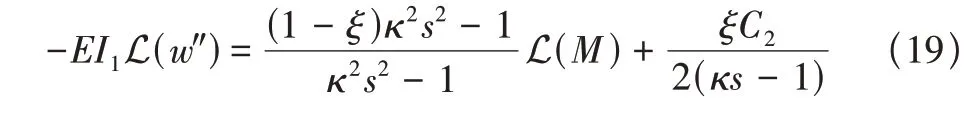
其中

將方程（18）和方程（19）聯立為一個方程組，可以求解出L(M)和L(ω)，再進行拉普拉斯逆變換便得到M和ω的解析解。其中解析式中未知常量可以根據式（12）、式（13）、式（20）和拉普拉斯變換的微分性質求出。

以兩端固支，受到橫向均勻分布載荷的邊界條件為例，邊界條件為

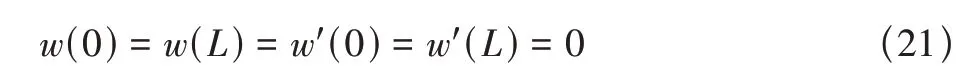
只觀察撓度最大的點即x=L/2處的撓度，得到的無量綱化（本文無量綱化均為除以經典彈性理論下的數值）的撓度表達式

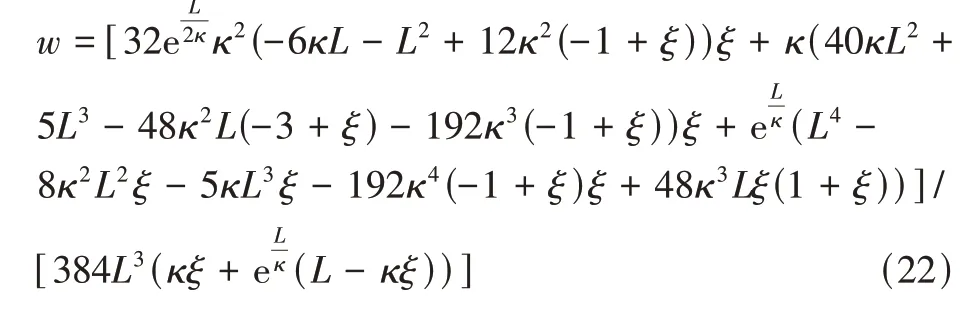
撓度曲線如圖2 所示。可以看出撓度隨著κ和ξ的增大而減小。

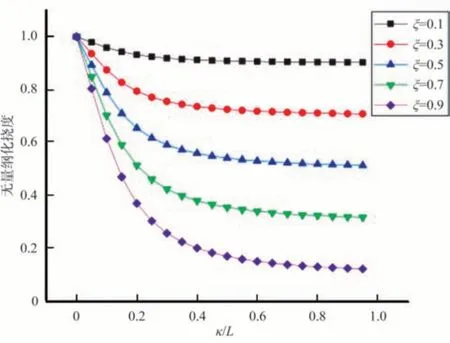
圖2 兩端固支受均勻載荷時撓度變化曲線Fig.2 The deflection curve of the fixed support at both ends under uniform load

同理可得其他邊界條件無量綱化撓度變化曲線，如圖3～圖7所示。也可以看出撓度隨著兩個非局部參數的增大而減小，可以獲得一致性的強化效應。

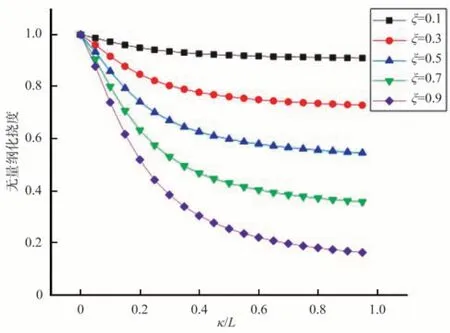
圖3 左端固支右端簡支受均勻載荷時撓度變化曲線Fig.3 The deflection curve of the left end fixed support and the right end simply supported under uniform load

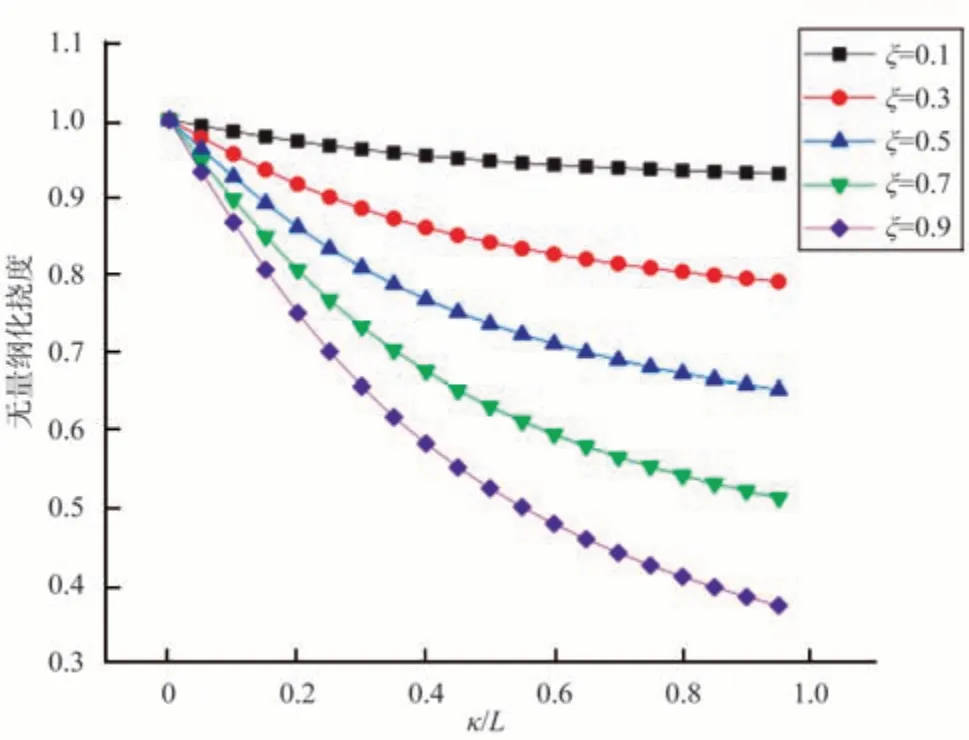
圖7 左端簡支右端導支,右端受到集中荷載時的撓度變化曲線Fig.7 The deflection curve when the left end is simply supported and the right end guide is subjecte to concentrated load

2.2 歐拉梁的屈曲

假定在歐拉梁的端部受到一個縱向的集中載荷，大小為Nt，那么外力功為

其中，Nt還可以表示為

其中，p為壓力。

根據哈密頓變分原理，同理可得控制方程

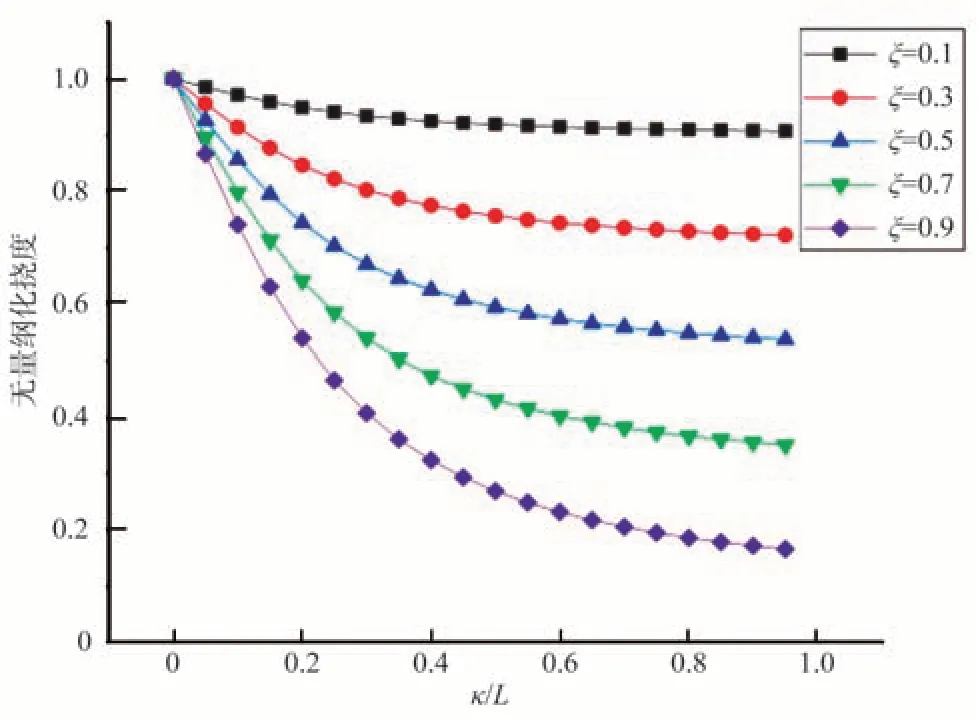
圖4 左端固支右端導支受均勻載荷時撓度變化曲線Fig.4 The deflection curve of the left-end fixed support and the right-end guide support under uniform load

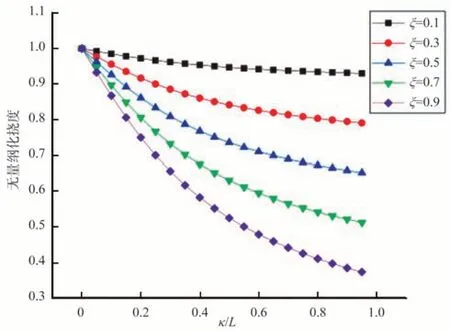
圖5 左端固支右端自由,右端受到集中荷載時的撓度變化曲線Fig.5 The deflection curve when the left end is fixed and the right end is free,and the right end is subjected to concentrated load

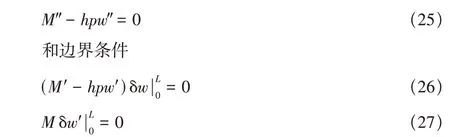
其中M和上述情況一樣均表示為

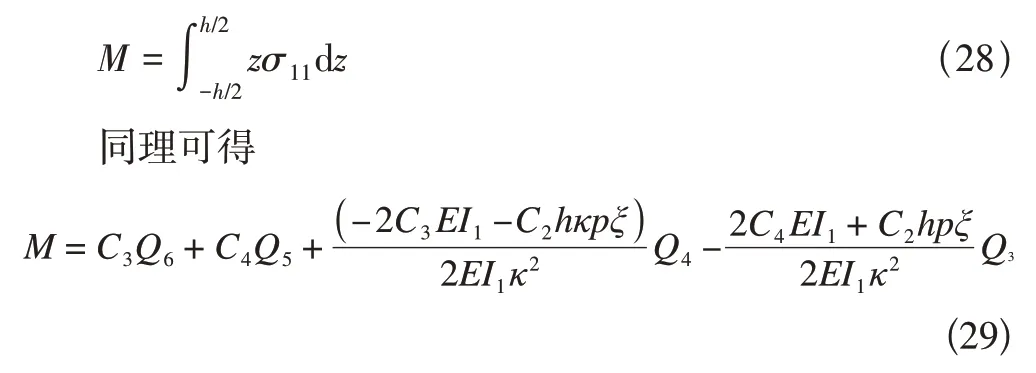
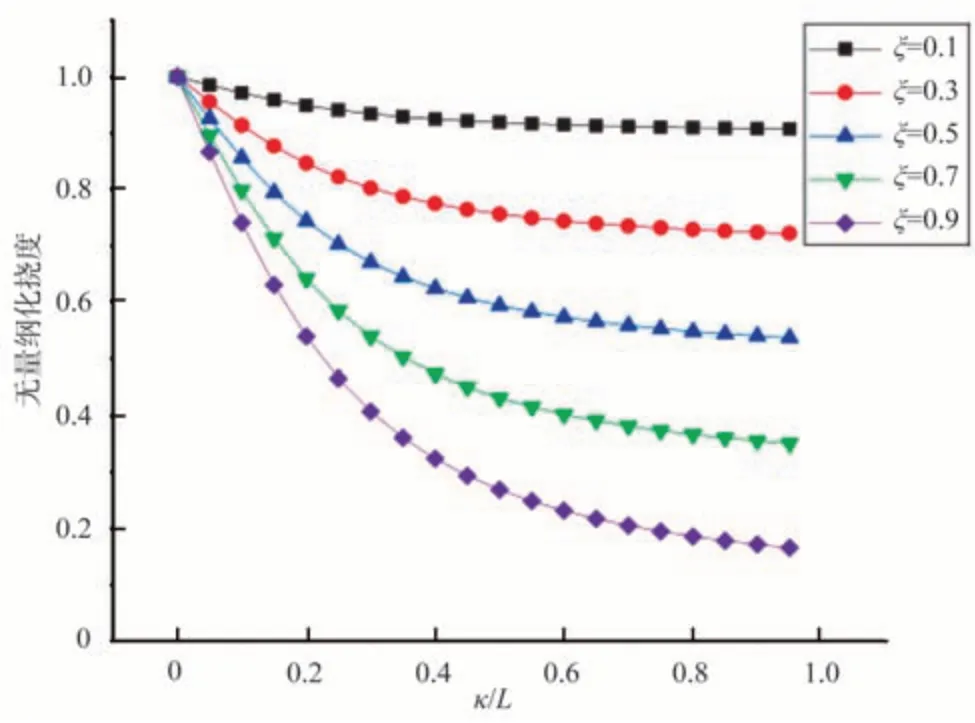
圖6 左端固支右端導支,右端受到集中載荷時的撓度變化曲線Fig.6 The deflection curve of the left end fixed support and the right end guide support when the right end is subjected to a concentrated load

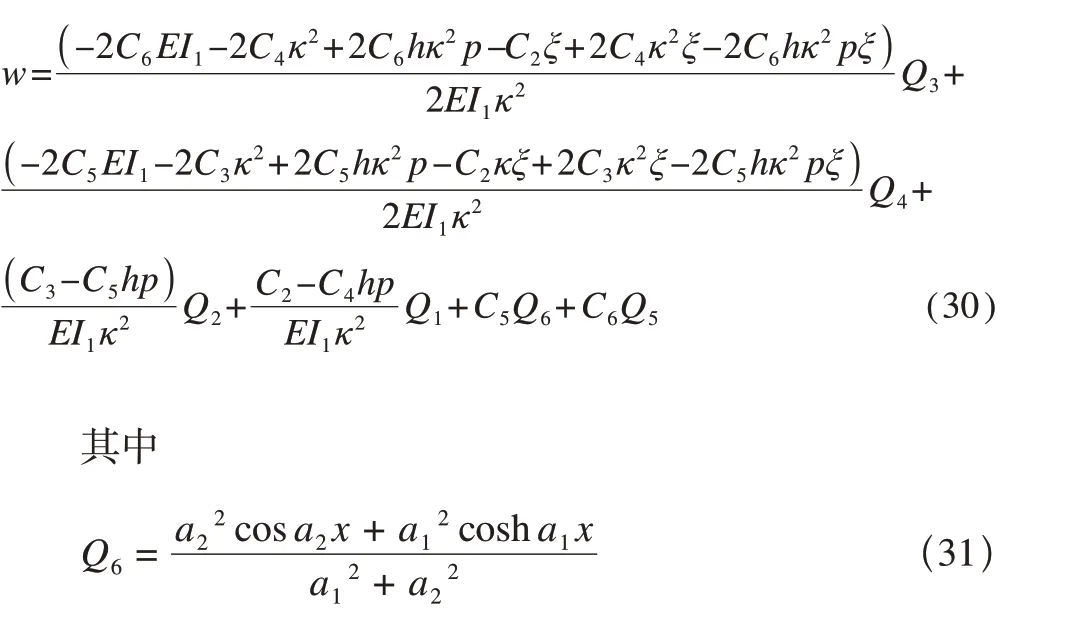
根據式（20）、式（26）、式（27）求出未知常量。對于不同的邊界條件，都可以得出5個未知常量中有兩個等于零，其余三個未知常量所在的剩余三個方程剛好聯立組成一個線性齊次方程組。對于線性齊次方程組，若存在非零解，則它的系數矩陣行列式等于零，以兩端固支的邊界條件為例，可以先得到邊界條件為

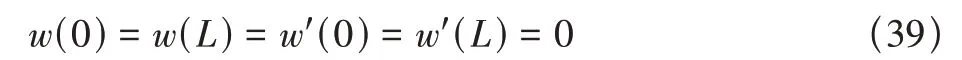
可以求解出C5=0 和C6=0，剩下的三個未知常量C2、C3、C4所在的剩余三個方程的系數矩陣行列式必須等于零，通過求解行列式等于零的方程，將得到的結果p進行無量綱化，得到歐拉梁兩端固支時的無量綱化的屈曲載荷變化曲線，如圖8所示。可以看出歐拉梁兩端固支時的無量綱化的屈曲載荷隨著兩個非局部參數κ和ξ的增大而增大。

圖8 兩端固支時的屈曲載荷變化曲線Fig.8 Dimensionless buckling load variation curve when both ends are clamped

同理可得，其他邊界條件也依次如圖9～圖13所示。均可以看出無量綱化的屈曲載荷隨著兩個非局部參數κ和ξ的增大而增大，可以獲得一致性的強化效應。

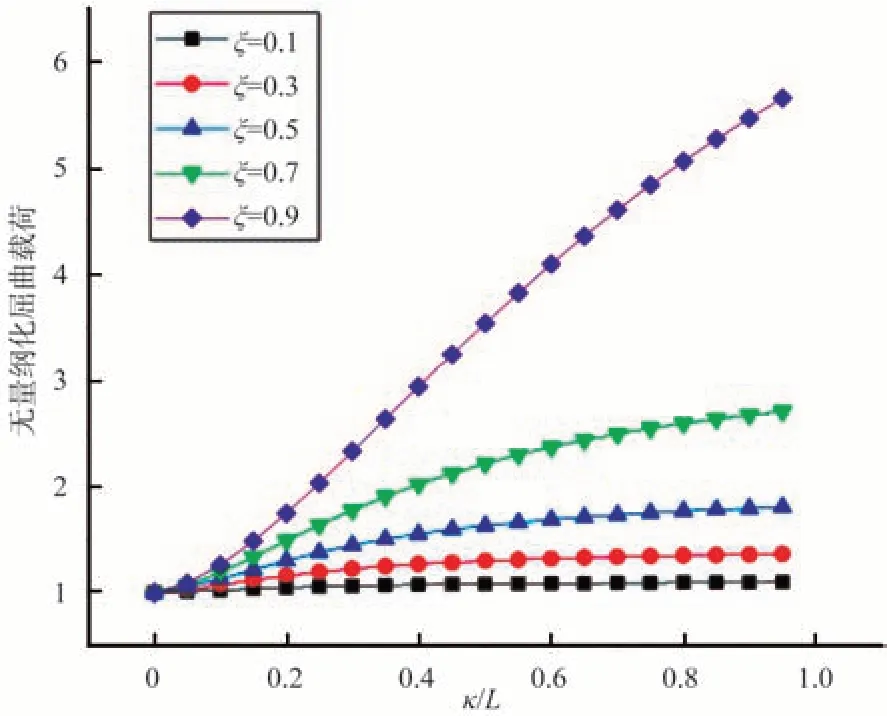
圖9 左端固支右端簡支時的屈曲載荷變化曲線Fig.9 Dimensionless buckling load variation curve when both ends are clamped

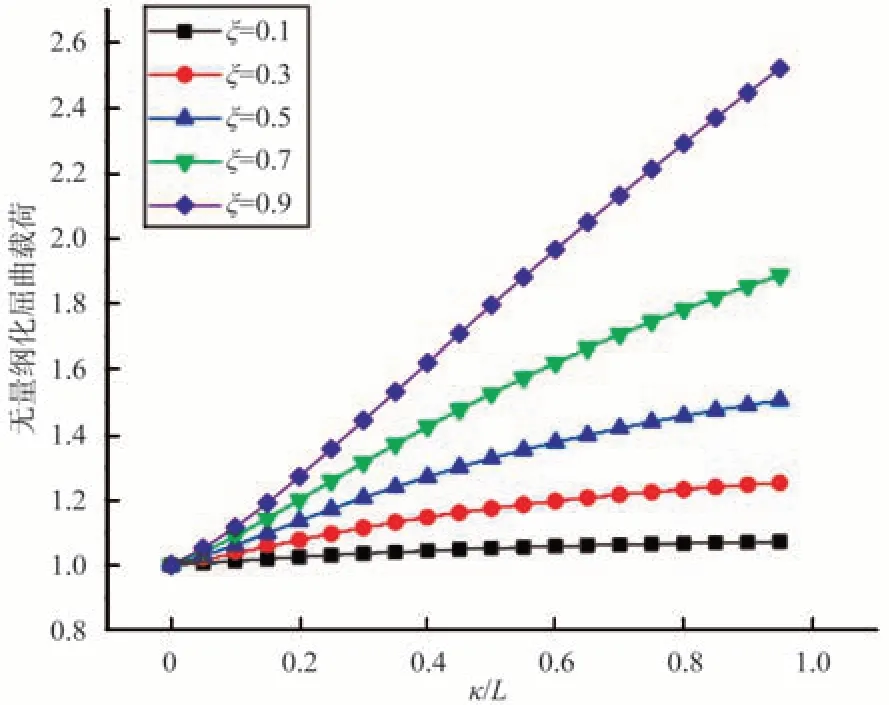
圖13 左端簡支右端導支時的屈曲載荷變化曲線Fig.13 Dimensionless buckling load variation curve when the left end is simply supported and the right end guide is supported

2.3 歐拉梁的自由振動

對于歐拉梁的自由振動，動能為

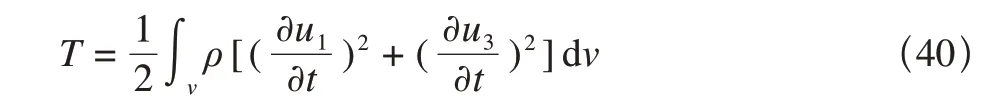
式中，ρ為密度。根據哈密頓變分原理，同理可得控制方程為

和邊界條件為

其中

其中，M和w可以表示為時間的諧波函數，即

代入控制方程可得

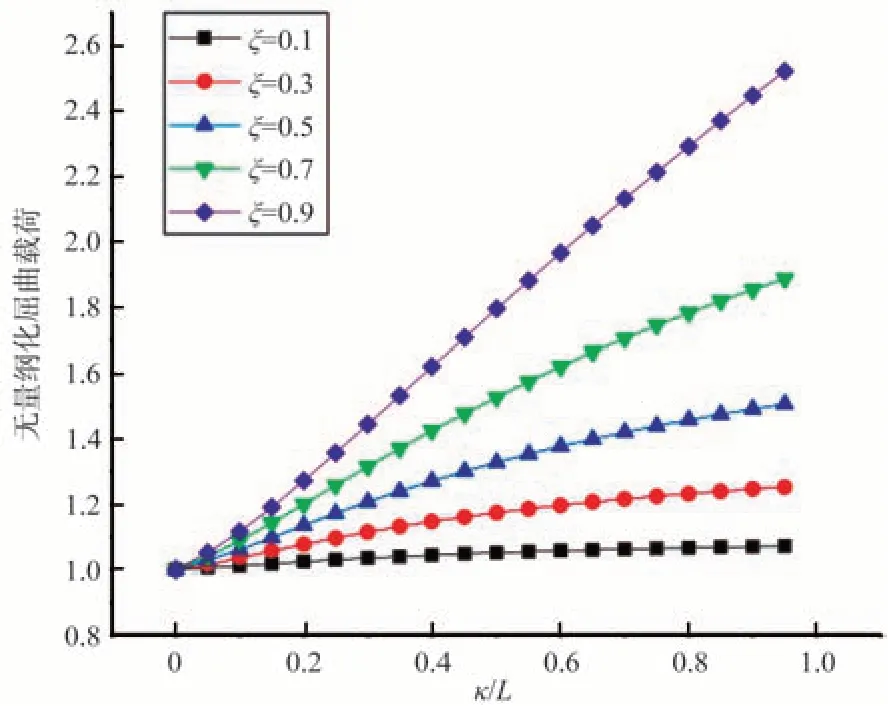
圖10 左端固支右端自由時的屈曲載荷變化曲線Fig.10 Dimensionless buckling load curve when the left end is fixed and the right end is free

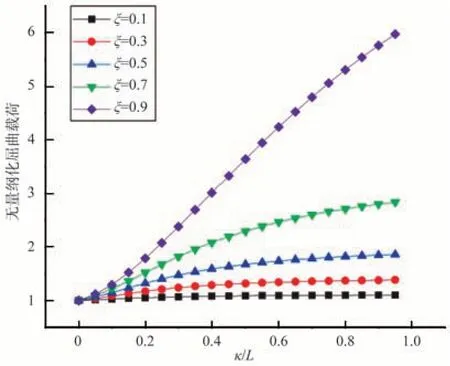
圖11 左端固支右端導支時的屈曲載荷變化曲線Fig.11 Dimensionless buckling load curve of the left-end fixed support and the right-end guide support

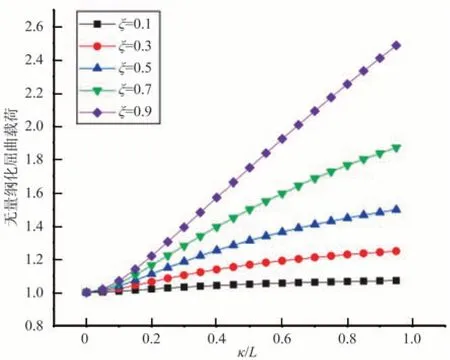
圖12 兩端簡支時的屈曲載荷變化曲線Fig.12 Dimensionless buckling load variation curve when both ends are simply supported

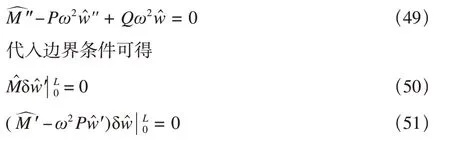
同理可得

此類問題和上述屈曲一樣，也是一個求解線性齊次方程組的問題，以兩端固支邊界條件為例，得到的歐拉梁兩端固支時的無量綱化的振動頻率變化，如圖14所示。可以看出無量綱化振動頻率隨著兩個非局部參數κ和ξ的增大而增大。同理可得，其他邊界條件情況如圖15～圖19 所示。也都反映出無量綱化振動頻率隨著兩個非局部參數κ和ξ的增大而增大，可以獲得一致性的強化效應。

圖14 兩端固支時的振動頻率變化曲線Fig.14 Dimensionless vibration frequency change curve when both ends are clamped

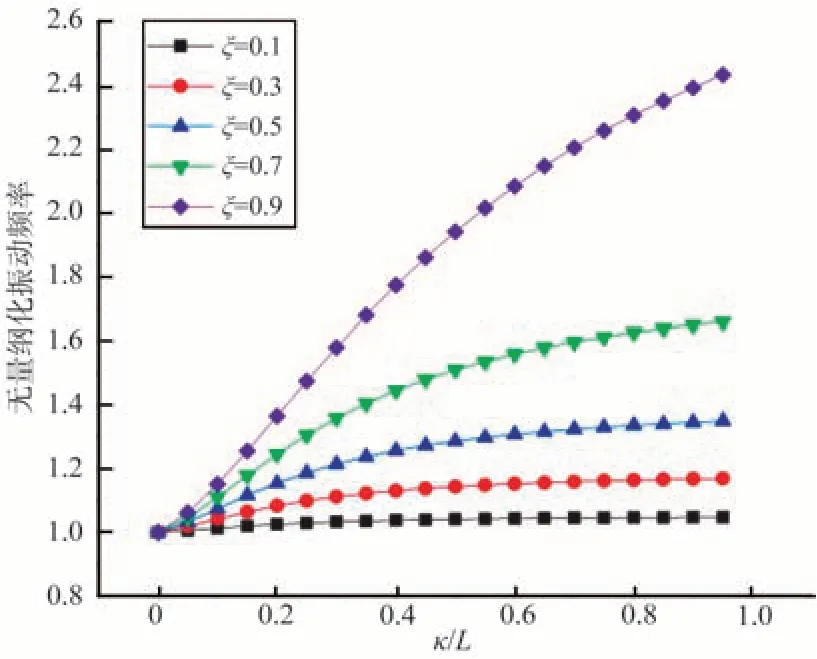
圖15 左端固支右端簡支時的振動頻率變化曲線Fig.15 Dimensionless vibration frequency curve when the left end is fixed and the right end is simply supported

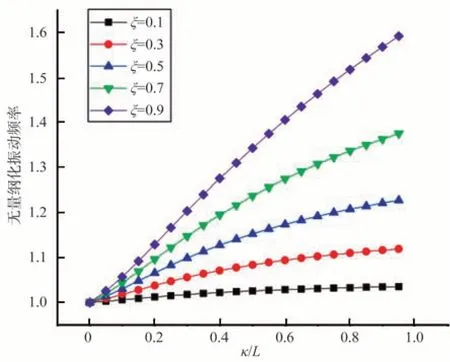
圖19 左端簡支右端導支時的振動頻率變化曲線Fig.19 Dimensionless vibration frequency change curve when the left end is simply supported and the right end guide is supported

3 結論

本文基于應力驅動的非局部積分模型，從理論上研究了非局部效應對歐拉-伯努利梁力學特性的影響。本構關系是第一類Fredholm型積分方程，通過簡單調整積分極限，轉化為第一類Volterra 積分方程。通過拉普拉斯變換和積分本構關系相關的邊界條件和額外約束方程確定最終解，對于屈曲和自由振動，為了獲得唯一的解，通過求線性齊次方程組的非零解，得到屈曲載荷和自由振動頻率，并將其無量綱化。在各種邊界條件下，可以觀察到與尺寸相關且一致的增韌效應，即不同邊界條件下，隨著非局部參數的增大，撓度減小，而屈曲載荷和振動頻率增大。得到微尺度歐拉梁的彎曲、屈曲、自由振動的變化規律將有利于MEMS航空壓力傳感器的結構設計與優化，提高測量精度，還可以運用于各個微系統領域，支持微尺度梁的結構力學特性研究。

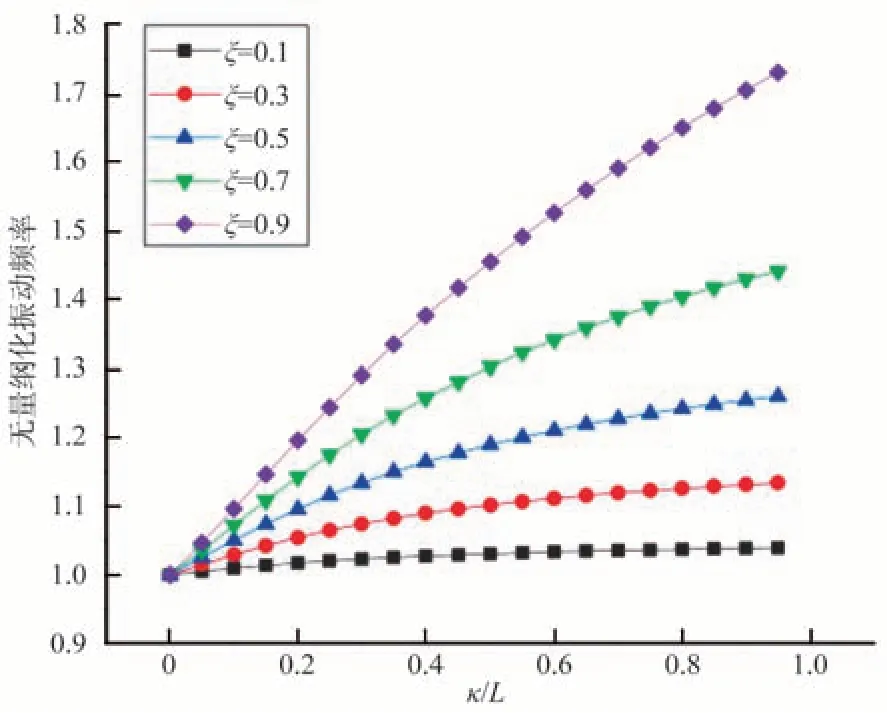
圖16 左端固支右端自由時的振動頻率變化曲線Fig.16 Dimensionless vibration frequency curve when the left end is fixed and the right end is free

圖17 左端固支右端導支時的振動頻率變化曲線Fig.17 Dimensionless vibration frequency curve of the left end fixed support and the right end guided support

圖18 兩端簡支時的振動頻率變化曲線Fig.18 Dimensionless vibration frequency variation curve when both ends are simply supported